雙模式外骨骼結構設計與優化

馮軍， 王衛辰， 劉興實， 文天陽， 張冰玉， 黃琪

（江蘇師范大學a.江蘇圣理工學院-中俄學院；b.機電工程學院，江蘇 徐州221116）

0 引 言

機械外骨骼是一種由金屬框架構成的可以提供額外能量以供肢體運動的輔助設備。國外外骨骼的研究始于20世紀60年代，用于增強士兵的舉重和攜帶能力[1]。隨著科技水平的進步，2000年以后研究設計了一大批外骨骼系統，以軍用、醫療輔助、助力行走等領域為主。軍用機械外骨骼主要用于提高士兵的單兵作戰能力；醫療機械外骨骼可以幫助行動能力下降和神經受損的病人進行康復訓練；民用機械外骨骼主要用于行動不便的老人和殘疾人，為其提供輔助行走能力[2]。國內下肢外骨骼多以學術研究為主，2005年前后，國內多家科研院所開展了下肢外骨骼方面的研究，其中具有代表性的有中科院合肥智能機械所、中科院常州先進制造技術研究所、浙江大學、哈爾濱工業大學、電子科技大學等[3]。在工業應用中，鐵甲鋼拳團隊開發的CEXO-01專用于物流行業[4]，該產品重約28 kg，可以讓普通工人便于背負重達60 kg的物品，滿電后可持續運行約4 h。應用壓力傳感器、無線傳導、陀螺儀等技術和儀器，幫助工人減輕負擔，減少身體傷害，并大大提高工作效率。為了兼具外骨骼結構的上述優點，同時達到功能多樣化的目的，本文設計雙模式外骨骼模型，將人體所受力的一部分轉移到外骨骼上，以幫助佩戴者降低勞動強度，優化受力部位，提高人體的負重能力。本文首先針對外骨骼的下肢座椅模式和上肢托舉模式進行結構設計及有限元分析，然后根據外骨骼的應力和位移分布狀況，對整體結構進行優化，期望在滿足功能和強度要求的前提下，盡可能減輕外骨骼結構的整體質量。

1 外骨骼模型的結構設計

根據GB 10000-1988《中國成年人人體尺寸》中的數據，取身高為1754 mm、體重為71 kg的人為例，設計外骨骼的結構尺寸。取大腿桿的長度為496 mm，小腿加足高的長度為439 mm。由于人體踝關節距足底的高度并不相同，設計了小腿桿桿長可調節的踝關節結構，其各部件的結構形式和裝配關系如圖1所示。踝關節調節部位設置牽引軌道，小腿桿連接零件在牽引軌道中定位，實現髖關節高度的調節。小腿桿在連接零件的不同深度固定，實現小腿桿桿長的調節。

通過對人體生理結構與工作模式的分析，初步設計出外骨骼結構模型。外骨骼結構總體由腳支撐結構、踝關節結構、小腿桿結構、膝關節結構、大腿桿結構、齒輪定位結構、萬向聯軸器結構、髖關節結構等組成，如圖2（a）所示。在外骨骼大腿桿中后部設置萬向聯軸器結構，在其轉換到上肢托舉工作模式后，可以滿足隨人體上肢左右擺動的情況，結構如圖2（b）所示。齒輪定位機構由齒輪、齒條、插齒結構、支撐軸及雙頭螺栓等零件組成，結構如圖2（c）所示。支撐軸繞小腿桿轉動，齒輪繞支撐軸上端的雙頭螺栓轉動，并與齒條相互嚙合。沿著支撐軸的軸線方向，手動控制插齒結構的前后移動，插齒可使齒輪停止轉動，與支撐軸、大腿桿、小腿桿相互限制，以滿足座椅模式的工作狀態。

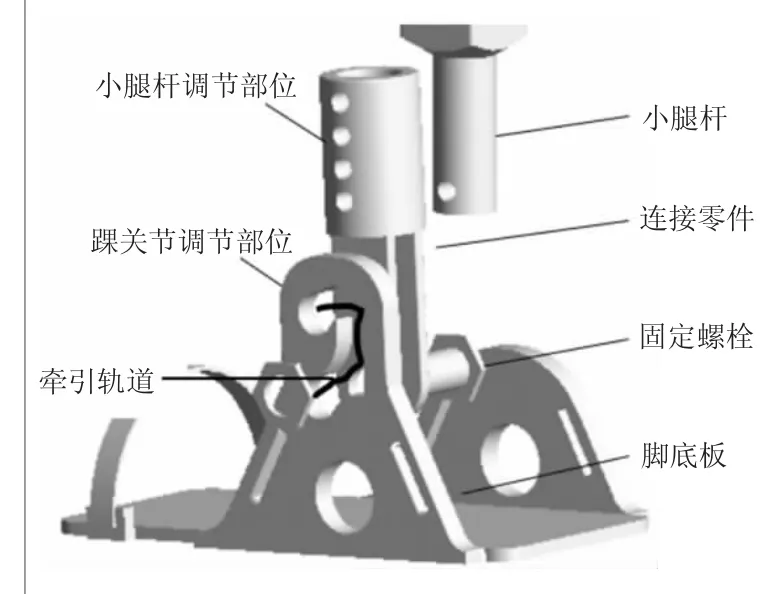
圖1 小腿桿桿長可調節的踝關節結構

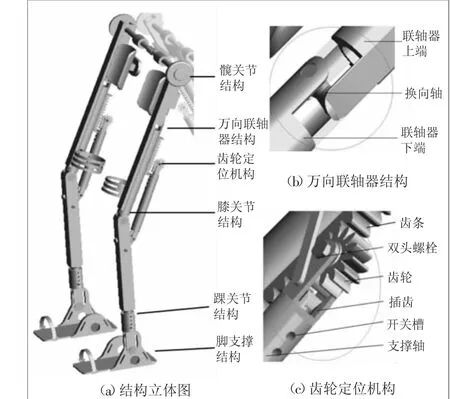
圖2 外骨骼外觀結構立體圖及細節圖

2 外骨骼座椅模式和托舉模式分析

2.1 外骨骼座椅模式分析

外骨骼座椅可以使佩戴者積極地調動肌肉的力量,而不是被動地坐著，有利于提高勞動持久性。考慮到穿戴者座椅位姿的不同，即膝關節的彎曲程度不同，以及為轉換到上肢托舉做適應性調整，在膝關節部位追加制動結構，使其具有座椅功能。綜合考慮應用齒輪齒條嚙合，配合插齒等配套制動結構，滿足外骨骼支撐條件，如圖2（c）齒輪定位機構所示。齒輪齒條不同的嚙合位置滿足不同的位姿需求，通過手動操作使插齒與齒輪嚙合，從而固定齒輪齒條，起到制動器的目的，實現座椅功能。齒輪定位機構的角度變換示意圖如圖3所示。

為了方便網格劃分、減少計算工作量，對實體座椅模型做如下簡化[5]：除去腰部動力裝置和各連接綁帶，髖關節部位用連桿代替；略去各關節的驅動裝置；可調桿件上的螺栓與孔也被簡化，以便施加載荷。對外骨骼進行有限元分析的基本步驟為[6]：

1）定義材料屬性為6061A鋁合金，設置密度為2700 kg/m3。

2）在Pro/E中建立模型并導入ANSYS中。

3）采用整體網格對各個零部件進行網格劃分，網格精度為0.01m。

4）施加約束和載荷。腳底板是與地面相接觸的部分，腳底板及踝關節采用全約束，所有的關節都鎖死不會發生相對運動，外骨骼所承受的質量約為80 kg，即在模型中加載784 N垂直向下的均布載荷。

5）使用Von-Mises靜態分析算法分析外骨骼位移變化和應力變化，得到位移云圖、應力云圖，如圖4所示。

由圖4可以看出外骨骼不同部位所受應力與位移情況，以及不同部位應力與位移的變化趨勢。由圖4（a）可知，在該位姿下，外骨骼大腿上端位移量最大，且位移量隨肢體高度呈規律性遞增。由圖4（b）可知，在踝關節和小腿中上部的應力最大。為了得到相同載荷作用下不同位姿狀態的應力和位移變化，在Pro/E中，重新調整膝關節的約束狀態，改變膝關節的角度，再導入到ANSYS中重復前述步驟進行分析，將結果整合到一個示意圖中，如圖5所示。

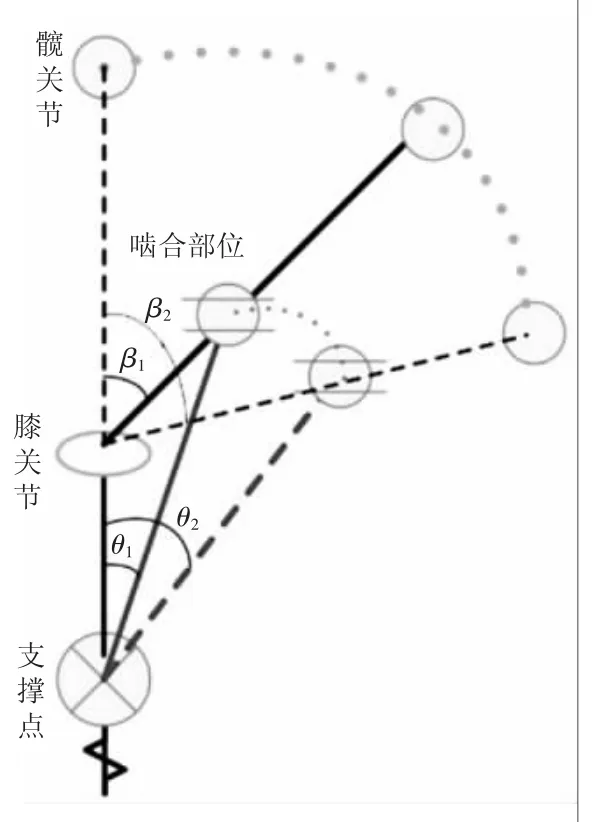
圖3 齒輪定位機構的角度變換示意圖

圖4 外骨骼座椅模式有限元分析結果

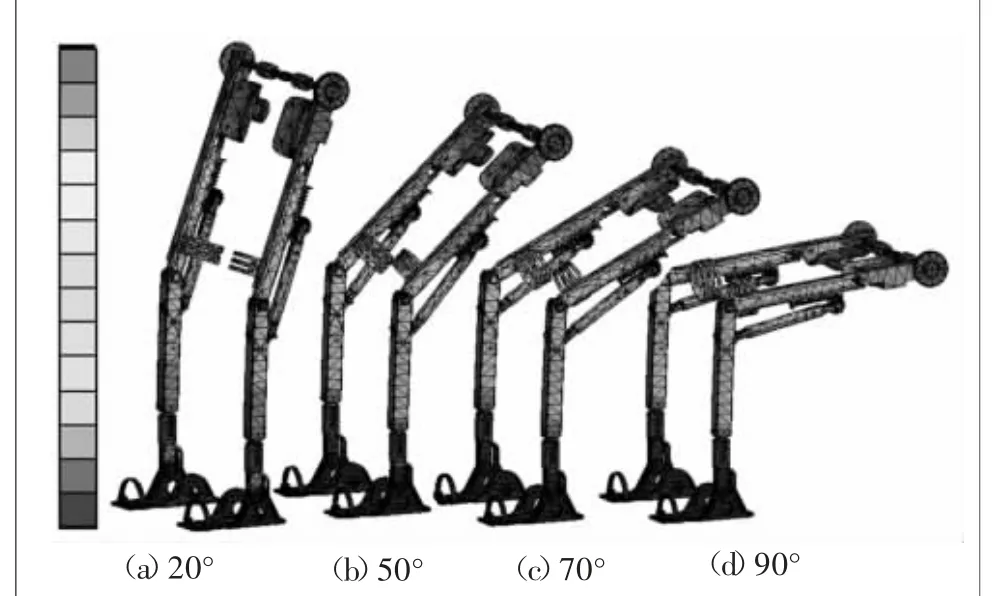
圖5 不同位姿下外骨骼位移變化示意圖

從圖5中可看出，在相同載荷、不同位姿下，同一部位的變形量并不相等，最大變形量都在大腿上端，且隨著角度的增加，最大變形量的區域呈遞減趨勢；最小變形量都在腳底板附近，變化規律大體一致，但是變化幅度不同。由于最小二乘法得到的數值結果，在不使用任何降噪處理的情況下，是光滑和準確的[7]。為了清晰地表達不同位姿下位移、應力的具體變化，用最小二乘法分別擬合這4種位姿下的位移、應力的最大值和平均值。由于三階及以上多項式的和方差（SSE）接近0，擬合優度（R-square）為1[8]，均能夠滿足擬合要求，所以采用準確性較高、階次較低的三階多項式函數進行擬合，其通式為

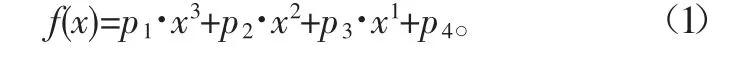
式中：pi表示多項式的擬合系數；xi表示膝關節的角度；f(x)表示位移變化量或應力變化量。

求得三階多項式的系數及和方差（SSE）、擬合優度（R-square）如表1所示，位移變化量隨膝關節角度的變化如圖6所示，應力變化量隨膝關節角度的變化如圖7所示。

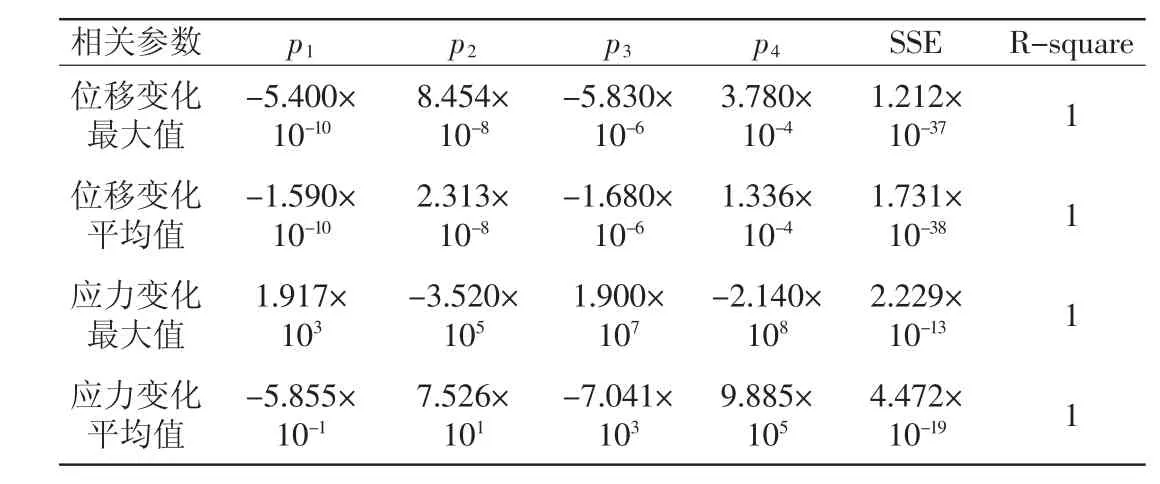
表1 座椅模式下多項式的系數及誤差結果表

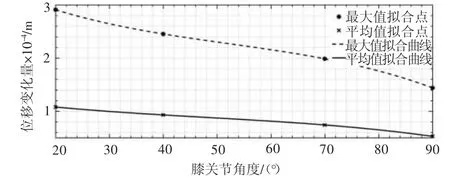
圖6 位移變化量隨膝關節角度變化的擬合曲線

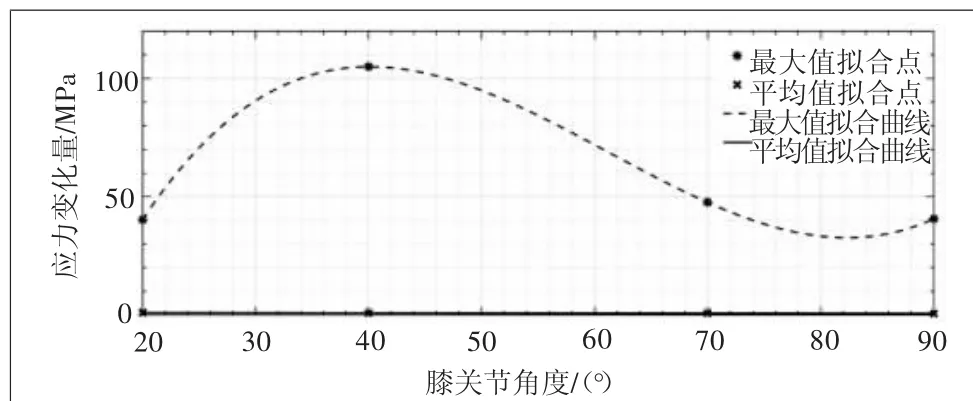
圖7 應力變化量隨膝關節角度變化的擬合曲線

從擬合圖中可以分析得出，隨著膝關節角度（與豎直方向的夾角）的增加，外骨骼的最大變形量總體在減少，呈負相關；而外骨骼的最大應力先增加再減少。由以上分析可知，在膝關節角度為40°附近，最大應力出現在小腿支架上的支撐點結構區域，為104 MPa，較為接近材料屈服強度110 MPa，所以該處應視為潛在的危險部位，需對其進行針對性強化。

2.2 上肢托舉模式分析

由于上肢與下肢在結構和運動軌跡上具有一定的相似性，所以在特定的約束范圍內，該裝置也可實現上肢托舉模式，完成托舉任務[9]。在對原結構盡可能少改動的情況下，在其髖關節處追加限位結構；在膝關節和髖關節之間增加萬向聯軸器結構，增加托舉時的肢體跟隨自由度；踝關節（如圖1）處連接結構解除固定件后，可從定位槽中拔出，減輕外骨骼的質量和消除腳底污垢的影響；再配合相應綁帶的固定約束，使上肢更加貼合外骨骼。上肢托舉模式的工作示意圖如圖8所示，圖中θ為桿1與水平方向的夾角，β為桿2 與水平方向的夾角。

將轉化為上肢托舉模式的外骨骼模型導入到ANSYS中進行有限元分析，根據成年人體重在上肢部位的比例，確定作用在外骨骼上的載荷約為196 N，對其進行精度為0.01 m的網格劃分，在髖關節施加全約束，在與上肢大臂接觸的外骨骼部位施加均布載荷，然后重復外骨骼座椅工作模式的分析步驟，得到如圖9所示的位移云圖、應力云圖。

從圖9（a）中可見，最大變形量發生在上肢前端，離髖關節部位越遠外骨骼的變形量越大。從圖9（b）中可見，在萬向聯軸器和制動連接部位的應力最大。為了清晰地表達不同位姿下位移、應力的具體變化，在θ角分別為1°、30°、60°和90°的狀態下，用最小二乘法分別擬合這4種位姿下該處位移、應力的最大值和平均值。同樣采用三階多項式進行擬合，其系數及SSE、R-square如表2所示。不同幅度下位移、應力的最大值和平均值擬合曲線如圖10、圖11所示。

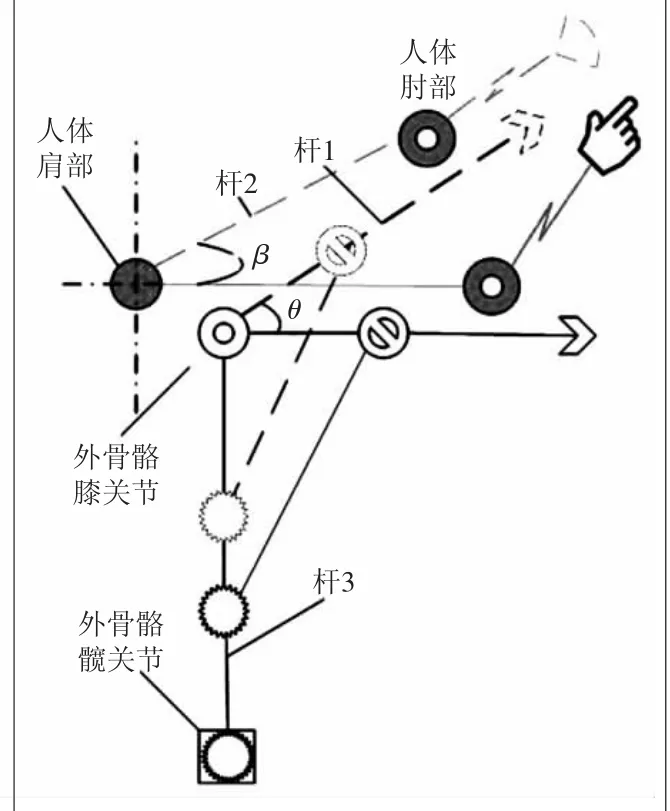
圖8 上肢托舉模式工作示意圖

圖9 外骨骼上肢托舉模式有限元分析結果

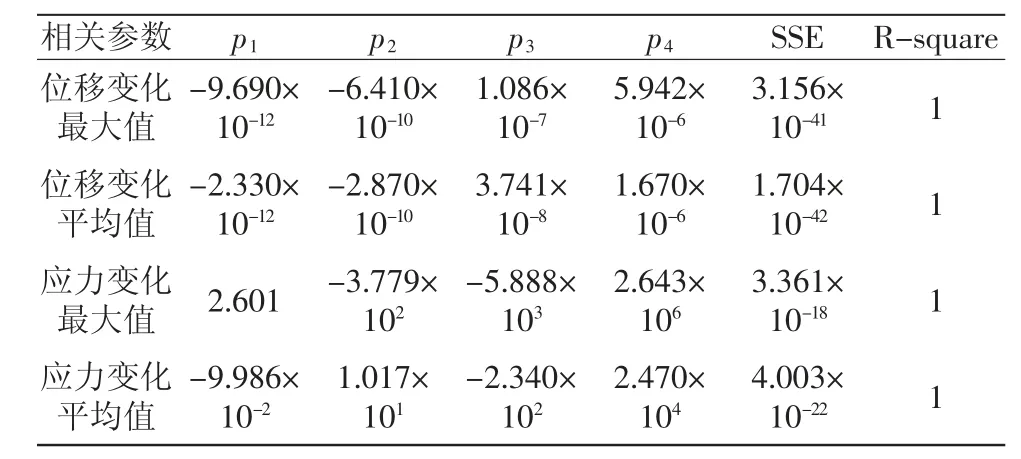
表2 托舉模式下多項式的系數及誤差結果表

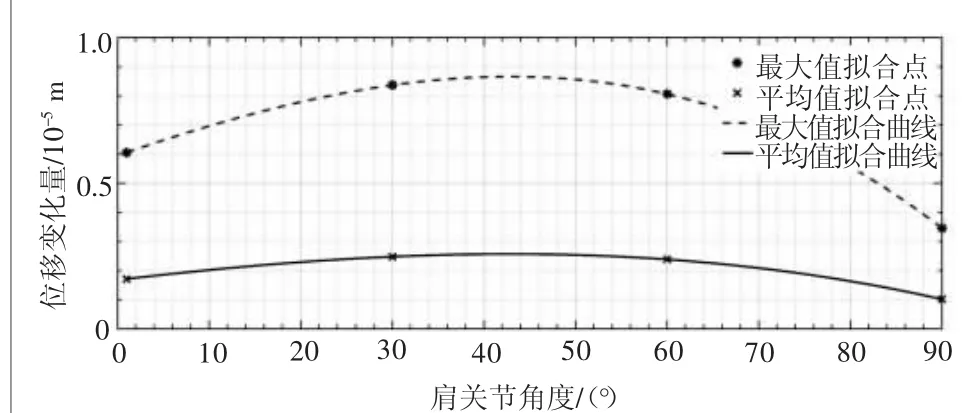
圖10 位移變化量隨肩關節角度變化的擬合曲線

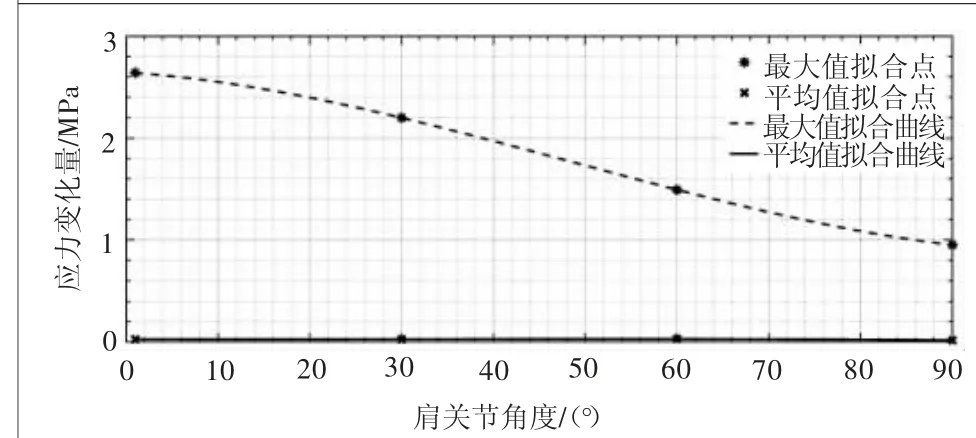
圖11 應力變化量隨肩關節角度變化的擬合曲線

由圖10和圖11可以看出，隨著β角的增加，外骨骼的最大變形量總體先增加再減少，且在肩關節角度為45°附近有最大變形；而外骨骼的最大應力總體呈遞減趨勢，為負相關，最大應力出現在手臂接近水平狀態時，此時手臂的力完全作用于支架，約為2.64 MPa，遠低于材料的屈服強度。由圖6～圖7、圖10～圖11中可知，最大值與平均值相差較大，說明外骨骼整體結構的受力不均勻，力在各部件之間的傳遞不夠均勻，可通過在應力最大處加固材料或增大接觸面積等措施提高裝置的承載力。

2.3 外骨骼模式的轉換過程分析

從座椅模式轉換到上肢托舉模式的過程中，考慮到人體大腿部位與軀干部位的長度接近，下肢與上肢的長度接近，結合關節角的變化幅度，髖關節部位逆時針轉動180°實現模式的轉換。轉換后外骨骼在卡位裝置的固定下，髖關節到萬向聯軸器之間的部位保持豎直狀態，萬向聯軸器可實現擺動，使外骨骼隨實際托舉姿勢的變化而變化。限位裝置安裝在髖關節部位的轉動軸上，將髖關節轉動的角度范圍限制在-90°～+180°之間，外骨骼站立時為0°。圖12所示為轉換過程示意圖，其中角度以逆時針旋轉為正、順時針為負。

通過上述分析可知，座椅模式承受人體的總重力，而托舉模式只承受上肢的重力，兩種工作模式的受力大小不同,受力部位也不同。座椅模式的受力部位在裝置的大腿部位，腳底板的狀態為全約束，即外骨骼受到的力傳遞到地面；托舉模式的受力部位在裝置的小腿桿部位，髖關節的狀態為全約束，即外骨骼的受力傳遞到人體腰背部。對于長時間利用上肢或下肢從事重復性操作的勞動者，這種可轉換工作模式的外骨骼能夠有效緩解勞動強度，改善人體受力部位，提高工作效率。

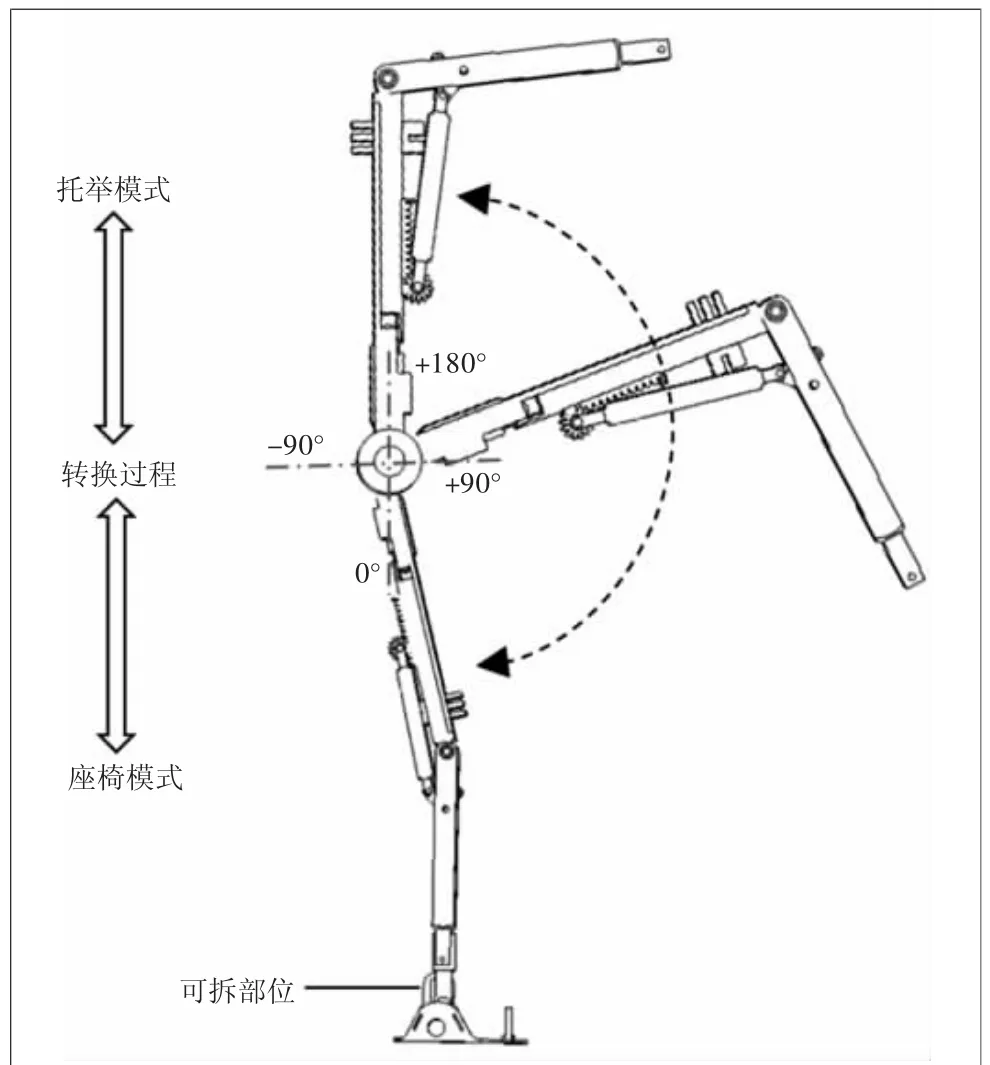
圖12 模式轉換過程示意圖

3 外骨骼的結構優化

前述的分析設計側重于模型的結構、尺寸和薄弱部位的確定，并未考慮外骨骼的質量，整個裝置的質量有可能沒有達到最優分布狀態。為了便于使用者長期佩戴，故有必要進一步對裝置進行拓撲優化，以降低外骨骼的質量。拓撲優化的主要思想是將尋求結構的最優拓撲問題轉化為在給定的設計區域內尋求最優的材料分布問題，最終得到最佳的材料分配方案[10]。以座椅模式為例，將初步設計好的外骨骼模型，按照前述工作模式的步驟定義材料屬性，施加均布載荷和約束狀態，對整體進行精度為0.01m的網格劃分，用Shape Optimization(Beta)工具進行拓撲優化，設定最大目標削減量為25%，得到如圖13所示的外骨骼拓撲優化立體圖，操作的相關參數如表3所示。

圖13 外骨骼拓撲優化立體圖及細節圖

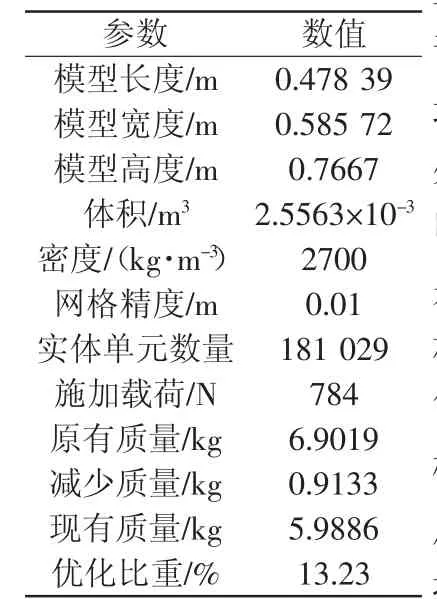
表3 外骨骼拓撲優化相關參數表

由圖13和表3可知，外骨骼的整體結構變化不大，減重最大的部位為髖關節部位，與前文所述最大變形量處相對應。經過優化處理，裝置質量減少了13.23%。明顯得到優化的區域從上到下分別為：1）上端髖關節部位。在滿足材料強度的前提下，裝配接口需簡化。2）大腿部位。支撐桿件需開槽處理，萬向聯軸器加固部位采用單邊加固，在小腿支架上的支撐點結構部位增加壁厚或增加支撐軸數量等。3）支撐固定環部位。進行柔性處理，支撐板部分用彈性軟墊代替，增加綁帶約束。4）腳底板部位。綁帶固定槽的位置降低高度。

根據外骨骼優化結果，在Pro/E中對模型進行修改，然后求出4處位姿下位移變化量與應力變化量的最大值及平均值，用最小二乘法進行擬合，將優化前后位移與應力的最大值與平均值進行對比，分別如圖14、圖15所示。通過圖14可知，優化后位移變化量的最大值與平均值都相應小幅度變大，最大值的整體增大幅度高于平均值，與裝置質量大幅度減少、位移變化量小幅度增大相對應，同時也證明了外骨骼優化的效果較明顯；由圖15可知，優化后的應力變化量的平均值變化幅度不明顯，最大值變動幅度趨于平穩，說明外骨骼所受的應力受膝關節角度變化的影響降低，有利于外骨骼在不同位姿下安全與平穩地工作，表明外骨骼優化模型的有效性。

4 結 論

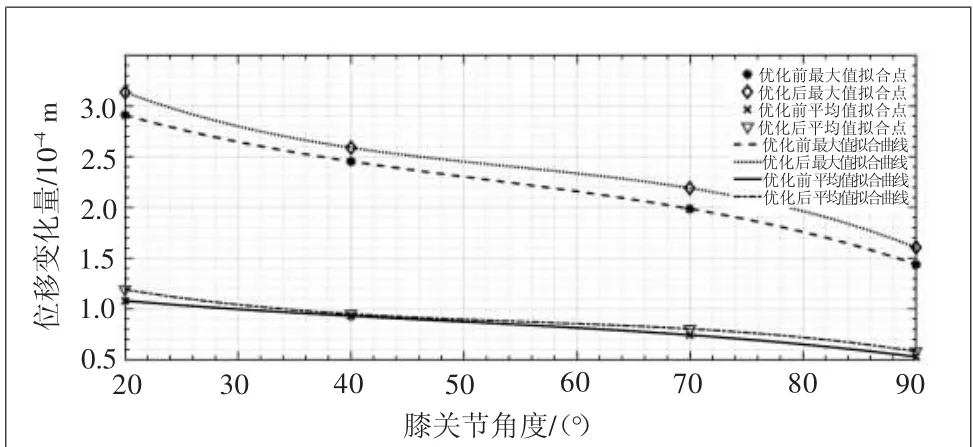
圖14 位移變化量優化前后對比結果

圖15 應力變化量優化前后對比結果

可穿戴式的機械外骨骼能夠在很大程度上提高人體能量的利用率，包括力量、耐力等，不論是在軍事領域還是民用方面都有較大的應用前景。本文采用膝關節部位提供緩沖制動的方案，建立了能夠適應座椅和上肢托舉兩種工作模式的外骨骼模型，并利用ANSYS Workbench分析了模型結構的可行性，最后對外骨骼進行了拓撲優化，使其質量更輕，減輕人體負荷。本文研究和設計的雙模式外骨骼結構，可應用于下肢助力行走和上肢助力托舉，為外骨骼的多模式設計與應用提供了參考。