遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)在電液力伺服系統(tǒng)辨識(shí)中的應(yīng)用

周挺， 王虎

（航空工業(yè)飛機(jī)強(qiáng)度研究所，西安710065）

0 引 言

電液力伺服系統(tǒng)結(jié)合了電子技術(shù)、伺服控制、液壓傳動(dòng)和傳感器技術(shù)，通過(guò)電液信號(hào)轉(zhuǎn)換實(shí)現(xiàn)被控對(duì)象力控加載，具有功率質(zhì)量比大、結(jié)構(gòu)緊湊、響應(yīng)快、系統(tǒng)剛度大、控制精度高的特點(diǎn)，廣泛應(yīng)用于飛機(jī)結(jié)構(gòu)強(qiáng)度試驗(yàn)中。由于伺服閥的死區(qū)和游隙、油溫和油壓的變化、黏性摩擦力等影響，系統(tǒng)為參數(shù)時(shí)變、非線性系統(tǒng)[1-2]。建立系統(tǒng)精確數(shù)學(xué)模型可為控制系統(tǒng)的分析和設(shè)計(jì)提供有力依據(jù)[3]，基本建立方法包括機(jī)理建模法和系統(tǒng)辨識(shí)建模，機(jī)理建模需要對(duì)系統(tǒng)做一些合理假設(shè)，通過(guò)確切的數(shù)學(xué)表達(dá)式描述系統(tǒng)的內(nèi)部機(jī)理，系統(tǒng)辨識(shí)建模則是在輸入和輸出數(shù)據(jù)的基礎(chǔ)上，從給定的模型類(lèi)中確定一個(gè)具有與辨識(shí)系統(tǒng)輸入輸出特征相同的等價(jià)模型。多層前饋BP（Back-Propagation）神經(jīng)網(wǎng)絡(luò)作為一種反向傳播學(xué)習(xí)的非線性網(wǎng)絡(luò)，具有良好的非線性映射能力、自適應(yīng)能力、并行處理和全局優(yōu)化能力，能有效辨識(shí)多輸入多輸出的復(fù)雜非線性系統(tǒng)[4]，但存在收斂速度較慢、對(duì)初始權(quán)值敏感、容易收斂至局部極小等缺點(diǎn)。遺傳算法（Genetic Algorithm）是一種基于自然選擇優(yōu)勝劣汰和群體遺傳演化的自適應(yīng)概率搜索算法[5]，具有很強(qiáng)的魯棒性、并行計(jì)算能力和全局搜索能力。

本文采用遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)對(duì)電液力伺服系統(tǒng)進(jìn)行系統(tǒng)辨識(shí)建模，通過(guò)遺傳算法和BP算法的混合優(yōu)化，獲得最佳的網(wǎng)絡(luò)權(quán)值和閾值參數(shù)；將該辨識(shí)模型與線性參數(shù)模型的辨識(shí)結(jié)果進(jìn)行比較，驗(yàn)證遺傳優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)在系統(tǒng)辨識(shí)建模上的有效性。

1 電液力伺服系統(tǒng)

電液力伺服系統(tǒng)結(jié)構(gòu)如圖1所示，控制器根據(jù)載荷傳感器反饋值和上位機(jī)指令值之差輸出閉環(huán)控制信號(hào)，伺服驅(qū)動(dòng)器實(shí)現(xiàn)閉環(huán)控制信號(hào)放大和轉(zhuǎn)換，電液伺服閥根據(jù)驅(qū)動(dòng)信號(hào)轉(zhuǎn)換為對(duì)應(yīng)液壓負(fù)載流量，改變非對(duì)稱(chēng)液壓缸活塞位移，將載荷施加至負(fù)載（試驗(yàn)件）。首先建立電液伺服系統(tǒng)數(shù)學(xué)模型，可為系統(tǒng)辨識(shí)建模提供理論依據(jù)。

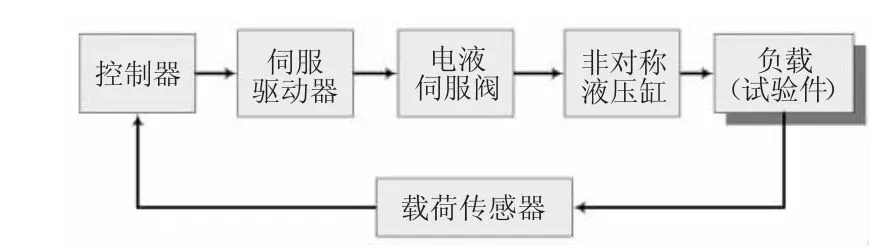
圖1 電液力伺服系統(tǒng)結(jié)構(gòu)圖

伺服驅(qū)動(dòng)器和載荷傳感器作為信號(hào)轉(zhuǎn)換模塊，其轉(zhuǎn)角頻率較系統(tǒng)固有頻率很高，可視為比例環(huán)節(jié)，其增益分別為Kd和Kf。

電液伺服閥由力矩馬達(dá)和液壓放大器組成[6]，第一級(jí)為雙噴嘴擋板，第二級(jí)為四通滑閥，其動(dòng)力學(xué)模型多采用二階振蕩環(huán)節(jié)形式，伺服閥空載流量qL0（s）滿(mǎn)足：

式中：kq為伺服閥流量增益；kc為伺服閥流量壓力增益；pL為負(fù)載壓力。kq和kc值隨閥工作點(diǎn)的變化而變化，由于閥經(jīng)常在零位工作，此處閥的流量增益kq0最大，流量壓力增益kc0最小，在系統(tǒng)分析時(shí)通常以零位系數(shù)作為閥的性能參數(shù)，kc0由伺服閥零位泄漏流量qc決定，kc0=qc/ΔpN,其中qc為伺服閥零位泄漏流量，ΔpN為額定壓降。

考慮液壓缸的內(nèi)泄漏、外泄漏和壓縮性流量，其流量連續(xù)性方程為

式中：A1為無(wú)桿腔活塞面積；A2為有桿腔活塞面積；xp為活塞位移；Ctp為液壓缸總泄漏系數(shù)，Ctp=（Cec/2+Cic）；Cec為液壓缸外泄漏系數(shù)；Cic為液壓缸內(nèi)泄漏系數(shù)；Vt為液壓缸兩腔總?cè)莘e；βe為油液的等效體積彈性模量；α為非對(duì)稱(chēng)缸比例系數(shù)。

忽略庫(kù)倫摩擦力等非線性負(fù)載，假設(shè)負(fù)載包括慣性和彈性負(fù)載，不考慮活塞黏性摩擦力和外加負(fù)載變化，液壓缸驅(qū)動(dòng)力F與負(fù)載的力平衡方程為

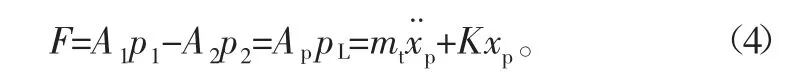
式中：p1為無(wú)桿腔壓力；p2為有桿腔壓力；Ap為液壓缸等效活塞面積，可近似取Ap=(A1+A2）/2；mt為折算到活塞軸上的活塞與負(fù)載的等效總質(zhì)量；K為負(fù)載的彈性系數(shù)。

由式（2）～式（4）可得伺服閥空載流量輸入、液壓缸驅(qū)動(dòng)力輸出的傳遞函數(shù)：

式（5）可表示為：

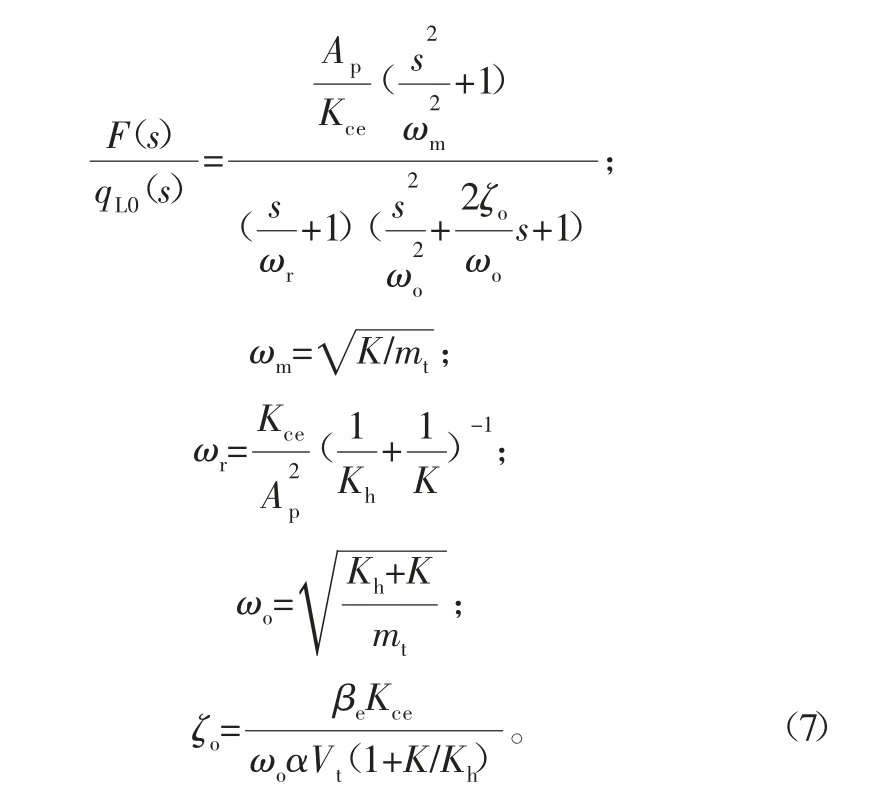
式中：ωm為負(fù)載的固有頻率；ωr為慣性環(huán)節(jié)轉(zhuǎn)折頻率；ωo為振蕩環(huán)節(jié)固有頻率，由液壓彈簧與負(fù)載彈簧并聯(lián)耦合與負(fù)載質(zhì)量形成；ζo為振蕩環(huán)節(jié)的阻尼比。

圖2為系統(tǒng)傳遞函數(shù)框圖，其中C(s）為控制器傳遞函數(shù)。

圖2 系統(tǒng)傳遞函數(shù)框圖

2 遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)系統(tǒng)辨識(shí)

2.1 BP神經(jīng)網(wǎng)絡(luò)辨識(shí)原理

BP神經(jīng)網(wǎng)絡(luò)一般為多層感知器模型，由輸入層、隱含層和輸出層組成，通過(guò)信號(hào)前向傳播和誤差反向傳播周而復(fù)始對(duì)網(wǎng)絡(luò)權(quán)值進(jìn)行動(dòng)態(tài)調(diào)整，使基于網(wǎng)絡(luò)輸出誤差的性能指標(biāo)函數(shù)達(dá)到最小，從而逼近系統(tǒng)輸入/輸出數(shù)據(jù)中的非線性映射，實(shí)現(xiàn)系統(tǒng)辨識(shí)建模[8]。圖3為BP神經(jīng)網(wǎng)絡(luò)辨識(shí)建模結(jié)構(gòu)，設(shè)電液力伺服系統(tǒng)為NARMAX（非線性擴(kuò)展自回歸滑動(dòng)平均模型），有

式中，P為樣本總量數(shù)。

2.2 BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

為了反映系統(tǒng)的動(dòng)態(tài)特性，并考慮系統(tǒng)的辨識(shí)精度，BP神經(jīng)網(wǎng)絡(luò)輸入層設(shè)4個(gè)神經(jīng)元，輸入值為d（k-1），d（k-2），u（k-1），u（k-2），輸出層為1個(gè)神經(jīng)元，為y（k）。選擇隱含層層數(shù)為1，隱含層節(jié)點(diǎn)選取要適中，節(jié)點(diǎn)過(guò)少，可能造成學(xué)習(xí)過(guò)程不收斂，系統(tǒng)辨識(shí)精度低；節(jié)點(diǎn)過(guò)多，則會(huì)影響學(xué)習(xí)速度，還會(huì)由于過(guò)擬合，造成網(wǎng)絡(luò)的容錯(cuò)能力及泛化能力的下降，因此確定神經(jīng)元個(gè)數(shù)為10。隱含層激勵(lì)函數(shù)為雙曲正切函數(shù)Tan-Sigmoid，輸出層激勵(lì)函數(shù)為線性函數(shù)Purelin。采用LM（Levenberg-Marquardt）算法進(jìn)行網(wǎng)絡(luò)參數(shù)學(xué)習(xí)，LM算法的初始自適應(yīng)學(xué)習(xí)率μ為0.001，最大訓(xùn)練次數(shù)為100，性能指標(biāo)函數(shù)選擇均方誤差mse。

圖3 神經(jīng)網(wǎng)絡(luò)辨識(shí)建模結(jié)構(gòu)

2.3 初始權(quán)值和閾值的遺傳優(yōu)化

遺傳算法從包含問(wèn)題的解集中隨機(jī)挑選一個(gè)群體作為初始群體，通過(guò)編碼將問(wèn)題的解轉(zhuǎn)換為染色體或個(gè)體，根據(jù)自然選擇和遺傳進(jìn)化機(jī)制從初始種群出發(fā)對(duì)個(gè)體進(jìn)行隨機(jī)選擇、交叉、變異操作，按照適應(yīng)度函數(shù)評(píng)估個(gè)體性能，對(duì)個(gè)體進(jìn)行篩選，使群體進(jìn)化到搜索空間中更好的區(qū)域，經(jīng)過(guò)不斷迭代，得到群體中的最優(yōu)個(gè)體作為問(wèn)題的最佳解[10-11]。

本文基于MATLAB全局優(yōu)化工具箱，遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值和閾值的步驟如圖4所示。

1）初始種群。

根據(jù)神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，采用實(shí)數(shù)編碼，對(duì)網(wǎng)絡(luò)的初始權(quán)值和閾值進(jìn)行編碼，編碼長(zhǎng)度為4×10+10+10×1+1=61，初始種群取值范圍為[-1,1],隨機(jī)產(chǎn)生100組長(zhǎng)度為61的實(shí)數(shù)序列，作為初始種群。

2）適應(yīng)度函數(shù)。

適應(yīng)度函數(shù)val（x）采用BP神經(jīng)網(wǎng)絡(luò)的性能指標(biāo)函數(shù)E，val（x）=E。

3）遺傳操作。

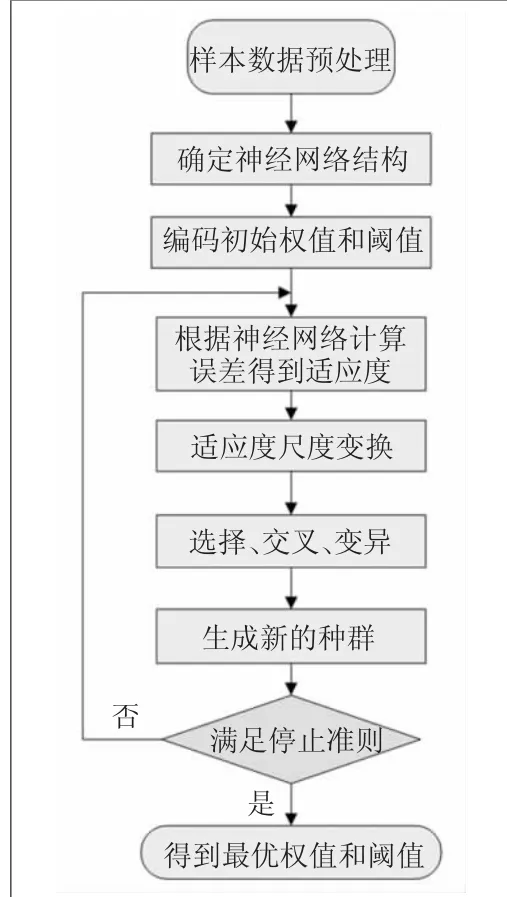
圖4 遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值和閾值

適應(yīng)度尺度變換函數(shù)把適應(yīng)度函數(shù)值轉(zhuǎn)換為適合于選擇函數(shù)使用范圍的值，包括排序、比率、最佳、線性變換等函數(shù)，選擇比率(Proportional）方式，返回值與個(gè)體的適應(yīng)度值大小成比例；選擇參數(shù)為遺傳算法挑選下一代的雙親，包括隨機(jī)均勻分布、剩余、輪盤(pán)賭、錦標(biāo)賽等函數(shù)，選擇隨機(jī)均勻分布(Stochastic uniform）方式，將每一個(gè)父輩根據(jù)適應(yīng)度值按比率布局在一條線上，算法以相同大小的步長(zhǎng)沿線移動(dòng)，根據(jù)降落的位置確定每一個(gè)父輩；優(yōu)良個(gè)體(EliteCount）確定將具有最佳適應(yīng)度值的個(gè)體遺傳到下一代的個(gè)體數(shù)，取5；交叉參數(shù)說(shuō)明父輩如何交叉基因產(chǎn)生子輩，包括分散、單點(diǎn)交叉、兩點(diǎn)交叉等，選擇分散(Scattered）函數(shù)，通過(guò)一個(gè)二進(jìn)制向量確定子輩基因來(lái)自于第一個(gè)父輩還是第二個(gè)父輩，交叉概率取0.8；變異參數(shù)指定算法如何通過(guò)小的隨機(jī)數(shù)創(chuàng)建變異子輩，包括高斯、均勻變異等，選擇高斯(Gaussian）函數(shù)，將一個(gè)高斯分布選擇的隨機(jī)數(shù)加到父輩的變異個(gè)體中，第一代方差尺度Scale取1，方差壓縮率Shrink取1。通過(guò)遺傳算法迭代，選取最后一代種群的最佳個(gè)體，解碼后將對(duì)應(yīng)的權(quán)值和閾值代入BP網(wǎng)絡(luò)進(jìn)行進(jìn)一步網(wǎng)絡(luò)訓(xùn)練。

2.4 系統(tǒng)辨識(shí)算法

在MATLAB中編寫(xiě)遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)系統(tǒng)辨識(shí)程序，代碼如下：

1)遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)主程序。

2)編碼函數(shù)程序。

將遺傳算法個(gè)體編碼為神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值。

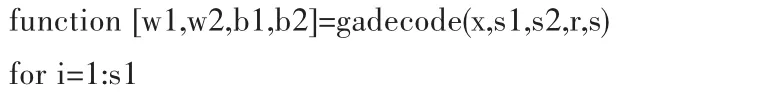
3)適應(yīng)度函數(shù)。

對(duì)每一代的種群進(jìn)行編碼，計(jì)算神經(jīng)網(wǎng)絡(luò)下的適應(yīng)度函數(shù)。

3 實(shí)驗(yàn)分析

搭建單通道電液力伺服系統(tǒng)實(shí)驗(yàn)臺(tái)架，加載形式選用液壓缸硬式連接自平衡框架，測(cè)力傳感器選用10 kN，液壓缸選用20 kN，油源壓力21 MPa，電液伺服閥為19 L/min；設(shè)置控制器為單位增益；對(duì)系統(tǒng)施加周期為3.33 s的方波信號(hào)，范圍為-5～+5 kN，信號(hào)采樣時(shí)間為0.01 s，獲取2664組實(shí)驗(yàn)數(shù)據(jù)。使用xlread函數(shù)將實(shí)驗(yàn)數(shù)據(jù)導(dǎo)入MATLAB工作空間，運(yùn)行系統(tǒng)辨識(shí)程序，圖5為神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，神經(jīng)網(wǎng)絡(luò)函數(shù)newff隨機(jī)將數(shù)據(jù)的70%用于訓(xùn)練，15%用于驗(yàn)證，15%用于測(cè)試，圖6為遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)訓(xùn)練的性能指標(biāo)函數(shù)曲線，網(wǎng)絡(luò)訓(xùn)練至第10代時(shí)網(wǎng)絡(luò)誤差已開(kāi)始收斂，驗(yàn)證數(shù)據(jù)的性能指標(biāo)函數(shù)最終為1.074×10-5。圖7為數(shù)據(jù)歸一化后系統(tǒng)實(shí)際輸出與網(wǎng)絡(luò)預(yù)測(cè)輸出的對(duì)比曲線，圖8為兩者的誤差曲線，系統(tǒng)誤差在0.06以?xún)?nèi)，均方誤差為1.497×10-5。

同時(shí)，借助MATLAB系統(tǒng)辨識(shí)工具箱[12]，選擇線性參數(shù)模型ARMAX（線性擴(kuò)展自回歸滑動(dòng)平均模型）對(duì)系統(tǒng)進(jìn)行辨識(shí)，模型階次［na nb nc nk］=［4 1 1 1］，采用預(yù)報(bào)誤差法，辨識(shí)結(jié)果為：

圖6 遺傳優(yōu)化神經(jīng)網(wǎng)絡(luò)訓(xùn)練的性能指標(biāo)函數(shù)曲線

圖7 實(shí)際輸出與網(wǎng)絡(luò)預(yù)測(cè)輸出對(duì)比曲線

圖8 誤差曲線

式中：y為系統(tǒng)實(shí)際輸出；y′為系統(tǒng)辨識(shí)輸出；mean表示求系統(tǒng)實(shí)際輸出的平均值；norm表示求向量的2-范數(shù)。

計(jì)算得到遺傳優(yōu)化神經(jīng)網(wǎng)絡(luò)模型擬合度值為99.5%，ARMAX模型擬合度值為86.04%。擬合度越高，系統(tǒng)辨識(shí)的結(jié)果越好，系統(tǒng)辨識(shí)輸出值越接近實(shí)際輸出值。

4 結(jié) 論

1）基于BP神經(jīng)網(wǎng)絡(luò)系統(tǒng)辨識(shí)建模方法不需了解系統(tǒng)內(nèi)部機(jī)理，較機(jī)理建模法效率更高。

2）遺傳算法的全局隨機(jī)搜索能力有效解決了單純BP神經(jīng)網(wǎng)絡(luò)收斂速度慢、易陷入局部極小的問(wèn)題，提高了算法的魯棒性、適用性。

3）遺傳優(yōu)化神經(jīng)網(wǎng)絡(luò)辨識(shí)模型較ARMAX模型辨識(shí)結(jié)果精度更高，適應(yīng)性更強(qiáng)，為系統(tǒng)控制策略的改進(jìn)和設(shè)計(jì)奠定了良好的基礎(chǔ)。