新時代數學教師學科素養之思考

鄢堅　林經武

【摘? 要】? 教育大計，質量為重;質量大計，教研為先。教研有為，教師專業素養為重。在技能大賽過程中呈現出教師對教材的個性化解讀，對課堂的駕馭與展開，對命題解題的專研，對教育教學理論的內化等都有一定的提升空間。新時代數學教師學科素養的養成需要與時代接軌，核心觀下的教師學科素養提升旨在促進教師在教學中開展深度思考，跳出事實性知識在數量上的累積，轉向對人的關鍵能力、思維品格、價值觀念的塑造。

【關鍵詞】? 數學教師;學科素養;專業技能

作為教研工作的引領者更要有教育人的責任與擔當。“培養什么人、怎樣培養人、為誰培養人”是新時代教育需要回答的根本問題，也是深化教育改革的初心所在。而這三個教育的基本問題需要通過教學來實現。“求木之長者，必固其根本;欲流之遠者，必浚其泉源。”。正所謂“坐而論道者需起而行之”。作為教育教學的實施者，如何承載國家的重任，人民群眾的希望成為我們不能回避的課題。教育大計，質量為重;質量大計，教研為先。教研有為，教師專業素養為重。

一、從福州市中小學教師教學技能大賽說起

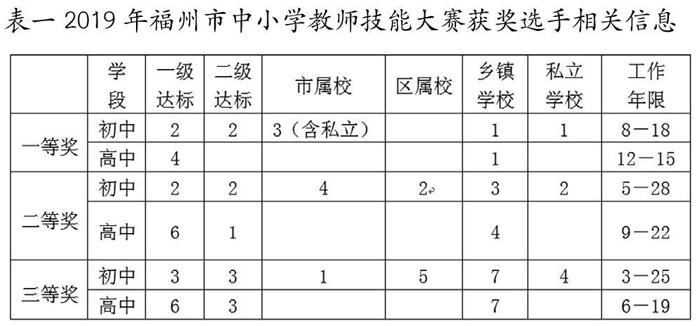
由福州市教育局、市工會、福州教育研究院聯合開展的2019年福州市中小學教師教學技能大賽落下帷幕，這次大賽折射出的變化，仍讓人感受到福州市中小學教師崗位大練兵的滾滾浪潮。我市數學科共有128人參賽，其中初中數學75人，高中數學53人。參賽學校涉及面廣，有省級校，市屬校，區屬校，鄉鎮學校及私立校等;年齡跨度大，最短3年，最長28年。在獲獎的學校中，市屬校與一級達標校獲獎名次與獎項均為主力軍，13個一等獎獲獎者工齡10年以上9人。一等獎者的教齡在8～18年限。我們也看到了一些鄉鎮學校與私立校中的苗子，而鄉鎮學校與私立校能獲獎的年限都比較長，如初中部私立校一等獎獲得者教齡18年，鄉鎮學校二等獎獲獎者教齡常達28年等，說明要成為教育的熟手還是要有一些經驗的積淀。除了經驗的積淀外，我們也看到了新時代數學教師的學科素養還有待提高。

比賽分成5個組，其中初中3個組，高中2個組。在人數多的情況下，初高中技能賽負責人多次研究比賽流程的公平性與隨機性，從評委與選手的輪換與抽簽，項目的評判標準與區間設置，到每個項目標桿的設置及選手抽簽的隨機性等都進行了詳細規劃。在片段教學與觀評課的標準設置中對沒有吃透數學課程標準、抓不住數學學科教學本質的選手得不到高分，引領教師關注課標，理解課程;學科技能操作項目，引領數學老師不僅會解題還會構題。三個比賽項目都直指教師的專業技能與學科素養考查。

二、數學教師應具備的學科素養

1.理解教材

考題1， 請根據以下內容，先設計片段教學內容，然后進行模擬教學（設計時間40分鐘，展示時間不超過10分鐘）。

課題：人教版九下第27章《相似三角形應用舉例》（P39～P40）內容中P40頁例5的教學部分進行面對評委的現場教學。

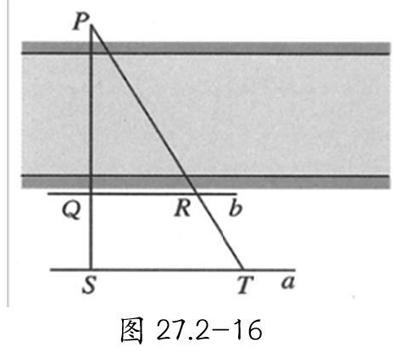
例5.如圖27.2-16，為了估算河的寬度，我們可以在河對岸選定一個目標點P，在近岸取點Q和S，使點P，Q，S共線且直線PS與河垂直，接著在過點S且與PS垂直的直線a上選擇適當的點T，確定PT與過點Q且垂直PS的直線b的交點R.已測得QS=45 m，ST=90 m，QR=60 m，請根據這些數據，計算河寬PQ.

命題意圖：考查教師如何創新使用教材，解讀教材的能力。

這是一道可以很好地區分答題者教材處理能力的題目，大部分老師只是根據自己的經驗講題，我們評委對片段教學評判編個順口溜：“本例題講好必須具備優秀生的思維，中等生的建模，潛力生的規范。”一般選手只能實現其中的一種或兩種。從比賽中可以看到不同生源層次的學校決定了老師在教學中采用的教學方法不同。教師能理解針對不同的生情選擇相應的教法，少見合理、有個性的創新的教學方法。

對本片段的處理：我們希望能看到以下的解讀：這是一個估算河的寬度的實際問題，教會學生將實際問題先抽象為數學問題。為了估算河的寬度，要關注三點：如何保證所求的長度是河寬？如何求河寬？所用的方法哪個是最優的？課本采用的方法是直接給予思路，為什么可以這么測量？教師要多做引導。本題采用的測量方法可以拓展到“全站儀”的原理（如圖1），因此對于本問題的數學理解還可以拓展為如何用全站儀來測量河寬。

中國高考評價體系中提道：在試題命制層面，需強調情境化設計，聯系學生日常生活實際、在現實的問題情境中考查學生核心素養的發展水平，從而推動關鍵能力和核心素養在教學和考試中的落實。如何落實，本案例就是很好的教學載體。

史寧中認為，“數學發展所依賴的思想在本質上有三個：抽象、推理、模型”。本道例題很好地解讀了史教授所說的數學三個基本思想。“用教材教”不等于“教教材”，教師應理解教材，通過對教材的個性化解讀，進一步領會到教材編寫者的意圖，理解教材設計的理念和背后蘊含的教育價值，拓展數學的理解，實現育人的價值。

2.掌握技能

考題2， 已知在⊙O中，弦AB⊥CD，垂足為E，連接BC，弦AM⊥BC，垂足為N，弦AM與CD相交于點H.

（1）如圖2，求證：DE=EH;

（2）如圖3，連接OC交AM于點K，當CD平分∠BCO時，

②如圖4，連接BH，CM，若tan∠HBE=S△BNH+S△CNM=求線段OK的長.

命題意圖：考查教師幾何性質研究的觀念——“對稱是一種觀念”;通過理解圓的對稱性（軸對稱性和中心對稱圖形性質），實際上把圓繞圓心旋轉任意角，所得的圖形都與原圖形重合，如何將圓的這種旋轉對稱性轉化為幾何元素的相等關系是本題考查的重點。因此解題的關鍵是理解弦圓共軸，以弧定角，能找到對稱軸，能通過圓上相等的弧找到相等的角。這種通過直線型的幾何元素將曲線的對稱性問題轉化為直線型的對稱問題的思維能力必須具備。考查教師研究幾何的脈絡;從定性到定量的研究過程。第一問與第二問的第一小題都是定性考查與圓相關的元素之間的關系，第二問的第二小題則定量考查與圓相關的角與線段的關系。考查幾何思維研究的同時還考查教師代數思維的理解——如何尋找同一量的不同表達等;考查邏輯思維、幾何直觀、運算求解等關鍵性能力。

考題的解決：對于（1）如圖5，連接AD.利用同角的余角相等，同弧所對的圓周角相等即可證得∠AHD=∠ADH，利用等腰三角形三線合一即可得到DE=EH.

對于（2）如圖6，連接DO并延長交AM于點T.先由已知的角平分線與圓中半徑所得的等腰三角形及外角的性質，結合直線型中平行線的判定與性質證得DT⊥AM，再利用圓中垂徑定理得到結論.

對于（3）如圖7，連接AD，OD，DB，DM，作OG⊥CD于G，記OD交AB于點S.由（1）（2）可知：∠BCD=∠DCO=∠MAB=∠BAD=∠ODC，設∠ODC=α，則∠AMD=∠MAD=∠OCB=2α，以弧導角可以得到∠AMD=∠ABD=2α，故∠BDE=90°-2α，∠ESD=90°-α，∠BDS=90°-α=∠BSD，∠HBE=∠DBE=2α.利用銳角三角函數求得邊角關系：tan∠BHE==tan∠BDE.

作答分析：本題參賽教師75人，只有1人做對。大部分的老師只解答到第（2）問。對于第三問看不出它是一個對稱的圖。無論是直線型中的線段DE=EH=HC還是弧線型的之間的關系發現不了，這是參賽老師的數感、直觀感及合情推理的素養欠缺。一個老師具不具備解題素養，主要看能否組合運用自己的本體性知識去解決復雜的問題。看起來是數學技巧的問題，但還是有問題的普適性問題，只要老師具有“對稱的眼觀”看待問題的數感、直觀感，再把問題分解到一個個節點上就不難解決。從答卷可以看到目前老師對題的認識只是在于解題，對題的價值及命題的意圖缺乏研究。教師對幾何教材的體系，發展的脈絡缺乏建構。

3.發展素養

考題3，觀評課（觀課與撰寫評課文稿總時長60分鐘）。

請觀看華東師大2011課標版《22.2.2用配方法解一元二次方程》教學實錄，從教學理念、教學實施、教學基本功等方面對該教學進行評價，撰寫不少于500字的評課文稿。

在短短的一個小時內選手們要完成相應內容實屬不易。從選手們的評課稿可以看出，絕大多數在賽前是有做過精心準備的，但也因此讓評委們見到了許多新八股，不少選手的評課稿可以用于任意一堂課，教育教學理論的支撐不足。當然也有一些選手在評課稿中說出自己的見解，談出建議，就像是一篇論文，既有標題、觀點，又用聽課過程中得到的信息來指證自己的教學觀，體現出選手扎實的教學基本功。但學科的素養、教育教學的理念缺乏，或是教學理念與思考淺表化，缺乏深度。缺少能觸及自身所持有的教與學的觀念層面的內容。

用配方法解一元二次方程教學中我們希望教師具備“生本”理念;一是以學生為本，關注學生對配方法探究過程能形成用已用知識與經驗探索解決問題的一般性方法，建立探索一般規律和數學建模的意識。二是教師的主導作用，教師引導學生如何從具體的數字系數到一般化完全平方式結構特征的發現。

三、新時代數學教師學科素養養成的建議

有追求：心中有大目標，不是為比賽而比賽，而是做到我盡力我無悔，以比賽為契機，以提高自己的專業技能與學科素養為目標，把每一次的培訓與學習轉化為提升自己學科素養的自覺行為。

多閱讀：多讀書。林語堂曾經說過：“讀書，開茅塞，除鄙見，得新知，增學問，廣識見，養性靈。”北宋著名詩人黃庭堅也說：“士大夫三日不讀書，則義理不交于胸中，對鏡覺面目可憎，向人亦言語無味。”因此即使是數學老師，不閱讀數學報刊，不學習教育教學理論，在教師的路上也難以走遠。

勇實踐：多聽課，每周下校聽各種類型的課或在國家教育資源公共服務平臺翻看各級的一師一優課，觀摩優秀教師的教學內容和做法，做到“好課共賞析，疑義相與析”。再根據自己的特點與所學的內容結合，逐步內化為自己的教學風格。多上研究課，多聽取同行對自己的評價。多反思自己的成就與不足。想一想，你課堂的效率如何？給學生思考的空間夠不夠？課下作業量大不大？習題的選擇是否符合課標的要求？等等。

常解題，無論是中考題還是競賽題多做多練多析多想。常解題，歸納通性通法，多剖題嘗試變式，多進行考試的備考與解構;多參與學科的命題和解題比賽等。

有目標，才有提升自我的動力;多閱讀，才有內在升華的積淀;勇實踐，才有知行合一的提升;常解析，才有體系脈絡的加深。新時代數學教師學科素養的養成需要與時代接軌，核心觀下的教師學科素養提升，旨在促進教師在教學中開展深度思考，只有深度思考才能跳出事實性知識在數量上的累積，轉向對人的關鍵能力、思維品格、價值觀念的塑造。

我們知道單是修煉教學基本功，就必須經歷從幼稚生硬到成長熟練，再到爐火純青的漫長過程。新時代數學教師學科素養的養成更需要和時代接軌。基礎教育關聯到千家萬戶，如何實現“五育”并全的培育方式，教師的專業技能與學科素養尤其重要。雖道阻且長，但勝在謀劃，足下有力，定能實現！

【參考文獻】

[1]陳子季.教育的根本問題——培養什么樣的人、怎樣培養人、為誰培養人[C].大學素質教育學刊（2018年4月8日第一期 總第23期）.中國高等教育學會大學素質教育研究分會，2018：22-28.

[2]教育部.義務教育教科書（九年級下冊）[S].北京：人民教育出版社，2015（01）：40.

[3]王剛.全站儀結構原理與發展分析[J].新建設：現代物業上旬刊，2013（10）：34-36.

[4]教育部考試中心.中國高考評價體系說明[S].北京：人民教育出版社，2019（11）：30-40.

[5]史寧中.數學思想概論（第1輯）：數量與數量關系的抽象[M].長春：東北師范大學出版社，2008（01）.

[6]喻平.數學關鍵能力測驗試題編制：理論與方法[J].數學通報，2019（12）：1-7.