一元線性回歸參數的估計

李秀蘭

（山西大同大學數學與統計學院，山西大同 037009）

變量間常見的關系有兩類：一類是確定性關系，這些變量間的關系是確定的，給定x的值，y的值唯一確定，可以用函數y=f(x)表示；另一類是相關關系，變量間有關系，但是不能用函數表示，也就是說，給定x的值，y的值不唯一確定。回歸分析就是研究變量間的相關關系的一門學科，它通過對客觀事物中變量的大量的觀察或試驗獲得的數據，去尋找隱藏在數據后面的相關關系，給出表達形式——回歸方程的估計[1-2]。

一元線性回歸的模型為

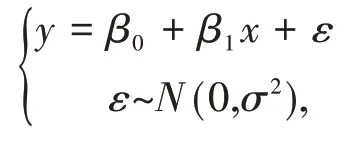
其中β0,β1,σ2未知參數,x是普通變量。

給定x的值xi,對y進行觀測,得y的值yi,i=1,…,n。

由數據對(xi,yi)估計出β0,β1,記為則可得y與x關系的一個估計

稱上式為回歸方程(經驗回歸函數),稱其圖像為回歸直線。

1 回歸系數的點估計

(1)最小二乘估計。

在x=xi處,y的實際值yi與回歸值的差異為=yi-β0-β1xi，令

Q(β0,β1)=應該滿足

引入記號

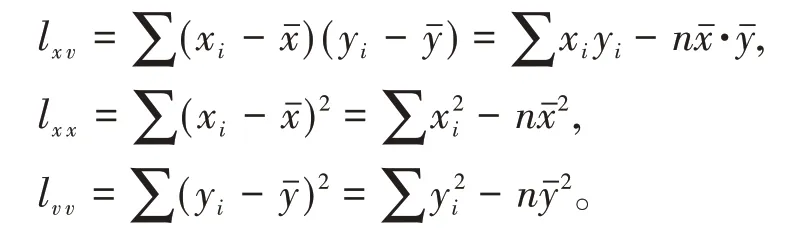
對β0,β1求偏導并令其為0，得正規方程組

整理得

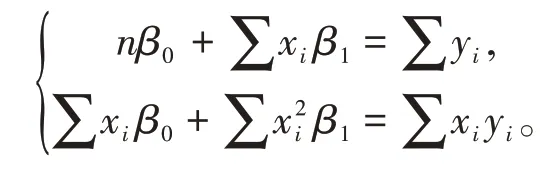
解方程組得

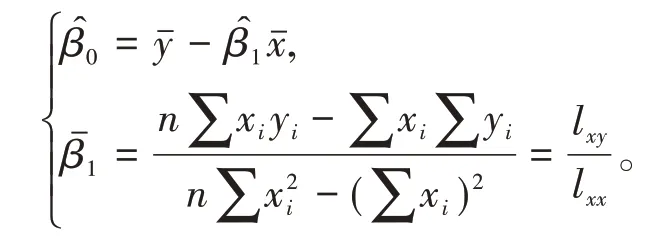
(2)回歸系數的最大似然估計。

似然函數為

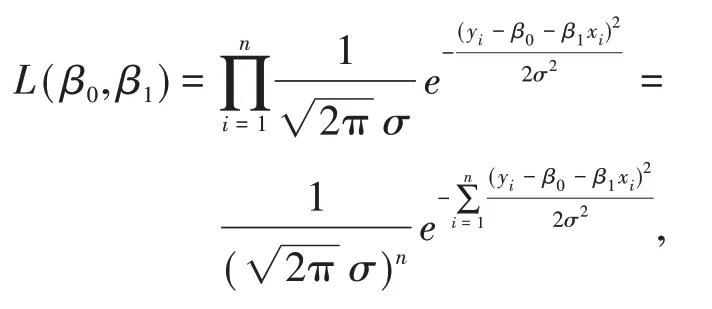
兩邊取對數得

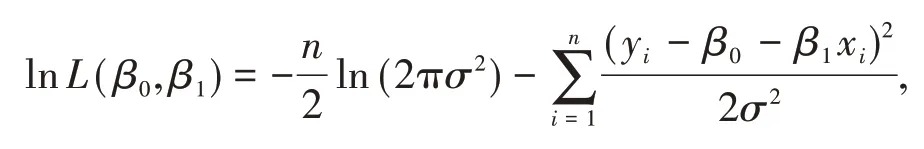
對β0,β1,σ2求偏導并令其為0，得

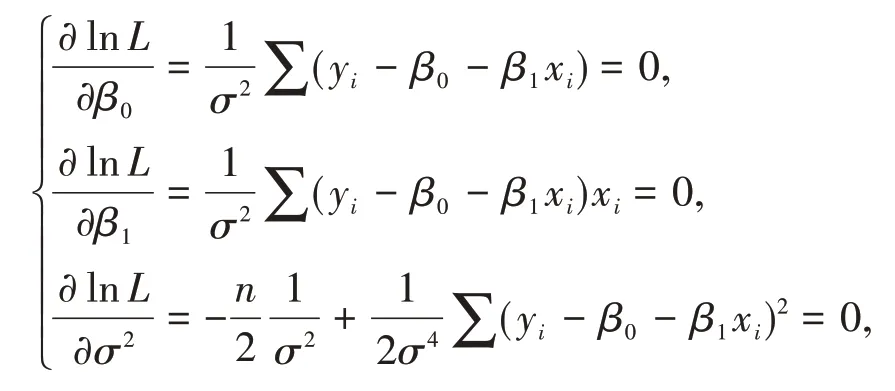
解方程組得

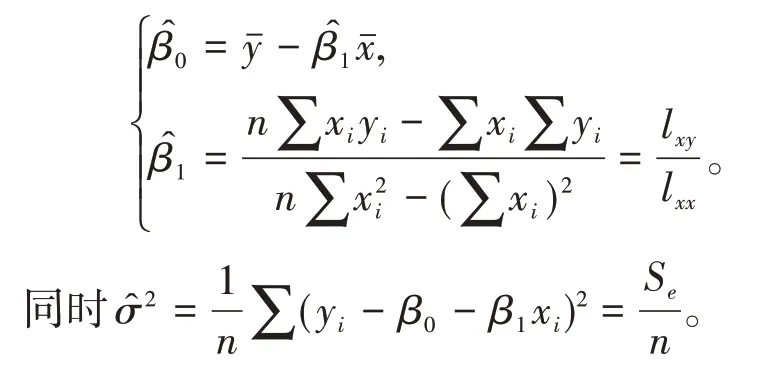
可以看到在隨機誤差服從正態分布時，參數的最小二乘估計與最大似然估計一致的，但是如果不知道隨機誤差的分布時，最小二乘估計還與上面的結果相同，但此時不能求最大似然估計。

2 回歸系數的區間估計

引理1設yi=β0+β1xi+εi,i=1,2,…,n,εi～N(0,σ2),各εi間獨立，則

顯然Se/(n-2)是σ2的無偏估計;

為了得到β0,β1的區間估計，可以考慮t分布樞軸量

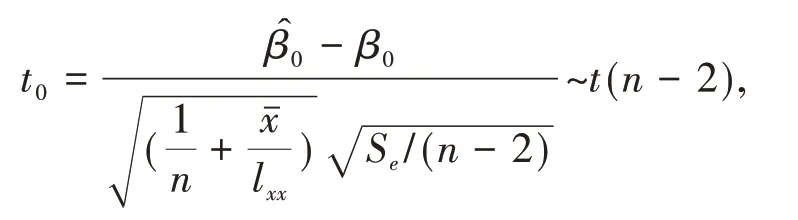
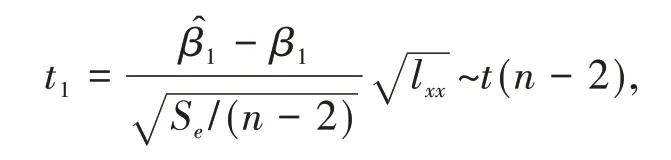
對于給定的置信水平1-α，查表得t1-α/2(n-2)，從而可以得到β0的置信區間是

對于給定的置信水平1-α，查表得F1-α(1,n-2)，從而可以得到β0的置信區間是