偶極子聲波測井在套管井中的聲場特征?

陳雪蓮 邵歡歡 張聰慧 祁 曉 李盛清 張淼鶴

(1 中國石油大學(華東)地球科學與技術學院 青島 266580)

(2 中國石油大學(華東)深層油氣重點實驗室 青島 266580)

(3 中海油田服務股份有限公司 廊坊 065201)

0 引言

近年來，偶極子聲波測井已廣泛應用于裸眼井和套管井中，其在地層橫波時差提取、各向異性反演以及儲層壓裂評價等方面取得了較好的應用效果[1?9]。Chen等[10]最早通過現場測量的偶極陣列波形，分析了套管井中的偶極子聲場特征，并將裸眼井和下套管后測量的波形數據進行了對比，驗證了在套管井中測量地層彎曲波的可行性。Schmitt[11]考察了偶極子聲源在不同膠結狀況套管井中激發的模式波，并將水泥膠結差時出現的套管一階彎曲波稱作流體環彎曲模式。李剛等[12]和吳洋等[13]對套管井中地層彎曲波的頻散進行了詳細的研究，指出下套管后地層彎曲波的頻散曲線向高頻偏移，并研究了膠結水泥密度對地層彎曲波頻散特征的影響。目前，人們在套管井中進行偶極子聲波測井主要用于套后地層評價，沒有關注如何利用偶極子陣列波形進行水泥的膠結質量評價。由于全球各地油田存在大量套管井，研究套管井中的水泥膠結情況對于已有油田的挖潛和改造工作具有重要的指導和實用意義。

針對目前套管井中越來越多的偶極測井數據，研究利用偶極數據做固井質量評價也越來越得到重視。水泥膠結/聲波變密度測井(Cement bonding logging/variable density logging,CBL/VDL)技術采用單極子聲源作發射器，單極子聲源是一種軸對稱聲源，激發縱向模態的套管波[14]，主要利用套管波的幅度或衰減評價與套管直接接觸的水泥第一界面的膠結質量的好壞。偶極子聲源是一種指向性聲源，其在套管井中激發的模式波衰減比較小，尤其是低階套管彎曲波，其傳播速度低且幾乎不泄漏能量，其相速度或頻散特征對膠結狀況敏感。Wang等[15]模擬了不同流體環厚度對套管彎曲波頻散的影響，觀測到隨著水泥膠結越差，套管彎曲波的相速度越高；Doug等[16]從實際數據中提取到了套管彎曲波的頻散曲線；Naoki等[17]通過實際數據分析了流體環厚度對套管彎曲波以及地層彎曲波頻散曲線的影響。本文將理論計算和現場測量數據相結合，模擬了偶極子聲源在套管井中不同膠結情況下的地層彎曲波和套管彎曲波的傳播特征；分析了水泥環第一界面和第二界面分別膠結差時兩種模式波的頻散、衰減以及激發強度的變化規律；以及在水泥環第一界面膠結差的情況下，第二界面流體環厚度變化時兩種模式波的變化趨勢，并進一步探討了在套管井中利用偶極子聲波測井數據同時評價水泥環兩個界面的膠結狀況的可行性。

1 套管井中偶極子聲波測井的基本理論

圖1給出了套管井充液井孔的模型示意圖(以I界面膠結差、II界面膠結好為例)。采用柱狀徑向分層聲學模型，模型由內向外介質依次為井內流體、套管、流體環、水泥環和地層，各介質的外徑分別為r1、r2、r3、r4和無窮大，模擬所用的井孔和地層相關參數見表1。對于同心層狀的軸對稱套管井模型，利用實軸積分法可以模擬井內偶極子聲源激發的聲場。在柱坐標系下模型內固體層的位移和應力分量定義為

表1 模型參數(I界面差、II界面好情況)Table 1 Model parameters for poor bonding at the first interface and good bonding at the second interface

圖1 I界面膠結差套管井模型示意圖及井孔截面示意圖Fig.1 Model of the cased borehole with poor bonding at the first interface and good bonding at the second interface,and cross section of the model

其中，T表示位移和應力組成的矢量/矩陣的轉置。對于模型中的每一層固體，位移和應力可以表示為

式(2)中，M是6×6的系數矩陣，X=(An,Bn,Cn,Dn,En,Fn)T，分別代表層內反射和入射的縱波、SH橫波以及SV橫波的振幅系數，流體層中只有縱波(An和Bn)、最外層的地層只有向外擴散的輻射波(Bn、Dn和Fn)。在膠結良好的固固界面，位移和應力分量均連續，即

其中，j表示第j層，r是界面的徑向位置。根據Thomson-Hanskell傳遞矩陣[18]，多層固體耦合時可將內層固體聲學影響傳遞到外層固體，減少求解方程的矩陣維數。由于液體中不傳播橫波，液體與固體界面的邊界條件中只有徑向位移u及徑向應力σrr連續，剪切應力σrθ和σrz均為零。例如，L層液體層兩側的固液和液固界面的連接方程可表示為

以套管與水泥之間充填流體為例，給出套管井井孔聲場的計算方法，井內泥漿、套管、流體環、水泥以及地層分別設為第1、第2、第3、第4和第5層。水泥內的矢量S可以傳遞到井外地層中，用地層中的振幅系數(Bn、Dn和Fn)表示，如式(5)所示：

其中，M矩陣表達式可參見文獻[19]。iL或iR(i=3,4,5)表示第i層的左邊界或右邊界的徑向位置，3個矩陣M相乘得到一個4×3矩陣，其表示了式(6)的系數矩陣N(9)(10)～N(12)(10)、N(9)(11)～N(12)(11)和N(9)(12)～N(12)(12)。

井內泥漿與套管、套管與流體環以及流體環與地層之間的3個液固界面，可直接建立如式(6)所示的12×12矩陣方程，等號的右端表示井內聲源產生的直達波場。

求解式(6)可得到套管內的反射系數用于計算套管內的聲場，在柱坐標(r,θ,z)中，套管內聲場勢函數?n在頻率域中的表達式如下：

其中，n=1代表偶極源，εn=2；f為井孔內流體的徑向波數，r0為偶極距，kz為軸向波數；第一類n階貝塞爾函數In代表由井壁向井軸會聚的波，第二類n階變型貝塞爾函數Kn代表向井外傳播的波或發散波，SR(ω)為聲源函數，在全波波形計算時選擇高斯源的譜函數。

式(6)中的系數矩陣N是頻率和波數的函數，其行列式等于零時的方程det(N(ω,kz))，即為圖1模型中模式波的頻散方程，求解此方程可得到套管和地層彎曲模式波的頻散曲線。模式波的相速度、衰減可由模式波極點所對應的波數kz得到，見式(8)所示，激發強度見式(9)：

2 偶極子聲源在套管井中激發的模式波分析

2.1 自由套管模型下井孔模式波的頻散特征

與裸眼井情況相比，偶極子聲源在套管井中激發的聲場更加復雜，在膠結不好的井段除了地層彎曲波還可記錄到套管彎曲波，Schmitt[20]也將其稱為流體環彎曲模式。圖2(a)顯示了自由套管井(套管與地層之間完全充填泥漿)中套管彎曲波的頻散曲線(實線是相速度，虛線是群速度，同一種顏色的曲線代表同一個模式)。在頻段0～20 kHz范圍內套管彎曲波可存在3階模態，現在的偶極子陣列聲波中偶極子源的中心頻率在3 kHz左右，一般可記錄到最低階套管彎曲模式，二階和三階套管彎曲波存在截止頻率，截止頻率與井眼直徑和套管的橫波速度有關。圖2(b)給出了套管外為自由邊界時套管一階彎曲模式與套管外耦合泥漿時頻散曲線的對比，可見套管外耦合泥漿與空氣相比套管彎曲波的相速度明顯降低。圖3是地層彎曲波的頻散曲線，與裸眼井地層彎曲波的頻散曲線相比，套管的存在使得頻散曲線向高頻移動，膠結良好與自由套管相比頻散曲線向高頻偏移得更多，類似井眼半徑縮小后的頻散曲線。

圖2 自由套管井中套管彎曲波的頻散曲線Fig.2 Dispersion curves of casing flexural waves in free pipe

圖3 自由套管井中地層彎曲波的頻散曲線Fig.3 Dispersion curves of formation flexural waves in free pipe

2.2 套管與水泥環(第I界面)膠結差時井孔模式波的傳播特征

在套管與水泥環之間加入一層流體環(泥漿)模擬第一界面膠結差的狀況。圖4為I界面膠結差、II界面(水泥環與地層)膠結好時地層彎曲波的頻散曲線和衰減曲線。結果顯示，隨著流體環厚度的增加，頻散曲線向低頻偏移，且流體環的存在使得截止頻率附近地層彎曲波的衰減(1/Q)增加，艾里相附近的衰減降低。

圖4 I界面膠結差、II界面膠結好時地層彎曲波頻散曲線和衰減曲線Fig.4 Formation flexural wave in cased borehole with poor bonding at the first interface and good bonding at the second interface

當I界面存在流體環時便可以激發出套管彎曲波，圖5是I界面膠結差、II界面膠結好時套管彎曲波(最低階)的頻散曲線和衰減(1/Q)曲線。圖5(a)顯示，隨著流體環厚度的增加，最低階套管彎曲波的相速度和群速度均逐漸增大，并且其對流體環厚度變化非常敏感，這一特征為利用套管彎曲波的相速度反演流體環厚度提供了可能。與圖4(b)相比，套管彎曲波的衰減值明顯低于地層彎曲波的衰減值，這與套管彎曲波的相速度較低且幾乎不泄漏能量有關。為了進一步分析偶極子聲源在套管井中激發的全波波形特征，圖5(c)還顯示了套管彎曲波的激發強度。隨著流體環厚度的增加，套管彎曲波的激發強度逐漸增大，同一流體環下其隨著頻率的增加逐漸降低，流體環厚度越薄幅度下降得越快。

圖5 I界面膠結差、II界面膠結好時套管彎曲波頻散、衰減和激發強度曲線Fig.5 Casing flexural wave in cased borehole with poor bonding at the first interface and good bonding at the second interface

為了進一步考察流體環厚度對激發波場的影響，對第I界面流體環厚度變化時偶極子聲源激發的全波波形進行模擬，結果如圖6所示。源距為3 m、源函數為中心頻率為3 kHz的高斯源，頻帶寬度是中心頻率的0.3倍。從圖6中可清晰地觀測到地層彎曲波波包和套管彎曲波波包，并且隨著流體環厚度的增加，地層彎曲波相速度稍有降低，到時滯后，但套管彎曲波的相速度明顯增加；在自由套管狀況下，地層彎曲波和套管彎曲波疊加。此外，隨著流體環厚度的增加，套管彎曲波幅度逐漸增強，這一特征與圖5(c)所示的激發強度特征相吻合。圖7為將流體環厚度為1 mm時的全波放大顯示，從圖7中可看出套管外存在1 mm流體環條件下套管彎曲波仍清晰可見。地層彎曲波的頻散特征是低頻成分傳播快，而套管彎曲波是高頻成分傳播快，這一傳播特征在全波波形中體現得特別明顯。隨著頻率的降低套管彎曲波的幅度也逐漸增加，這也與圖5(c)顯示的激發強度隨著頻率降低而逐漸增大的現象一致。

圖6 I界面膠結差、II界面膠結好時與自由套管和膠結良好情況下的全波列波形Fig.6 Waveforms simulated for cased borehole with different cement-bond conditions:the first interface is in poor cement and the second interface is in good cement,free pipe,and good bonding,respectively

圖7 I界面外流體環厚度為1 mm時的全波列波形Fig.7 Waveforms simulated for cased borehole with the fluid ring thickness of 1 mm at the first interface

2.3 水泥環與地層(第II界面)膠結差時井孔模式波的傳播特征

在水泥環第I界面膠結良好、第II界面膠結差時，仍可激發出套管彎曲模式波，圖8是套管彎曲波的頻散、衰減和激發強度曲線。隨著水泥環第II界面流體環厚度的增加，套管彎曲波的相速度和群速度均逐漸增大，這一規律與水泥環第I界面膠結差時相似。但同一流體環厚度下水泥環第II界面膠結差時的激發強度略低于第I界面膠結差的激發強度，這是由于水泥環第II界面膠結差時套管的彎曲振動勢必攜帶水泥環一起振動，其附重增大造成套管彎曲波的振動幅度降低。

圖8 水泥環第II界面膠結差時套管彎曲波的頻散、衰減和激發強度曲線Fig.8 Casing flexural wave in cased borehole with good bonding at the first interface and poor bonding at the second interface

水泥環第II界面膠結差時，與膠結良好時相比，地層彎曲波的頻散曲線也明顯地向低頻方向偏移，如圖9所示。在低頻段隨著第II界面流體環厚度的增加相速度稍有降低，高頻段相速度稍有增大；其衰減隨著流體環厚度的增加逐漸增大。與水泥環第I界面膠結差時相比，地層彎曲波相速度對水泥環第II界面流體環厚度的變化不敏感，這從圖10所示的全波波形中也可觀測到，流體環厚度變化時地層彎曲波的變化很小，套管彎曲波隨著流體環厚度的變化趨勢與第一界面膠結差時類似，但波形幅度明顯降低。

圖9 水泥環第II界面膠結差時地層彎曲波的頻散曲線和衰減曲線Fig.9 Formation flexural wave in cased borehole with good bonding at the first interface and poor bonding at the second interface

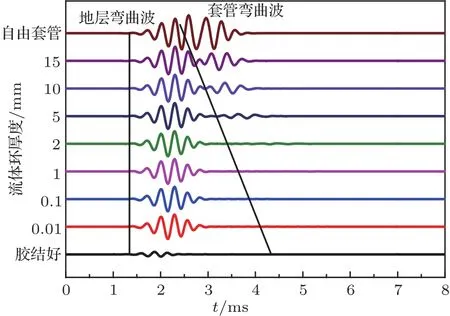
圖10 I界面膠結好、II界面膠結差時與自由套管和膠結良好情況下的全波列波形Fig.10 Waveforms simulated for cased borehole with different cement-bond conditions:the first interface is in good cement and the second interface is in poor cement,free pipe,and good bonding,respectively

2.4 探討水泥環第I界面膠結差時井孔模式波對第II界面膠結狀況的敏感性

為了進一步分析在水泥環第I界面膠結差時利用偶極子聲波測井評價水泥環第II界面膠結質量的可行性，圖11對比了水泥環第I界面膠結良好和存在1 mm流體環時，地層彎曲波和套管彎曲波的頻散曲線隨水泥環第II界面流體環厚度增加時的變化趨勢。當水泥環第I界面存在1 mm的流體環時(圖11中標注的I界面膠結差)，低頻下地層彎曲波的相速度與膠結良好時相比降低，這與圖11(c)顯示的全波波形中地層彎曲波的相速度明顯滯后相吻合；在8～20 kHz頻段隨著第II界面流體環厚度的增加，地層彎曲波的相速度逐漸增大；與水泥環第I界面膠結好時相比，第I界面膠結差時對于相同的流體環厚度變化范圍，相速度的動態變化范圍增加，即第I界面流體環的存在，提高了高頻地層彎曲波對第II界面流體環厚度變化的敏感性。但在較高的工作頻率下套管彎曲波的高階模態會被激發，使得波形成分復雜。套管彎曲波的相速度隨著水泥環第II界面流體環厚度的增加逐漸增大，但其受到第I界面膠結差的影響，其相速度從第I界面存在1 mm流體環時套管彎曲波的相速度開始逐漸增加；與水泥環第I界面膠結良好時相比，第I界面膠結差時低頻下套管彎曲波的相速度稍有增大，但當第II界面流體環厚度較大時(如圖11(b)中流體環厚度為5 mm、10 mm和15 mm)，高于4 kHz后套管彎曲波的相速度與第I界面膠結良好時相比降低。圖11(d)是套管彎曲波的激發強度，可見水泥環第I界面流體環的存在提高了套管彎曲波的激發強度，這與圖11(c)中紅色波列顯示的套管彎曲波幅度稍高的響應特征一致。

傳統的VDL或多極子陣列聲波測井中，根據其單極模式下測量的套管波速度可較好地判別水泥環第I界面是否膠結良好。當水泥環第I界面膠結差時套管波速度接近57μs/ft，第I界面膠結良好第II界面膠結差時套管波速度明顯降低，但單極子聲波測井測量的全波波形在水泥環第I界面膠結差時很難判斷水泥環第II界面的膠結狀況。對比圖11(a)和圖11(b)可見，在確認水泥環第I界面膠結差時若水泥環第II界面也膠結差，則地層彎曲波的相速度會比第II界面膠結良好時低，且在水泥環第I界面膠結差時，套管彎曲波的相速度仍對第II界面流體環厚度的變化敏感，這為在水泥環第一界面膠結差時評價水泥環第二界面的膠結質量提供了可能。

圖11 水泥環第I界面膠結好和差時水泥環第II界面流體環厚度變化對井孔模式波的影響Fig.11 In fluence of thickness variation of the second-interface fluid ring on borehole mode waves for the good and poor bonding at the first interface,respectively

3 實例分析

圖12(a)是某井測量的偶極波列圖，接收的陣列波形中最近的源距是3.625 m，間距是0.1524 m，套管外徑和厚度分別為19.3675 cm和1.016 cm，井眼直徑是24.13 cm，通過CBL/VDL可知套管波相對幅度約40%，所研究井段的水泥環第I界面膠結差。在圖12(a)顯示的全波列波形中可較清晰觀測到泄漏縱波、地層彎曲波以及套管彎曲波，對此波形做時間-慢度(圖12(b))以及頻率-慢度(圖12(c))相關分析，觀測到了地層彎曲波以及套管彎曲波。在已知套管井各層介質的參數下，給定水泥環第一界面5 mm流體環厚度時理論計算的套管彎曲波的頻散曲線(圖12(c)中的實線)與實際波形提取的頻散曲線(圖12(c)中的離散點)吻合度較高，可推斷此深度點水泥缺失的等效厚度接近5 mm(實際井中流體環厚度可能不規則)。

圖12 現場實例分析Fig.12 Analysis of the field data

4 結論

本文利用實軸積分法計算得到了套管井中偶極聲源激發的全波波形，模擬了偶極子源在套管井不同膠結條件下的模式波傳播特征，分析了地層彎曲波和套管彎曲波的頻散、衰減和激發強度等響應特性，得到以下認識和結論：

(1)與裸眼井相比，下套管后地層彎曲波的頻散曲線向高頻偏移，膠結良好時的頻移量最大。

(2)在水泥環第I界面或第II界面膠結差時，接收的波列中會觀測到套管彎曲波，其頻散特征是低頻成分波的傳播速度低于高頻波，激發強度隨著頻率的增加快速降低，頻散趨勢類似于單極斯通利波；當套管與水泥環或水泥環與地層之間的流體環厚度增加時相速度逐漸增大，套管彎曲波的相速度對流體環厚度的強敏感性為利用套管彎曲波的相速度反演流體環厚度提供了可能。

(3)在已知地層聲學性質、井眼和套管參數后，可嘗試通過將現場測量偶極波形數據提取的彎曲波頻散曲線與理論模型計算的頻散曲線相擬合估算水泥環界面的流體環等效厚度，反演結果也將反映水泥缺失的程度。