基于自適應動態規劃的反高超武器微分對策制導律

孫磊，付斌，萬士正，常曉飛，閆杰

(西北工業大學 航天學院， 西安 710072)

0 引 言

隨著各國高超聲速飛行器技術的發展，各型演示驗證項目的武器化進程不斷加快，以我國的“DF-17”、俄羅斯的“先鋒”為代表的高超聲速武器已經陸續進入到現役武器裝備行列。相比于傳統武器，高超聲速武器具有飛行速度極快、自主博弈機動能力強、飛行彈道多變等突出特性，在對其進行攔截時，傳統攔截制導方法攔截能力弱，使得我軍在反高超聲速武器攔截作戰中，以“一對一”進行攔截時任務失敗風險較大，以“多對一”進行攔截時，綜合作戰效能較低。

為了解決高超聲速武器的攔截問題，研究人員提出了許多新型制導方法。李炯等[1-2]針對反高超聲速武器攔截制導問題設計了一種非奇異快速終端二階滑模制導律，并且針對側窗探測的動能攔截反高超聲速武器設計了一種制導律，其在對目標進行攔截時需要始終保證導引頭側窗對于目標的指向，從而實現對目標的探測；葉繼坤等[3]基于經典的微分幾何理論，對末制導中的彈目運動模型進行了空間幾何分析，并設計了二階滑模微分幾何制導律，克服了不確定性的影響，保證了系統的魯棒性和制導精度；雷虎民等[4]針對反高超聲速武器攔截問題，設計了一種基于零控脫靶量在有限時間收斂的制導方法，通過自適應滑模理論與有限時間穩定控制理論的結合，選擇解耦的縱向面與水平面上的零控脫靶量作為滑模面，給出了制導律形式，并且證明了制導律的有限時間收斂特性。

上述方法均將目標的突防策略考慮為一種固定的機動模式，當未來戰場中，目標的機動將會更加智能，可能會針對我方機動而選擇更加有針對性的突防策略。因此研究人員開始研究一種基于博弈微分對策的博弈制導方法。花文華等[5-6]基于變速導彈模型的非線性情況進行了制導律設計，并通過選取合適狀態量對模型進行了線性化，推導出了微分對策制導律形式，還針對帶有攻擊角約束的情形進行了微分對策問題的指標設計，并通過系統的降階，實現了解析形式的制導律求解；李遷運等[7]針對大氣層內直/氣復合飛行器進行了微分對策制導問題中，直/氣復合控制系統對策空間分布的研究，并對策略空間進行了優化；Y.Oshman等[8]基于微分對策理論設計了一種針對未來高機動無人作戰飛行器的制導方法，其主要創新點是采用了通過對目標姿態信息的解譯，實現了對目標飛行狀態的估計；A.Green等[9]在水平面內設計了一種追逃制導律，追逐方帶有末端速度要求，逃逸方速度恒定但是帶有機動能力，并根據追逃雙方的初末條件給出了最優制導策略；V.Turetsky等[10]針對未來可能出現的強機動能力彈道導彈攔截問題，分析了兩種基于追逃對策的制導律，對比結果顯示，在相同的初始條件與參數下，僅考慮零控脫靶量作為性能指標的制導律所形成的攻擊區較考慮能量最優的制導律有更大的攻擊區。另外還有許多研究者采用了微分對策問題的建模方法進行制導律設計，但是在求解過程中多數都是采用了簡化的非線性模型或者是近似模型，其求解精度在一定程度上會受到影響。

為了更好地求解微分對策條件下的納什均衡解，研究者引入自適應動態規劃(Adaptive Dynamic Programming,簡稱ADP)算法對這類最優化問題進行求解[11-17]，其中Sun J等[18-19]在攔截制導中采用自適應動態規劃算法，但是其所選用的回報目標是終端零控脫靶量最小，而本文所采用的方法是每一時刻的視線角速度最小，相較之制導過程更平穩。

ADP算法具有求解速度快、計算精度高等優點，能夠很好地應用于制導律設計過程。本文針對高超聲速目標機動打擊特點，采用自適應動態規劃的方法進行攔截彈制導律求解。首先，針對高超聲速目標攔截問題中的連續非線性問題進行微分對策問題建模；然后，利用近似動態規劃算法對連續非線性系統微分對策問題進行求解；最后，基于高超攻防對抗對所給出的方法進行仿真驗證。

1 微分對策制導問題建模

為了準確地描述微分對策問題，從而進行解的求取，需要對攔截彈與目標進行攔截相對運動的微分對策問題建模。

1.1 彈目相對運動關系建模

為了方便地描述末制導階段的彈目相對運動，從而給出制導律推導時所需要的部分運動方程，本節對彈目相對運動關系進行簡單的描述和定義。為了簡化推導，一般可以將縱向與橫側向平面直接解耦后分開考慮。在縱向平面內，末制導階段縱向平面內彈目運動關系如圖1所示。

圖1 末制導階段縱向平面內彈目運動關系

圖1中，Ox軸與Oy軸構成了彈目遭遇平面，攔截彈以質點M表示，其速度為VM，速度傾角為θM；在垂直于速度的方向上，攔截彈具有加速度aM；高超聲速飛行器目標以質點T為表示，其速度為VT，速度傾角為θT；在垂直于速度的方向上，高超聲速飛行器具有加速度aT；彈目相對距離為R，彈目視線角為q。

彈目間相對位置按照極坐標表達形式(R,q)的數學表達式為

(1)

(2)

在推導過程中，攔截彈與目標的運動模型也可以簡化的表示為

(3)

攔截彈的速度VM與目標的速度VT在末制導階段也可以認為是不再變化的。

對式(2)求導，可得：

(4)

將式(3)代入式(4)可得：

(5)

整理后可得：

(6)

選取系統狀態為

(7)

系統狀態方程可以寫為

(8)

1.2 微分對策問題一般化描述

針對式(8)考慮連續非線性系統為

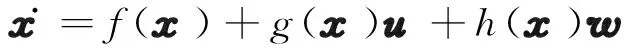
(9)

式中：x∈Rn為狀態向量；u∈Rm為控制向量；w∈Rp為擾動向量；f(x)∈Rn、g(x)∈Rn×m、h(x)∈Rn×p均為光滑可微函數，分別為系統內動態方程、控制方程與擾動方程。

定義指標函數為

(10)

當追逃雙方對于某一狀態x(t)，采用控制策略u(x)與擾動策略w(x)時，可以用狀態值函數(如式(11)所示)對追逃策略進行評價。

(11)

對式(11)求導后可得：

(12)

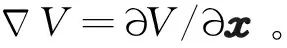
可以定義漢密爾頓函數為

H(x,u,w)=U(x,u,w)+

(13)

假設這個微分對策問題有唯一的鞍點解，且鞍點解滿足納什平衡條件，如式(14)所示。

(14)

則根據Bellman方程最優性原理，有如下關系：

(15)

對于u*與w*必須滿足最優性必要條件為

(16)

可以得到最優解形式如式(17)所示。

(17)

將式(16)、式(17)中的最優控制u*與w*代入漢密爾頓方程，得到：

xTQx+

(18)

2 連續非線性系統微分對策問題的近似動態規劃解法

2.1 自適應動態規劃算法流程

對值函數的表達式進行變形得到：

(19)

此時，納什平衡條件可以重新整理為

(20)

根據自適應動態規劃算法中常用的值迭代算法，有如下求解流程：

(1) 對于狀態S初始化值函數，并計算t+T時刻的值函數；

(2) 根據t+T時刻值函數，以及t時刻的獎勵函數U，計算當前時刻值函數的估計目標值；

(3) 根據目標值修正值函數的估計函數；

(4) 根據值函數修正值計算最優策略值。

值函數更新公式為

(21)

策略更新公式為

(22)

基于上述方法，設計一個Actor-Critic架構的算法框架，通過對基于神經網絡的評價函數進行值迭代，不斷地優化出一個最優的值函數，示意圖如圖2所示。

圖2 自適應動態規劃算法的Actor-Critic架構

2.2 自適應動態規劃算法實現

本文給出值函數的神經網絡近似形式的表達式為

(23)

式中：σ(x)為神經網絡擬合基函數，以狀態的4次項的齊次形式進行狀態組合，需要設置對應的權值WVi。

值函數關于狀態的偏導數則可表示為

(24)

按照值迭代公式，可以計算得到當前時刻的目標狀態值函數更新值應為

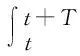
(25)

當前時刻的狀態值函數神經網絡近似值為

(26)

近似誤差為

(27)

為了采用誤差值對近似神經網絡進行修正，本文采用梯度下降法，建立誤差指標函數為

(28)

根據梯度下降法，給出值函數神經網絡的權值修正算法為

(29)

式中：αV為學習率，表示對于梯度下降的比率更新。

其中，

(30)

3 末制導仿真

3.1 仿真參數設置

為了驗證自適應動態規劃算法的有效性，進行基于數字仿真的實驗驗證。仿真初始條件如表1所示。

表1 仿真初始條件

3.2 對比制導律方法簡介

周狄[20]提出的基于滑模變結構方法的最優滑模制導律(Optimal Sliding Mode Guidance，簡稱OSMG)在制導攔截問題中表現出了優異的特性，相比于增廣比例導引算法，其不需要知道目標機動的具體大小，可根據當前狀態與滑模面的關系自適應給出相應的補償機動。OSMG制導下的攔截彈會按照給定的滑模面趨近于目標，OSMG算法具有較高的攔截精度，并且其需用過載相比于比例導引類算法而言會更小。其表達式為

(31)

3.3 仿真結果與分析

考慮目標178°和175°兩種彈道傾角情況下，對基于ADP的微分對策制導律和基于OSMG的制導律進行對比仿真，相應攔截軌跡和攔截過載結果如圖3～圖6所示。在目標彈道傾角為178°時，基于ADP的微分對策制導律與基于OSMG的制導律攔截效果均較為理想，不僅指令過載較小，且攔截精度較高。但是，當抬高目標初始彈道傾角到175°時，攔截效果出現了較大差異。

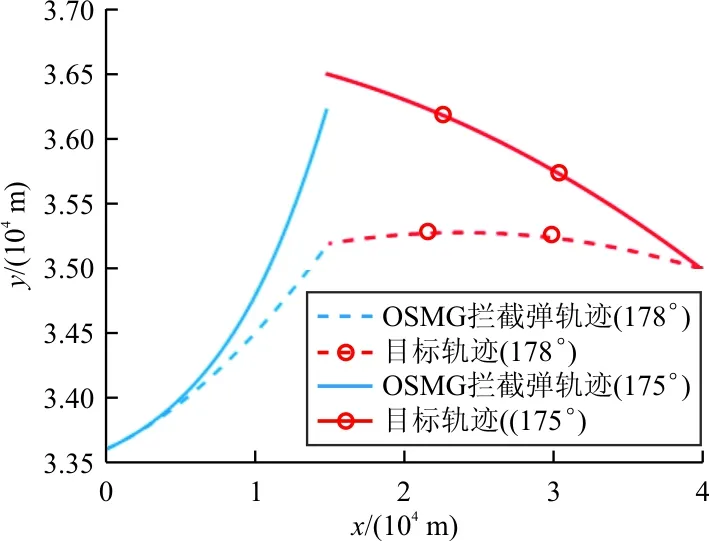
圖3 OSMG制導律在兩種情境下的攔截軌跡

圖4 OSMG制導律在兩種情境下的攔截過載

圖5 ADP微分對策制導律在兩種情況下的攔截軌跡

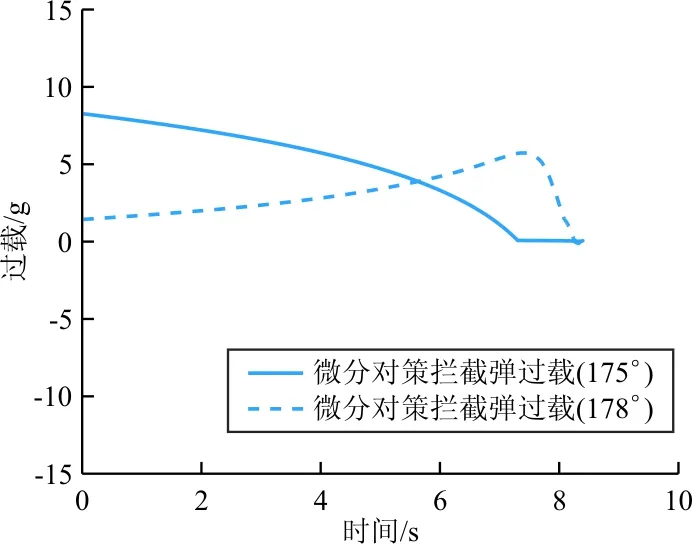
圖6 ADP微分對策制導律在兩種情況下的攔截過載

從圖3可以看出：當目標初始彈道傾角較大時，迎頭攔截趨勢較好，攔截效果也較好；當目標初始彈道傾角減小時，彈目間迎頭誤差較大，攔截彈需要進行較大程度的修正。但是由于OSMG這種基于視線角速度的比例導引律類制導律，初始視線角速度較小的情況下，修正較慢(過載指令小)，當與目標逐漸接近時，逐漸提升過載，但由于時機較晚，過載即使飽和(過載已經達到了10g飽和，如圖4所示)，也無法實現對目標的攔截。

基于ADP的微分對策制導律受到目標彈道傾角影響較小，適應性更好。從圖 5可以看出：不論目標初始彈道傾角是175°或是178°，均對目標實現了較好的攔截。從圖 6可以看出：當目標彈道傾角減小時，初始對準誤差較大，基于ADP的微分對策制導律采用較大過載實現了指向調整；隨后，攔截彈過載指令逐漸減小，直至攔截碰撞前收斂至0附近，這是因為基于ADP的微分對策制導律選擇了預測零控脫靶量進行設計的，當預測零控脫靶量較小時，攔截彈不再進行機動來實現對目標的攔截。

綜上所述，本文設計的基于自適應動態規劃的微分對策制導律能夠較好地實現對高超聲速目標的攔截，并且對于初始迎頭態勢要求不高，適應性更好。

4 結 論

(1) 本文針對具有博弈突防能力的高超聲速目標設計了一種基于自適應動態規劃算法的微分對策制導律，這種制導方法能夠快速便捷地對微分對策問題的納什均衡解進行學習。

(2) 所提出的方法能夠很好地實現對高超聲速目標的攔截。相較于最優滑模制導律，該方法的適應性更強，攔截效果更好。