靜電場對壓電薄膜中聲表面波傳播的影響
劉智榮,謝立強,朱 敏,包文歧
(陸軍工程大學 國防工程學院, 江蘇 南京 210007)
0 引言
聲表面波(SAW)技術發展至今,在傳感器和信號處理器上已得到了廣泛的應用[1-3]。當外電場作用到SAW傳播的壓電介質上時,由于逆壓電效應,會導致壓電介質內部產生應力和形變,進而影響SAW的傳播特性,因此,SAW可實現靜電場的感測。用SAW實現靜電場的感測,可有效解決現有電場傳感器干擾抑制能力差,不能無失真感測的難題[4-5]。
要實現SAW對靜電場的感測,首先必須探尋靜電場與SAW傳播之間的規律。Boris D. Zaitsev等[6]最早從壓電材料彈性常數變化的角度,研究了外加電場對鈮酸鋰中瑞利波相速度的影響。Zhang R等[7]研究了具有初始應力的磁電彈性半空間中瑞利波的傳播行為,得到了不同電、磁邊界條件下波速的解析解。D. Koulova等[8]通過實驗的方式研究了電場作用下絕緣液-空氣界面上波的傳播行為,分析了波長和角頻率隨電場變化的規律。
關于靜電場對壓電薄膜上SAW傳播的影響機理,目前國內外的研究較少。為此,本文在靜電場導致壓電薄膜產生初應力和形變的基礎上,利用小幅波動理論建立和求解了波動方程,并通過仿真分析討論了兩種壓電薄膜材料SAW在靜電場影響下的相速度變化和頻散曲線。
1 波動方程的建立
1.1 初始條件
圖1為一靜置于靜電場(E)中的無限大橫觀各向同性壓電薄膜,其厚為h,極化方向沿著z軸,坐標平面xOy與壓電薄膜的中面重合。E方向沿著壓電薄膜的極化方向。

圖1 靜電場中的壓電薄膜
根據假設條件,可由壓電本構方程得到靜電場作用下壓電薄膜中的初始應力和初始電位移為
(1)
式中:c13、c33為壓電薄膜的彈性常數;e31、e33為壓電系數;ε33為介電常數。
1.2 波動方程
研究了靜電場對壓電薄膜SAW傳播行為的影響,即在波動分析中考慮靜電場作用下的初始應力和初始電位移。具有初始應力和初始電位移的壓電介質小幅波動問題的運動方程[9-11]為
(2)

若SAW沿x方向傳播,則壓電薄膜中質點的機械位移u=u(x,z,t)、v=0、w=w(x,z,t)和電勢函數φ=φ(x,z,t)。于是式(2)可化簡為
(3)
由于波傳播與y方向無關,因此,壓電薄膜的本構方程為
(4)

將式(1)、(4)代入式(3)中,得到由機械位移分量及電勢函數表示的波動微分方程:

(5)
2 波動方程的建立
設壓電薄膜中質點的u、w和φ的解分別為
(6)
式中:c為SAW相速度;k=2π/λ為波數,λ為SAW波長;a為待定系數;A1、A2、A3分別為u、w、φ的幅值。
1.4 觀察指標 比較兩組患者治療后的臨床有效率,以及治療前后裸眼視力、血糖相關指標(空腹血糖、餐后2 h血糖、糖化血紅蛋白)、血液流變學相關指標(血漿黏度、紅細胞聚集指數、紅細胞變形指數)、血清相關因子(血管內皮生長因子、低氧誘導因子-1α)等水平變化。
將式(6)代入式(5)中,有
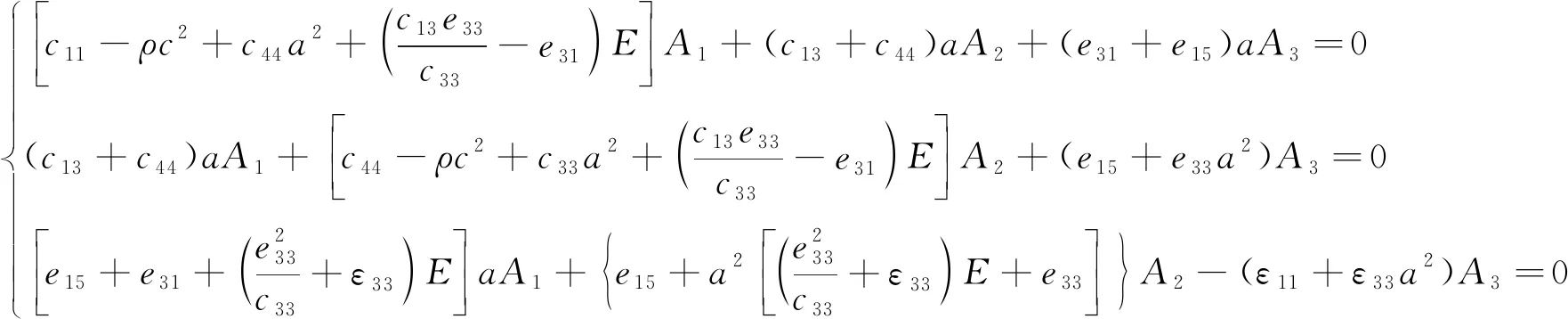
(7)
要使式(7)有非平凡解,須使其系數行列式等于0,且該行列式可看成是以c及E為參數、a為未知量的1個6階代數方程。由于z→時,SAW的位移衰減至0,因此,a僅取虛部為正的3個根,記為an(n=1,2,3)。式(7)可表示為
(8)
其中

(9)
(10)
壓電薄膜的上、下表面外力自由,且可視為電學短路,因此,邊界條件有
(11)
故壓電薄膜的位移和電勢函數的完整解應為
(12)
(13)
其中Q為3階方陣,其元素Qpn(p=1,2,3;n=1,2,3)為
Q1n=(c13+c33fnan+e33gnan)e±ikanh/2
(14)
Q2n=(c44an+c44fn+e15gn)e±ikanh/2
(15)
Q3n=gne±ikanh/2
(16)
為使A有非平凡解,則有
|Q|=0
(17)
式(17)即為SAW的相速度或頻散方程。
3 仿真分析及討論
本文選用氧化鋅(ZnO)和氮化鋁(AlN)這兩種壓電薄膜材料,分析其SAW傳播特性。這兩種材料的性能參數如表1所示。

表1 壓電材料相關參數
設定E=0~10 kV/mm。設m=h/λ為壓電薄膜厚度與SAW波長之比(厚波比),當m=1、2、5、10時,通過仿真可得c與E關系如圖2所示。由圖可知,無論m取何值,兩種材料中的c都隨E的增加而線性增加,其中ZnO和AlN相速度曲線斜率


圖2 ZnO、AlN材料中c與E的關系
分別為0.106和0.117,可見ZnO和AlN材料中SAW對E的敏感度相當。盡管m取值不同,但曲線幾乎重疊,符合c與壓電薄膜材料的物理尺寸無關,但與彈性性質、壓電性質及介電特性有關的研究理論[12]。
圖3為在不同E的作用下,h=0.1 mm時ZnO和AlN所對應的頻散曲線。由圖可知,在E的作用下,SAW傳播的c在波數較低(k<2×105/m)時變化明顯,由λ=2π/k可得,即當λ>31.4 μm時,SAW對E的變化更敏感。在k→,即波頻率f=kc/2π非常高時,c逐漸平穩并趨向于剪切體波波速,此時E對c的影響較小。此外還可發現,在同一波數下,E越大,對應的c越小。

圖3 靜電場作用下ZnO、AlN材料的頻散曲線
這一物理現象本質是靜電場作用下,由于逆壓電效應,壓電薄膜內部產生了應力場和電位移場,使SAW的傳播行為受到影響。綜上可知,只需要測量出c的實際值,便可得出對應靜電場值,這可以作為測量靜電場大小的一種方法。
4 結束語
本文得到了靜電場作用下聲表面波在壓電薄膜中傳播的相速度變化及頻散曲線。在壓電薄膜材料參數給定的情況下,靜電場值越大,聲表面波的相速度越大。波數越小,聲表面波對靜電場的變化越敏感;波數越大,即頻率越高時,聲表面波的相速度越小。因此,通過對聲表面波相速度的測量可以確定外加靜電場值的大小。

