基于區間二型T-S模糊系統的壓電遲滯特性建模

陳圣鑫，趙新龍,蘇 強，蘇良才

(浙江理工大學 機械與自動控制學院，浙江 杭州 310018)

0 引言

壓電驅動器作為一種可以將電能轉化為機械運動的微位移元件，由于其體積小，精度高等特點被廣泛應用于超精密系統中。但是，其固有的遲滯特性會降低精密系統中的控制精度，甚至影響系統的穩定性[1-3]，故而需要對遲滯進行建模。Takagi-Sugeno(T-S)模糊模型因其結構簡單、辨識精度高的特點而被廣泛應用于復雜非線性系統的建模[4-6]。T-S模型的結構辨識主要包括模糊區間的劃分、模糊前件參數和后件參數辨識。

在模糊區間劃分方面，模糊聚類算法得到了廣泛應用，主要有模糊C均值(FCM)聚類算法和模糊C回歸模型(FCRM)聚類算法等。其中，FCM聚類算法作為以歐氏距離為依據進行區間劃分的方法，更適用于超球型的模型結構。FCRM聚類算法作為一種超平面型聚類算法，其迭代產生的超平面與T-S模糊模型的子模型有相似的結構， FCRM聚類算法更適合于T-S模型模糊區間的劃分。KUNG等[7]提出了FCRM聚類算法的有效性準則，用來選擇合適的聚類個數，但對于給定的壓電輸入信號來說，所需劃分的聚類個數有限，并不需要有效性準則的判斷。CHANG等[8]使用垂直距離公式替換了傳統聚類算法的誤差公式，使聚類劃分更準確，但并未進一步考慮聚類算法和模型的結構匹配問題。在模糊前件參數辨識方面，LI等[9]提出了新的超平面型隸屬度函數，解決了傳統超球面鐘型高斯函數與超平面型FCRM聚類算法結構不匹配的問題。在后件參數辨識方面，利用最小二乘法來完成模糊后件參數的辨識。

基于一型模糊集的T-S模糊系統已用于復雜非線性系統建模[10-11]，但是一型模糊集的隸屬度值是清晰的，在處理不確定性方面存在局限性[12-14]。區間二型模糊集通過將隸屬度由清晰值擴展到一個區間值，把隸屬度進一步模糊化，可以更有效地處理系統的不確定性和非線性[15-17]。

本文基于文獻[18]提出的區間二型FCRM聚類算法，用垂直距離更新了算法中的誤差計算[8]，提出了改進的區間二型FCRM聚類算法。引入超平面隸屬度函數[9]，解決了超球型高斯隸屬度函數與改進超平面型聚類算法的結構不匹配的問題。與其他建模方法相比，本文的創新點是：

1) 用垂直距離公式替換了傳統FCRM聚類算法的誤差公式，使聚類算法與其所辨識的超平面結果直接相關聯，提高了模糊區間劃分精度。

2) 用超平面隸屬度函數替換了傳統的超球型高斯隸屬度函數，使其與改進超平面型聚類算法的結構相匹配，提高了建模精度。

1 基于區間二型T-S模糊模型的壓電遲滯特性建模

1.1 壓電驅動器遲滯建模

區間二型T-S模糊模型的結構辨識過程如下：

2) 結合模糊隸屬度函數進行模糊模型前件參數的辨識。

3) 利用最小二乘法進行模糊模型后件參數的辨識。

1.2 區間二型T-S模糊模型辨識

1.2.1 模糊空間劃分

假設將n個數據(xk,yk)(k=2,…,n)劃分為c個聚類，則每個聚類中的數據樣本都符合一個線性回歸模型，該模型實際上是一個超平面回歸函數，其中第i(i=1,…,c)個超平面可表示為

(1)

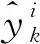
為了匹配二型模糊區間的上、下隸屬度，引用上、下超平面的形式[18]。利用加權最小二乘法，得到上、下超平面系數：

(2)

(3)

其中

(4)

Y=[yk](n-1)×1

(5)

(6)

(7)

降型得超平面系數[18]：

(8)

為了使聚類劃分更精確，引入了垂直距離公式[8]：

(9)

式中dik(Qi)為xk到第i個超平面的垂直距離。

(10)

(11)

式中：m1,m2∈(1,)且m1≠m2；U=[uik]c×(n-1)為模糊劃分矩陣；uik∈[0,1]為第k組數據隸屬于第i個超平面的隸屬度。

利用拉格朗日乘子法，式(10)、(11)可寫為

(12)

(13)

式中：λk為拉格朗日乘子；L1(U,λ)和L2(U,λ)分別對λk和uik求偏導，得到uik的最優值：

(14)

(15)

(16)

(17)

降型得隸屬度uik的精確值[18]：

(18)

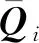
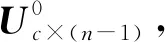
步驟4：通過式(18)得到uik，得到新的模糊劃分矩陣Ur+1=[uik]c×(n-1)。

步驟5：比較Ur和Ur+1，如果滿足‖Ur-Ur+1‖≤ε，迭代結束；否則，r=r+1，重復步驟2～5。

引用式(9)替代了文獻[18]中的誤差計算公式，通過使聚類算法與其所辨識的超平面結果直接相關聯，使聚類的劃分更精確。

1.2.2 前件參數辨識

鐘型高斯函數作為超球面隸屬度函數，具有明確的聚類中心和寬度，與本文所提超平面聚類算法結構不符。本文采用超平面隸屬度函數[9]，則輸入xk對應第i個模糊集合Bi的上、下模糊隸屬度函數為

(19)

(20)

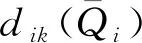
第i條規則的激活強度ωi(xk)為

(21)

輸入xk對應的區間二型T-S模糊模型的輸出如下：

(22)

1.2.3 后件參數辨識

確定了模糊前件，可以通過下式得到模糊后件參數：

y=A·θ

(23)

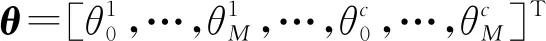
(24)

其中

(25)

(26)

在本文中，利用最小二乘法來辨識式(23)中的θ為

θ=(ATA)-1XTy

(27)

2 實驗與仿真

整個實驗平臺由壓電驅動器(PZT-752.21C)、 dSPACE DS1103、電壓放大模塊(E-505.00)、傳感器模塊(E-509.C1A)、控制臺組成，用于實驗數據的采集，實驗平臺如圖1所示。然后針對10 Hz、50 Hz、100 Hz正弦輸入進行模型驗證。最后在正弦衰減輸入下，與文獻[10]中的建模方案進行對比。

圖1 實驗平臺

輸入信號為x(t)=0.1sin(2πft)，輸入頻率f=10 Hz、50 Hz、100 Hz，給定參數τ=4，c=5，m1=1.7，m2=3.3，ε=0.001。

圖2～4為f=10 Hz、50 Hz、100 Hz時模型輸出與實際輸出曲線。圖5～7為f=10 Hz、50 Hz、100 Hz時的誤差曲線。表1為不同輸入頻率下的模型誤差。

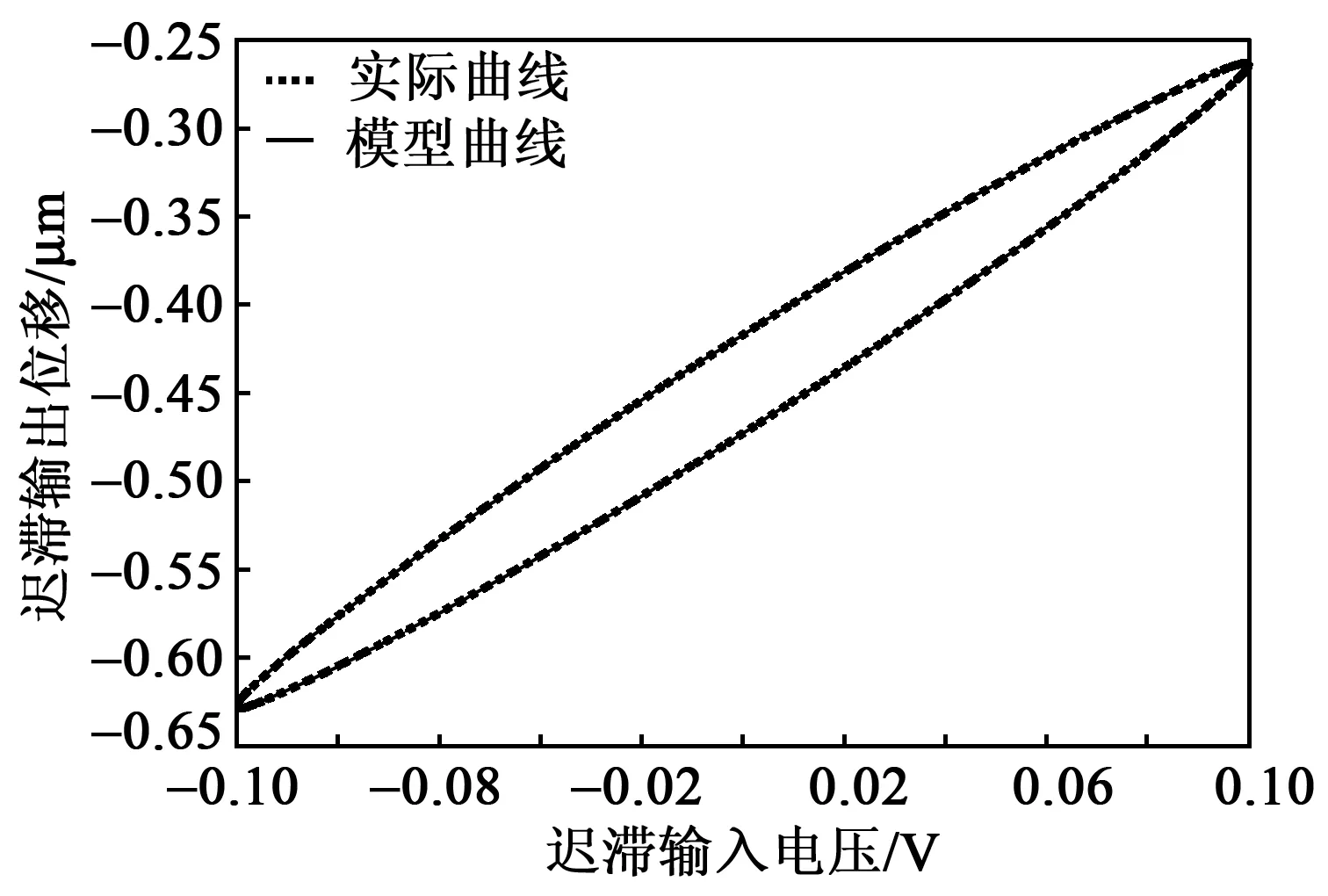
圖2 f=10 Hz時實際與模型輸出曲線

圖3 f=50 Hz時實際與模型輸出曲線

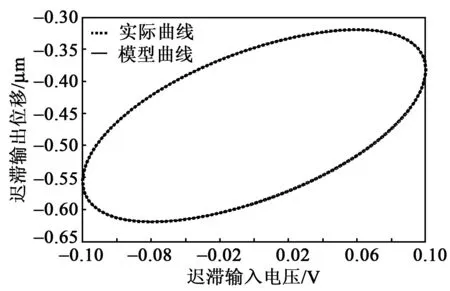
圖4 f=100 Hz時實際與模型輸出曲線

圖5 f=10 Hz時實際模型誤差曲線

圖6 f=50 Hz時實際模型誤差曲線

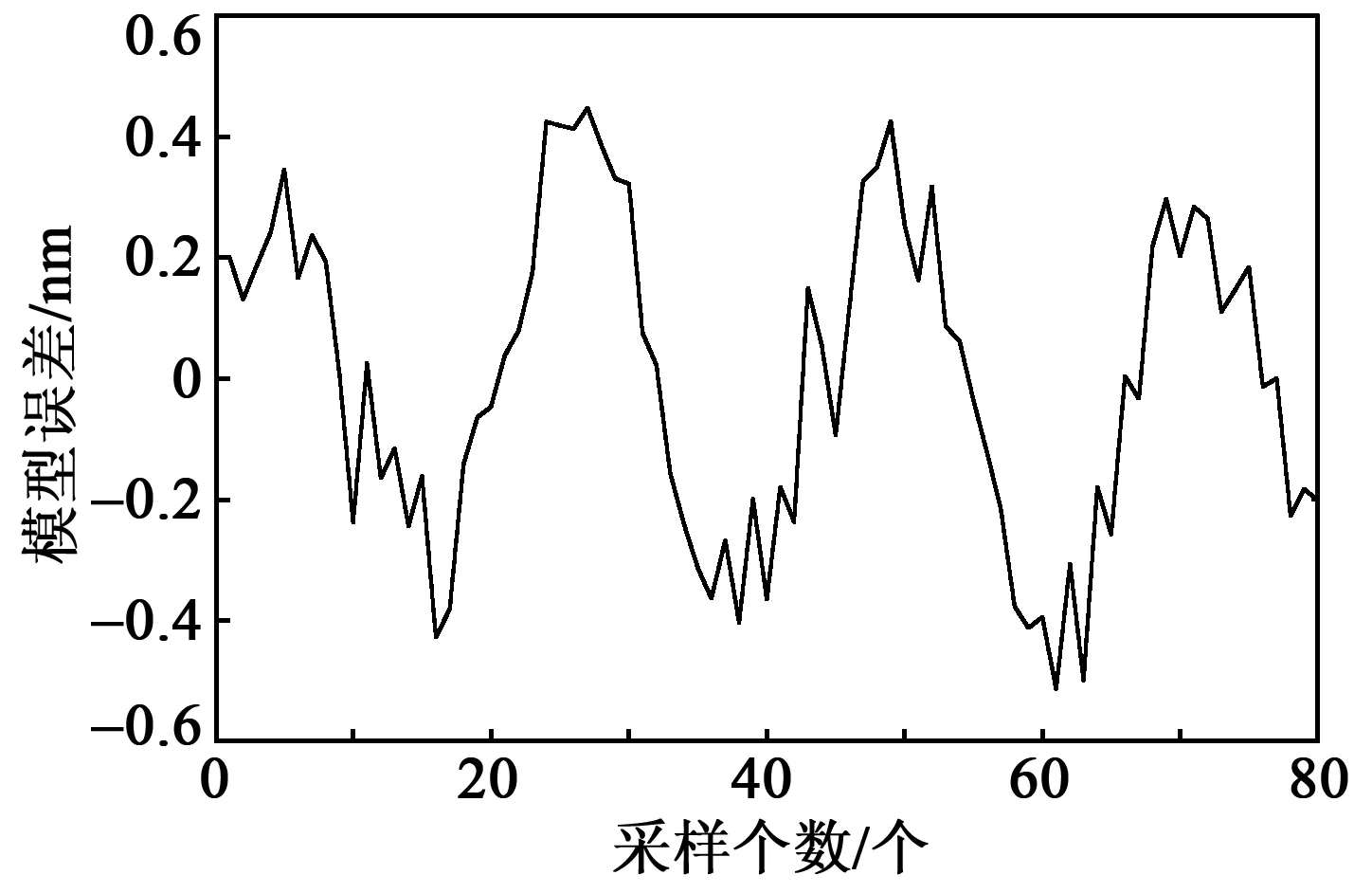
圖7 f=100 Hz時實際模型誤差曲線

表1 不同輸入頻率下的模型誤差

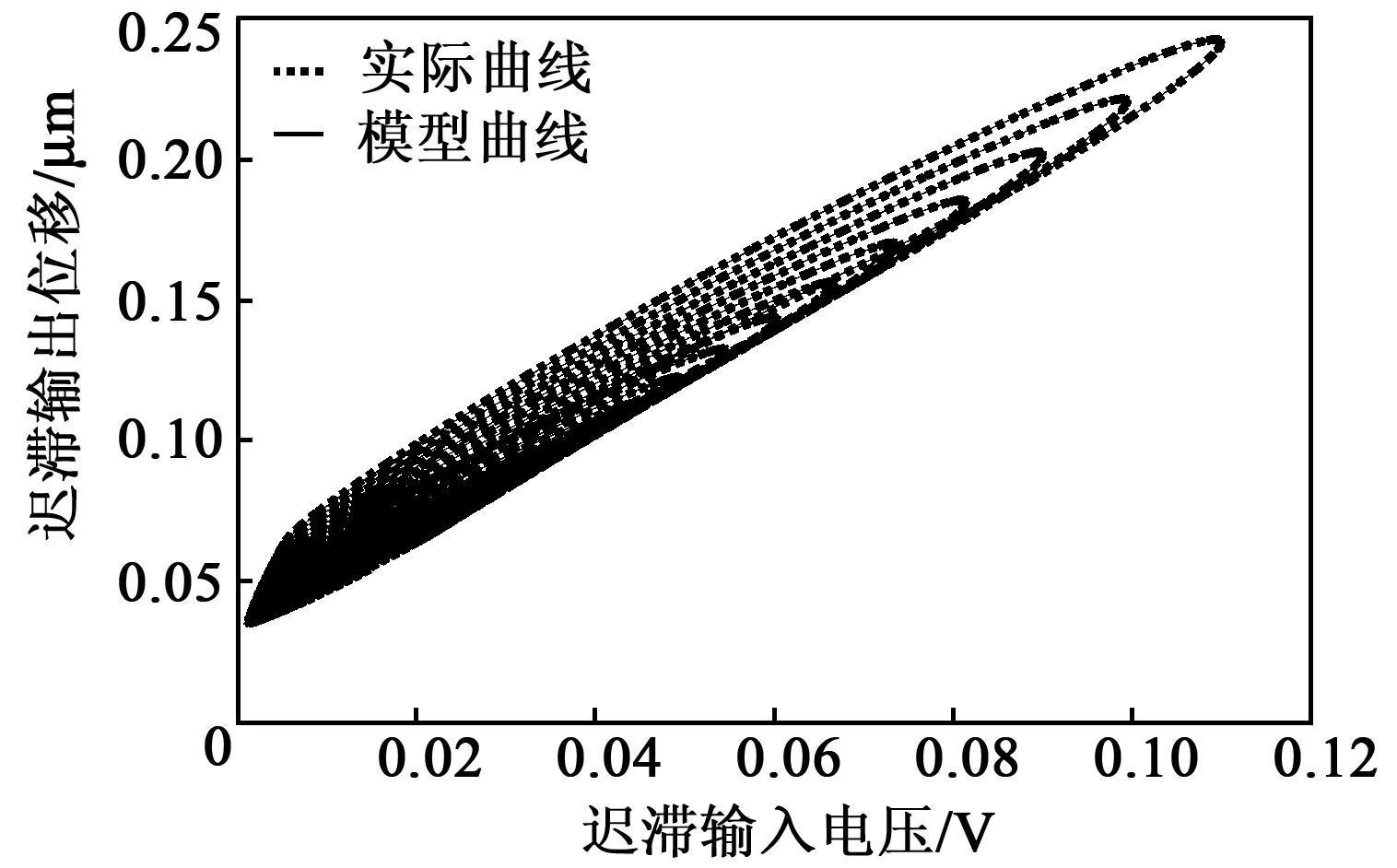
圖8 實際輸出與模型輸出曲線

為了驗證該模型的辨識精度，選擇超球面型隸屬度函數的建模方案作為對比。在正弦衰減輸入信號作用下，均采用三輸入-單輸出的模型結構，將本文模型與文獻[10]中的建模方案進行比較。輸出曲線及誤差曲線對比分別如圖8、9所示。模型對比如表2所示。

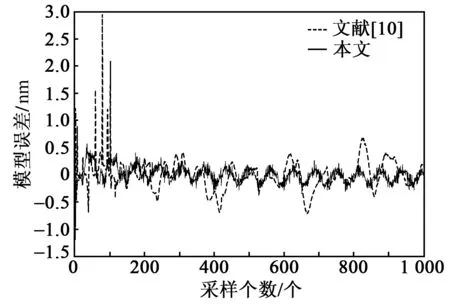
圖9 本文與文獻[10]建模誤差對比

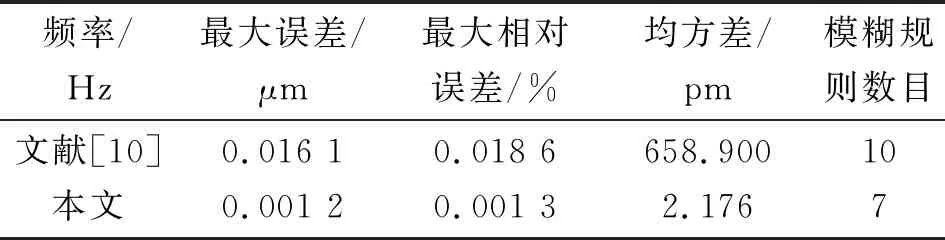
表2 本文與文獻[10]模型參數對比

3 結束語

本文建立了壓電驅動器遲滯特性的區間二型T-S模糊模型。引用垂直距離公式替代了傳統的誤差公式，提出了改進的區間二型FCRM聚類算法用于模型的結構辨識，并引入了與該超平面型聚類算法結構相匹配的超平面隸屬度函數，提高了建模精度。實驗結果表明，該建模方案可以有效地辨識壓電驅動器的遲滯特性。