讓思維在小學數學課堂馳騁
——小學數學教學中思維力培養策略分析

胡 薇

(江蘇省徐州市玉潭實驗學校 221000)

思維是數學的靈魂，思維力的培養是數學教學的中心任務，是學生綜合發展的基本要求.目前的教學實踐中，教師們更多關注教材的講授、知識的灌輸，忽視能力的培養，忽視思維力的培養.思維是數學的主要特點，忽視思維力的培養，數學教學也失去了生命力.因此，在素質教育的今天，探討思維力的培養，是數學教學教學實踐中，不得忽視的問題.下面，結合教學實踐，對于小學數學教學中，培養思維力的方法和策略問題進行論述.

一、重視說理訓練，發展學生思維力

數學課堂應該是“講理”的地方.“說理”的過程，也是概念清晰、公式由來明晰、思維發展的過程.學生在“說理”的過程中，思維清晰、語言表達有條理、獲得成功的體驗，萌發學習的興趣.為此，數學課堂教學中，應重視“說理”訓練，讓數學課堂因“說理”而有效，因“說理”而精彩.

任何知識都有一個發生發展的過程，數學知識也不例外.數學課堂中，讓學生將知識的由來和過程“說”清楚，這個“說”清楚的過程，需要學生嚴謹的思維力、流暢的語言能力.“說理”也可以讓學生發現學習中的不足、快速認識到出現的錯誤，利于學生查漏補缺.

如《分數乘分數》的教學時，對于教材例4：涂色部分表示一張紙的二分之一，斜線部分各占1/2的幾分之幾？各是一張紙的幾分之幾？

這個問題情境的給出，借助于圖例，學生很快發現斜線部分占1/2的1/4，是整張紙的1/2×1/4，并對計算的過程說出來.這個過程，讓學生掌握了分數乘分數的意義——表示求一個分數的幾分之幾、以及分數乘分數的計算方法——分子與分子相乘作分子、分母與分母相乘作分母.整個過程，無容置疑，學生的思維力、探究學習能力、語言能力都得到發展，學生也因知識的構建而收獲學習的快樂.

“說理”也包括公式的推導過程.如“三角形面積的計算”，讓學生說說如何推導出三角形面積公式：底乘高除以2等；“說理”，也包括說出問題的解題思路，如簡便運算98×66+2×66，讓學生說出簡便運算時，運用的什么運算律.“說理”的過程，是學生思考問題、解決問題的過程，有助于學生思維力的發展.

再者，學生在計算時，難免出現錯誤.此時，教師讓其說“理”，學生在“說理”的過程中，會自主發現解決問題時，出現的不足，立刻意識到錯誤所在.如“比的認識”的教學時，對于填空題5∶8=30∶( )，不少學生填上8.對于這個結果，教師改變簡單的對錯的評價方式，而是讓學生自主說出方法——比的前項擴大為6倍，后項也擴大為6倍.此時，迅速發現自己的錯誤，及時彌補不足.

再如五年級的《找規律》的教學，可以設計“組學”的任務：你能用數學的眼光去發現花盆、彩燈、彩旗擺放的規律嗎？

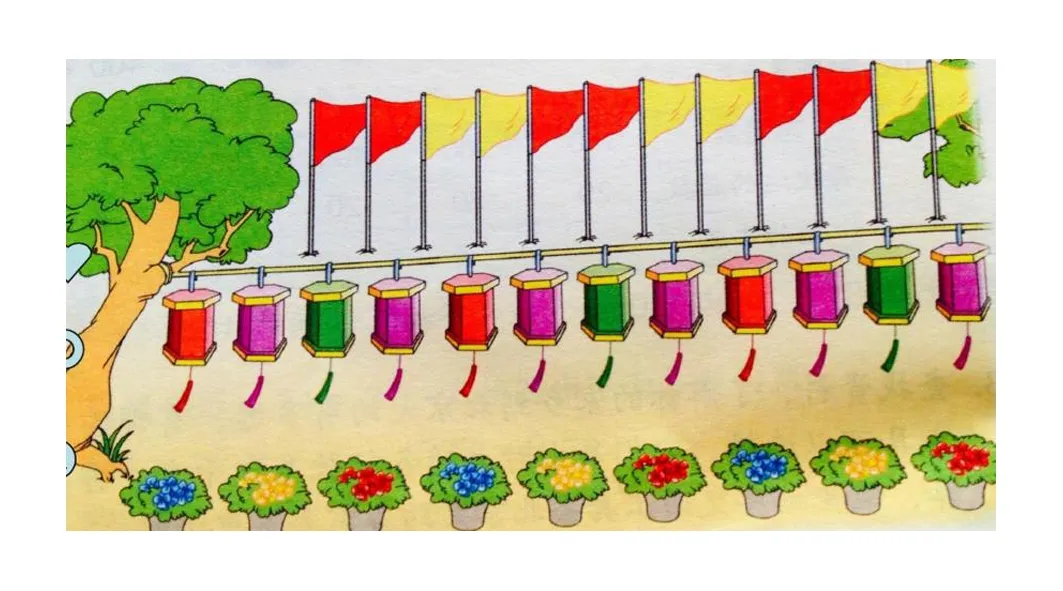
任務提出后，給學生留出思考、探討的時間，教師也可以以其中的一個作為例子進行方法的提示，如盆花的擺放問題為例，幫助學生找出擺放的順序問題：

教師進一步引導學生說紅旗的排放順序是每( )面一組，每一組的排列順序都____(相同、不同)，排列順序是____、____、____、____.彩燈的每( )個一組，每一組的排列順序是____、____、____、____.

“說理”是思維力發展的重要手段，對于學習意義重大，教學中，教師應引導學生學會說理，讓思維在說理過程中綻放，提升學生綜合能力.

二、適當融入難題，提升學生思維力

教學實踐中不難發現，平時的期中、期末考試，以后的小升初、中考、高考等，拉開分數段距離的不是基礎題，而是靈活性、難度系數較大的問題.這些題，之所以容易拉開距離，主要是多數學生對于這類題倍感難度，從內心深處，對這些難度較大的題，有抵觸和畏難情緒.為此，平時的教學中，就應該適當融入難度較大的問題，通過難題的思考和探究，提高學生的思維力.

如《平均數》的教學時，練習一般設計為給出一組數據，讓計算出平均數，這樣的練習，純粹是“求和再除以數據的個數”的方法的運用，無濟于思維力的培養和發展.而教師如果涉及思考題：數學測驗，第一小組6個人的平均成績是90，如果一個學生的成績改為98，可使小組平均分提高了1.5分，那么，這個學生的原來分數是多少？顯然，這個問題，靈活性較大，利于發展學生的變式思維，提高學生的創新解決問題的能力.

融入難度較大的問題，應在學生的最近發展區之內.否則，難度太大，也會讓學生望而生畏.如《分數四則混合運算》的教學時，教師可以給出難度稍大的問題，通過問題的分析和解決，培養學生分析問題、解決問題的能力.如根據條件，補全問題，再解決問題.如：有兩根繩子，第一根長2/3米，____，第二根繩子長多少米？(1)2/3×1/3：____；(2)2/3×(1+1/3)：____.這類問題，需要學生根據列的算式，而補充條件，這類問題，與常規的練習題的思維方式，可以有效培養學生的變式思維能力，培養創新思維能力.

數學教學中，經常性融入一題多解題、奧數題等，培養學生的思維力，也培養學生克服困難、戰勝困難的信心，從而促進學生的全面發展.

三、融入實踐活動，培養學生做中思

實踐性是數學的主要特點，數學源于生活、運用于生活.數學教學中，教師應根據學科特點，根據小學生活潑、好動、好奇的特點，融入操縱性的實踐活動，讓學生在“做中思”、“思中做”.

如教學“百分數的認識”時，開展“生活中的數學”的尋找活動.如讓學生借助于相關的資料，查詢空氣中的氧氣、氮氣、二氧化碳等的含量，并分析這些數據的意義；班級期中考試后，成績分析中，優秀(成績90分以上)率12%；衣服上的百分數：面料100%棉；啤酒的酒精度是3.8%；套圈命中率是55%；郵政存款年利率是2.25%…通過尋找生活中的百分數的活動，學生意識到生活中處處有數學、數學中也無處不生活.

尋找生活中的數學的活動的開展，應滲透到教學的各個章節中.通過生活中的數學的尋找，分析生活中的數學的意義、特征，從而有助于數學知識的學習和鞏固，促學生且行且思，發展學生的能力.如《長方體和正方體》的教學時，讓學生尋找生活中的長方體和正方體，通過尋找到的長方體、正方體的實物，細心觀察，分析其主要特點.如借助于尋找到的鞋盒子，觀察鞋盒的六個面的特點、找出12條棱的特點，這樣，實現“做中思”、“思中做”，也實現“教學做合一”，更實現“學以致用”.

再者，創設生動的情境，也是培養學生思維力的主要方法，通過生動的情境，激發學生探究的欲望，促學生積極思維.如“分數的意義”的教學時，借助于麗麗過生日，淘淘為麗麗慶祝生日的情境，然后，根據情境提出問題：麗麗和淘淘平均分吃一塊蛋糕，一人吃蛋糕的多少？從而引出“一半就是1/2”的概念，引發學生對1/2的意義的理解和思考，從“分蛋糕”的情境，引出抽象的數學概念，從形象到抽象，學生的思維力不斷提升.

總之，培養學生的思維能力的方法很多,教學中，教師應改變傳統的重知識的方法，運用新方法，從情景的創設、問題的設計、難題的運用、實踐活動的開展等，為學生思維力的培養和發展提供機會，讓思維滲透到數學學習的全過程，在數學課堂上馳騁，促數學教學更有效.