筒子紗包裝自動配重方法研究

彭來湖，祝孝裕，張少民，胡旭東

(1. 浙江理工大學 浙江省現代紡織裝備技術重點實驗室，浙江 杭州 310018； 2. 海寧紡織機械有限公司，浙江 海寧 314400)

國內外紡紗企業生產的最終產品是紗線，無論何種顏色的紗線以及何種生產方式，其大都以筒子紗的形式出售[1]。筒子紗是紡織行業絡筒工序的產出品，是從上道工序的細紗機或捻線機上落下來的管紗，根據機織或針織等后道工序的用紗要求，使紗線長度接長并清除紗線上疵點和雜質，在絡筒機上通過急行往復的導紗鉤或槽筒重新卷繞成無邊或有邊的、具有一定形狀(如圓錐形)、一定卷繞密度、較大體積的筒子紗[2]。筒子紗用來生產布匹、針織品或毛巾等相關產品，一般為圓錐形，其直徑大約在120～260 mm之間，大端與小端的直徑差在10 mm以內，紗線高度比管筒略低，高度在150～180 mm之間[3]。

目前，筒子紗的收集、套袋、配重、打包等包裝過程大都由人工進行，工作量大，長期重復勞動易產生疲勞，且效率低下。在企業用工急缺的情況下，筒子紗的包裝成為了亟待解決的問題[4]。國外的諾茵豪斯(Neuenhauser)公司推出了筒子紗的自動化包裝系統[5]，可以按筒子紗的品種進行分揀、打包。但其占地面積大，而且包裝筒子紗需要大量的托盤，最重要的是沒有進行筒子紗的配重。國內的企業和科研單位也進行了筒子紗包裝系統的研究，其中琿業公司生產的筒子紗包裝系統自動化程度不高，實際沒有提高生產效率。青島環球集團生產的筒子紗包裝系統直接與絡筒機連接，采用懸掛式的運送方式，成本較高，并且缺少配重環節。山東康平納公司研發的筒子紗包裝系統可以對筒子紗進行大小頭檢測并翻轉，但缺少筒子紗的配重環節。很多學者也對筒子紗的包裝系統做了相關的研究，其中謝楠等[6]設計了分布式筒子紗包裝與碼垛控制系統，該系統擁有自動取紗、輸送、包裝和碼垛裝置，但也缺少筒子紗配重裝置。楊偉[7]對筒子紗自動輸送系統進行了研究，可以對多個品種的筒子紗進行分揀、輸送，進行大小頭翻轉等，不足的是同樣缺少配重環節。李瑞琴等[4]在軟件上實現了筒子紗的自動包裝，并沒有做出實際產品，最重要的是沒有對筒子紗進行配重處理。

這些紡紗企業研發半自動化包裝生產線，以實現對筒子紗的自動收集、套袋、打包，減少了用工，也提高了筒子紗包裝的效率，但其中缺少最重要的配重環節。由于國內大部分紡紗企業采用國產絡筒機，絡出來的筒子紗其品質參差不齊，直徑不均勻，質量相差較大，因此，目前市場上已有的機械化打包裝置不適用于此類筒子紗的自動包裝。針對以上問題，本文結合自動配重包裝工藝設計了總體方案，對儲紗原理及配重機制進行深入研究，設計了3種配重方案，通過仿真對比測試，采用區間分布及質量配對法高效、節時。經過大量生產實踐表明，采用本文研究的自動配重方案節省了勞動力，降低了企業成本的同時增加了配重效率，減少了配重時間，增加了企業的效益。

1 總體方案設計

圓錐形筒子紗打包時，紗筒與紗筒間需要盡量減少空隙，因此相連紗筒需要正反間隔排布；包裝袋內紗筒的排布規律主要是三乘四，每袋質量誤差控制在60 g以內。根據以上要求，設計筒子紗自動包裝流水線主要由放筒運輸線、動態稱重分管道輸送線、儲紗立體庫、配重組合線、翻筒包裝線組成。針對各條生產線的控制需求，本文提出了一種筒子紗自動配重包裝的包裝流水線控制系統設計方案，軟、硬件采用模塊化的結構以適應筒子紗自動配重包裝的需求[7]。圖1示出了筒子紗自動配重包裝系統方案的總體原理圖。

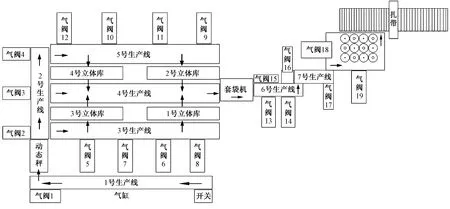
圖1 筒子紗自動配重包裝系統結構原理圖Fig.1 Structural schematic diagram of automatic cheese weight packing system

該系統的最大特點是通過自動配重算法實現筒子紗的稱量、配重、套塑料薄膜、打包一體化。如圖2所示，動態秤獲得運動過程中筒子紗的質量信號，傳輸給主機實際筒子紗的質量，再根據當前是起始儲紗模式還是實際配重模式的相應算法進行筒子紗的存儲或配重。若是實際配重模式則執行后續的套袋、選擇性翻轉、打包等工作。起始儲紗模式是開機時判斷立體庫中存儲的筒子紗個數是否滿足實際規定的個數，在不滿足的情況下才進行筒子紗存儲。儲紗準備就緒時，則正式開始筒子紗的配重打包工作。當筒子紗滿足單個筒子紗質量范圍，則進行配重，通過算法判斷該筒子紗是否滿足實際配重需求：若滿足則進行后續的套袋、打包工作；若不滿足則再進行判斷是否能和立體庫中的筒子紗經過比較置換出滿足要求的筒子紗，若能尋找到合適的筒子紗，則置換出的筒子紗也進行后續的套袋、打包工作。在這個過程中所有不滿足的筒子紗從2號生產線流出整個系統。

圖2 筒子紗自動配重包裝系統控制流程圖Fig.2 Control flow chart of automatic cheese weight packing system

2 儲紗模式基本原理

在起始儲紗模式下，系統會讀取4個立體庫中已存筒子紗的個數K1，K2，K3，K4。立體庫有12個儲紗框架。設置儲紗個數為YN(YN≤12)，K1～K4在未達到YN時，則輸送的筒子紗要進入立體庫中儲存，直到每個立體庫中的筒子紗個數都達到YN個，儲紗完成，儲紗模式結束。

將設置的筒子紗的質量范圍平均分成輕、正常、重3個區間，在儲紗時將筒子紗按照這3個區間進行儲存，即一個立體庫中的儲紗情況要滿足輕、正常、重3個區間的筒子紗數量基本均衡，以保證立體庫中的筒子紗能滿足后續配重模式的置換工作。

現假設筒子紗都滿足設置的單個質量范圍，不滿足的會從2號生產線流出。若第1個筒子紗在輕區間，則先進1號立體庫，再判斷第2個筒子紗所在的質量區間。繼續進入1號立體庫，保證每個區間的個數不超過YN/3，若超過YN/3，則該筒子紗進入下一個立體庫。以此類推，保證每個立體庫的每個區間中在3個質量區間的筒子紗個數不超過YN/3個，這樣就認為4個立體庫中的筒子紗基本符合配重模式的要求。系統每次開機時都會自動檢測4個立體庫中的筒子紗個數，保證儲紗個數達到YN。

3 配重機制分析

3.1 配重目的

紡紗企業進行筒子紗配重就是從個體具有一定質量范圍的一系列筒子紗中找出給定個數筒子紗組成一包筒子紗，使其質量滿足[Yw-ε,Yw+ε]，Yw為一包筒子紗的設定質量，ε為配重精度，一般固定不變為60 g。

設單個筒子紗的質量范圍為[Wmin,Wmax]時，可判定為合格筒子紗，則：

根據紡紗企業的實際情況，現假設筒子紗的質量范圍在[1 700,2 300]區間內，每包筒子紗的質量為25 kg。

可見，當1包筒子紗在給定范圍內隨機抽取 12個時，總誤差高達1 kg，與規定的60 g相差甚遠，已經遠遠超過了配重的要求，而紡紗企業中采用人工配重方式，效率低下，因此，要研究如何實現快速穩定的筒子紗配重方法。

3.2 配重原理

筒子紗配重原理主要是已打包的筒子紗的質量加上當前正在計算的筒子紗和從4個立體庫中能找出的筒子紗，在質量上能達到[Yw-ε,Yw+ε]，Yw為25 kg，ε為60 g，在數量上能達到12個筒子紗，則認為當前的筒子紗滿足配重要求。

具體步驟如下，起始儲紗模式已準備就緒，進入實際配重模式，實際配重模式如圖3所示。

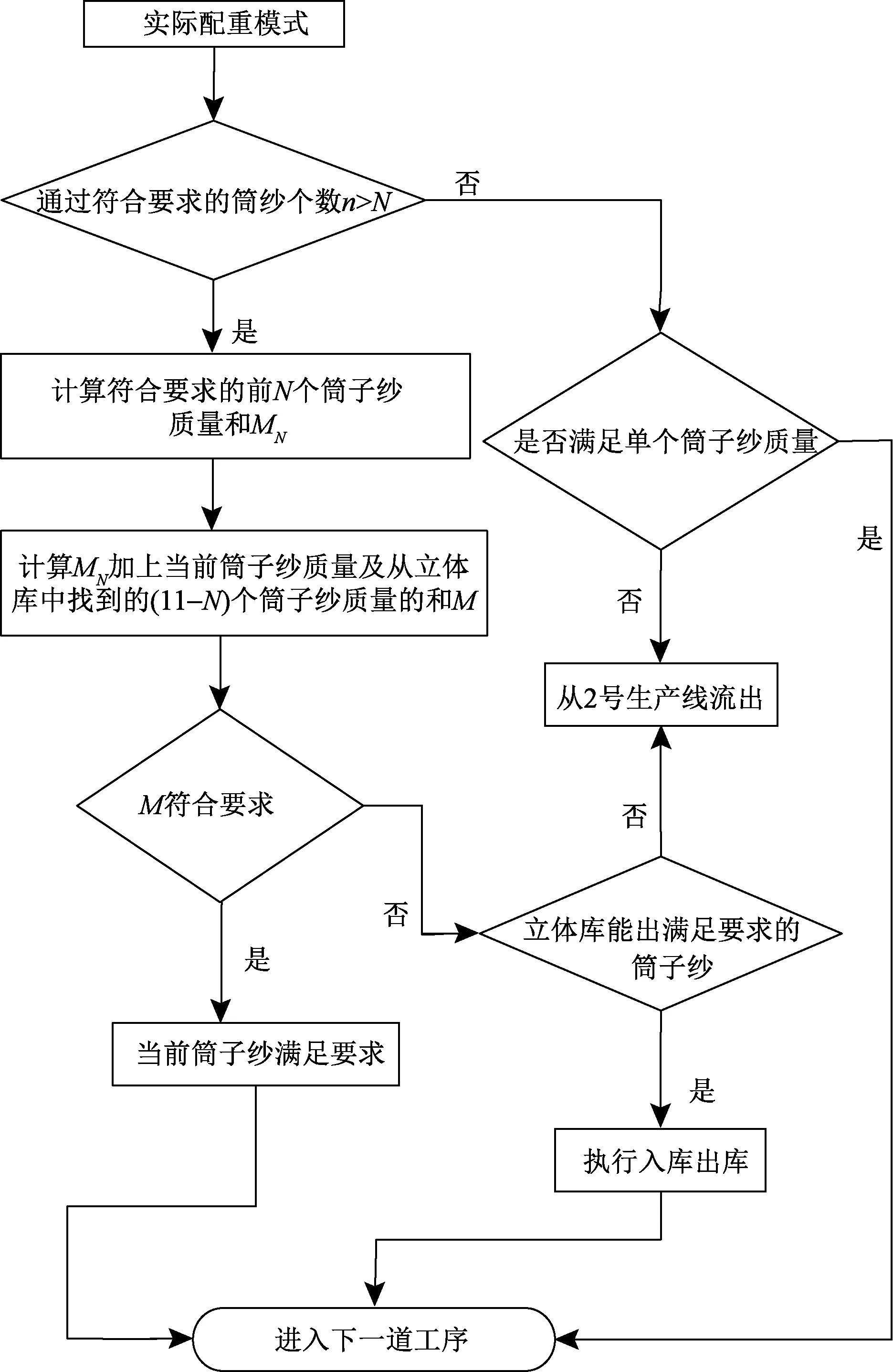
圖3 實際配重模式流程圖Fig.3 Actual counterweight mode flow chart

1) 當前一包的第1個筒子紗由1號生產線進入動態秤稱量(動態秤的誤差在2 g左右)，在滿足給定的單個筒子紗質量的條件下，直接從2號生產線進入4號生產線參與下一步執行動作，并記錄該筒子紗的質量。之后繼續進行第2個筒子紗的動作執行，一直到給定的N(N≤10，N越接近12則越難配重)個。這時已經有N個筒子紗在滿足單個筒子紗質量的條件下進入后續的包裝工序。

2) 當第N+1個筒子紗經過動態秤時，將這個筒子紗的質量傳給控制單元，先加上前面已經符合要求的N個筒子紗的質量和MN，然后從立體庫存儲的4YN個筒子紗中尋找(11-N)個筒子紗，將其質量和M11-N與N個筒子紗的質量和MN和當前第N+1個筒子紗的質量相加的總質量M，使M滿足[Yw-ε,Yw+ε]，ε為配重精度，一般固定不變為 60 g，則認為當前第N+1個筒子紗滿足配重要求，可以從2號生產線進入4號生產線執行下一道工序。

3)若M不滿足[Yw-ε,Yw+ε]時，則當前第N+1 個筒子紗不符合要求。用Yw總質量減去前N個筒子紗的質量和MN再除以(12-N)，從立體庫中找出質量在[(Yw-ε-MN)/(12-N),(Yw+ε-MN)/(12-N)]之間的筒子紗，若能找出這樣的筒子紗，則該筒子紗出立體庫，當前第N+1個筒子紗進入立體庫。

4)若找不出符合要求的筒子紗，則當前第N+1個筒子紗從2號生產線末端掉出生產線，不再參與配重。

在筒子紗入庫時，要判斷該筒子紗在輕、正常、重3個區間的哪個區間，再根據立體庫的實際情況從而判斷應進入哪個立體庫。使每個立體庫中的筒子紗盡可能分布均勻，與此同時盡量避免與出庫的立體庫同，保證能持續不斷地進行配重以此提高效率。

4 配重方案處理

在實際配重模式中，每個當前筒子紗經過匹配點時都要進行一次配重方案上的計算，因此就要求控制系統在算法上要提高效率。按照筒子紗最多48個計算，從48個筒子紗中取出n(n≤12的自然數)個，最多的可能有百億多種方案(C(48,12)=6.9×1010)，表1示出從48個筒子紗中取出1到12個筒子紗的最多計算次數。因此，算法開始部分不直接采用排列組合[8-9]的方式進行計算，而是采用人為設定優化后的方案進行計算。

首先，對立體庫中的筒子紗按質量從小到大排列。立體庫中筒子紗最多的時候有48個，冒泡排序的時間復雜度較高，效率慢，因此在排列方式上采用選擇排序，比冒泡排序需要的時間相對較少。選擇排序是每次從待排序的筒子紗質量中選出最小的一個質量，存放在序列的起始位置，然后再從剩余未排序筒子紗質量中繼續尋找最小筒子紗質量，放到已排序序列的末尾，以此類推直至全部待排序的筒子紗質量排完。在立體庫中筒子紗按質量排序完成后，之后的筒子紗進出就可以按照鏈表的的方式插入或刪除，從而進行再一次排序。

表1 實際配重模式下排列組合算法各種 情況的方案次數Tab.1 Number of alternatives in actual counterweight mode under different circumstances

區間分布法如圖4所示，在48個筒子紗按質量從小到大排列好后，再平均分成4個區間，從這4個區間中的每個區間選出n(n≤12的自然數)個，這時的計算量大大減少。從左到右筒子紗的質量從小到大排列。若能找出符合要求的筒子紗，則當前第N+1個筒子紗滿足包裝要求，減少了直接進行排列組合計算的時間。

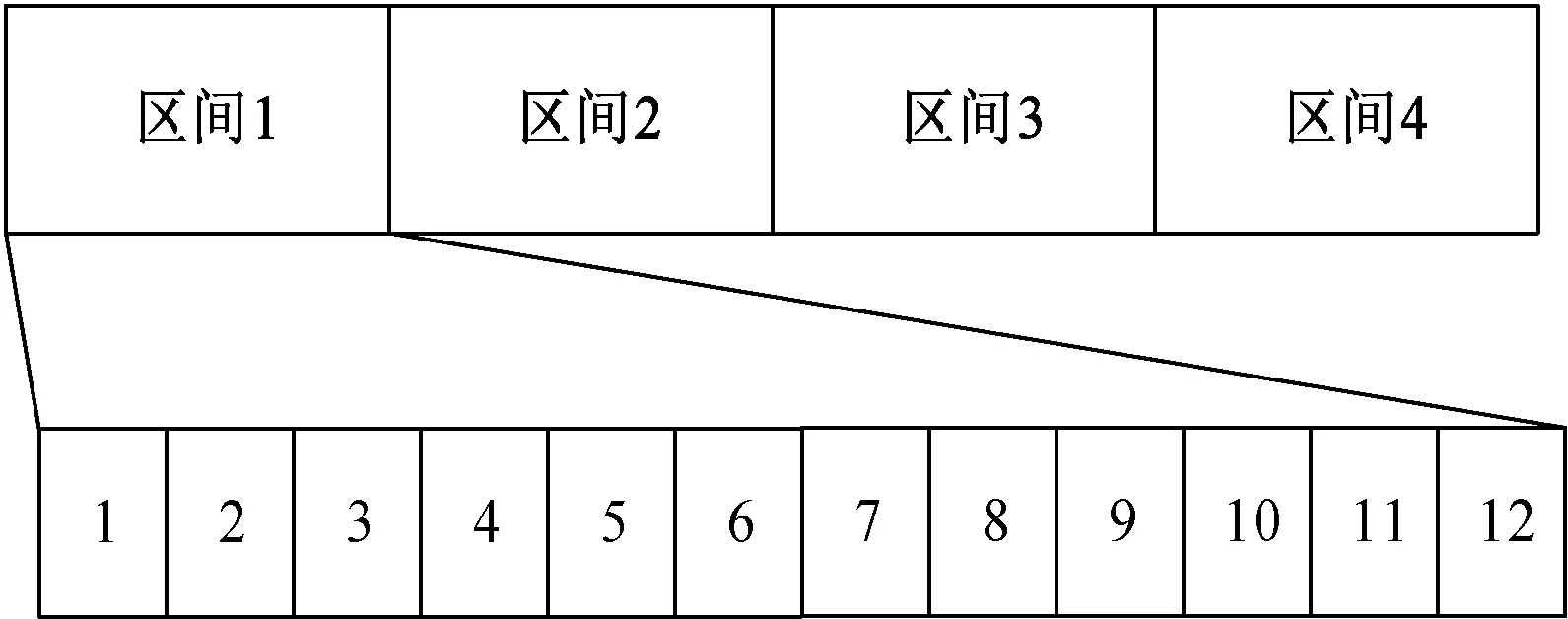
圖4 區間分布圖Fig.4 Interval distribution map

若還是不能找出n個筒子紗，則采用質量配對原則。質量配對法如圖5所示，即保證找出的2個筒子紗其質量相加的平均值與n個筒子紗質量的平均值接近。n為偶數時，需要找到n/2對筒子紗。n為奇數時，先找到(n-1)/2對，再找到一個與平均值接近的筒子紗。然后再進行后續的計算判斷是否滿足。其中質量配對原則要對質量范圍進行對稱劃分成多個區間。根據n個筒子紗的平均質量，向兩邊開始劃分區間。設筒子紗的質量服從均值為n個筒子紗的平均質量Δx，方差為σ2的正太分布。x1，x2是距離Δx相差l的2個點，這2個點的概率密度分別為ρ(x1)，ρ(x2)，|x1-x|=|x2-x|=l，ρ(x1)=ρ(x2)，Δx1=Δx2，如圖5所示。這樣區間就可以分成3部分：輕區間，正常區間，重區間。

圖5 正態分布圖Fig.5 Positive distribution map

正常區間為(a,b)，輕區間為(a-(m+1)r,a-mr)，重區間為(b+nr,b+(n+1)r)，其中a為n個筒子紗質量平均范圍的最小值，b為n個筒子紗質量平均范圍的最大值。r為分區間間隔值，單位是kg。輕區間的分區間與重區間的分區間一一對應，在輕區間的分區間取出筒子紗，則要從與之對應的重區間的分區間再取出一個筒子紗，使2個筒子紗能進行配對。

若以上方法都不能找出n個符合要求的筒子紗，則采用排列組合法計算結果，排列組合法就是從48個筒子紗中取n個，C(48,n)，然后結合遞歸算法得到符合要求的n個筒子紗。用該方法最終判斷能否找出n個筒子紗，即第N+1個筒子紗是否符合要求。若未能找出n個筒子紗，則第N+1個筒子紗不再參與配重，從2號生產線上流出整個系統。

5 仿真與實驗結果

根據以上配重原理及配重方案[10]，編寫仿真程序。用隨機函數rand()產生一個4位數的各個位，其中千位規定為1或者2，得到符合單個筒子紗質量要求筒子紗，輸出參數為筒子紗配重效率，即成功配重的筒子紗個數與總共的筒子紗個數比值的百分數。表2示出采用區間分布法(方法a)，區間分布法及質量配對法(方法b)，區間分布法、質量配對法及排列組合(方法c)對3種配重方法的實驗結果影響。

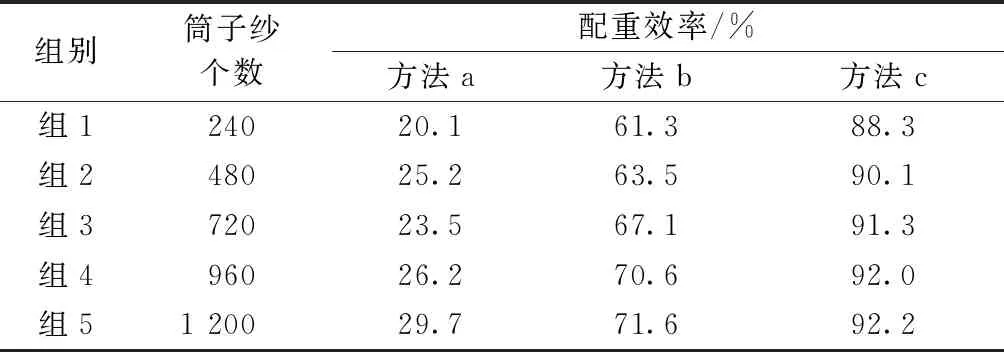
表2 不同配重方法的實驗結果影響表Tab.2 Influence of experimental results of different weighting methods

由表中仿真結果可知，采用區間分布法的效率非常低，大部分筒子紗無法配出。加入質量配對法之后，配重效率有了較大的改善，但還是有一部分筒子紗無法完成配重。最后加入排列組合，計算筒子紗配重的所有可能性。由此可見，采用排列組合能完成所有可以完成的配重，但考慮到時間問題，還是要先采用區間分布及質量配對法，最終效率能達到90%以上，所有配重方法累加的計算時間大約為 4 s，但并不是每個筒子紗都要進行所有配重方法計算。經生產線大量實驗驗證，1包筒子紗(12個)從流水線上開始配重到裝袋，時間不超過70 s，滿足生產線速度的要求，證明本文的配重方案是正確可行的。

6 結束語

根據筒子紗包裝的任務需求，確定了筒子紗配重方案。考慮配重結果以及配重效率等原因，采用區間分布、質量配對和排列組合等方法對筒子紗進行配重處理。通過理論分析和實驗仿真，本文提出的筒子紗配重包裝方案設計合理。設計的系統適用于筒子紗在流水線上打包的應用，能自動、準確、高效地進行配重、打包等工作，操作簡單、靈活，減少了人力，提高了整個生產行業的自動化水平，具有良好的工程應用前景。