一種基于最小二乘法的RTCP自動測量循環(huán)

黃玉彤 方躍熾 劉 沛 李興岳 李耀東 楊立波

(科德數(shù)控股份有限公司，遼寧 大連 116600)

刀具旋轉(zhuǎn)中心編程功能(RTCP)是五軸機(jī)床的重要基礎(chǔ)功能，該功能可以讓用戶通過調(diào)整刀具和工件的相對姿態(tài)來改善切削條件，提高加工效率，是高檔數(shù)控系統(tǒng)的標(biāo)志性功能之一。

由于數(shù)控系統(tǒng)實現(xiàn)RTCP功能時，需要計算旋轉(zhuǎn)軸旋轉(zhuǎn)帶來的線性軸偏差從而進(jìn)行補(bǔ)償，因此機(jī)床的RTCP精度直接受到機(jī)床相關(guān)幾何尺寸測量精度的影響。

一般情況下，機(jī)床在出廠時的RTCP相關(guān)幾何參數(shù)通過手工進(jìn)行標(biāo)定，這就帶來了測量精度準(zhǔn)確性和穩(wěn)定性的波動。同時，機(jī)床需要在一定時間內(nèi)進(jìn)行RTCP參數(shù)的重新校正，這對測量工作耗費的時間提出了一個比較高的要求。目前，國外數(shù)控系統(tǒng)多通過使用測頭的自動測量循環(huán)來實現(xiàn)機(jī)床RTCP相關(guān)參數(shù)的自動標(biāo)定，例如西門子數(shù)控系統(tǒng)使用CYCLE996循環(huán)來進(jìn)行RTCP參數(shù)的自動標(biāo)定。RTCP相關(guān)參數(shù)的自動標(biāo)定功能目前已經(jīng)成為高檔數(shù)控系統(tǒng)不可或缺的重要組成部分。

GNC60系列數(shù)控系統(tǒng)根據(jù)最小二乘法原理開發(fā)相應(yīng)的方法來提高測量循環(huán)的計算精度，有效滿足了自動測量循環(huán)的需求。

1 數(shù)學(xué)原理

1.1 最小二乘法

最小二乘法是一種數(shù)學(xué)優(yōu)化技術(shù)。它通過最小化誤差的平方和尋找數(shù)據(jù)的最佳函數(shù)匹配。利用最小二乘法可以簡便地求得未知數(shù)據(jù)，并使這些求得的數(shù)據(jù)與實際數(shù)據(jù)之間誤差的平方和為最小。

如果數(shù)組X和數(shù)組Y之間存在如下線性關(guān)系[1]

式中：m代表有m個等式，n代表有n個未知數(shù)β，m>n；用向量方式表示為

Xβ=Y

顯然，正常情況下，超越方程無解可言，因此我們將問題轉(zhuǎn)換為使方程的值最小，即實測值與計算值之間誤差最小問題。

1.2 最小二乘擬合圓的實際應(yīng)用

給定兩組數(shù)據(jù)X=[X1,X2,…,Xm],Y=[Y1,Y2,…,Ym],假設(shè)X和Y之間的關(guān)系可以用一個圓的方程表示為如下形式：

R2=(Xi-A)2+(Yi-B)2

令a=-2A,b=-2B,c=A2+B2-R2，則可轉(zhuǎn)化為標(biāo)準(zhǔn)方程形式如下：

(i=1,2,…,m)

的最小值問題。

要求得最小值，只需使方程兩邊同時對系數(shù)a、b、c求偏導(dǎo)，并令所有導(dǎo)數(shù)方程為0，即可求得所需方程的系數(shù)。

同理，我們也可以將此方法擴(kuò)展到空間上實現(xiàn)三組數(shù)據(jù)的所在球體的擬合，進(jìn)而得到球心坐標(biāo)和半徑。

1.3 空間散點擬合平面的計算

給定3組數(shù)據(jù)X=[X1,X2,…,Xm],Y=[Y1,Y2,…,Ym]，Z=[Z1,Z2,…,Zm],可計算出三組數(shù)據(jù)的平均值構(gòu)造的矢量為：

我們定義矩陣D有如下形式：

利用D構(gòu)造三維方陣F：

我們可以求得矩陣F的3個特征值為λ1、λ2、λ3，取最小特征值所對應(yīng)的特征向量為V=[V1,V2,V3]。

假設(shè)X、Y、Z所在的平面的標(biāo)準(zhǔn)方程為

aX+bY+cZ+d=0

根據(jù)上述計算所得參數(shù)，我們可求得

a=V1

b=V2

c=V3

d=-(a×A1+b×A2+c×A3)

此時求得的a、b、c也就是平面的單位法向量。

根據(jù)最小二乘原理，可求得X、Y、Z所在空間球的球心坐標(biāo)A、B、C的值，進(jìn)而計算球心到平面的距離如下：

根據(jù)法向量和球心到平面的距離，我們可求得平面所在圓心的坐標(biāo)為

2 RTCP參數(shù)自動測量循環(huán)

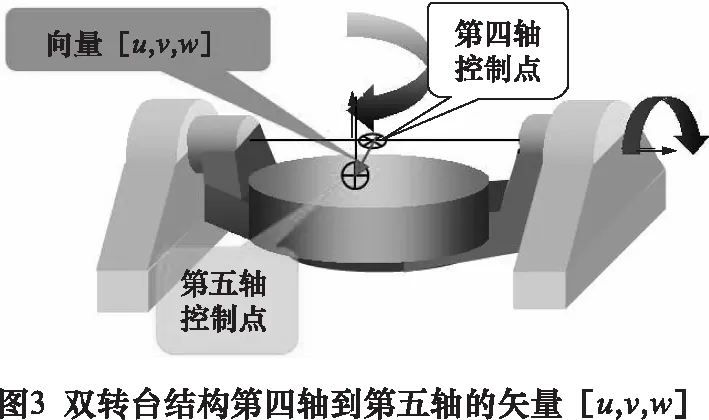
我們以雙轉(zhuǎn)臺XYZAC結(jié)構(gòu)的五軸機(jī)床(圖2)為例，在機(jī)床坐標(biāo)系下測量出AC的軸心坐標(biāo)，可以計算得到機(jī)床坐標(biāo)系下A軸軸心到C軸軸心的矢量和C軸軸心的坐標(biāo)(圖3)，即為需要標(biāo)定的RTCP相關(guān)參數(shù)。

機(jī)床的RTCP參數(shù)自動標(biāo)定方案：

首先放置標(biāo)準(zhǔn)球在轉(zhuǎn)臺上，放置位置為轉(zhuǎn)臺非圓心的任意位置。在保持C軸不動的前提條件下，轉(zhuǎn)動A軸到10個不同位置如圖4所示。數(shù)控系統(tǒng)使用測頭自動測量得到標(biāo)準(zhǔn)球在相應(yīng)A軸位置的10個機(jī)床坐標(biāo)系下的XYZ坐標(biāo)值，如表1所示。數(shù)控系統(tǒng)使用這10個數(shù)據(jù)點進(jìn)行最小二乘法擬合計算得到圓心坐標(biāo)值，作為A軸控制點的坐標(biāo)值。

表1 轉(zhuǎn)動A軸測量的數(shù)據(jù)點

然后，在A=0的狀態(tài)下，轉(zhuǎn)動C軸到10不同的位置，如圖5所示。數(shù)控系統(tǒng)使用測頭自動測量得到標(biāo)準(zhǔn)球在相應(yīng)C軸位置的10個機(jī)床坐標(biāo)系下的XYZ坐標(biāo)值，如表2所示。數(shù)控系統(tǒng)使用這10個數(shù)據(jù)點進(jìn)行最小二乘擬合計算得到圓心坐標(biāo),作為C軸控制點的坐標(biāo)。

表2 轉(zhuǎn)動C軸測量的數(shù)據(jù)點

3 實際機(jī)床的驗證

在科德KMC600S U機(jī)床上使用自帶的無線測頭進(jìn)行了RTCP參數(shù)自動測量循環(huán)的驗證。

根據(jù)上述的RTCP參數(shù)自動標(biāo)定方法，使用表1的數(shù)據(jù)可計算得到在機(jī)床坐標(biāo)系下A軸的控制點坐標(biāo)為[-135.096 8,-0.016 7,95.017 6]。使用表2的數(shù)據(jù)可計算得到在機(jī)床坐標(biāo)系C軸控制點的坐標(biāo)為[-31.430 2,-1.109 9,98.396 6]。兩個點的坐標(biāo)值相減可以得到A軸控制點到C軸控制點的矢量：

[U,V,W]=[-31.4302,-1.1099,98.3966]-

[-135.0968,-0.0167,95.0176]=

[103.6666,-1.0932,3.379]

矢量[U,V,W]和C軸控制點坐標(biāo)[-31.430 2,-1.109 9,98.396 6]即為數(shù)控系統(tǒng)所需的RTCP相關(guān)幾何參數(shù)。

4 結(jié)語

使用最小二乘法對RTCP測量數(shù)據(jù)進(jìn)行擬合，可得到第四軸和第五軸控制點的坐標(biāo)，進(jìn)而求出RTCP所需的標(biāo)定參數(shù)。可以更好更快地達(dá)到保證刀尖點按指令既定軌跡運動的目的。

通過將標(biāo)準(zhǔn)球裝在主軸上，千分表架在機(jī)床臺面上，開啟手動RTCP功能，轉(zhuǎn)動旋轉(zhuǎn)軸，觀察表的跳動量，作為機(jī)床RTCP動作的精度判別標(biāo)準(zhǔn)，如圖7所示。

經(jīng)過數(shù)據(jù)對比和機(jī)床測頭測得的數(shù)據(jù)，測頭補(bǔ)償數(shù)據(jù)(表3和表4)準(zhǔn)確性提高，補(bǔ)償后，打表復(fù)檢RTCP誤差值不斷減小，精度逐步提高。

表3 原始數(shù)據(jù)

表4 補(bǔ)償數(shù)據(jù)

經(jīng)過打表檢查機(jī)床RTCP精度后，再通過加工S形試件，反映機(jī)床的實際RTCP加工精度，如圖8所示。

最終，通過三坐標(biāo)的精度檢測，滿足試件加工的精度要求，報告如圖9所示。

由機(jī)床的RTCP精度檢測和實際S試件加工的精度檢測報告證明該方法得到充分的驗證，并已經(jīng)在GNC60數(shù)控系統(tǒng)上進(jìn)行應(yīng)用。可以保證刀尖點軌跡的正確運動。