基于Hami1ton體系的Lagrange方程盒式傾轉旋翼無人機建模

吳翰，王正平，*，周洲，2，王睿

（1.西北工業(yè)大學 航空學院，西安710072； 2.西北工業(yè)大學 無人機特種技術重點實驗室，西安710065）

隨著“V-247”、“鷹眼”等傾轉旋翼飛行器的產(chǎn)生，飛行器的發(fā)展已由傳統(tǒng)的單一模式逐步向變體以及多功能多用途模式發(fā)展。傾轉旋翼飛行器屬于變體類飛行器的一大重要分支，目前國內外眾多學者已經(jīng)對傾轉旋翼飛行器的布局、氣動［1］及結構［2］進行了深入的研究。針對其動力學模型，國內文獻［3-5］和國外文獻［6］分別基于牛頓-歐拉方程建立了傾轉旋翼飛行器的六自由度模型。由于傾轉旋翼飛行器的結構以及動力學特征均較為復雜，因此基于牛頓-歐拉方程的單剛體動力學建模方法在建立傾轉旋翼飛行器動力學模型時較為復雜。針對以上情況，本文主要提出以下問題：①對于傾轉旋翼飛行器而言，其在傾轉過程中飛行器的質心位置和轉動慣量均將發(fā)生變化，因此如何較為方便地引入動態(tài)傾轉過程中飛行器質心位置與轉動慣量變化對飛行器動力學的影響，值得研究；②對于結構、動力系統(tǒng)較為復雜的飛行器，現(xiàn)有牛頓-歐拉方程基于單剛體思路建立其動力學模型較為復雜，因此能否找尋新的建模方法更為模塊化地建立此類飛行器的動力學模型。

為了解決上述問題，本文依照多體動力學［7-8］思路，將算例盒式傾轉旋翼無人機劃分為由機翼、傾轉旋翼、機體、涵道風扇組成的多剛體系統(tǒng)，其中傾轉旋翼可繞轉動軸發(fā)生轉動。隨后，建立不同剛體部件的力和力矩模型，建立該多剛體系統(tǒng)——盒式傾轉旋翼無人機的非保守力和力矩動能模型、勢能模型、余虛動模型和逆勢能模型；最后采用Hamilton體系下的Lagrange方程［9-10］和第二類Lagrange方程 分別建立該多剛體系統(tǒng)——盒式傾轉旋翼無人機的動態(tài)傾轉過程進行了相應的動力學分析。傾轉旋翼無人機動態(tài)傾轉過程中的質心位置和轉動慣量的變化，實質上都是動態(tài)傾轉過程中傾轉旋翼部分的變化所引起的，因此本文將傾轉旋翼無人機劃分成多剛體系統(tǒng)，通過傾轉旋翼剛體部分質心與機體質心之間的位矢變化來引入動態(tài)傾轉過程中質心位置變化對無人機動力學的影響，通過傾轉旋翼剛體部分轉動慣量的變化來引入動態(tài)傾轉過程中轉動慣量變化對無人機動力學的影響。本文將無人機拆分成多個剛體進行動力學建模，除了可以更為精確地引入無人機的質心位置和轉動慣量變化外，還可以降低無人機建模的復雜度，多個剛體中的每個剛體分別進行建模，再導入Hamilton體系下的Lagrange方程中建立無人機六自由度模型，建模更具有模塊化。

1 運動學模型

1.1 參考坐標系建立

本文所選算例為某盒式傾轉旋翼無人機，其主要由盒式翼布局、涵道風扇以及傾轉旋翼組成。首先基于多體動力學對該盒式傾轉旋翼無人機進行相應假設；其次將該盒式傾轉旋翼無人機劃分為1號機翼、2號機翼、3號機翼、4號機翼、1號涵道風扇、2號涵道風扇、機體、1號傾轉旋翼以及2號傾轉旋翼共計9個剛體；最后以各剛體的質心為坐標原點建立右手坐標系，選取Fe作為地面參考坐標系，具體如圖1所示。需要特別說明的是，本文將左右垂尾與起落架結構共用體和無人機機體共同劃分到無人機的機體模塊中，關于無人機的航向操縱問題，主要采用1號傾轉旋翼、2號傾轉旋翼進行差動控制，因此本文的實質仍然是六自由度模型。

所選算例盒式傾轉旋翼無人機主要具有垂直起降、動態(tài)傾轉以及巡航3個運動過程。垂直起降過程由1號涵道風扇、2號涵道風扇、1號傾轉旋翼和2號傾轉旋翼共同產(chǎn)生向上的拉力；動態(tài)傾轉過程傾轉旋翼部分的傾轉軸帶動1號傾轉旋翼和2號傾轉旋翼發(fā)生傾轉，1號涵道風扇、2號涵道風扇轉速逐漸減為零；巡航過程1號涵道風扇和2號涵道風扇不發(fā)生轉動，僅由1號傾轉旋翼和2號傾轉旋翼提供向前的拉力。該盒式傾轉旋翼無人機的任務剖面如圖2所示，其傾轉旋翼部分傾轉軸與機體內部鉸接如圖3所示。

所選算例盒式傾轉旋翼無人機的具體參數(shù)如表1所示。

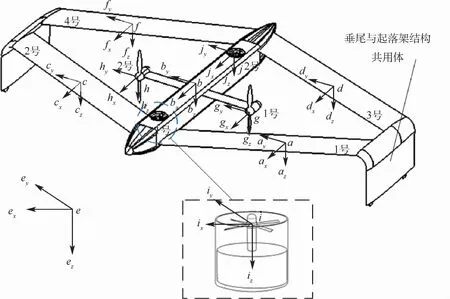
圖1 盒式傾轉旋翼無人機參考坐標系示意圖Fig.1 Schematic diagram of reference coordinate systems for box-wing tilt-rotor UAV

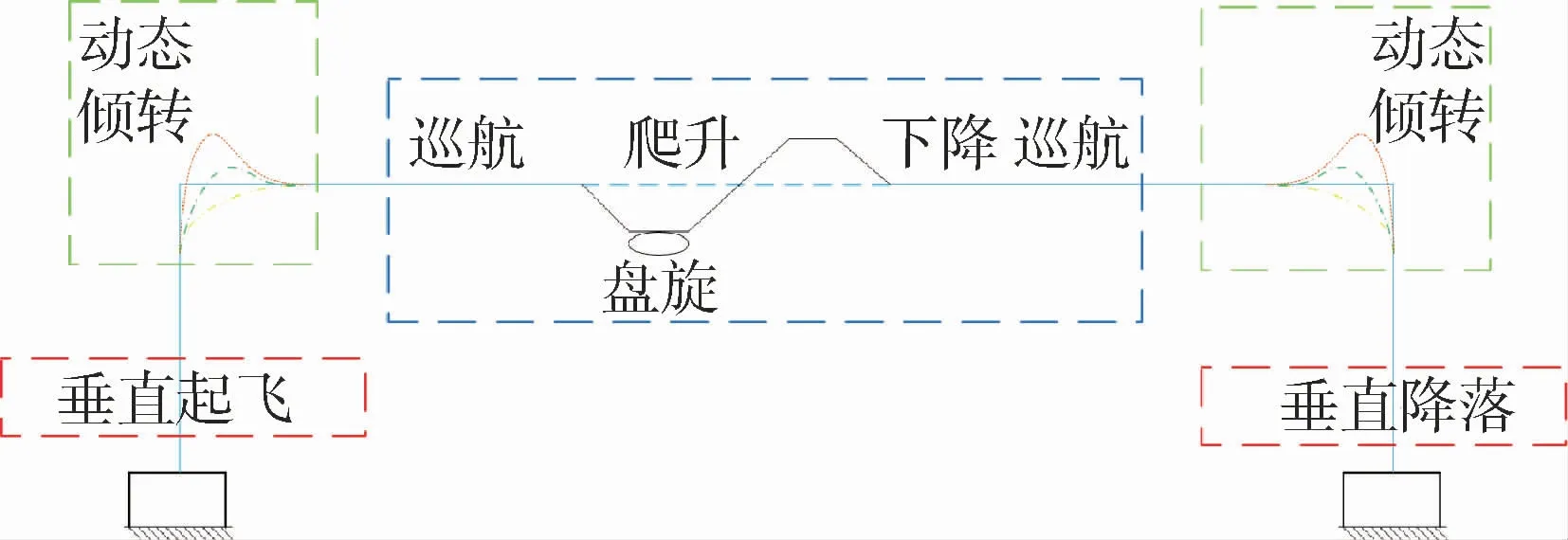
圖2 盒式傾轉旋翼無人機任務剖面Fig.2 Mission profile of box-wing tilt-rotor UAV

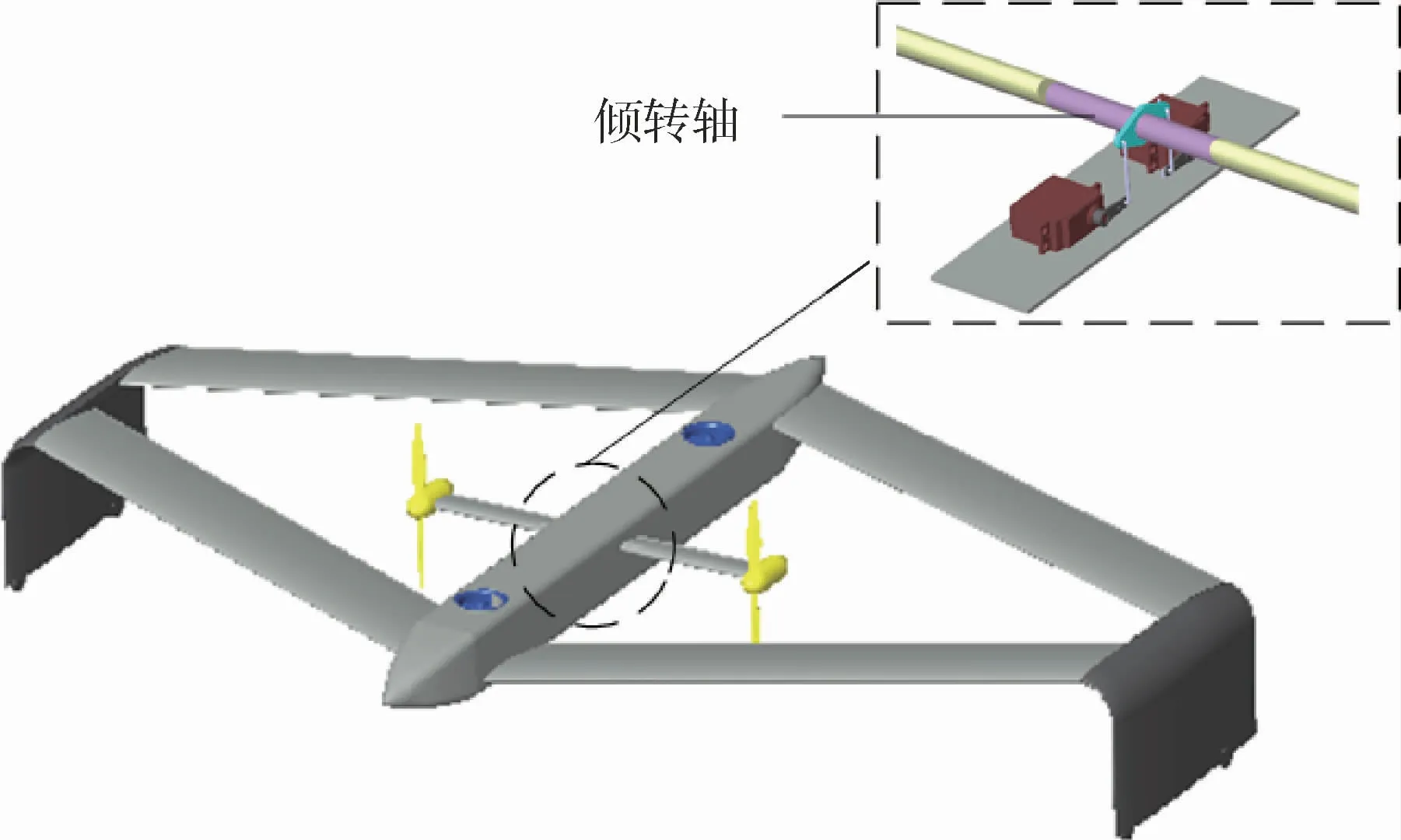
圖3 傾轉軸與無人機機體內部連接示意圖Fig.3 Schematic diagram of internal connection between tilt axis and UAV body

表1 盒式傾轉旋翼無人機具體參數(shù)Tab1e 1 Specific parameters of box-wing ti1t-rotor UAV

1.2 盒式傾轉旋翼無人機廣義坐標選取

本文選取用于描述該盒式傾轉旋翼無人機動力學特征的廣義坐標為

式中：q為盒式傾轉旋翼無人機的廣義坐標矩陣；reb為盒式傾轉旋翼無人機機體質心到參考坐標系原點的位移；qeb為盒式傾轉旋翼無人機機體坐標系相對于參考坐標系的姿態(tài)，在此選用歐拉角進行姿態(tài)參數(shù)化。

2 盒式傾轉旋翼無人機非保守力和力矩模型建立

2.1 機翼氣動力和力矩模型

由于無人機的旋翼一般較小，因此在建立該盒式傾轉旋翼無人機機翼的氣動力和力矩模型時忽略傾轉旋翼尾流對于機翼的影響。由于本文無人機較小，因此在進行機翼的氣動力和力矩建模中，未考慮前后機翼之間的相互氣流干擾影響。以盒式傾轉旋翼無人機的1號機翼為例，由于盒式傾轉旋翼無人機的任務剖面中存在垂直起降、動態(tài)傾轉和前飛巡航3個運動過程，因此其機翼將從90°的大迎角逐步過渡為小迎角，為了建立其動力學模型，可參考文獻［12］選取機翼失速迎角作為分界線，將其動力學模型劃分為大迎角和小迎角兩部分，小迎角部分與正常飛行時一樣，在此不再給出，大迎角部分通過平板擾流系數(shù) 進行建立，具體形式為［14］

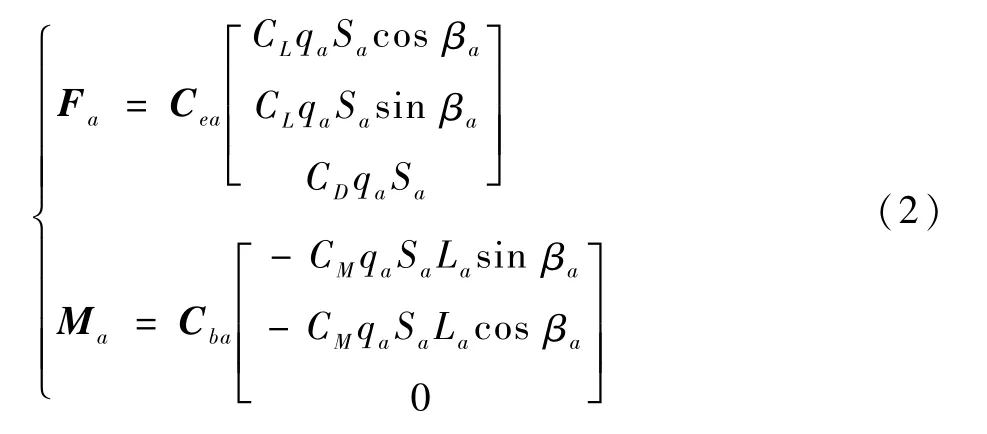
式中：Cea為1號機翼坐標系向參考坐標系的轉換矩陣；Cba為1號機翼坐標系向機體坐標系的轉換矩陣；qa為1號機翼動壓；βa為1號機翼側滑角；La為1號機翼參考長度；Sa為1號機翼參考面積；CL為平板擾流升力系數(shù)；CD為平板擾流阻力系數(shù)；CM為平板擾流力矩系數(shù)。同理可得無人機2號機翼、3號機翼、4號機翼和無人機機體的氣動力和力矩模型為：Fc，F(xiàn)d，F(xiàn)f，F(xiàn)b；Mc，Md，Mf，Mb。需要注意的是，無人機機體的氣動力和力矩模型包含左右垂尾與起落架結構共用體的氣動力和力矩模型。可以通過無人機機體質心與左右垂尾與起落架結構共用體質心之間的位矢，將左右垂尾與起落架結構共用體的氣動力和力矩模型轉換至無人機的機體質心處。

2.2 傾轉旋翼氣動力和力矩模型

傾轉旋翼部分可通過旋翼傾轉軸繞無人機機體坐標系的Y軸發(fā)生偏轉，假設偏轉角為θ，則傾轉旋翼坐標系向無人機機體坐標系的轉換矩陣為

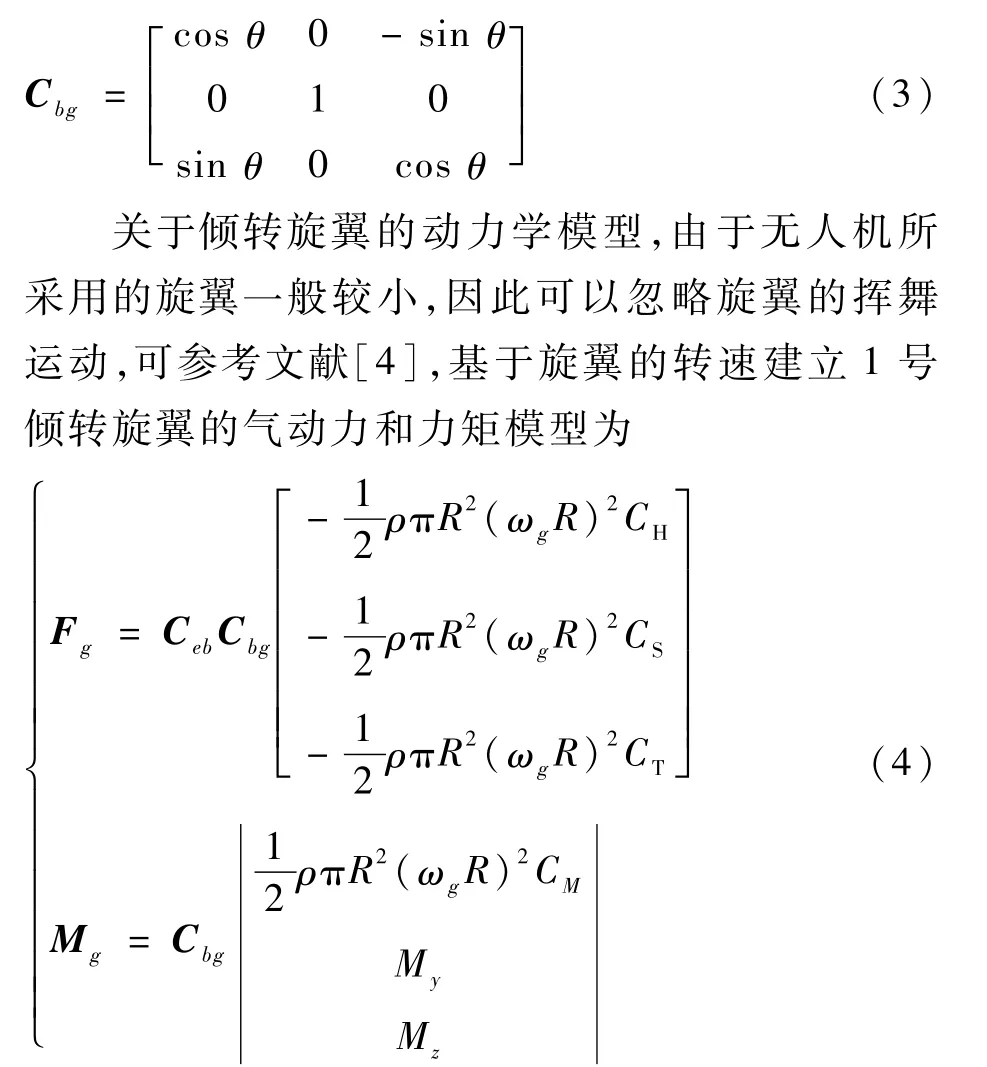
式中：Cbg為1號旋翼坐標系向無人機機體坐標系的轉換矩陣；Ceb為機體全標系向地面坐標系的轉換矩陣；R為1號旋翼的槳葉半徑；ωg為1號旋翼的轉速；CM為1號旋翼的力矩系數(shù)；My、Mz為1號旋翼的力矩分量；CH、CS、CT為1號旋翼的力系數(shù)；ρ為大氣密度。同理可得2號傾轉旋翼的氣動力和力矩模型為：Fh，Mh。

2.3 涵道風扇氣動力和力矩模型

涵道風扇模型與旋翼模型較為相似，可參考文獻［15］，通過增加修正系數(shù)的方式基于旋翼動力學模型，來建立1號涵道風扇的氣動力和力矩模型，其具體結果為

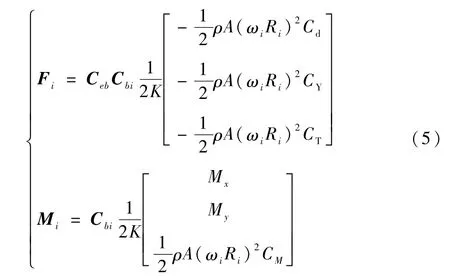
式中：Cbi為1號旋翼坐標系向無人機機體坐標系的轉換矩陣；K為系數(shù)，其與涵道風扇的涵道唇口面積和形狀有關；ωi為1號涵道風扇旋轉角速度；Ri為1號涵道風扇的槳葉長度；A為1號涵道風扇的投影面積；Cd、CY、CT為涵道風扇力系數(shù)；CM為1號涵道風扇的力矩系數(shù)；Mx、My為1號涵道風扇力矩分量。同理可得2號涵道風扇的氣動力和力矩模型為：Fj，Mj。

2.4 盒式傾轉旋翼無人機非保守力和力矩模型

3 Hami1ton體系下Lagrange方程的應用

式中：m為非保守剛體系統(tǒng)的質量；T為剛體系統(tǒng)的動能；J為非保守剛體系統(tǒng)的轉動慣量；U為剛體系統(tǒng)的勢能；Uq為剛體系統(tǒng)的擬勢能；δQH為剛體系統(tǒng)的余虛功；X為剛體系統(tǒng)的質心位移矢量；θ為剛體系統(tǒng)的姿態(tài)。

式中：msum為盒式傾轉旋翼無人機的總質量；Jsum為盒式傾轉旋翼無人機的總轉動慣量矩陣；Jg、Jh、Ji、Jj分別為1號傾轉旋翼、2號傾轉旋翼、1號涵道風扇、2號涵道風扇的慣性矩；Jg、Jh、Ji、Jj分別為1號傾轉旋翼、2號傾轉旋翼、1號涵道風扇、2號涵道風扇的轉動慣量；ωg、ωh、ωi、ωj分別為1號傾轉旋翼、2號傾轉旋翼、1號涵道風扇、2號涵道風扇的轉速。由于動態(tài)傾轉過程中傾轉旋翼部分的轉動慣量矩陣將發(fā)生變化，因此本文通過Jg和Jh在無人機的動態(tài)傾轉過程中隨時間發(fā)生變化，而引入動態(tài)傾轉過程轉動慣量變化對于無人機動力學的影響。

該盒式傾轉旋翼無人機的勢能［18］為

式中：veb為盒式傾轉旋翼無人機機體質心到參考坐標系原點的線速度矩陣；ωeb為盒式傾轉旋翼無人機機體坐標系相對于參考坐標系的角速度矩陣。

再對式（17）運用Green定理可得

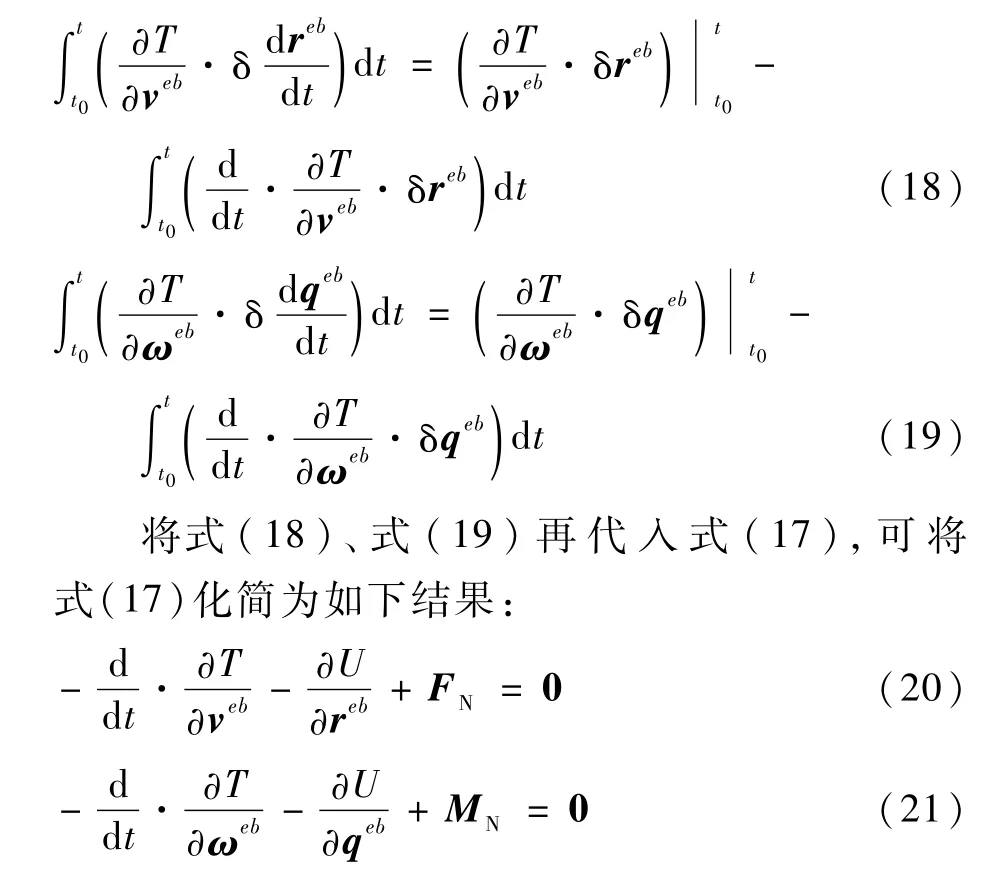
式（20）和式（21）即為盒式傾轉旋翼無人機的動力學模型。其中，式（20）主要描述的是該無人機的質心線加速度與無人機非保守力、保守力之間的關系；式（21）主要描述的是該無人機的角加速度與無人機非保守力矩、保守力矩之間的關系。

4 第二類Lagrange方程的應用

為了與Hamilton體系下的Lagrange方程建模結果進行對比，本文同樣采用第二類Lagrange方程進行該盒式傾轉旋翼無人機的動力學建模，第二類Lagrange方程的具體形式［20］為

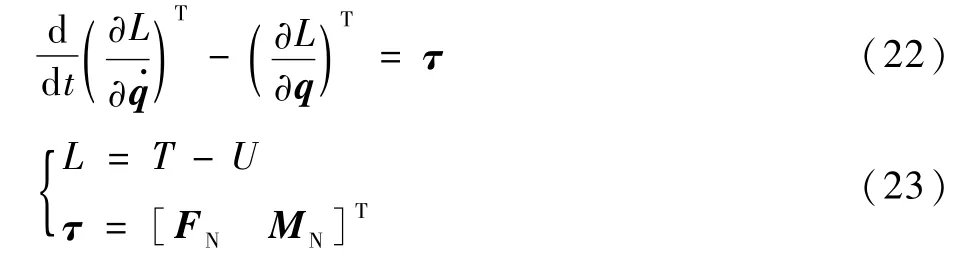
式中：L為拉格朗日函數(shù)；T為無人機動能模型；U為無人機勢能模型。第二類Lagrange方程中字母的含義與上文一致，將式（6）、式（10）、式（13）代入式（22）即可得到基于第二類Lagrange方程所建立的盒式傾轉旋翼無人機的動力學模型。

5 數(shù)值仿真

5.1 實驗驗證

首先為了驗證本文建模方法的合理性，采用Hamilton體系下Lagrange方程建模方法、第二類Lagrange方程建模方法和傳統(tǒng)牛頓-歐拉方程單剛體方法對盒式傾轉旋翼無人機進行動力學建模，并與該盒式傾轉旋翼無人機的飛行實驗數(shù)據(jù)進行對比，實驗無人機的構型具體如圖4所示。

圖4 實驗盒式傾轉旋翼無人機示意圖Fig.4 Schematic diagram of experimental box-wing tilt-rotor UAV

該盒式傾轉旋翼無人機主要進行了滑跑起飛、巡航飛行以及滑跑著陸的實驗過程，本文選取無人機爬升到巡航階段的實驗數(shù)據(jù)與數(shù)值仿真結果進行對比，其中所選取對比的無人機初始時刻實驗數(shù)據(jù)為：無人機初始高度1 m，前飛速度10 m／s，上升速度0.3 m／s，俯仰角5°，其余參數(shù)均為零。在實驗過程中，無人機左右螺旋槳轉速位于2000～2500 r／min之間。基于Hamilton體系下Lagrange方程、第二類Lagrange方程以及牛頓-歐拉單剛體方法所建動力學模型的數(shù)值仿真初始條件均為：reb＝［0 0－1］Tm，qeb＝［0 5 0］T（°），veb＝［10 0－0.3］Tm／s，ωeb＝［0 0 0］Trad／s。具體對比結果如圖5～圖7所示。需要特別說明的是，3次仿真實驗和實物實驗采用的均為PID控制方法進行控制，其目標軌跡為飛行高度60 m，前飛速度20 m／s，俯仰角不進行控制。

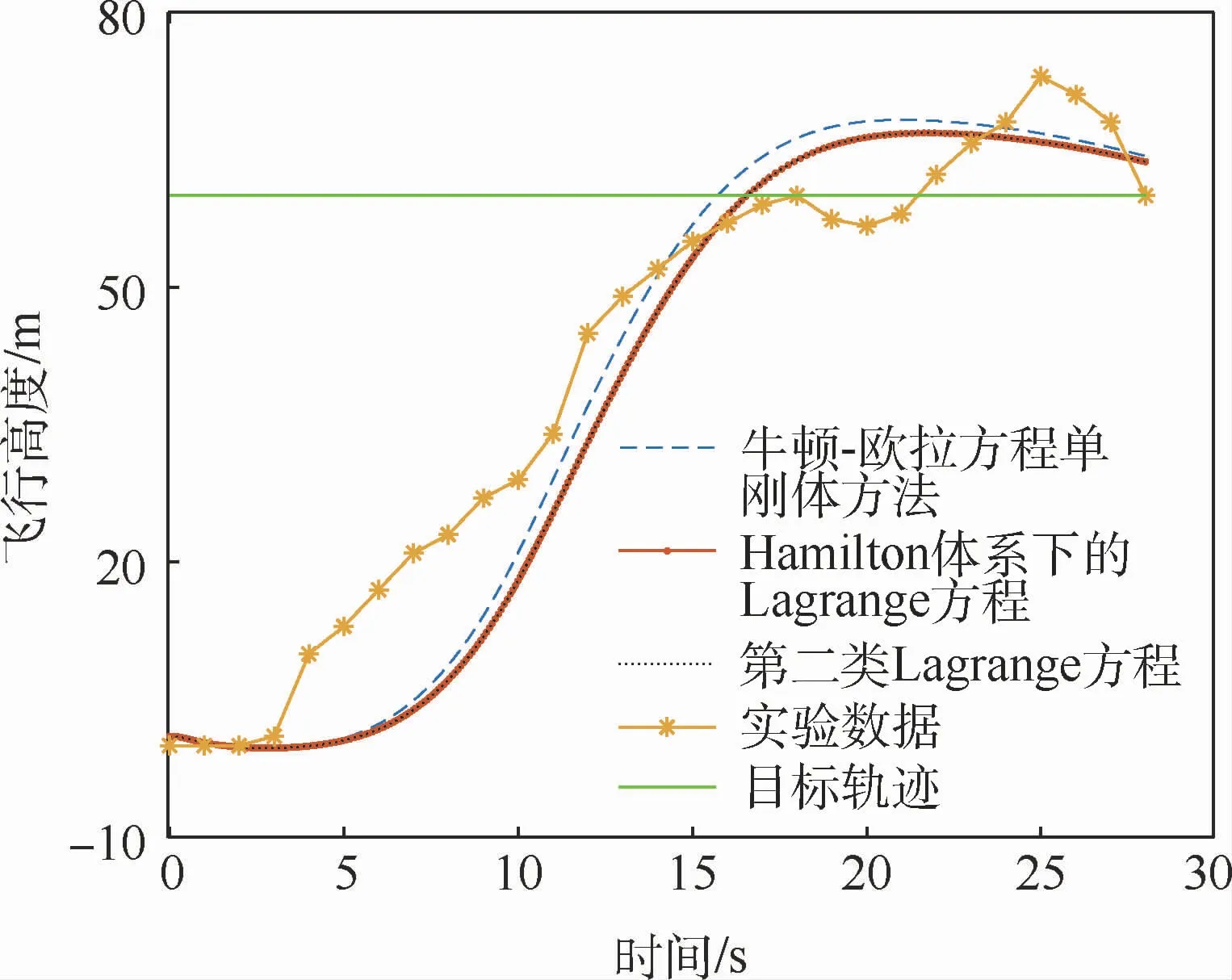
圖5 無人機飛行高度仿真與實驗結果對比Fig.5 Comparison of UAV flight height between simulation and experimental results

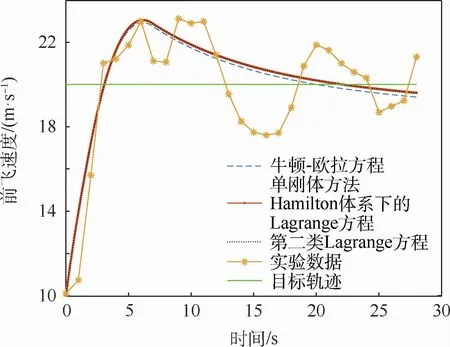
圖6 無人機前飛速度仿真與實驗結果對比Fig.6 Comparison of UAV forward velocity between simulation and experimental results

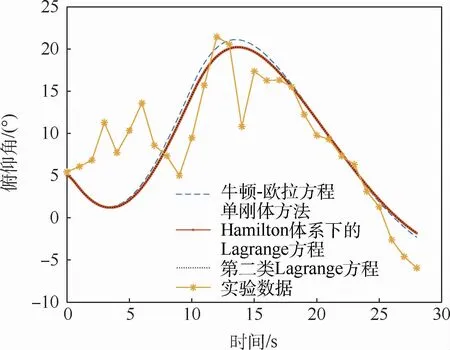
圖7 無人機俯仰角仿真與實驗結果對比Fig.7 Comparison of UAV pitch angle between simulation and experimental results

通過圖5～圖7數(shù)值仿真結果與飛行實驗數(shù)據(jù)的對比可以得出以下結論：首先，圖5～圖7中Hamilton體系下Lagrange方程、第二類Lagrange方程、牛頓-歐拉方程以及實驗數(shù)據(jù)的趨勢基本一致，這些均驗證了本文動力學建模方法可適用于該無人機的動力學建模，且所建模型是合理的。其次，通過圖5～圖7中Hamilton體系下Lagrange方程和第二類Lagrange方程仿真結果的一致性，可以驗證在相同的非保守力和力矩模型下，這2類建模方程的結果是一樣的，但是牛頓-歐拉方程單剛體仿真結果與Hamilton體系下Lagrange方程和第二類Lagrange方程仿真結果存在差異，其主要原因為：單剛體和多剛體建模方法無人機的轉動慣量和質心位置存在不同。除此之外，圖6中實驗數(shù)據(jù)與仿真結果略有差異，其主要原因在于：在飛行實驗過程中，盒式傾轉旋翼無人機左右螺旋槳的轉速保持在2 000 r／min～2 500 r／min之間，而不是完全固定在某一數(shù)值，因此其會導致盒式傾轉旋翼無人機前飛速度實驗數(shù)據(jù)與仿真結果的差異。

5.2 動態(tài)傾轉階段數(shù)值仿真

5.1節(jié)已驗證本文模型的合理性，本節(jié)將本文所建模型應用于盒式傾轉旋翼無人機，對其最為關注的動態(tài)傾轉階段進行動力學仿真研究。由于5.1節(jié)已驗證Hamilton體系下Lagrange方程和第二類Lagrange方程在非保守力和力矩模型相同的情況下，建模結果一致，因此在本節(jié)仿真曲線中將不再引入第二類Lagrange方程的仿真結果。需要說明的是，本文所選樣機目前僅進行了滑跑起飛以及巡航試驗，還未實現(xiàn)垂直起飛及傾轉過渡功能。因此，在本節(jié)動態(tài)傾轉過程研究中，并未進行試驗數(shù)據(jù)與仿真數(shù)據(jù)的對比。

傾轉旋翼無人機動態(tài)傾轉過程時間的長短會影響其動態(tài)傾轉階段的動力學特征，為了進行對比找尋最為合適的動態(tài)傾轉方式，分別選取傾轉過程總時間為5 s、10 s、15 s進行對比，整個仿真過程1 號傾轉旋翼、2 號傾轉旋翼轉速保持2 000 r／min不變，初始時刻其余狀態(tài)量均為零。整體仿真過程為盒式傾轉旋翼無人機由靜止開始垂直上升到動態(tài)傾轉再到巡航，盒式傾轉旋翼無人機垂起過程為0～15 s，期間旋翼傾轉軸與無人機機體的夾角為0°；動態(tài)傾轉階段從15 s開始，期間旋翼傾轉軸與無人機機體的夾角由0°線性變?yōu)椋?0°，1號涵道風扇、2號涵道風扇的轉速線性減少至零；前飛巡航階段旋翼傾轉軸與無人機機體的夾角為－90°，1號涵道風扇、2號涵道風扇無轉速。具體仿真結果如圖8～圖12所示。

圖8 盒式傾轉旋翼無人機前飛速度Fig.8 Forward velocity of box-wing tilt-rotor UAV

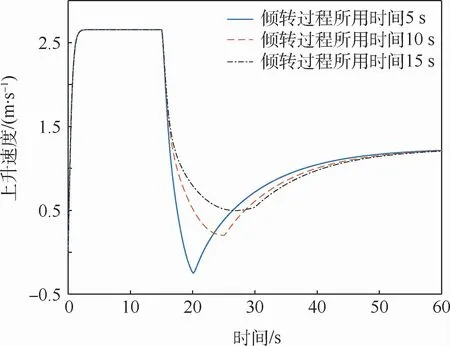
圖9 盒式傾轉旋翼無人機上升速度Fig.9 Rising velocity of box-wing tilt-rotor UAV

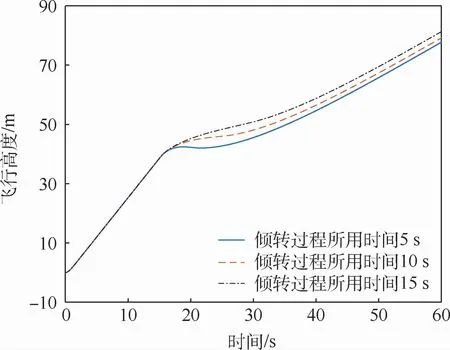
圖10 盒式傾轉旋翼無人機飛行高度Fig.10 Flight height of box-wing tilt-rotor UAV

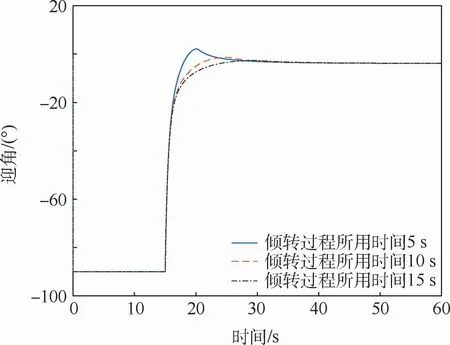
圖11 盒式傾轉旋翼無人機迎角Fig.11 Angle of attack of box-wing tilt-rotor UAV

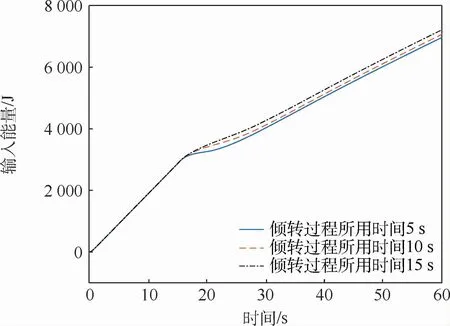
圖12 盒式傾轉旋翼無人機輸入能量Fig.12 Input energy of box-wing tilt-rotor UAV

通過圖8～圖12仿真結果的對比可以得到，傾轉過程所用時間越短，無人機上升速度在動態(tài)傾轉過程中的突變越大，無人機動態(tài)傾轉軌跡越不光滑，無人機傾轉過程中的掉高越明顯，但無人機所需要的輸入能量較少；無人機的傾轉時間越長，無人機上升速度在動態(tài)傾轉過程中的突變越小，無人機動態(tài)傾轉軌跡越光滑，無人機傾轉過程中的掉高越少，但無人機所需要的輸入能量越多。因此，具體采用何種動態(tài)傾轉方式，還需要基于本模型的仿真結果，根據(jù)無人機的實際應用情況來進行確定。接下來對仿真曲線圖8、圖11和圖12進行解釋。由于1號涵道風扇、2號涵道風扇轉速減為零這個過程所用時間是和動態(tài)傾轉過程所用時間一致的，因此傾轉時間越長，1號涵道風扇、2號涵道風扇對無人機所做功越多，該盒式傾轉旋翼無人機的輸入能量越多，這與仿真結果完全一致；由于本文選取無人機的迎角作為參考迎角，因此對于無人機垂起過程而言無人機的迎角為－90°，隨后進行動態(tài)傾轉，最后回歸到正常巡航迎角，整體與無人機迎角仿真曲線一致；對于前飛速度而言，無人機在傾轉過后前飛速度最終趨于一致，這是由于巡航時僅由傾轉旋翼提供拉力，而旋翼轉速一致，因此巡航時拉力一致，無人機前飛速度最終結果一致。

6 結 論

通過某盒式傾轉旋翼無人機的建模與仿真，可以得到如下結論：

1）本文基于Hamilton體系下的Lagrange方程和第二類Lagrange方程推導并建立了盒式傾轉旋翼無人機的動力學模型，并通過與實驗結果的對比驗證了建模方法的合理性，通過仿真結果可以看出，在相同非保守力和力矩模型的情況下，基于Hamilton體系下的Lagrange方程和第二類Lagrange方程建立的動力學模型的實質是一致的，Hamilton體系下的Lagrange方程能夠適用于傾轉旋翼飛行器的動力學建模。本文建模的缺點在于：未引入無人機前后機翼之間的干擾和傾轉旋翼尾流對無人機后機翼的影響，后續(xù)可從這兩方面進行改進。

2）Hamilton體系下的Lagrange方程主要是將建模系統(tǒng)離散成多體系統(tǒng)，再分別考慮每個系統(tǒng)的質心位置以及轉動慣量變化，最終通過不同剛體間的位移約束引入不同系統(tǒng)質心位置的變化，通過疊加的方式引入不同系統(tǒng)轉動慣量的變化，這也是該方法在建立變體類飛行器動力學模型時的優(yōu)點。除此之外，該方法將無人機劃分成多剛體系統(tǒng)，分別建立每個剛體的模型，再導入Hamilton體系下的Lagrange方程建立無人機六自由度模型，其更具模塊化，可降低建模的復雜度。

本文研究了傾轉過程時間長短對于傾轉旋翼無人機動力學的影響，除此之外動態(tài)傾轉過程中傾轉旋翼轉速變化、涵道風扇轉速變化等均將對傾轉無人機的動力學產(chǎn)生影響，因此應當綜合考慮這些因素進而制定最為合適和安全的動態(tài)傾轉過渡方式。