虛假數據注入攻擊下的自適應補償控制

李小杭， 張志虎， 宋春林， 吳強， 董方勇

(北方信息控制研究院集團有限公司 信息總體部， 江蘇 南京 211100)

0 引言

隨著物聯網、傳感器網絡、嵌入式系統和計算智能等技術的發展，信息世界和物理世界的交互、協同和融合在不斷加強，信息物理系統(CPS)作為一種新型智能系統應運而生。

CPS是指把分布于不同位置的控制器、執行器、傳感器和被控對象通過網絡連接起來，形成一種閉環的分布式反饋控制系統，其結構圖如圖1所示。近年來，CPS的研究被持續關注，取得了一系列很有意義的研究成果，已經逐漸成為國際控制領域的一個研究熱點[1]。

圖1 CPS 基本結構Fig.1 Basic structure of cyber-physical system

隨著CPS的迅速發展，由此而產生的安全問題對社會所產生的危害也越來越大。例如，德國政府于2011年11月公布了《高技術戰略2020》，其中一項重要戰略就是工業4.0，其核心之一是通過CPS創新制造方式，實現“智能工廠”。我國在黨的十八大報告中突出強調CPS的重要性，指明“推動信息化和工業化深度融合，加快傳統產業轉型升級”的發展方向。此外，2012年，破壞力十分巨大的“火焰”病毒在中東地區廣泛傳播，對石油工業等重要控制系統的正常運行造成了極其嚴重的沖擊[2]。虛假數據注入攻擊是一種特殊類型的攻擊，最初應用于智能電網[3]。

虛假數據注入攻擊是一種意圖破壞系統穩定性且保持針對檢測機制隱身性的攻擊。針對智能電網中的虛假數據注入攻擊，文獻[4-6]做了一系列研究。Mo等通過系統模型的特征值，設計了一種針對控制系統中傳感器的虛假數據注入攻擊，破壞系統穩定性且避開了卡方檢測器的檢測[7]。文獻[8]研究了幾類傳感器與執行器虛假數據注入攻擊的情況，并設計了在執行器和傳感器同時進行攻擊情況下完全消除對檢測器攝動的方法。在此基礎上，文獻[9-10]通過可達性理論，以攻擊者角度分析了在虛假數據注入攻擊下的系統狀態可達域。這種攻擊對模型知識精確程度的要求程度高，但可造成系統不穩定。

容錯控制研究在系統執行器和傳感器發生故障時仍能保證系統穩定性并盡可能保證系統性能。文獻[11]針對執行器失效故障，研究了重構控制器的自適應容錯控制策略。文獻[12]研究了在執行器存在失效、卡死和中斷故障情況的直接自適應容錯控制問題。Hao等又針對帶有量化現象和執行器故障的網絡控制系統，利用積分滑模方法設計了容錯控制器[13]。這類容錯控制方案對于受到數據攻擊的CPS控制問題具有深遠影響。例如，文獻[14]應用線性矩陣不等式(LMI)技術設計了拒絕服務(DoS)攻擊下的補償機制。文獻[15-16]應用自適應方法補償了系統中存在的數據攻擊。文獻[17]考慮了動態解決虛假數據注入攻擊的解決問題。文獻[18]針對履帶式裝甲車在受到干擾下的自適應控制問題進行了研究。

針對CPS中的虛假數據注入攻擊問題，國內外學者展開了相關研究工作，然而尚未見到考慮系統具有自適應補償控制器時虛假數據注入攻擊對系統性能指標影響的報道。本文在系統具有自適應補償控制器的情況下，攻擊者向系統發起常值虛假數據注入攻擊以及有界時變虛假數據注入攻擊信號時，開展了系統的動態情況分析。主要研究工作包括以下兩個方面：

1) 研究系統具有自適應補償器且虛假數據注入攻擊的攻擊信號為常值信號時，自適應補償控制方法對系統性能指標的影響。

2) 研究系統具有自適應補償控制器且虛假數據注入攻擊的攻擊信號為有界時變值信號時，自適應補償控制方法對系統性能指標的影響。

本文的主要創新點為：針對CPS中的虛假數據注入攻擊，提出一種新型自適應補償控制器，以保證攻擊者成功注入虛假數據后系統仍然能夠穩定運行并保持良好的動態性能。

1 問題描述

線性連續時不變系統遭受虛假數據注入攻擊時，網絡攻擊的系統結構如圖2所示。圖2中包括系統控制器和執行器，由控制器對執行器發出控制指令u(t)，由控制器到執行器的過程使用無線網絡進行數據發送。在CPS中，攻擊者可以攻擊無線網絡來攔截和修改控制器發送的數據，從而對系統進行破壞，攻擊信號為a(t)。

圖2 虛假數據注入攻擊下的系統結構Fig.2 Structure of system under false data injection attack

1.1 系統模型

(1)

y(t)=Cx(t)+υ(t)，

(2)

式中：x(t)∈Rn為狀態空間向量，n為維度；u(t)∈Rn為控制輸入向量；y(t)∈Rm為傳感器的測量向量，m為維度；υ(t)∈Rm為傳感器有界外部測量噪聲;初始狀態x0=0；A為適當維度的系統矩陣；B為適當維度的輸入矩陣；C為適當維度的輸出矩陣。針對此類控制系統的特點，本文引入現代控制理論中的下列假設來進行分析：

假設1：(A,B)是完全可控的。

假設2：(A,C)是完全可觀測的。

假設3：系統正常運行或受到有界虛假數據注入攻擊。

1.2 針對執行器的虛假數據注入攻擊模型

為了規劃自適應補償控制問題，需要建立針對執行器的虛假數據注入攻擊模型：

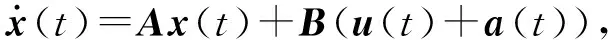
(3)

y(t)=Cx(t)+υ(t)，

(4)

1.3 研究問題

針對線性時不變連續系統中執行器受到虛假數據注入攻擊的情況，本文研究如何運用自適應控制方法的補償器，保證攻擊者成功注入虛假數據后系統仍然能夠穩定運行，動態特性良好的問題。

2 自適應補償控制器設計

本文研究在系統受到常值和有界時變虛假數據注入攻擊情況下系統帶有自適應補償控制器的系統動態性能。首先定義攻擊策略，然后設計針對不同虛假數據注入攻擊的自適應補償控制器。

2.1 常值攻擊情況下的自適應補償控制

類似于現有文獻[6]中的攻擊模型，本文假設攻擊者能夠攔截和修改傳輸與執行器相關的數據[6]，定義控制輸入為

u(t)=Kx(t)-(t)，

(5)

式中：K為反饋控制增益矩陣。自適應控制律為

(6)

式中：P為n×n維正定矩陣。

定理1考慮執行器受攻擊系統(3)式，在控制器(5)式和自適應律(6)式的作用下，能夠保證最終閉環系統的所有信號是有界的并且狀態能漸近收斂到0.

證明鑒于(A,B)完全能控，存在正定矩陣P∈Rn×n，使得P(A+BK)+(A+BK)TP<0成立。為方便表示，不妨令P(A+BK)+(A+BK)TP=-Q，其中Q為正定矩陣，則

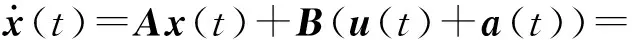
(7)

(8)

由此可以看出本文設計

(9)

的自適應律即可實現控制目標。證畢。

2.2 有界時變攻擊情況下的自適應補償控制

本節考慮有界時變攻擊情況下針對執行器攻擊的自適應補償控制方法。首先，將有界時變攻擊信號設置上界，即轉化為與2.1節常值情況下虛假數據注入攻擊類似的情況進行分析。最后，證明在受攻擊的系統滿足定理2條件下可以使系統狀態收斂到0，實現受攻擊以后系統動態性能良好的目標。

考慮帶有有界擾動情況下的下列系統：

(10)

y(t)=Cx(t)+υ(t)，

(11)

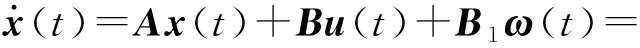
(12)

考慮在攻擊‖a(t)‖≤b，b為未知正常數值情況下的系統，‖a(t)‖為a(t)的范數，可以得到

(13)

由于‖a(t)‖≤b，Fω(t)有界，不妨令a(t)+Fω(t)≤k，其中k為需要估計的未知參數。因此，定義控制輸入信號

u(t)=Kx(t)+u1(t)，

(14)

式中：u1(t)為自適應補償控制器控制輸入，

(15)

(16)

定理2考慮執行器受攻擊系統(13)式，在控制器(14)式、(15)式和自適應律(16)式的作用下，能夠保證最終閉環系統的所有信號是有界的，并且狀態能漸近收斂到0.

證明鑒于(A,B)完全能控，存在正定矩陣P∈Rn×n，使得P(A+BK)+(A+BK)TP<0成立。為方便表示，不妨令P(A+BK)+(A+BK)TP=-Q. 構造李雅普諾夫方程：

(17)

對其求導，可以得到

(18)

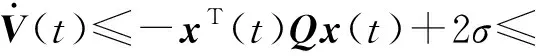
(19)

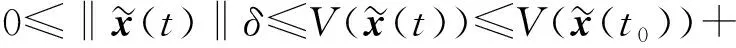
(20)

(21)

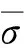
3 仿真實例

為了論證針對虛假數據注入攻擊的自適應補償控制方法的有效性，在此引用文獻[18]中的參數作為仿真實例。本文考慮一個2階系統，其中動態模型如下：

(22)

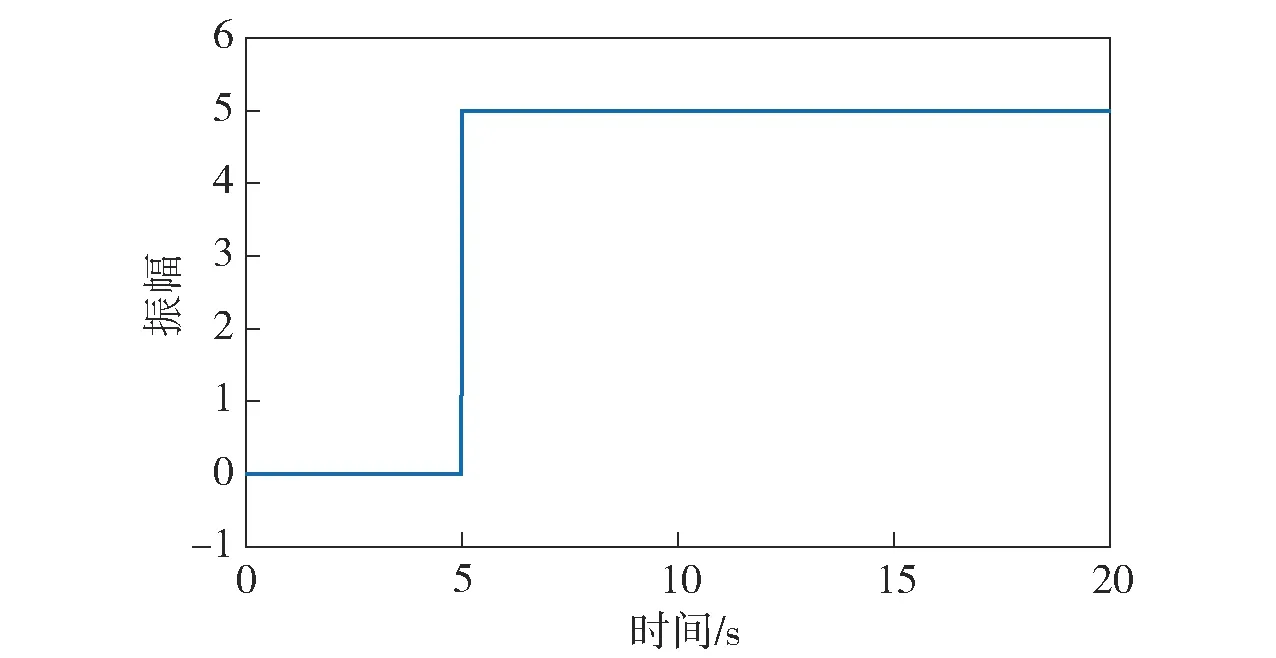
圖3 常值攻擊信號Fig.3 Constant attack signal

圖4 常值攻擊信號估計值Fig.4 Estimation of constant attack signal

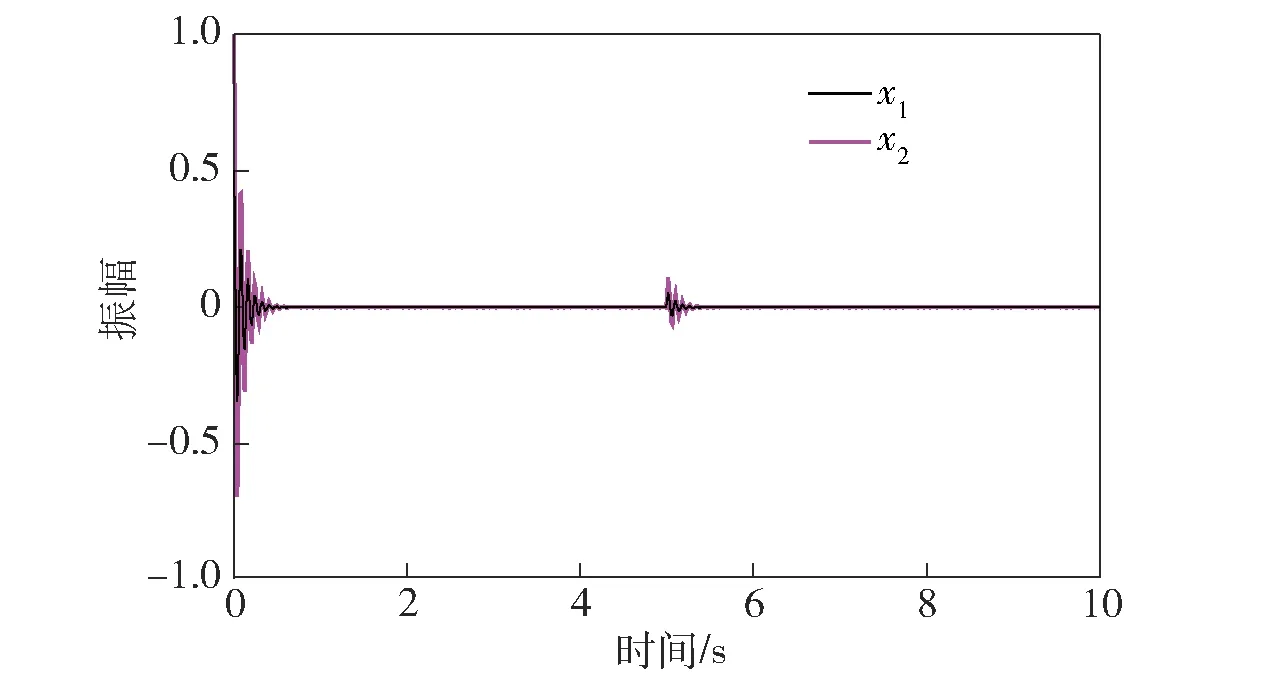
圖5 自適應控制下的系統狀態響應曲線Fig.5 Response curves of system state under the adaptive control

當系統執行器受到有界時變虛假數據注入攻擊‖a(t)‖=3×exp(-t/5)時，仿真結果如圖6～圖8所示。其中：圖6是系統運行5 s后有界時變虛假數據注入攻擊信號圖像；圖7顯示了應用自適應補償控制器后系統對攻擊信號的估計值，從中可以看出系統在13 s以后(即攻擊運行8 s后)系統估計的攻擊信號值始終比實際值大，這與本文提出的理論方法一致；圖8顯示了應用自適應補償控制器后系統狀態的動態變化，從中看出系統在運行13 s以后(即攻擊運行8 s后)系統的狀態漸進收斂為0，自適應補償控制效果良好。

圖6 有界時變攻擊信號Fig.6 Attack signal with bounded boundry

圖7 有界時變攻擊信號估計Fig.7 Estimation of bounded time-varied attack signal

圖8 自適應控制下的系統狀態響應曲線Fig.8 Response curves of system state under the adaptive control

4 結論

本文主要研究了系統執行器在受到常值虛假數據注入攻擊與有界時變虛假數據注入攻擊時的自適應補償控制器設計方法。根據自適應機構提供的在線估計信息，構造自適應補償控制器，用于抵消虛假數據注入攻擊產生的偏差，并采用Barlalat引理對該自適應律的收斂性給予了嚴格的數學證明。該自適應補償控制算法應用到虛假數據注入攻擊中，結果表明：所設計的自適應律具有收斂速度快、估計參數準確等優點；該補償控制算法能夠基本上補償虛假數據注入攻擊產生的影響，證明最終的閉環系統所有信號是有界的，并且系統狀態能夠漸近收斂到0.