基于交叉效率排序多目標進化算法的備件供應優化

王亞東， 石全， 尤志鋒， 王芳， 夏偉，2

(1.陸軍工程大學石家莊校區 裝備指揮與管理系, 河北 石家莊 050003；2.陸軍步兵學院石家莊校區 機械化步兵系, 河北 石家莊 050083)

0 引言

充足及時的備件供應是維修工作順利開展的前提，也是裝備保障工作的重中之重。備件供應優化和方案決策需要綜合考慮時間、風險、成本等多方面因素，優化目標多元，建模和求解難度較大[1]。因此備件供應網絡優化和供應方案決策始終是備件保障的重點和難點問題。

目前很多學者對備件供應優化開展了相關研究。魏國強等對需求點的優先級聚類排序，研究了資源不足情況下的備件調度模型，以供應開始時間最早和調運線路最少為目標建立模型，并通過賦權將多目標轉化為單目標優化進行求解[2]。劉喜春等建立了典型3級備件供應保障結構下的戰時多階段備件供應保障規劃模型，以期望缺件量為目標建立無約束單目標優化模型，通過迭代方法獲得備件供應保障優化策略[3]。張斯嘉等建立了基于可信性理論的戰時多目標保障物資供應優化模型，采用蝙蝠算法求解多目標優化問題[4]。秦進等以最小化系統成本為目標，考慮應急資源數量、備用容量和位置數量等約束，建立了考慮服務可靠性的應急資源布局優化模型，提出一種基于矩陣實數編碼的遺傳算法求解方法[5]。Fazli-Khalaf等以最小化設施之間的總供應成本和運輸時間，同時最大化供應可靠性為目標，建立了應急供應三目標優化模型[6]。Zhang等以最大限度地減少運輸時間、運輸成本和不滿足度為目標，建立了多目標三階段隨機規劃模型，采用基于隸屬度模糊輔助變量的替代單目標模型來處理多目標模型[7]。Mohammadi等以最大化總預期需求覆蓋、最小化總預期成本并最小化節點之間滿意率為目標，建立了一個多目標隨機規劃模型，并采用多目標粒子群優化算法來解決這個模型[8]。Su等以完全響應時間和緊急資源成本為目標構建雙目標乘法約束整數線性規劃模型，并使用差分進化算法搜索模型的最優解[9]。綜上所述可以看出，目前相關研究大多采用多目標優化模型。這是因為單目標優化的優化目標單一，考慮因素較少，不適于備件供應優化決策。但是，多目標優化求解難度大且得到的是一系列非支配解集，無法確定唯一的最優方案，因此不利于進一步決策。

本文為解決備件供應優化決策問題，以供應時間、風險、成本為目標，構建備件供應多目標優化模型。在求解算法上，本文受到了帶精英策略的非支配排序遺傳算法(NSGA-II)的啟發，在多目標進化算法(MOEA)的基礎上，采用交叉效率數據包絡分析(DEA)對存檔中的非支配解進行排序。一方面，可以指導種群向最優效率個體進化；另一方面，可以計算得到非支配解的自評效率和互評效率值，從而對眾多非支配解進行排序、決策出最優解。

1 備件供應多目標優化模型

1.1 問題描述

某備件供應網絡由后方倉庫、野戰倉庫和用裝單位3級節點組成。用裝單位的維修力量對損壞裝備進行維修時產生備件需求。后方倉庫為備件的供應點，考慮到安全問題，通常距離任務前線相對較遠。因此在后方倉庫和用裝單位之間設置野戰倉庫，野戰倉庫通常靠前設置，接收后方倉庫供應的備件并前送至用裝單位。備件供應優化則是根據備件需求、節點以及供應網路的狀態信息確定最佳的備件供應方案，從而保證以較短的時間、較低的總風險和較少的成本滿足備件需求。

本文備件供應模型建立在以下假設之上：1)以某類關鍵備件為研究對象。2)節點之間的備件運輸成本和運輸時間已知且為定值，節點之間運力充足。3)野戰倉庫的開放費用、庫存費用、最大儲備量均為已知且為定值。4)備件未能滿足用裝單位需求而造成的后果用缺件損失表示，缺件損失越大的用裝單位表明其優先級越高；用裝單位的備件需求量和缺件損失已知。5)備件全部到達野戰倉庫后再統一向用裝單位進行分配和供應。6)供應網路的中斷風險僅發生在野戰倉庫和用裝單位之間。7)暫不考慮越級供應以及同級之間橫向供應的情況。

1.2 變量及其說明

i：后方倉庫的序號，i=1，2，…，I，I為后方倉庫的數量；

j：野戰倉庫的序號，j=1，2，…，J，J為野戰倉庫的數量；

k：野戰倉庫的序號，k=1，2，…，K，K為用裝單位的數量；

Uj：第j個野戰倉庫最大容量；

dk：第k個用裝單位的備件需求量；

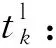
Rij：備件從后方倉庫i運至野戰倉庫j的中斷風險，假設中斷發生在途中；

Rjk：備件從野戰倉庫j運至用裝單位k的中斷風險，假設中斷發生在途中；

xij：后方倉庫i向野戰倉庫j供應備件的數量；

xjk：野戰倉庫j向用裝單位k供應備件的數量；

yj：二進制變量，用來標注野戰倉庫j的開放情況，yj=1表示開放，yj=0表示關閉。

1.3 模型建立

目標函數1：備件供應的總時間最短。

(1)

目標函數2：備件供應的總風險最低。

(2)

目標函數3：備件供應總成本最小。

minC=Co+Ct+Ci+Cs,

(3)

式中：Co表示野戰倉庫的開放成本；Ct表示運輸成本；Ci表示備件在野戰倉庫的庫存成本；Cs表示缺件損失。各項成本計算如下：

(4)

(5)

(6)

(7)

滿足以下約束：

(8)

(9)

(10)

(11)

(12)

xij∈N+,xjk∈N+,yj={0,1}.

(13)

式中：N+為正整數。約束(8)式、(9)式表示未開放的野戰倉庫不參與備件供應，同時還規定了供入的備件數量不能超過野戰倉庫的最大容量；約束(10)式規定了用裝單位的備件需求應得到滿足；約束(11)式規定了野戰倉庫備件的供出量應不超過供入量；約束(12)式規定了對于每個用裝單位，備件供應的延遲時間應不超過允許的最大截止時間。這里規定的延遲時間與目標函數中的總供應時間有所區別。供應總時間用來體現調運車輛數量和總里程等信息，而延遲時間則表示備件從供應開始到全部到達所消耗的時間；約束(13)式規定了決策變量的類型和取值范圍。

2 二次目標交叉效率排序多目標進化算法

為了求解備件供應多目標優化模型的最優解以及得到最終方案，本文提出了一種二次目標交叉排序多目標進化算法(SGCES-MOEA)。該算法采用進化計算的基本框架，在每次迭代中將種群中的非支配解放入存檔，并從存檔中選擇精英個體指導種群的進化。與傳統進化計算不同的是，SGCES-MOEA采用了類似于NSGA-Ⅱ的排序機制來選擇精英個體。NSGA-Ⅱ先根據種群中個體被支配的次數對個體分層，再對同一層的個體計算擁擠度距離，并根據擁擠度距離對每一層個體進行排序。第一層為非支配解(被支配次數為0)，該層擁擠度距離最大的個體為精英個體[10]。

SGCES-MOEA從NSGA-Ⅱ得到啟發，用非支配個體的效率值代替擁擠度距離進行排序，從而選擇出精英個體。相對于擁擠度距離，效率可以反映出個體在優化模型中的綜合指標，具有實際意義。個體的效率值計算則采用改進的DEA法。每個非支配個體相當于一個決策單元(DMU)，根據優化模型計算得到各指標值后，再利用DEA評估模型計算個體的效率值。SGCES-MOEA的基本步驟如圖1所示。

圖1 SGCES-MOEA的基本流程Fig.1 Basic flow chart of SGCES-MOEA

2.1 進化策略

進化策略是對父代種群個體進行的變異、交叉、選擇等操作，從而產生子代種群的過程。通過進化，種群不斷得到改善，從而獲得較優解。

步驟1變異。令ps=ps1,ps2,…,…,psh,…,psD為第s個父代個體向量，psD為第s個個體向量ps上的第D個變量；vs=vs1,vs2,…,…,vsh,…,vsD為根據變異策略產生的變異個體向量，vsD為第s個變異個體向量vs上的第D個變量。本文采用DE/current-to-best/1策略進行變異：

vs=ps+F×(pe-ps)+F×(pr-ps)，

(14)

式中：pe為當前種群中的最優個體；pr為從存檔中隨機選取的個體，且ps≠pe≠pr；F為變異率。

(15)

式中：rsh為[0,1]之間均勻分布的隨機數；CR為交叉率，CR∈[0,1]，即當變異個體vs上第h個變量vsh對應的隨機數小于交叉率時，交叉個體向量us上對應變量ush取父代個體ps對應變量xsh，否則保留變異個體上的變量值。

步驟3選擇。根據種群中的父代個體和交叉個體的適應度函數，一一比較其支配關系。若某父代個體被對應的交叉個體支配，則用該交叉個體替換對應父代個體。最終得到的個體構成選擇個體種群，作為子代個體進入下一次迭代。

步驟4更新存檔。將子代種群中的非支配解放入存檔中，與存檔個體混合后，再次比較支配關系，選出混合種群的非支配解作為新的存檔。

2.2 適應度函數及編碼

由于本文構建的多目標優化模型屬于帶約束的優化問題，本文采用動態罰函數法處理模型約束[11]：

(16)

式中：x為決策變量向量；f(x)為適應度函數；O(x)為目標函數；M0為初始懲罰因子；ni為當前算法迭代次數，maxni為算法最大迭代次數；MK為懲罰系數；P(x)為約束違反度，

(17)

m為約束條件的總個數，ch(x)為約束違反度。若不等式約束表示為lh(x)≤0的形式，其約束違反度ch(x)=max(0,lh(x))；若等式約束表示為hh(x)=0的形式，其約束違反度ch(x)=max (0,|hh(x)-ε|)，ε為一個很小的實數。

如圖1所示，取直徑為170 mm，直徑偏差范圍為0～0.8 mm的帶輪進行實驗。對帶輪邊緣輪廓進行測量，通過雙目視覺圓弧輪廓特征提取和匹配之后，得出邊緣外輪廓點的空間三維坐標。圖2所示為求得的帶輪邊緣外輪廓點云圖及空間圓弧擬合圖，共獲得266個邊緣外輪廓點的三維坐標。利用本文擬合優化方法，對上述點云進行8次擬合，平均迭代數為6 895次。擬合結果如表1所示。

2.3 指標計算

根據DEA模型指標的性質，將評價指標分為輸入型指標和輸出型指標，輸入型指標的值越小、對應DMU的效率越高，輸出型指標的值越大、DMU的效率越高。

本文的輸入型指標包括：

1)供應成本：計算公式即目標函數(3)式；

2)供應時間：計算公式即目標函數(1)式；

3)約束違反度：由于模型還涉及容量以及流量平衡等約束，將優化結果的約束違反度作為指標之一。模型的總體約束違反度計算公式為(17)式。

輸出型指標包括：

圖2 個體編碼方式示意Fig.2 Chromosome individual coding pattern

1)可靠性指標：用備件供應的風險衡量，其值為總風險的倒數。風險計算公式為目標函數(2)式；

2)時效性指標：用延遲時間即供應開始到最后一波備件到達的時間衡量，取延遲時間的倒數。延遲時間的計算公式為約束(12)式；

3)滿足度：用各用裝單位的備件滿足度表示，計算公式即約束(10)式。

2.4 二次目標交叉效率排序

算法采用DEA模型計算個體效率。傳統DEA由Cooper等提出，其構建的固定規模收益的CCR模型[12]如下：

(18)

(19)

μra≥ε,υba≥ε,r=1,2,…,so,b=1,2,…,mi.

(20)

式中：Edd表示DMUd的自評效率，DMUd為第d個DMU；r為輸出指標序號；so為輸出指標的總個數；Yrd表示DMUd的第r個輸出指標；mi為輸入指標的總個數；μrd為Yrd的權重；Xbd表示DMUd的第b個輸入指標；υbd為Xbd的權重；Ea為第a個決策單元DMUa的自評效率；Yra表示第a個決策單元DMUa的第r個輸出指標；μra為Yra的權重；n為決策單元的個數；Xba為第a個DMUb的第b個輸入指標;νba為Xba的權重；ε為比任何正數都小的非阿基米德數。約束(19)式規定了所有DMU的效率值應介于0～1之間。約束(20)式規定了所有權重應大于0.

傳統DEA模型還存在兩個缺點：1)由于其采用的是自評效率，只能區別有效單元(效率值等于1)和無效單元(效率值小于1)，無法對有效單元進行排序；2)計算得到的輸入和輸出權重不唯一[13]。針對第1個問題，SGCES-MOEA通過計算各DMU的交叉效率，可以對所有DMU進行評估和排序。針對第2個問題，SGCES-MOEA通過構建二次目標模型，使得權重向量取值唯一。

交叉效率計算方法如下。

(21)

根據CCR模型對每個DMU分別求其自評效率，再根據(21)式求每個DMU的相互之間的互評效率，得到互評效率矩陣：

則DMUa的交叉效率為

(22)

由于CCR中求得的最優權重組合可能不唯一，在利用(21)式計算交叉效率時其值也不唯一。為解決此類問題，Doyle等提出了通過引入二次目標的方法，在多重最優解中選擇一組最優解，以最終確定每個DMU的交叉效率[14]。常用的二次目標方法有激進型策略和慈善型策略[15]。本文的二次目標交叉效率DEA模型如下：

(23)

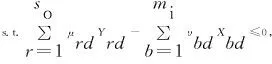
(24)

(25)

(26)

(27)

(28)

(29)

(30)

μra≥ε，r=1,2,…,so；

(31)

υba≥ε，b=1,2,…,mi.

(32)

3 算例及其分析

3.1 算例描述

以某次演習任務的維修備件的支援保障為例，共有6個用裝單位在前線執行演習任務。根據裝備的損壞情況，通過維修任務確定需要的備件種類和數量。為檢驗支援保障能力，部分關重件未隨部隊攜行，僅由后方供應。維修備件的儲備由兩個后方倉庫承擔，同時在后方倉庫和用裝單位之間有4個備選可開設野戰倉庫。備件由后方倉庫運送至野戰倉庫，再根據前線需求由野戰倉庫進行分配轉運至各個用裝單位。后方倉庫、野戰倉庫以及用裝單位的相關數據見表1～表5.

表1 單位備件在各節點間的運輸時間Tab.1 Transportation times of spare parts between nodes h

表2 單位備件在各節點間的運輸成本Tab.2 Transportation costs of spare parts between nodes 元

表3 野戰倉庫和用裝單位間路線中斷風險Tab.3 Disruption risk of transit routes from fieldwarehouses to demand units

3.2 多目標優化結果

利用SGCES-MOEA對算例模型進行求解，本文采用MATLAB 2014b軟件進行編程，平臺為個人筆記本(Intel Core i5-6300HQ (2.3 GHz/L3) CPU和4.00 GB RAM)。相關參數設置如下：種群規模為100，外部存檔規模為100，最大迭代次數為500，變異因子為0.9，交叉率為0.8，選擇閾值為0.8，初始懲罰因子為10 000 000，懲罰系數為10 000.

表4 野戰倉庫的庫存容量、單位備件庫存成本、開設費用Tab.4 Inventory capacity, unit spare parts inventorycost, and running cost of field warehouse

通過計算，算法共求得13個非支配解，每個解代表一個供應方案。表6給出了所有方案的輸入指標、輸出指標以及交叉效率和自評效率的值。其中滿足度1～6為6個用裝單位的備件滿足度。由表6可以看出，13個方案中有10個方案為有效方案，其自評效率均為1，僅通過自評效率無法進一步從這10個方案中選出最優方案。通過計算和比較各方案的交叉效率，可以選出最優方案，其交叉效率值最大為0.927 8.

表5 用裝單位的備件需求、缺件損失、最大延遲時間Tab.5 Spare parts requirements, missing loss, maximumdelay time of demand units

表6 SGCES-MOEA求解結果Tab.6 Solved results of SGCES-MOEA

3.3 靈敏度分析

通過算例的計算結果可以看出，通過SGCES-MOEA可以求得模型的非支配解并根據效率進行排序，從而選出最優解。為了進一步驗證本文的排序策略對算法和結果的影響。分別用未進行排序的MOEA和采用自評效率排序的多目標進化算法(SES-MOEA)對模型進行優化，將其結果與SGCES-MOEA的結果進行比較。

表7為MOEA求得的16個非支配解的相關指標，由于未采用排序機制而沒有計算自評效率和交叉效率值。16個DMU僅存在非支配關系，無法進一步決策出最優的供應方案。表8為SES-MOEA求得的7個非支配解的相關指標及其自評效率值。由表8可以看出SES-MOEA結果中有4個DMU的效率值等于1，為有效DMU，剩余3個為非有效DMU. 此時僅通過自評效率同樣無法進一步選擇最優供應方案。

表7 MOEA求解結果Tab.7 Solved results of MOEA

表8 SES-MOEA求解結果Tab.8 Solved results of SES-MOEA

為了驗證3種算法求得方案的優劣，將SGCES-MOEA、MOEA和SES-MOEA求得的所有DMU混合后作為整體，進一步使用本文的二次目標交叉效率DEA法計算所有DMU的自評效率和交叉效率，并根據交叉效率進行排序。所有DMU的效率值如圖3所示。從圖3中可以看出，SGCES-MOEA對應的交叉效率值普遍較大，而MOEA對應的交叉效率值普遍較小，SES-MOEA介于二者之間。通過計算發現：SGCES-MOEA對應DMU的平均交叉效率值為0.878 5；MOEA對應DMU的平均交叉效率值為0.723 8；SES-MOEA對應DMU的平均交叉效率值為0.752 7. 由此可見，SGCES-MOEA的效果要優于其他兩種算法。

圖3 3種算法結果的效率值對比Fig.3 Comparison of efficiency values of solved results of three algorithms

4 結論

本文主要解決備件供應優化決策問題，同時考慮時間、風險和成本3個目標，建立了備件供應網絡優化的多目標優化模型。使用基于交叉效率排序的MOEA求得模型的非支配解集，并決策出最優供應方案。研究內容的主要貢獻有：1)提出的多目標優化算法和約束處理方法可以解決備件供應的多目標約束優化問題；2)提出的基于效率排序策略可以進一步對非支配解排序，同時可以指導算法向效率最大的個體收斂；3)通過計算交叉效率克服了僅憑自評效率無法對有效單元進行排序的問題；4)提出的二次目標DEA模型解決了評估權重不唯一的問題。綜上，本文的模型和算法為解決備件供應優化以及最優備件供應方案決策提供了框架和求解思路。