基于Henstock積分在區(qū)間子列上的可和性研究*
李 偉
(集美大學(xué)理學(xué)院, 福建 廈門 361021)
20世紀(jì)初,在測(cè)度理論[1]基礎(chǔ)上建立的Lebesgue積分[2](簡(jiǎn)稱L-積分),是經(jīng)典積分理論的突破,它為現(xiàn)代實(shí)函數(shù)論的研究奠定了基礎(chǔ)[3].但是,由于L-積分是絕對(duì)型的,即“f∈L?|f|>∈L”,使得L-可積范圍受到了限制,例如,廣義黎曼可積不一定是L-可積,由此可見,L-積分還存在一定的局限性.1912年,Denjoy從函數(shù)的可微性和ACG*性質(zhì)出發(fā),定義了Denjoy積分[4](簡(jiǎn)稱D-積分),1914年,Perron定義了Perron積分[4](簡(jiǎn)稱P-積分).1921年,人們證明了D-積分與P-積分其實(shí)是等價(jià)的,并證明了它們是Riemann積分[5](簡(jiǎn)稱R-積分)的全部推廣,且各自均包容了L-積分.這種積分的本質(zhì)是非絕對(duì)型的,因此,也稱之為非絕對(duì)型積分[6].但由于D-積分和P-積分的定義非常繁雜,這樣就給積分理論的推廣及應(yīng)用帶來(lái)了諸多困難.1957年、1958年,J.kurzweil和R.Henstock分別獨(dú)立地給出了一種完全Riemann型的積分,稱之為kurzweil-Henstock積分[7,8],簡(jiǎn)稱Henstock積分(簡(jiǎn)記為H-積分).20世紀(jì)80年代初,人們證明了“H=D=P”.由于Henstock積分無(wú)需用到繁雜的測(cè)度理論,加之又是Riemann型的,因此,它的出現(xiàn)讓積分理論充滿了生機(jī),使得對(duì)有關(guān)理論的研究和應(yīng)用煥然一新[9,10].
本文就非絕對(duì)型Henstock積分理論進(jìn)行研究.首先闡述δ(x)精細(xì)分法及Henstock積分概念,然后引進(jìn)區(qū)間[a,b]上的非絕對(duì)型Henstock積分的有限可和性等性質(zhì)定理,進(jìn)而在Henstock引理等有關(guān)理論基礎(chǔ)上,給出Henstock積分在區(qū)間子列上的可和性的定理(定理6),并給予詳細(xì)證明.
1 定義及其預(yù)備知識(shí)
定義1[7]區(qū)間[a,b]上給出正值函數(shù)δ(x)>0,所謂在區(qū)間[a,b]上的分法T是δ(x)精細(xì)的,是指T的有序分點(diǎn):a=x0 ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi)), (i=1,2,…,n). 可以看出所謂[a,b]上的δ(x)精細(xì)分法T,是區(qū)間[xi-1,xi]與ξi所組成的集偶: {([xi-1,xi],ξi),i=1,2,…,n}, 它滿足: 2)[xi-1,xi]兩兩無(wú)公共內(nèi)點(diǎn); 3)ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi)). 因此,以后提到區(qū)間[a,b]上的δ(x)精細(xì)分法T,有時(shí)可直接寫為: {([xi-1,xi],ξi),i=1,2,…,n}, 為避免產(chǎn)生誤解,簡(jiǎn)寫為: {([u,v],ξ)} 或 {[u,v],ξ}. 定義2[7]設(shè)函數(shù)f(x)定義于區(qū)間[a,b],若存在常數(shù)I,滿足下列關(guān)系:對(duì)任給的ε>0,存在δ(x)>0,對(duì)任何δ(x)精細(xì)分法T,其分點(diǎn)為:a=x0 (*) 則稱f(x)在[a,b]上是Henstock意義下可積,簡(jiǎn)稱H-可積的,且I稱為f(x)在[a,b]上的H-積分,記為: 以上Henstock積分稱為廣義Riemann積分;也稱為完全Riemann積分. 這個(gè)積分定義不同于Riemann積分定義,主要在于它的積分和并不要求對(duì)所有充分細(xì)密分法及一切ξi∈[xi-1,xi]都能使(*)式滿足,而僅僅是要求對(duì)于任何δ(x)精細(xì)分法中相應(yīng)的分點(diǎn)xi與結(jié)點(diǎn)ξi使(*)式滿足就夠了.這樣減弱了對(duì)分法及ξ選擇的要求,就有可能使本來(lái)不是Riemann可積的函數(shù),成為Henstock可積的函數(shù). 定理1[8]若函數(shù)f1(x)、f2(x)在[a,b]上Henstock可積,k為實(shí)數(shù),則f1(x)+f2(x)和kf1(x)在[a,b]上也是Henstock可積的,且: 定理2設(shè)u 證明:令f=fX[u,w]+fX[w,v],其中X[u,w]和X[w,v]分別為[u,w]上和[w,v]上的特征函數(shù),則定理的結(jié)論由定理1即可得證. 定理3[8](H-積分的有限可和性)設(shè){[ai,bi]}為[a,b]中互不相重的有限區(qū)間列,且[a,b]= 定理4[8](Henstock引理) 設(shè)g(x)是區(qū)間[a,b]上的Henstock可積函數(shù),且存在原函數(shù)G(x),即 則對(duì)任給ε>0,存在δ(x)>0,使得對(duì)[a,b]上的任何δ(x)精細(xì)子分法,即 a≤a1 且:ξi∈[ai,bi]?(ξi-δ(ξi),ξi+δ(ξi)).(注意,所謂精細(xì)子分法是不要求[a,b]=∪[ai,bi]的精細(xì)分法.)有: 定理5[11]設(shè)F(x)在[a,b]上連續(xù),且F(x)是f(x)在每個(gè)[c,d]?[a,b]上的Henstock原函數(shù),則F(x)也是f(x)在[a,b]上的Henstock原函數(shù). 定理6 設(shè)E是一個(gè)有界閉集,a,b分別是其下、上確界,{Ik}是[a,b]內(nèi)連接于E的區(qū)間列.如果f(x)在E和每個(gè)Ik上H-可積,且 則f(x)在I=[a,b]上H-可積,且 其中O(H,f,Ik)為f(x)的原函數(shù)Fk在Ik上的振幅,簡(jiǎn)記為Ok. 證明:當(dāng)Ik為有限時(shí),由Henstock引理立即得證.下面假設(shè)Ik(k=1,2,…)為無(wú)限序列. 任給ε>0,由定理5,因f(x)在Ik=[ak,bk]上H-可積,故在Ik上存在δk(ξ)>0,存在Ik上定義的實(shí)函數(shù)Fk,對(duì)所有的Ik上的δk精細(xì)分法D,有 |∑kf(ξ)(v-u)-Fk(IK)|> < 2-Kε. (1) 因Fk在Ik上的振幅Ok=O(H,f,Ik)組成的級(jí)數(shù)收斂,故存在N,使得 (2) |∑*f(ξ)(v-u)-A (3) 注意,這里ξ∈E.還要求當(dāng)ξ≠a、b、ak、bk(k=1,2,…,N)時(shí),滿足 在[a,b]上定義δ(ξ)為 任作δ-精細(xì)分法D,注意到 (ⅰ)對(duì)于k≤N,ak,bk必屬于分點(diǎn)集{ξ},對(duì)于端點(diǎn)ak,當(dāng)其不是分法區(qū)間端點(diǎn)時(shí),即: ak∈(u,v)?[ak-δ(ak),ak+δ(ak)],將[u,v]分為[u,ak]與[ak,v]; 對(duì)于bk也作類似的分解,分解后仍是δ-精細(xì)分法,且∑f(ξ)(v-u)的值不變.由此必有子族 {[u,v];[u,v]?(ξ-δ(ξ),ξ+δ(ξ),ξ∈[ak,bk]}覆蓋[ak,bk],k=1,2,…,N; (ⅱ)分解后的δ-精細(xì)分法還必有子族 {[u,v];[u,v]?(ξ-δ(ξ),ξ+δ(ξ),ξ∈E}覆蓋E; (ⅲ)對(duì)于k>N,可能沒有分法D中的ξ∈(ak,bk),但如果有若干ξ∈(ak,bk),則它們必相鄰. 由于|∑kf(ξ)(v-u)-Fk(ak,bk)|>表示ξ∈[ak,bk] (k≤N)的部分和,由(1)知小于2-kε,因此 (4) |∑*f(ξ)(v-u)-A|>表示ξ∈E中的部分和,由(3)知小于ε; ∑k*[f(ξ)(v-u)-Fk(u,v)]表示[ak,bk]上δk精細(xì)分法中的部分和(如果沒有則為0),由Henstock引理,|∑k*[f(ξ)(v-u)-Fk(u,v)|><2·2-kε,因此 (5) 于是: ε+ε+2ε+2ε=6ε. 證畢. 該定理說(shuō)明:前述的有限可和性定理成為該定理的推論.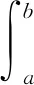
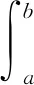
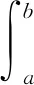
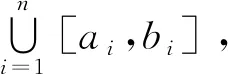
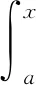
2 定理及其證明
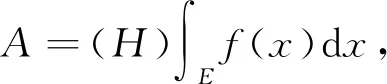
|> <ε.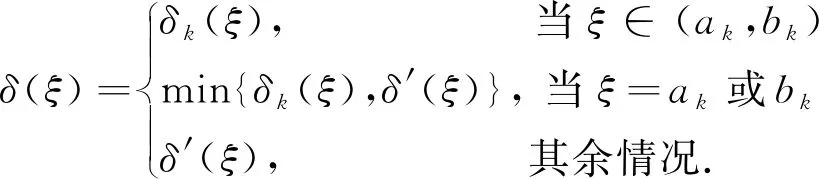
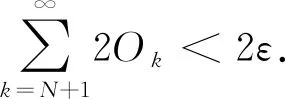
——基于菏澤市59所校園足球特色學(xué)校問卷調(diào)查*

