明確目標(biāo)是要務(wù) 先猜后證是良策

◇ 北京 范方兵 王芝平(特級教師)

解析幾何既是高考的重點,也是高考的難點.在解答解析幾何題目時,往往會在某一步中思路受阻,不知該如何往下進行,迷失了解題的方向,有時即使能繼續(xù)往下計算,運算量也非常大.因此,在解題中找到解題的目標(biāo)是首要任務(wù),目標(biāo)明確后,再考慮如何簡化運算.

我們知道,普遍性寓于特殊性之中,并通過特殊性表現(xiàn)出來,沒有特殊性就沒有普遍性,一個命題在一般情形下成立,那么它在特殊情形下也成立.為了明確解題目標(biāo)、降低運算量、提高運算速度,對具有一般性結(jié)論的題目,若能發(fā)現(xiàn)題設(shè)條件具有某種特殊的數(shù)量關(guān)系或所給圖形具有某種特征時,可選取恰當(dāng)?shù)奶厥庠?特殊點、特殊值、特殊圖形、特殊例子)進行簡單的運算、推理或判斷.

我們大致有兩個途徑來尋求解題目標(biāo):一是作出符合題目要求的示意圖,通過圖形的直觀性先猜后證,實際上,很多時候只要作出大致準(zhǔn)確的示意圖,其結(jié)論就不難猜測;二是從特殊情形去算一算,通過特殊情形的結(jié)論,猜測一般情形的結(jié)論.下面以一道高考試題來進行具體說明,希望對讀者有所幫助.

1 試題再現(xiàn)

題目(2020年全國卷Ⅰ文21理20)已知A,B分別為橢圓E的左、右頂點,G為E的上頂點,為直線x＝6上的動點,PA與E的另一交點為C,PB與E的另一交點為D.

(1)求E的方程;

(2)證明:直線CD過定點.

2 解法分析

(2)思路1設(shè)P(6,p),則直線PA的方程為

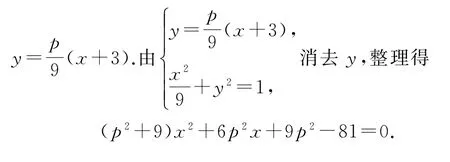
所以

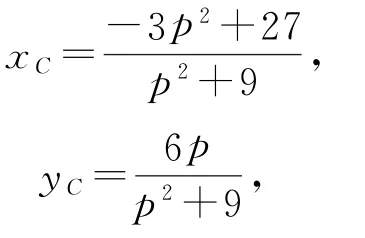
即

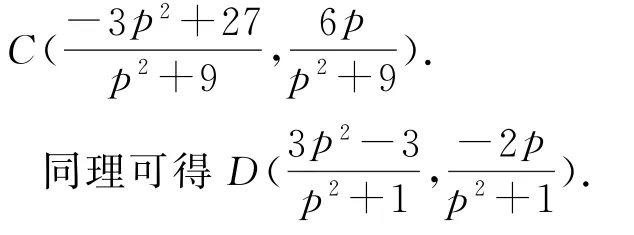
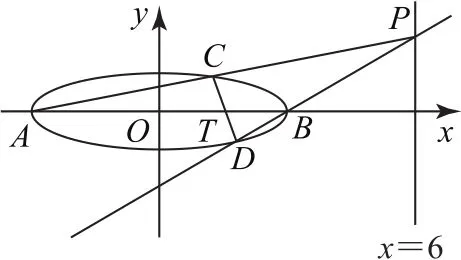
圖1

由對稱性可知,直線CD若過定點,則該定點必在x軸上.設(shè)定點為T(t,0),則

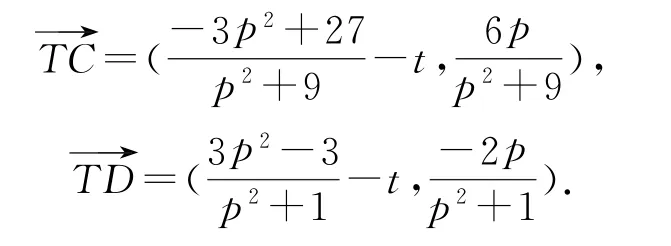
因為C,T,D三點共線,所以

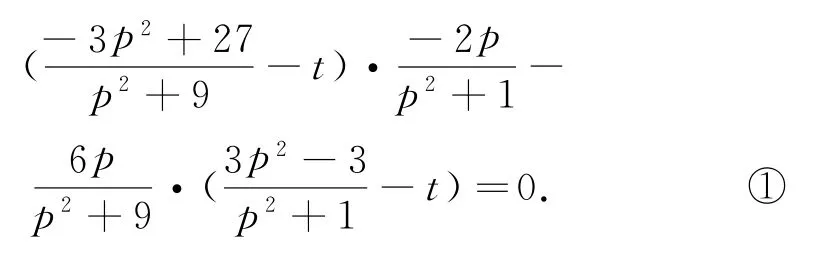
如果感覺上述方程比較難解,那么還有沒有別的方法呢?實際上,著眼于“特殊性探路,一般性證明”的思路,我們在式①中可以取p＝1,不難得到再證明時,式①成立,運算難度就降下來了.

思路2因為兩點確定一條直線,所以C,D兩點坐標(biāo)會滿足關(guān)于x,y的同一個一次方程,這個方程對應(yīng)的直線過定點即可.

設(shè)P(6,p),C(x1,y1),D(x2,y2).當(dāng)p≠0時,x1≠3,x2≠－3.因為A,C,P三點共線,所以kAC＝,得

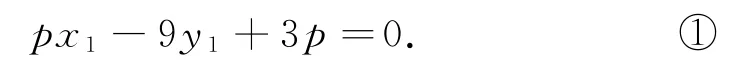
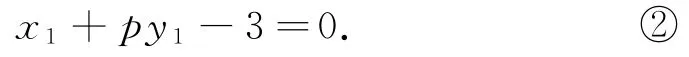
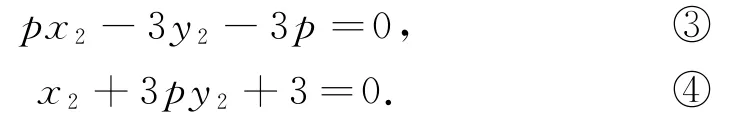
①②表示點C的坐標(biāo)所滿足的方程,③④表示點D的坐標(biāo)所滿足的方程.

同理,可以得到③×3＋④×p,得4px2＋(3p2－9)y2－6p＝0.因此,直線CD的方程為4px＋(3p2－9)y－6p＝0,恒過點.當(dāng)p＝0時,直線CD與x軸重合,必過點.

思路3設(shè)P(6,p),當(dāng)p≠0時,x1≠3,x2≠－3,y1≠y2.若x1≠x2,直線CD的方程為y－y1＝,整理得.

于是,只需要證明

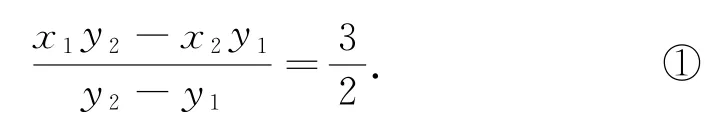
這是一個關(guān)于x1,x2,y1,y2的等式,我們希望利用點的坐標(biāo)對幾何關(guān)系的刻畫,來證得等式成立.

首先,我們刻畫點P是直線AC與BD的交點.

由A,C,P三點共線,知

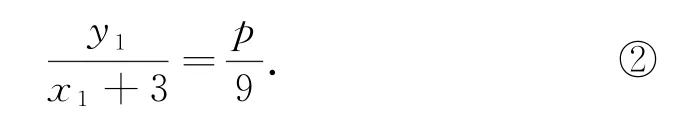
由D,B,P三點共線,知

因為①中只含x1,x2,y1,y2四個量,因此由式②③,消去p,得到整理得

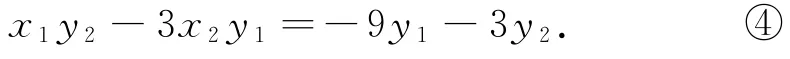
這個結(jié)果離①還有點遠,其原因是點C,D在橢圓上還沒有得到刻畫,于是我們就從這里入手.

3 解后反思

2)思路2中,在得到式①②③④后,如果沒有解題目標(biāo)“直線CD過定點的指引,那么下一步該干什么就會迷失方向,代數(shù)運算的難度也會很大,很可能會進行毫無目的的湊配.有了目標(biāo)的指引,既清晰了解題思路,又使得代數(shù)運算有了思維的固著點,是一種清晰、生動的思維活動,而不是煩瑣的嘗試,真正體現(xiàn)了“代數(shù)運算表其外,幾何性質(zhì)蘊其中”.

3)思路3也是基于對解題目標(biāo)“直線CD過定點”的探索、猜想,得到了待證目標(biāo)后面的代數(shù)變形都是圍繞這個目標(biāo)來進行,使得整個解題過程一氣呵成.本題考查學(xué)生動手探索、轉(zhuǎn)化與化歸的數(shù)學(xué)能力,在平時的教學(xué)中,教師要引導(dǎo)學(xué)生動手實踐,根據(jù)圖形直觀、特殊情形,對所求結(jié)論進行大膽猜想,從而明確解題目標(biāo),選擇簡捷、合理的方法進行推理、計算,真正讓學(xué)生體會在解析幾何解題過程中“明確目標(biāo)是要務(wù),先猜后證是良策”.

4)本題以射影幾何中有關(guān)極點、極線的理論為基礎(chǔ),背景深刻,設(shè)問精巧,考查解決解析幾何問題的一般思路與方法,考查數(shù)學(xué)運算、邏輯推理等數(shù)學(xué)核心素養(yǎng).本題也可以基于極點、極線的理論,在雙曲線、拋物線中進行結(jié)論的相應(yīng)拓展,限于篇幅,不再贅述.