教材分析從理解走向探究:尋找均值不等式鏈中的主線
2021-01-12 09:03:44葛慧敏徐章韜
數學通報
2020年12期
葛慧敏 徐章韜
(華中師范大學 數學與統計學學院 430079)
1 引言
下面是在教材深度分析中,通過探究來理解教材的一個案例.這個案例的作用不只是從另外一個角度理解均值不等式,而是為了闡明一種一線串通的思考路徑.
2 各種平均數的得來
2.1 算術平均數
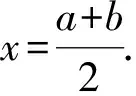
2.2 調和平均數
(1)變常數
(2)分式變換
進行倒數變換.倒數變換是代數變形中的一種常見技法.
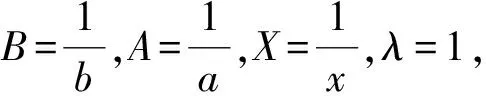
2.3 幾何平均數
(1)常數變易
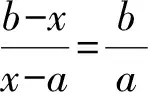
(2)變常數為未知數
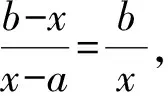
(3)分式變換
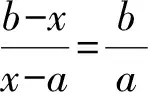
2.4 平方平均數
(1)常數變易
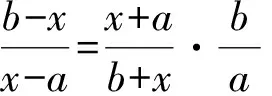
(2)分式變換
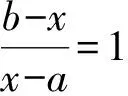
3 各種平均數的統一
3.1 引出凸、凹函數的概念
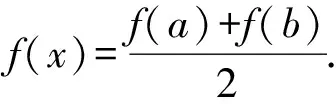
3.2 得到大小關系鏈
再由比例的性質有
故有Q>A>G>H.
3.3 從幾何上說明
古希臘人為了克服無理數的困擾,對線段比十分熱衷.平行線分線段成比例定理更是相似三角形的基礎.由此,可以得到上述不等式鏈的幾何說明.
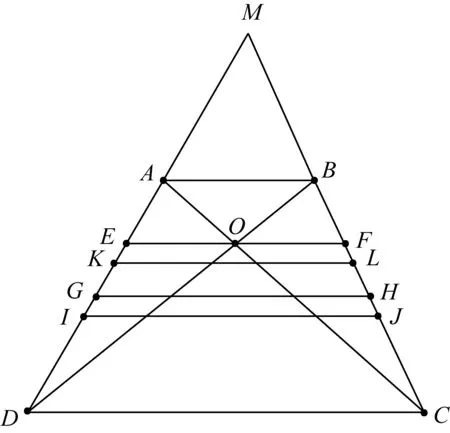
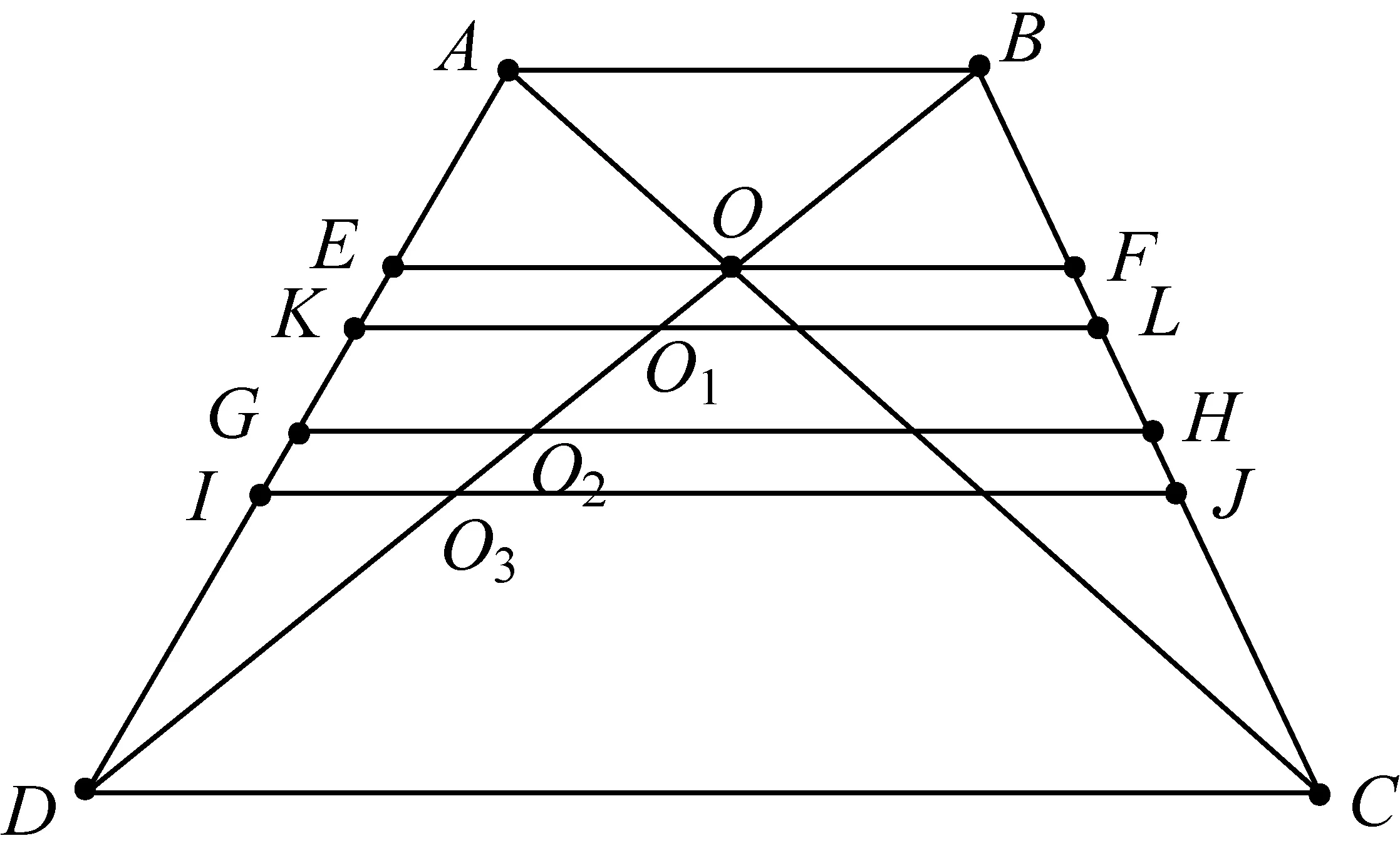
如圖1,四邊形ABCD為梯形,其中AB=a,DC=b(不妨設a 圖1 (1)分別計算線段EF,GH,KL,IJ的長度. ② 因為梯形ABLK∽梯形KLCD, ④ 如圖2計算IJ的長度,延長CB與DA交于點M. 圖2 (2)研究線段EF,GH,KL,IJ在梯形ABCD中的位置. 圖3 如圖3,設線段KL與線段BD交于點O1,線段GH與線段BD交于點O2,線段IJ與線段BD交于點O3. 在上述過程中能夠看到,采取的主體思路是:以定比分點公式為主線串通均值不等式鏈.通過算術平均數的定義引入定比分點公式的表示,猜想定比分點公式可以推導出調和平均數、幾何平均數和平方平均數;把握三種平均數的特點,利用常數變易和分式變換兩條變換路線進行推導;說明均值不等式鏈中的各種平均數都可以通過定比分點公式而得到.……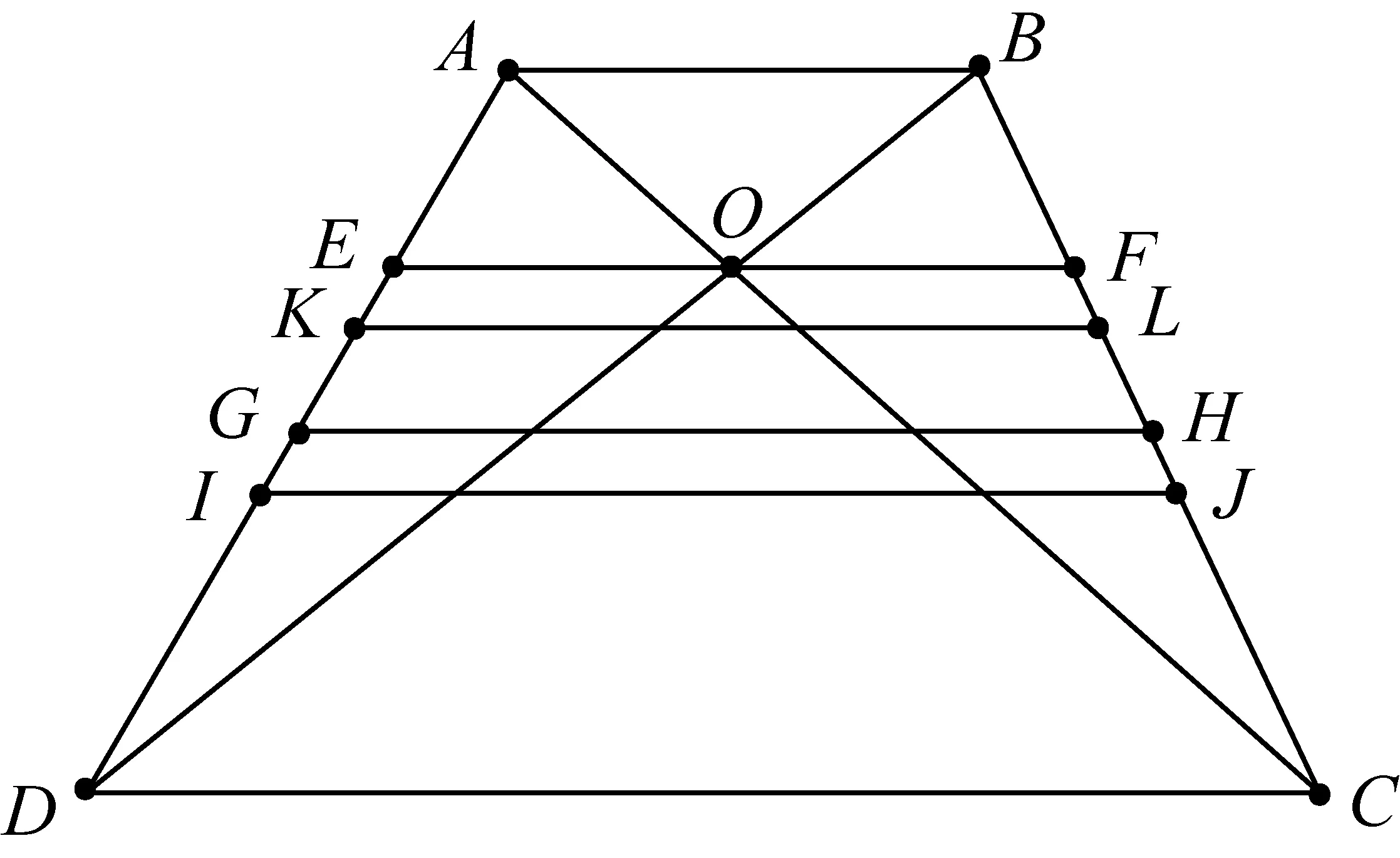

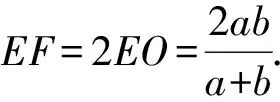
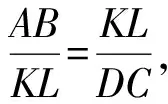

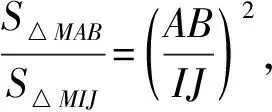
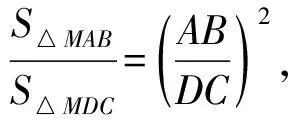
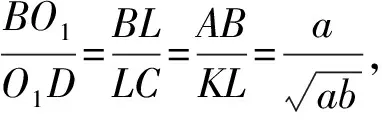
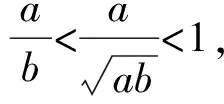
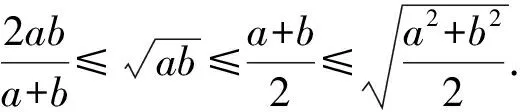
4 分析與討論
登錄APP查看全文
猜你喜歡
新世紀智能(英語備考)(2021年10期)2022-01-18 05:12:14
新世紀智能(英語備考)(2021年9期)2021-12-06 05:22:38
新世紀智能(英語備考)(2021年11期)2021-03-08 01:10:02
中等數學(2021年11期)2021-02-12 05:11:46
新世紀智能(英語備考)(2020年11期)2021-01-04 00:41:50
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

