高中數學解題中線性規劃的有效應用

徐 芹

(安徽省蕪湖市第十二中學 241000)

高中數學解題中，線性規劃的應用和解題是考試的熱點和難點，線性規劃是一種有效的解題輔助工具，在很多數學問題中廣泛使用，優化解題過程，提高學生解題效果和質量.作為高中數學教師，需要引導學生利用線性規劃解題，培養學生良好的解題意識，發揮線性規劃的優勢，明確數學問題解題思路，簡化數學解題計算，有效解答數學問題.結合具體的數學解題，引導學生掌握線性規劃應用技巧，不斷地歸納和總結，更好地利用線性規劃解決問題，提高學生解題能力.

一、線性規劃思想遷移，解決函數最值問題

高中數學教學中，函數知識是重要的內容，函數最值求解是函數解題的重點和難點，也是高考數學中常考的內容.在函數最值解題中，解題的方式有很多，應當根據題目特點，靈活選擇解題方式，保證解題效率.利用線性規劃解決函數最值問題，是一種有效的解題方式，特別是特殊的二元函數最值解題，降低問題解答難度，保證學生快速解決函數問題.

例1當a2+b2-4a+6b+11=0時，求a+b+4的最值.

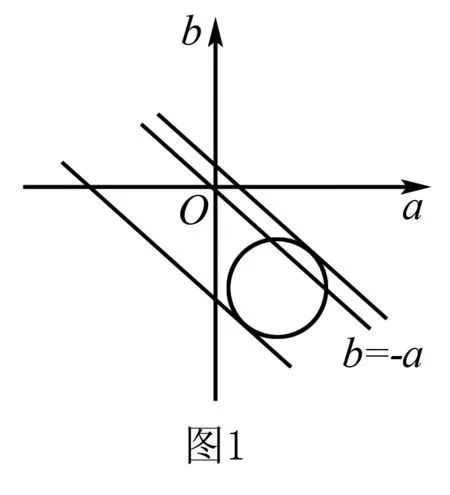
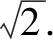
高中數學函數最值求解時，根據題目條件進行分析，借助數形轉化思想，靈活利用線性規劃方式，明確問題解題思路，保證題目有效解答.

二、有效利用線性規劃，解決數列問題

高中數學教學中，數列是重要的知識內容，其數學概念和公式比較多，數列問題解題難度比較大，也是高考數學考查的重要內容.數列范圍問題是數列問題中的典型問題，題目綜合性比較強，通常情況下常將數列范圍問題轉化成函數問題解題，但是，一些數列范圍問題不適合構造函數，影響學生解題.因此，教師可以引導學生將數列問題轉化成不等式問題，通過變形將原問題轉化成線性規劃問題，完成數學難題解答.

例2已知數列{an}為等差數列，Sn為數列的前n項和，S4≥10，S5≤15，求a4的最大值.

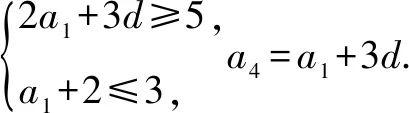
三、利用線性規劃，解決不等式問題

不等式是高中數學的重要內容，題目綜合性強，和方程、函數、概率等知識有著非常大的聯系.在部分不等式問題求解中，解題難度大，解題過程復雜，影響學生解題效率.在這樣的情況下，引導學生嘗試線性規劃解題，利用數形結合思想，將相關數量關系和信息直觀展示出來，使得解題更加簡便快捷，保證解題準確性和解題效率.

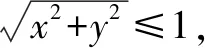
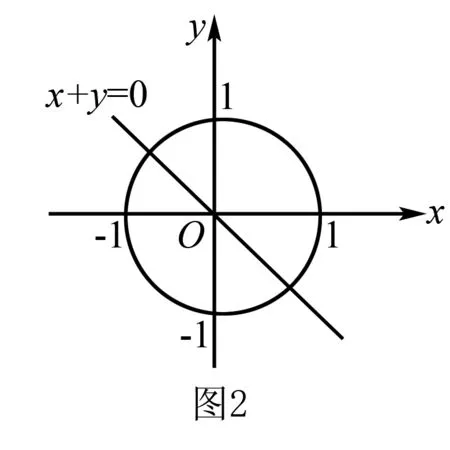
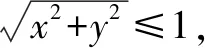
在解題的過程中，將不等式的轉換和獲得可行域是解題的關鍵，根據題目已知進行分析，通過相應的換元獲得可行域，將其轉化成線性規劃問題.此題要求學生具有比較強的思維能力，題目有著一定的深度，實現學生的全面考查.

四、利用線性規劃，解決向量問題

向量具有代數形式和幾何形式的雙重特點，將數與形融為一體.在向量問題解答中，從數的角度來說，其思路將幾何問題轉變成坐標和符號，結合坐標進行適當的變形處理，完成解答，也可以將其轉化成線性規劃問題，對題目進行思考和解答，保證學生解題效率和準確性，提高學生數學解題能力.

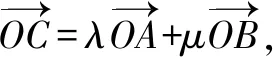
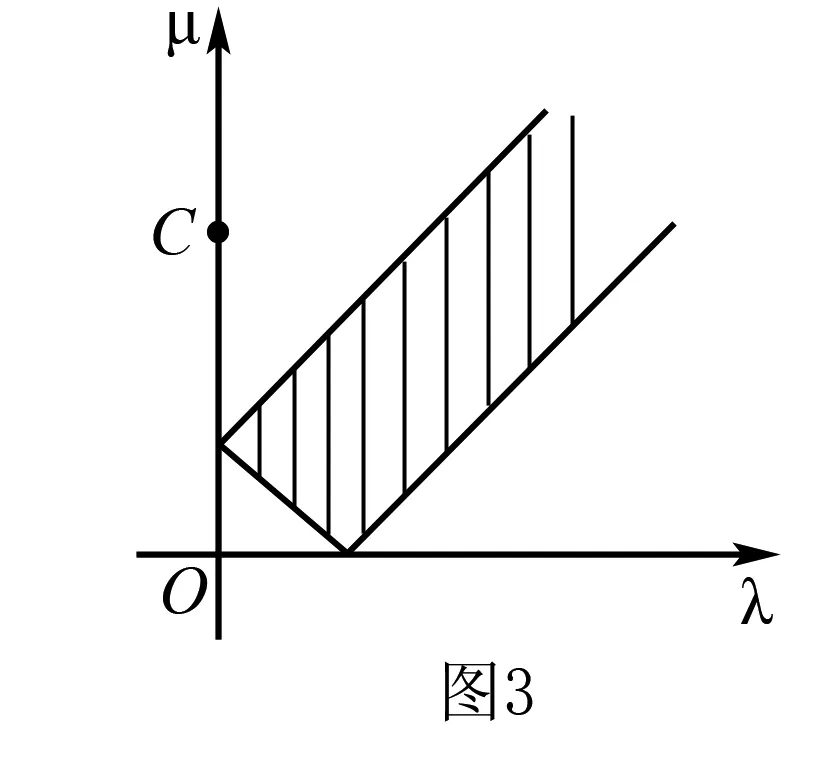
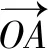
高中數學解題中，線性規劃應用比較廣發，通過線性規劃求解函數最值問題，解決平面幾何的相關數學問題.應用線性規劃解決數學問題，可以減少運算量，將抽象內容轉變成直觀圖形，化繁為簡，實現數學問題快速準確解答.作為高中數學教師，在解題中引導學生樹立數形思想，有效利用線性規劃，掌握有效的解題方式，巧妙解決數學難題，樹立學生學習自信心，提高學生解題能力.