2019年高考全國卷Ⅱ文科數學第20題深度賞析

潘敬貞 蔡海濤

(1.廣東省汕頭市澄海華僑中學 515800；2.福建省莆田第二中學 351131)

蔡海濤(1975-)，男，福建省莆田人，中學高級教師，從事高中數學教學研究.

每一道高考試題都是命題專家的智慧結晶，高考題不僅承載著選撥使命，還承載著引導教學、育人等多重使命.很多高考題的解法并不唯一，為不同考生提供了多樣的思考空間和解答路徑，在某種程度上體現了試題的人文關懷，更是命題專家智慧的體現.本文以2019年高考全國卷Ⅱ文數第20題為例，進行多解分析和變式探究，以期與同行交流.

一、試題呈現與分析

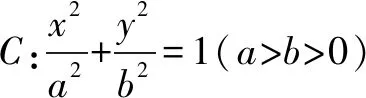
(1)若△POF2為等邊三角形，求C的離心率；

(2)如果存在點P,使PF1⊥PF2,且△F1PF2的面積等于16，求b的值和a的取值范圍.

本道的第一問是以橢圓的焦點三角形為背景，求橢圓的離心率，該問主要考查橢圓定義和基本性質，試題難度不大，很多學生都能夠輕松作答.第二問是以橢圓焦點三角形為研究背景，以三角形面積為研究對象，求橢圓的參數的值和范圍.該問主要考查橢圓基本性質，焦點三角形面積，直線與圓錐曲線的位置關系等知識，考查學生的推理論證與運算求解等能力，考查數形結合、化歸轉化及函數方程思想等數學思想方法，考查邏輯推理、直觀想象、數學運算等數學核心素養.

本道試題并不難，試題素材和問題設置學生并不陌生，提出的問題都是解析幾何中較為基礎、常規的問題.試題入口寬，層層遞進，有利于學生的解答.試題的解答最關鍵是通過直觀想象、數形結合等過程將題設的幾何條件轉化為代數進行處理，其解題智慧點是選擇恰當的化歸方式進行優化推理過程.試題突出以知識為載體，重點考查數學“四基”和“四能”，考查學生的核心素養水平.試題具有很好的信度與效度，對其進行求解探討和變式探究對提升學生解題能力，發展數學素養水平，提高備考效益等具有積極意義.

二、解法賞析

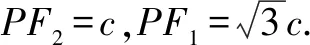
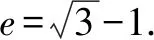
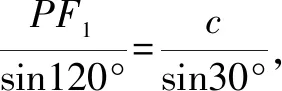
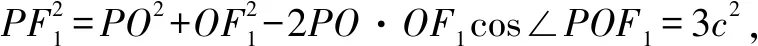
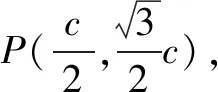
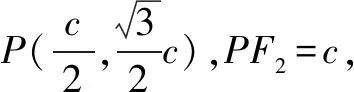
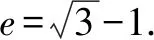
評注解法1—解法4其本質是一樣的，都是圍繞焦點三角形進行求解.解法1與解法2通過連接PF1后根據直角三角形的性質得△PF1F2是直角三角形，再結合橢圓定義進行求得橢圓的離心率，解答思路簡單、過程簡潔，這兩種解法是解答該題的最佳解法.解法3和解法4連接PF1后在△POF2中利用正余弦定理求得PF1，再結合橢圓定義也可求得橢圓的離心率，這兩種解法的解答過程也不是很復雜，若一時沒想到△PF1F2是直角三角形，解法3和解法4也是不錯的選擇.解法5是將點P的坐標代入橢圓方程得出關于a，b，c的方程，再結合b2=a2-c2即可求出橢圓的離心率，該解法自然，思路清晰，但對運算求解能力的要求相對較高.解法6是利用橢圓的第二定義，雖然教材沒有專門介紹橢圓第二定義，但教材例題蘊藏著該方法，該解法的解答思路清晰、過程簡潔，解答小題用該解法達到快速、高效的目的.

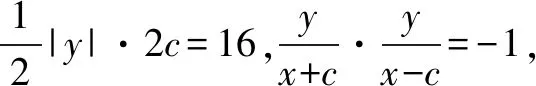
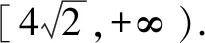
評注解法1是通過設點P的坐標，然后根據題意列出相關的方程并求解得b的值，再通過代數變形以及不等關系a的取值范圍.該解法解題思路清晰，容易想到，但對運算求解能力和推理論證能力的要求比較高.

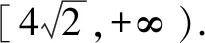
評注解法2主要利用橢圓定義、三角形面積公式、勾股定理列有關方程，然后結合橢圓中基本量的關系解得b的值，最后利用基本不等式求得a的取值范圍.該解法的思路也非常清晰，也是容易想到的解法，同時減少了運算量，是該題的通解.

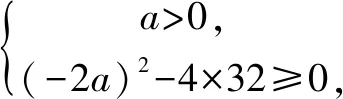
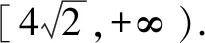
評注該解法思路清晰，運算量小，過程簡潔、高效.該解法的巧妙之處是將方程思想使用得淋漓盡致.

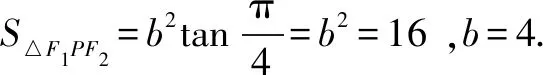
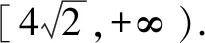
評注該解法用到焦點三角形面積的結論快速求出b的值，再利用數形結合很快解得a的取值范圍，但需要注意的是，在解答題的解答過程中焦點三角形面積的結論不能直接使用，需要有解答、推理過程.但若在解答客觀題時該解法是很不錯的選擇，可以快速準確的解決問題.

三、變式探究

情景變式和過程變式是試題變式的重要路徑，這兩種變式都有利于揭示問題的本質，拓展問題的外延，對培育學生的數學能力，發展學生的核心素養水平都大有裨益.

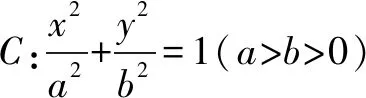
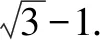
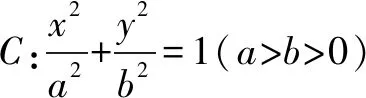
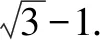
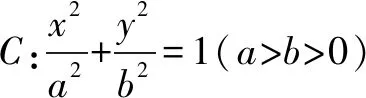
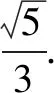
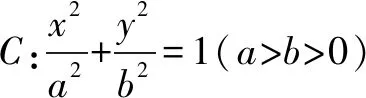
變式5 已知長方形ABCD，AB=4，BC=3，則以A、B為焦點且過C、D兩點的橢圓的離心率是____.

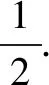
評注變式1——變式5都是對考題的第一問進行情景變式，將問題的情景和表述進行變換，但問題的本質是相同的，求解思路基本一致.通過對變式1——變式5的求解讓學生在變中尋找不變的本質，加深學生對問題本質的理解，提高審題能力、分析問題能力、解決問題能力，提升學生的數學思維能力、應變能力等.

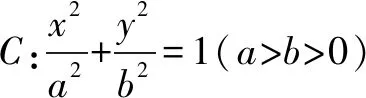
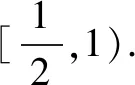
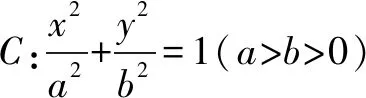
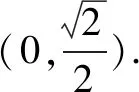
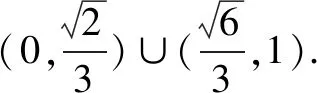
評注考題的第二問是通過已知焦點三角形的面積告知參數b的值，橢圓上存在點P使PF1⊥PF2告知參數a的取值范圍.變式6——變式8是在考題第一問的基礎上結合第二問的思路，進一步研究橢圓的性質.變式6——變式8的求解思路從方程思想到尋找不等式關系，試題難度進一步提高，問題的求解對數學能力的要求進一步提高.通過對變式6——變式8的求解進一步提高學生的分析問題能力、解決問題能力，最終提高學生的數學能力，發展學生數學素養水平.

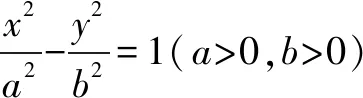
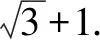
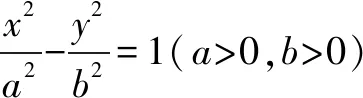
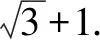
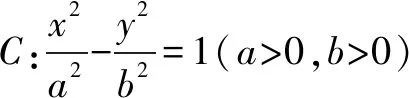
答案：2.

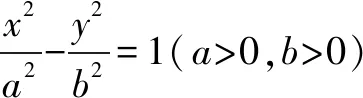
答案：[2,+∞).

評注變式9——變式12是切換問題背景，將橢圓換位為雙曲線，為一般化研究進行有益探索，同時也為學生應用實踐提供有效的素材，對提高學生的分析問題能力和解決問題能力，提高復習備考效益有積極意義.

高考試題具有導向功能，做為一線教師需細細口味，從不同角度對試題進行深度賞析，引導學生對問題本質加深理解，打通知識脈絡，編織知識網絡，構建知識體系.同時，教師對問題進行情景變式探究，可讓學生在變的過程中尋找不變的本質，有利于揭示問題本質；而過程變式探究可引導學生深度學習，拓寬解題思路，訓練數學思維，提升數學能力，發展數學素養水平等，從而讓學生在解題實踐中深化對知識的理解，在解決問題過程中提升數學素養.