運用題組化的比對訓練提高高三數學復習效率

楊偉達

(廣東省廣州市花都區第二中學 510820)

一、相近比對，避免學生“定勢思維”，減少錯誤發生

在集備編寫題組時，基于不同學生不同思維，備課組各成員以課本例題、習題為藍本，編寫一些有針對性的變式練習.如果僅僅就題論題，學生容易產生厭倦，勢必造成定勢思維. 誠然，用同樣的方法去解決近似題，這種套路常常起到快速解題的效果，但對貌合神離的同類題，有時一不小心，就會容易導致誤解、錯解，因此在集備討論時有必要把它羅列出來，在課堂教學中給學生一個警醒.

在高三數學教學中，為了避免定勢思維給學生帶來的不利影響，筆者編制如下相近題組進行比對訓練，減少錯誤發生.

片段1：(1)若函數f(x)=x2-mx+1的遞減區間為(-∞，2)，求m的取值范圍.

答案：m=4

(2)若函數f(x)=x2-mx+1在(-∞，2)上為減函數，求m的取值范圍.

答案：m≥4

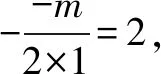
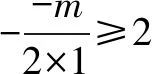
上述“形相近意相遠”的近似題組，通過題組化的比對訓練，有效防止定勢思維在解題中的負面影響.

二、易錯比對，避免學生再次犯錯

在集備編寫題組時，備課組各成員根據學生心理認知規律，針對學生易犯、常犯的知識點，通過變條件、變結論設計易錯題組進行比對訓練，可有效地避免學生一錯再錯.比如，針對學生求任意角三角函數值時容易出錯，筆者可編制易錯題組，通過易錯比對，有效幫助學生避免再次犯錯.

片段2：(1)已知角α的終邊經過點P(3,-4)，求sinα.

(2)已知角α的終邊經過點P(3a,4a)(a≠0)，求sinα.

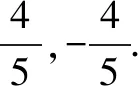
易錯點：對a進行分類討論(1)a>0，(2)a<0.

答案:-4.

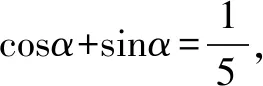
三、設疑比對，拓寬學生思維的廣度、深度

在集備編寫題組時，教師根據以往的教學經驗或教學筆錄，先預設學生的可疑處，在可疑處設計不同的題組，讓不同的學生從不同的角度理解知識的本源，從而提高學生解決問題的能力.例如在弧度制概念課時，筆者針對學生在弧度制與角度制之間互化中有困惑，以此進行設計，通過比對訓練，學生對弧度制的概念及運用有了全新的認識.

片段3：(1)扇形的弧長是16，半徑為2，求扇形的面積.

(2)扇形的弧長是16，圓心角是2弧度，求扇形的面積.

(3)扇形的弧長是16，圓心角是30°，求扇形的面積.

(4)扇形的周長是16，圓心角是2弧度，求扇形的面積.

(5)扇形的弧長是16，圓周角是2弧度，求扇形的面積.

(8)扇形的弧長是16，圓心角α滿足tanα=1，求扇形的面積.

(9)扇形的周長是16，求扇形的面積的最大值.

(10)扇形的弧長是16，當圓心角為多少弧度時扇形的面積最大？

(11)扇形的面積是16，求扇形周長的最小值.

上述題組，通過比對設疑，把半徑、弧長、周長、面積概念呈現一遍，在弧度制與角度制互化中做文章，從而揭示問題的核心，復習效率就會有質的飛躍.

因此，在編寫題組時，為了加深對所復習知識的理解和掌握，筆者通過編寫恰當的題組把學生的疑問引向深入，從課內到課外，幫助學生提高認識、拓寬思維，從而提高學生的數學素養.

四、層次比對，提高學生學習數學的參與度，讓不同學生都有收獲

眾所周知，集體備課是中小學教師走進課堂的必備條件，也是許多學校一項常規的重點工作，一直圍繞“誰來備”、“備什么”、“如何備”等環節開展活動. 所以在集備時以什么資料作為藍本編寫例題，確保題組內容從易到難，讓不同認知水平的學生都能參與思考,有所收獲，從中受益.這種層次比對變式教學，引導學生由淺入深、層層分解，引導學生找到破解問題的方法，對提高數學課堂效率會有較大的幫助.

例如，人教版必修4第124頁兩角差的余弦公式cos(α±β),為鞏固此公式，筆者可設計如下題組加以分層比對.

片段4：第一層次 公式正用，簡單模仿，“途”、“改”運算

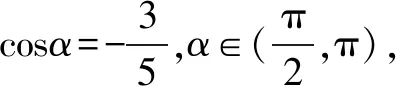
(2)求cos15°值.

第二層次 公式逆用，限兩角，促轉化

(1)cos72°cos12°+sin72°sin12°;

(2)sin34°sin26°-cos34°cos26°;

(3)cos74°cos104°+sin74°sin76°;

提示：3角化2角

(4)cos74°cos104°+sin106°sin76°.

提示：4角化2角

第三層次 公式逆用，轉結構，限兩角，促轉化

(1)sin70°sin10°+cos70°sin110°;

提示：大角化小角，3角化2角

(2)sin50°sin20°-sin140°sin290°;

提示：大角化小角，4角化2角

(3)cos(α+β)cosα+sin(α+β)sinα;

提示：復合角加減

(4)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β).

提示：復合角加減 -cos(α-γ)

上述設計層層遞進,每做完一題組,適時提示學生解決這類問題的要點(兩個角和差、結構),就會讓學生有意識朝這個方向思考，使得不同學生都有收獲，從而調動學生的學習積極性.俗話說：“沒有調查就沒有發言權.”教師根據以往教學經驗或筆錄，在教學中有目的、有針對性地運用題組化比對教學，就能大大提高高三數學復習效率.

在題組化的比對教學中，無論是從數量上還是從質量上都要有度，題目過多就成題海，過深就會超出學生的接受能力，成為廢題，教學效果就會大打折扣.只有題量適度，難度適中，各題間又有層次性，這種題組化的比對訓練，才能達到鞏固知識、提升能力、促使教學目標高效完成.實踐證明，題組化的比對訓練，能明顯提高課堂的教學效率，能有效地減少學生的學習負擔，在高三數學復習中起到四兩拔千斤的效果.