截口橢圓離心率問(wèn)題的探究

康 琳

(四川師范大學(xué)附屬中學(xué) 610061)

題目設(shè)圓錐的軸截面是一個(gè)正三角形,用一個(gè)與圓錐底面成30°夾角的平面去截圓錐,所得截口曲線是橢圓,則該橢圓的離心率為_(kāi)___.

思路1確定橢圓上特殊點(diǎn)的坐標(biāo)

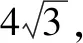
思路2橢圓短軸所在的圓截面上利用勾股定理計(jì)算短半軸長(zhǎng)

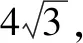
思路3構(gòu)造三角形，利用相似計(jì)算短半軸長(zhǎng)

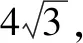
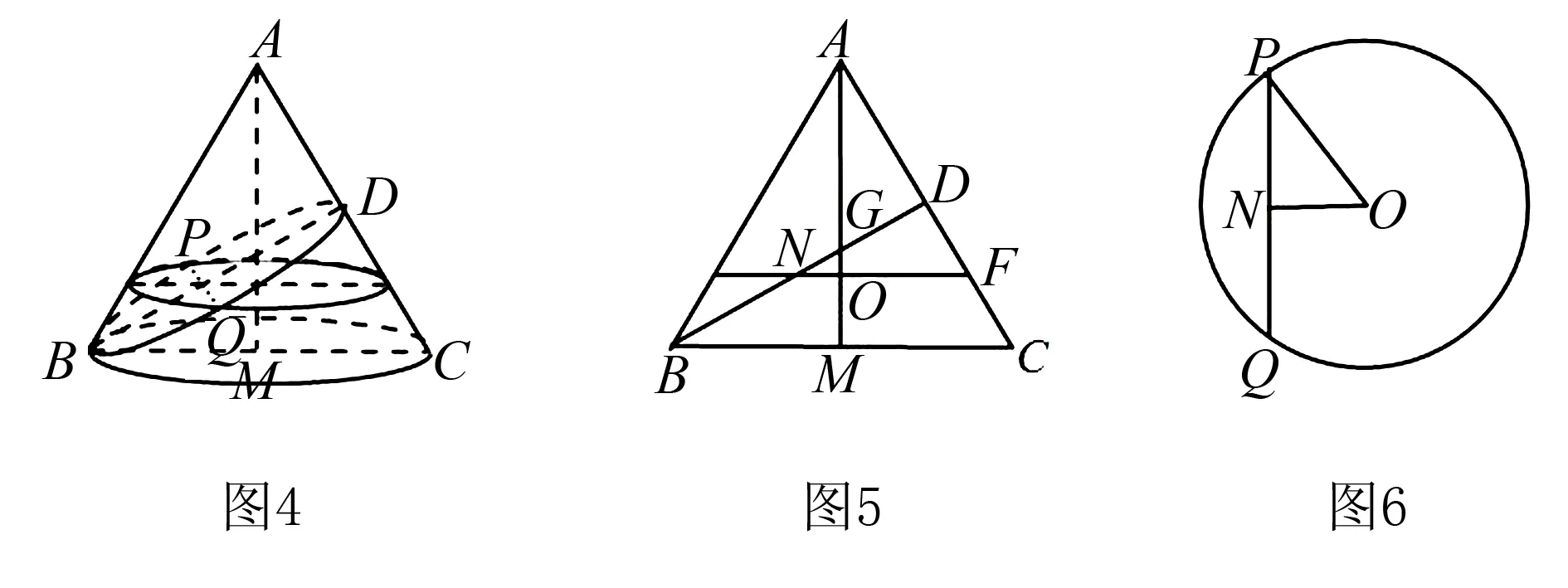
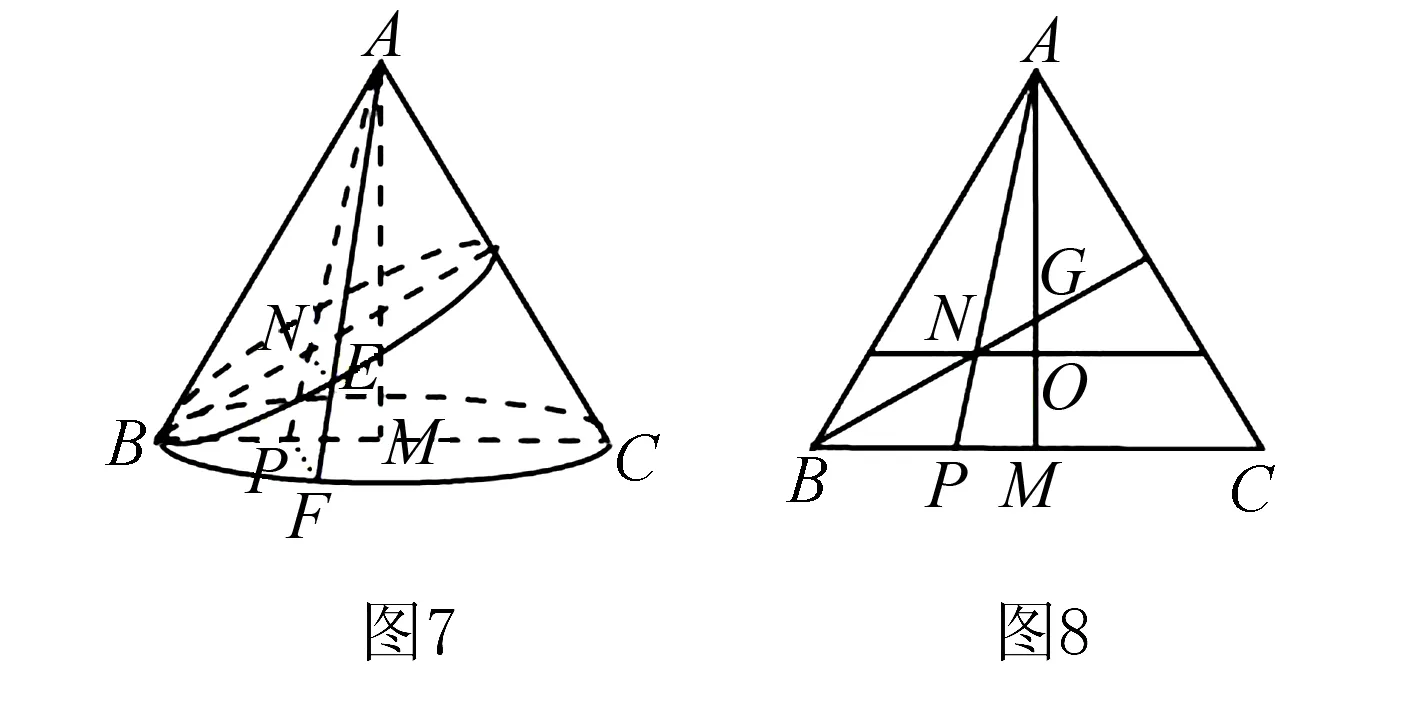
思路4構(gòu)造直角三角形，利用勾股定理計(jì)算短半軸長(zhǎng).

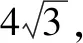
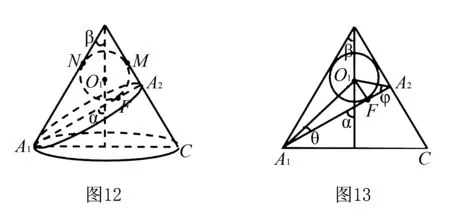
思路5利用Dandelin球與截面、側(cè)面相切，切點(diǎn)為焦點(diǎn)

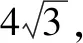
點(diǎn)評(píng)以上五種思路都充分利用了特殊的幾何關(guān)系，特別是條件里的正三角形使計(jì)算比較容易，如果將題目中軸截面改為等腰三角形(非正三角形)，夾角非特殊角度時(shí)，幾何關(guān)系的不明確將增加運(yùn)算難度，甚至運(yùn)算難以進(jìn)行，于是產(chǎn)生了對(duì)這道題的進(jìn)一步探究.

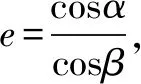
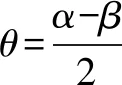
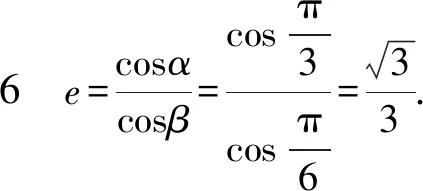
點(diǎn)評(píng)用此公式求截口曲線——橢圓的離心率不僅快捷，而且更具有普適性.

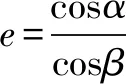
小結(jié)本文的題目以“截面橢圓”為載體，既考查了學(xué)生直觀想象的核心素養(yǎng)，也考查了數(shù)學(xué)抽象的核心素養(yǎng)，在這個(gè)過(guò)程中，還需要學(xué)生具備較強(qiáng)的邏輯推理能力和數(shù)學(xué)運(yùn)算的能力；就這個(gè)題目而言，以上多種思路需要用到數(shù)形結(jié)合的思想，化歸及轉(zhuǎn)化的思想.同時(shí)也揭示了平面解析幾何的本質(zhì)思想—幾何問(wèn)題代數(shù)化.這強(qiáng)調(diào)了知識(shí)的交叉，滲透和綜合，因此，這個(gè)題目的綜合性較強(qiáng)，是立體幾何與平面解析幾何綜合考查的典范，極具探究意義.