奇偶性在高考中的應用

陳建會

(河北省滄州市海興縣中學 061200)

一、結合奇偶性確定函數類型

分析結合冪函數f(x)=xα為奇函數，且在(0，+∞)上遞減，利用冪函數的基本性質確定參數α所滿足的條件，進而結合題目中參數給出的已知值，求出相應α的值，得以正確確定冪函數的類型.

點評結合函數的奇偶性來確定函數的基本類型問題，關鍵是熟練掌握基本初等函數(指數函數、對數函數、冪函數等)的圖象與性質，特別要注意的是對應的參數值與相應的性質之間的關系.

二、結合奇偶性確定參數值

例2(2019·全國Ⅱ卷理·14)已知f(x)是奇函數，且當x<0時，f(x)=-eax.若f(ln2)=8，則a=____.

分析結合函數的奇偶性確定f(-ln2)的值，并借助對應的函數的解析式建立相應的關系式，通過求解方程來確定相應的參數值.

解析由于f(x)是奇函數，則知f(-ln2)=-f(ln2)=-8.又當x<0時，f(x)=-eax，則有f(-ln2)=-e-aln2=-8，即-aln2=ln8，得a=-3，故填答案：-3.

點評結合函數的奇偶性來確定相應的參數值問題，關鍵是根據題條件，利用函數的奇偶性建立起相應的方程或對應的關系式，進而通過求解相應的方程或對應的關系式來達到確定參數值的目的.

三、結合奇偶性確定解析式

例3(2019·全國Ⅱ文·6)設f(x)為奇函數，且當x≥0時，f(x)=ex-1，則當x<0時，f(x)=( ).

A.e-x-1 B.e-x+1 C.-e-x-1 D.-e-x+1

分析結合函數的奇函數的定義得到f(-x)=-f(x)，通過已知解析式的轉化加以確定當x<0時f(x)的解析式問題，進而得以正確判斷.

解析由于f(x)是奇函數，所以當x<0時，-x>0，可得f(-x)=e-x-1=-f(x)，即f(x)=-e-x+1，故選擇答案：D.

點評結合函數的奇偶性的定義以及不同條件下函數的解析式問題來確定相應的解析式問題，關鍵是正確掌握函數的奇偶性及其關系.解決此類問題特別要注意解析式中的符號，不要產生混淆.

四、結合奇偶性確定函數圖象

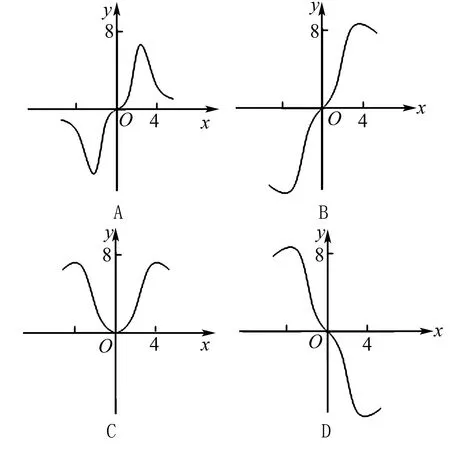
分析結合函數的解析式以及函數奇偶性的定義判斷已知函數的奇偶性問題，進而利用函數圖象的對稱性來排除相關的選項；再結合f(4)、f(6)的特殊取值情況繼續排除相關的選項，從而得以正確判斷.

故選擇答案：B.

點評結合函數的奇偶性來判斷函數圖象問題，往往通過函數的解析式并結合奇偶性的定義先確定其奇偶性，從而確定函數圖象的對稱性，再結合函數的其他基本性質、特殊點處的取值情況等來分析與判斷.

五、結合奇偶性與單調性交匯

例5(2019·全國Ⅲ卷理·11；文·12)設f(x)是定義域為R的偶函數，且在(0，+∞)單調遞減，則( ).

分析結合抽象函數的奇偶性加以轉化，關鍵是通過奇偶性把對應的函數值轉化為同一單調區間內，再借助復合函數的單調性性質，結合指數式與對數式的大小關系，進而達到判斷代數式的大小關系.

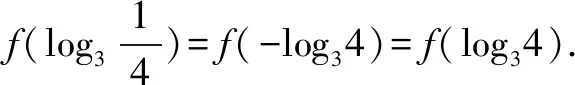
點評結合函數的奇偶性與單調性交匯來處理函數值的大小比較問題，經常借助指數函數、冪函數、對數函數等基本初等函數的圖象與性質，以及對應的指數冪運算、對數運算等相關內容，融合“函數”與“圖象”加以數形結合，是高考中比較熱點的一類常見題型.

六、結合奇偶性與周期性交匯

例6(2018·全國Ⅱ文·12；理·11)已知f(x)是定義域為(-∞，+∞)的奇函數，滿足f(1-x)=f(1+x).若f(1)=2，則f(1)+f(2)+f(3)+…+f(50)=( ).

A.-50 B.0 C.2 D.50

分析結合抽象函數的奇偶性與已知函數關系式，通過變形與轉化來確定函數的周期性，再綜合利用奇偶性與周期性的交匯知識，先確定一個周期內相應的函數值，再結合周期性特征來解決相應的函數值的求解問題.

解析由于f(x)是定義域為(-∞，+∞)的奇函數，且滿足f(1-x)=f(1+x)，可得f(x+1)=f(1-x)=-f(x-1)，則有f(x+4)=-f(x+2)=f(x)，則知函數f(x)的周期為T=4.由f(x+1)=-f(x-1)，及f(1)=2，可得f(3)=-f(1)=-2.又f(2)=f(-2)=-f(2)，則有f(2)=0，可得f(4)=-f(2)=0.那么f(1)+f(2)+f(3)+f(4)=0，所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2，故選擇答案：C.

點評結合函數的奇偶性與周期性交匯知識來綜合考查函數的求值問題，破解問題的關鍵是巧妙綜合利用奇偶性及周期性進行合理轉化與變換，進而將所求解的函數值的自變量轉化到已知解析式的函數定義域內來分析與求解.

歷年高考都對函數內容進行重點考查，往往都離不開函數的奇偶性，此類考題經常冪函數、指數函數和對數函數等為背景，綜合基本初等函數的圖象與性質以及相關的運算，有時單獨考查奇數性問題，有時綜合考查奇偶性與其他相關性質的交匯問題，這一類試題出現在小題(選擇題或填空題)中，難度屬于較易型或中等型.