三角平幾齊飛舞 解幾代數顯神通

柳朝輝

(湖南省岳陽臨湘市第一中學 414300)

一、典型題目

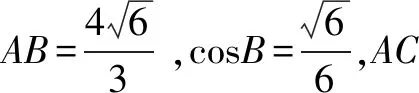
二、試題分析

這兩道題目都不是常規(guī)的解三角形問題，也許題目有三個甚至是四個條件，但是對于每一個三角形而言，又都沒有三個條件，所以每一個三角形都不是“可解三角形”.但方法選擇適當，則可以求解，也許還大大減少計算量，反之，一籌莫展.

三、解法探究

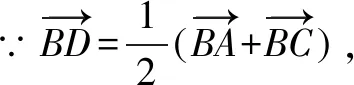
分析二因為有中線，所以聯想到作輔助線中位線.

分析三用倍長中線法把分散的條件集中起來.

方法三如圖4，延長BD至E，使得DE=BD，連接CE,AE，則四邊形ABCE為平行四邊形.

∴AE=2=BC.(以下同法一)

分析四用分割的方法，求出圖形中的各邊.

方法四如圖5，延長BD至P，使DP=BD，連接AP,CP得平行四邊形ABCP.過點A作AH⊥BC,過P點作PN⊥BC.

在直角三角形BNP中,BP2=BN2+NP2,

分析五用分割的方法.

方法五如圖5，作AH⊥BC，DQ⊥BC.

分析六建系求解.

方法六如圖7建系,則

一是全力推進“最多跑一次”改革。制定《全省國土資源系統(tǒng)加快推進“最多跑一次”改革實施方案》，開展全省國土資源行政審批事項標準化、格式化和規(guī)范化建設，規(guī)范“辦事清單+辦事流程+辦事指南”作為全省國土資源“最多跑一次”改革的重要內容。實現“最多跑一次”事項100%全覆蓋。依法清理證明材料和不相適應的規(guī)章和規(guī)范性文件；不斷優(yōu)化辦理流程，提高辦事效率。

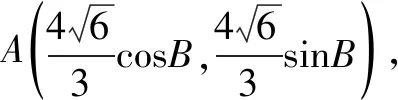
令C(x,0)，則中點

例2分析一利用平面幾何構造“X”型相似，把分散的條件集中起來.

分析二利用平面幾何作輔助線，構造“A”型相似.

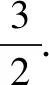
分析三運用“方程組思想”.

方法三在△ABD中，由正弦定理可知：

在△ADC中，由正弦定理可知：

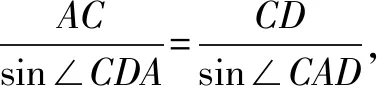
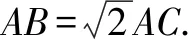
分析五運用“方程組思想”.

方法五在△ABC和△ACD中，由正弦定理可知：

四、總結提升

總之，八仙過海，各顯神通，一切知識可以“拿來主義”為我所用，數學知識到了頂層就可以說界線模糊.波得亞說過：中學數學教學的首要任務是加強解題訓練，但是數學老師如何才能讓數學教學不掉入“題海”之中，關鍵在于對問題的全面深入研究，教給學生解決問題的本質，思路的來源，讓一切奇思妙想有跡可循，順理成章.讓思考成為學生的技能，讓學生熟練運用自主思考.這樣學生才可以舉一反三，觸類旁通，達到“做一個，會一片，懂一類”，這樣才能保證教學的有效性.