高中數(shù)學(xué)函數(shù)教學(xué)中化歸思想的應(yīng)用研究

趙得兵

(青海師范大學(xué)附屬第三實驗中學(xué) 810105)

高中數(shù)學(xué)的學(xué)習(xí)中，將難以解決、難以理解的相關(guān)數(shù)學(xué)問題轉(zhuǎn)變?yōu)槿菀桌斫狻⒑唵巍⒁颜莆战鉀Q相關(guān)方法的問題，該解決問題的思維方式也就是化歸思想.其最明顯的特點就是具有規(guī)范性與模式性，把無法理解的新問題逐漸轉(zhuǎn)變成已經(jīng)掌握了解決方法的問題，從而得到相應(yīng)的結(jié)果.當(dāng)學(xué)生遇到無法預(yù)知的相關(guān)問題時，就可以對問題實施相應(yīng)的轉(zhuǎn)化，轉(zhuǎn)化成已掌握的解決方法的問題，這通常有利于學(xué)生通過已具備的知識，找出最清晰、最有效的解決方法，以防止不必要狀況的發(fā)生.將化歸思想運(yùn)用于數(shù)學(xué)學(xué)習(xí)時，其通過數(shù)學(xué)問題的轉(zhuǎn)化處理，將數(shù)學(xué)問題中的關(guān)鍵因素找出來，并化歸出其本質(zhì)，從而使學(xué)生清楚地了解到數(shù)學(xué)問題間存在的關(guān)聯(lián)，并促使學(xué)生有效解決相關(guān)數(shù)學(xué)難題.

一、化歸思想應(yīng)用于高中數(shù)學(xué)函數(shù)的作用

1.深化掌握函數(shù)知識

高中階段的數(shù)學(xué)知識中，數(shù)學(xué)函數(shù)不僅是學(xué)生學(xué)習(xí)的重中之重，而且還是學(xué)生學(xué)習(xí)的難點，數(shù)學(xué)教師想要使學(xué)生更好的掌握函數(shù)知識及其問題，就需想到多種解決方法.而化歸思想和函數(shù)相結(jié)合，通常對學(xué)生在學(xué)習(xí)中解決實際問題有著顯著的指導(dǎo)作用.例如，方程、幾何、函數(shù)的學(xué)習(xí)中能充分呈現(xiàn)出化歸思想.因此，數(shù)學(xué)教師可通過化歸思想，深化對函數(shù)知識的規(guī)律以及重難點知識的掌握，并加以學(xué)習(xí)總結(jié)，這不僅能加深學(xué)生對化歸思想的領(lǐng)悟，而且還能對數(shù)學(xué)知識進(jìn)行系統(tǒng)化掌握.

2.數(shù)學(xué)思維的培養(yǎng)

學(xué)生在解決函數(shù)問題時，化歸思想的合理應(yīng)用，不僅能開闊學(xué)生的解題思路，而且還能深化學(xué)生對相關(guān)問題的了解.高中數(shù)學(xué)的函數(shù)學(xué)習(xí)時，教師需注重化歸思想的深刻領(lǐng)會，將其與數(shù)學(xué)函數(shù)相結(jié)合，以此在復(fù)雜的函數(shù)知識當(dāng)中找到規(guī)律，并實現(xiàn)解題效率的提高，從而使學(xué)生形成相應(yīng)的思維習(xí)慣.

3.數(shù)學(xué)函數(shù)分析能力的提高

高中數(shù)學(xué)的函數(shù)學(xué)習(xí)中，教師需有目的、有目標(biāo)地培養(yǎng)學(xué)生具備的思維方式與綜合能力，強(qiáng)化學(xué)生對函數(shù)知識的分析能力，并在遇到問題時，可通過化歸思想的運(yùn)用，使復(fù)雜難解的問題實現(xiàn)簡單化，并使學(xué)生更準(zhǔn)確的看待問題，以成功地找出解題思路，并使解題正確率得以有效提高.

二、高中數(shù)學(xué)函數(shù)教學(xué)中化歸思想的應(yīng)用

1.對問題實施換元思考

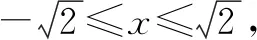
2.函數(shù)與圖形、正反向問題的轉(zhuǎn)化

首先，函數(shù)與圖形的問題，其通常是學(xué)生學(xué)習(xí)函數(shù)知識中很容易忽視的問題，如在解題當(dāng)中學(xué)生通常會忽視圖形的重要性，通過簡單的繪圖，將函數(shù)與圖畫相結(jié)合實現(xiàn)問題的解答.但是，如果對函數(shù)單調(diào)性開展教學(xué)時，可通過區(qū)間當(dāng)中有代表性的幾個點實施繪圖，并以此獲得函數(shù)單調(diào)性.因此，數(shù)學(xué)知識的學(xué)習(xí)中，通過團(tuán)體自己圖形相結(jié)合的方式，可以使解題的困難得到有效簡化，并使學(xué)生經(jīng)過圖象解讀，實現(xiàn)自身空間立體度與想象能力的提高，從而使學(xué)生學(xué)習(xí)函數(shù)的難度有效降低，并增強(qiáng)學(xué)習(xí)函數(shù)知識的自信，使學(xué)生對數(shù)學(xué)函數(shù)進(jìn)行解決的綜合能力得到有效提高.其次高中數(shù)學(xué)的函數(shù)學(xué)習(xí)中，通常會出現(xiàn)無法解決的問題，致使許多學(xué)生對解題喪失信心.當(dāng)學(xué)生遇到相關(guān)問題的時候，教師就需引導(dǎo)學(xué)生排除已有的條件，積極跳出當(dāng)前圈子，證明相反的方向是錯誤的，這就從另一個角度證明是正確的.因此，高中數(shù)學(xué)的函數(shù)解題中，不論是適合數(shù)圖結(jié)合的，還是正反問題轉(zhuǎn)化的解題方法，其都屬于化歸思想實施解題中的重要思路，該解題方式，不僅可以使學(xué)生的解題效率得到有效提高，而且還能使學(xué)生學(xué)習(xí)數(shù)學(xué)函數(shù)的興趣與效率得到有效提高.

3.問題根的轉(zhuǎn)化

問題根轉(zhuǎn)化作為化歸思想解題方法之一，其通常適合數(shù)學(xué)各個階段的學(xué)習(xí)，且對數(shù)學(xué)解題具有重要的作用.該方法的運(yùn)用通常更偏重學(xué)習(xí)的后期，而后期的學(xué)習(xí)通常也是學(xué)習(xí)中最容易忽略的.比如，高中數(shù)學(xué)的后期，教師與學(xué)生通常更注重通過復(fù)習(xí)題的形式，對數(shù)學(xué)概念實施鞏固復(fù)習(xí)，以強(qiáng)化學(xué)生解題數(shù)學(xué)難題的思路，但是卻忽視了做題的本質(zhì)，致使學(xué)生在做基礎(chǔ)題時，更容易失分.而通過問題根轉(zhuǎn)化，學(xué)生在面對類似問題根的問題時，則能有效防止不當(dāng)問題的出現(xiàn)，并以現(xiàn)象直接抵制本質(zhì)，從而使學(xué)生將學(xué)習(xí)的重點放在疑難問題的解決時，還能對基礎(chǔ)知識進(jìn)行熟悉與掌握.比如，三角函數(shù)、開方、分母等相關(guān)取值范圍的問題當(dāng)中，如果忽視了其中的任何定義區(qū)間，就會解錯范圍.而如果通過問題根轉(zhuǎn)化的思維，則能有效防止類似問題的出現(xiàn).另外，在對數(shù)學(xué)函數(shù)進(jìn)行學(xué)習(xí)的時候，還需注重基本函數(shù)的轉(zhuǎn)化，將其轉(zhuǎn)化成根題后，把復(fù)雜函數(shù)進(jìn)行簡單化，這通常對復(fù)雜函數(shù)問題的解決有著重要作用.

4.函數(shù)問題轉(zhuǎn)變?yōu)閹缀螁栴}

高中數(shù)學(xué)的函數(shù)教學(xué)時，在面對難度比較大的問題時，如果通過常規(guī)的方法進(jìn)行解題，不僅計算量相對較大，而且在解題的時候，還會出現(xiàn)由于解題錯誤而造成結(jié)果錯誤的現(xiàn)象.因此，在面對類似問題的時候，就需注重化歸思想的運(yùn)用，對函數(shù)問題實施轉(zhuǎn)化，變成幾何問題，以此對解題步驟實施簡化，更直觀、形象的理解與分析相關(guān)問題，并求取出答案.比如，對函數(shù)極值問題進(jìn)行求取時，可把函數(shù)轉(zhuǎn)化為常見的函數(shù)形式實施分解計算，并對其實施拆分，或者繪圖，把極值轉(zhuǎn)化為函數(shù)區(qū)間的函數(shù)圖形的最大或最小距離，以促使學(xué)生的解題效率得到有效提高.

5.未知向已知的轉(zhuǎn)化

高中數(shù)學(xué)的函數(shù)教學(xué)時，數(shù)學(xué)教師與學(xué)生通常將學(xué)習(xí)重點放在難題解答與復(fù)習(xí)當(dāng)中，通常會忽視已經(jīng)做過的題，而通過新題實現(xiàn)自我提升，這就會使以往做的題失去其價值.比如，在傳統(tǒng)的復(fù)雜試題當(dāng)中，或者多個綜合的，將以前做過的試題當(dāng)作已知的條件，運(yùn)用于新題的解決中，通常效果更好，這就是通過已知對未知進(jìn)行解決的過程.另外，未知向已知的轉(zhuǎn)化，學(xué)生還能更好地通過數(shù)學(xué)問題的體驗產(chǎn)生新思維，從而深刻體會到數(shù)學(xué)學(xué)習(xí)的魅力.

綜上所述，高中數(shù)學(xué)的函數(shù)問題解答時，通過化歸思想的運(yùn)用，不僅能促進(jìn)函數(shù)問題的高效解答，而且還能使學(xué)生有效分析與總結(jié)相關(guān)函數(shù)問題，以深化學(xué)生對數(shù)學(xué)知識的應(yīng)用.同時，高中數(shù)學(xué)開展教學(xué)時，學(xué)生也需對化歸思想的充分領(lǐng)悟與掌握，通過解題思路與整個過程的記錄與總結(jié)，對數(shù)學(xué)函數(shù)的學(xué)習(xí)當(dāng)中的不足實施高效、細(xì)致的補(bǔ)缺補(bǔ)漏，以促使數(shù)學(xué)學(xué)習(xí)效率得到全面提高.