提高高中數學教學質量的有效策略
石 瀅
(江蘇省鹽城中學 224000)
當下高中數學教學中存在一個誤區,就是在學生思維的培養上通常對知識傳遞產生依賴性,卻不是采用專門的思維訓練方式,使得學生解決問題的能力沒有明顯提升,學生的應試能力依然是衡量學生學習質量的重要標準.這就意味著學生數學綜合素質停留在理論層面,沒有落實到具體的教學工作中.所以,教師要著力提高課堂教學質量.
一、高中數學教學中塑造翻轉課堂促進師生交互
翻轉課堂與傳統課堂的重要區別就是不按照教師講課、學生聽課的教學過程展開,而是學生自主學習,教師根據學生的知識需求展開教學.教師要注意引導學生,讓學生對課堂教學內容有深刻的印象,并留存在大腦中,對學生更好地理解數學知識起到一定的促進作用.從翻轉課堂教學形式來看,其是基于計算機技術展開的,教師將主要的教學內容制作為課件傳遞到指定的教學平臺上,學生只要能上網,就可以登陸平臺觀看課件,達到課前預習的效果.在進行課堂教學的時候,教師在講課之前用三五分鐘的時間播放課件,讓學生提出不懂之處,教師以幫助學生展開思維的方式實施指導性教學,而不是將教材內容托盤而出.當然,學生遇到難以理解的問題的時候,教師鼓勵學生利用互聯網查閱資料自行解決.互聯網是教師與學生溝通的橋梁,可以確保教師對學生的學習情況全面了解,學生也可以與教師共同探討問題,從而拉近了師生之間的距離,為提高教學質量創造條件.
比如:在直線與平面的位置關系教學中,如果設定一條直線a與一個平面之間沒有公共點,就可以明確直線a與平面之間是處于平行狀態的.可是,當直線a與平面之間只有一個公共點的時候,就可以明確直線a與平面之間是相交的;當直線a與平面之間有兩個公共點的時候,就可以證明直線是在平面之內的.
讓學生觀看課件.課件所表達的內容是直線與平面之間的各種關系,用三維立體圖象表達.直線是無限延伸的,平面也是如此.當平面與直線沒有交點的時候,必然是處于平行狀態的.教師操作課件讓學生觀看,也可以讓學生操作課件,進行各種嘗試,認識到,直面與平面平行,無論如何都不會有交點.
當學生對這個定理產生直觀印象之后,教師就可以與學生討論如何推導證明的問題.
已知:l∥α,l∥β,α∩β=m,求證:l∥m.
具體的證明過程如下:
取A∈α,由A、l確定平面γ,記γ∩α=a.由l∥α知l∥a.同理取B∈β,由B、l確定平面δ,記δ∩β=b,則l∥b.因而a∥b,則a∥β.又α∩β=m,則a∥m.但l∥a,所以l∥m.
證明完成后,教師要引導學生反思,了解判定定理的實質性內容,三個判定條件都是不可缺的.在定理的證明過程中,主要是找出與已知直線平行的直線.
二、高中數學教學中采用矛盾分析法指導學生分析問題
在高中數學教學中,教師要認識到數學知識本身就是一個矛盾體,在教學中要充分利用數學知識的這一點,引導學生用正確的方法學習數學知識并思考問題.矛盾問題屬于哲學范疇.學生在思考問題的時候利用哲學思維,繁瑣的數學邏輯就會變得清晰了.數學與哲學有關系嗎?說到這里也許很多人不理解.世界上一些著名的數學家同時也是哲學家,比如伽利略,迪卡爾等等,他們在分析數學問題的時候會運用哲學的思維方式.哲學是抽象的,其要解決的是最基本的問題,也就是說,運用哲學思維可以尋求問題的本源.比如,數學中公理是如何形成的,就要對數學發展歷史進行追溯,這其中就涉及到哲學問題.萊布尼茲是計算機二進制的發明者,他提出,如果哲學語言像數學中的符號那樣精確的時候,一切都將成為必然,不會存在模糊的中間狀態,或者是對的,或者是錯的.計算機的運行模式就是間接模擬人的思維.可見,數學家在思考問題的時候,也會運用哲學思維模式.基于此,在高中數學教學中,數學教師不妨將哲學思維合理運用,對學生進行指導教學,讓學生運用哲學邏輯解決數學問題,不僅學習效率提高了,而且對學生數學思維品質的培養非常有效.高中數學教學中,需要直接面對的問題就是教和學的問題,這就是一對矛盾體.運用哲學中矛盾論的觀點對這個問題進行分析、研究,認識到教學中存在矛盾是必然的,數學教學尤其如此.數學知識中,各個部分之間同樣存在矛盾,在各個知識環節以及每個知識點中都能夠體現出來.教學內容不同,就要采用相應的的教學方法,所獲得的數學結論也是不同的.
在教學中用矛盾分析法,用矛盾轉化的規律對數學問題予以解決.
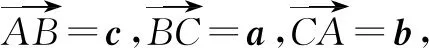
在這道題的證明中,需要觀察條件,通過對條件進行推理就可以猜想出結果,之后將特殊值選擇出來代入,進行驗證,就可以明確結論.在證明的過程中,采用矛盾分析法將條件與結論之間存在差異找出來,同時將內在聯系找出來,采用各種方法將雙方的差異消除.由此可見,矛盾分析法屬于是化歸的思想,是按照思維規律進行操作的結果.

