一個具有多翼吸引子的四維多穩態超混沌系統

鮮永菊， 扶坤榮， 徐昌彪,2

(1.重慶郵電大學 通信與信息工程學院，重慶 400065； 2.重慶郵電大學 光電工程學院，重慶 400065)

混沌是非線性系統所特有的一種現象，表現出豐富的動力學行為，在信息、生物、經濟等領域有廣泛的應用前景，近年來已成為人們研究的熱點[1-5]。

混沌系統中的多穩態是指系統在給定參數下存在兩個或多個吸引子共存，反映了系統的狀態多樣性[6-8]。混沌系統中的多翼即為吸引子具有兩個或多個翅膀，體現了系統的結構多樣性[9-11]。顯然，存在多翼吸引子的多穩態混沌系統表現出更加復雜的動力學行為，具有更為重要的理論研究意義和工程應用價值[12-15]。譬如，把這種系統應用于信息加密時，密鑰的選取可以基于多穩態下的不同吸引子，也可以基于不同參數取值下的不同吸引子或者多翼吸引子中的不同翅膀，從而使系統獲得更好的保密性能[16]。

目前，只有少量文獻報道了具有多翼吸引子的四維多穩態混沌系統。Lai等[17]通過引入Signum函數，構造了一個具有至少7種吸引子共存類型(不同運動狀態和拓撲結構的吸引子共存視為不同類型)的四維混沌系統。隨著參數的變化，四翼混沌吸引子可分解為兩個共存的雙翼混沌吸引子。Zhang等[18]提出了一個具有至少10種吸引子共存類型的四維混沌系統。隨著參數的變化，此系統可以產生從單翼到四翼的混沌吸引子。

本文構造了一個只有1個平衡點的四維超混沌系統，此系統具有至少12種吸引子共存類型。在多組參數值下，系統均存在不同類型的吸引子共存，譬如：兩個周期吸引共存，周期與擬周期吸引子共存，雙翼混沌與超混沌吸引子共存，兩個雙翼混沌吸引子共存，雙翼與四翼混沌吸引子共存，兩個雙翼超混沌吸引子共存，兩個雙翼擬周期吸引子共存，兩個雙翼超混沌、四翼混沌、四翼超混沌等四個吸引子共存。特別地，在給定參數值下，四翼超混沌吸引子可分解為兩個共存的雙翼超混沌吸引子。

1 系統模型與基本特性分析

1.1 系統模型

系統的數學模型如式(1)所示。其中，x，y，z，w為系統狀態變量，a，b，c，d為系統參數。取a=6，b=4，c=8，d=2，初始值為[1,2,3,4]時，系統存在一個典型的四翼蝶形超混沌吸引子，如圖1所示。此時系統的四個Lyapunov指數(LE)為1.657，0.117，0，-37.324。顯然，系統有兩個正的Lyapunov指數，表明其為一個超混沌系統。Lyapunov維數DL=3+(LE1+LE2+LE3)/|LE4|=3.048，即為分數維，從而驗證了系統是分形的。

(a) x-y

(b) x-z

(c) x-w

(d) y-z

(1)

1.2 平衡點及其穩定性

令非線性方程(1)的左邊等于0，即

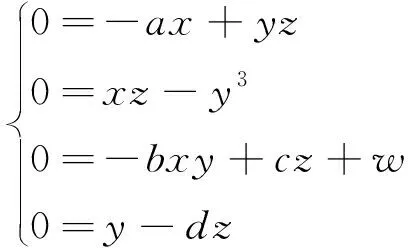
(2)

求解方程可得唯一平衡點，即S0=(0,0,0,0)。在平衡點處線性化系統，得其Jacobi矩陣為

(3)

令det(λI-J)=0，得到多項式

f(λ)=λ4+(a-c)λ3+(-ac+d)λ2+adλ

(4)

1.3 時域波形圖和Poincaré截面

取a=6，b=4，c=8，d=2，初始值為[1,2,3,4]時，采用四階龍格-庫塔算法對式(1)進行求解，可得x的時序圖，如圖2所示。顯然，系統作非周期運動。z=0上的Poincaré截面如圖3所示。可以看出，Poincaré截面上形成了具有分形結構的密集點，表明了圖1所示的四翼超混沌吸引子的存在。

圖2 狀態變量x的時序圖

圖3 z=0上系統的Poincaré截面

1.4 Lyapunov指數

取b=4，c=8，d=2，初始值為[1,2,3,4]時，Lyapunov指數和x隨a變化的分岔圖分別如圖4(a)和圖5(a)所示?？芍琣由0增加到10時，系統運動狀態變化過程為：周期→擬周期→混沌→超混沌→混沌。

取a=6，c=8，d=2，初始值為[1,2,3,4]時，Lyapunov指數和x隨b變化的分岔圖分別如圖4(b)和圖5(b)所示。可知，b由0增加到20時，系統運動狀態變化過程為：混沌→超混沌→混沌→擬周期→周期。

取a=6，b=4，d=2，初始值為[1,2,3,4]時，Lyapunov指數和y隨c變化的分岔圖分別如圖4(c)和圖5(c)所示?？芍琧由0增加到30時，系統運動狀態變化過程為：周期→擬周期→混沌→超混沌→混沌。

(a) 參數a變化

(b) 參數b變化

(c) 參數c變化

(d) 參數d變化

(a) 參數a變化

(b) 參數b變化

(c) 參數c變化

(d) 參數d變化

取a=6，b=4，c=8，初始值為[1,2,3,4]時，Lyapunov指數和x隨d變化的分岔圖分別如圖4(d)和圖5(d)所示。可知，d由0增加到30時，系統運動狀態變化過程為：混沌→超混沌→混沌。

2 多穩態特性和多翼拓撲結構

2.1 多穩態特性

情形1：參數a變化

取a∈[0,5]，b=4，c=8，d=2，初始值為[1,±2,3,4]時，x隨a變化的分岔圖如圖6(a)所示?？芍?，隨著a的變化，系統存在多種類型的吸引子共存：當a=2時，兩個周期吸引子共存；當a=2.9時，擬周期和周期吸引子共存；當a=3.2時，兩個混沌吸引子共存。Lyapunov指數如表1所示，x-y平面相圖如圖7(a)～圖7(c)所示，表明當a∈[0,5]時系統的多穩態特性由x來體現。

(a) a∈[0,5]

(b) a∈[8.8,10]

(a) a=2

(b) a=2.9

(c) a=3.2

(e) a=8.9

取a∈[8.8,10]，b=4，c=8，d=2，初始值為[1,2,±3,4]時，z隨a變化的分岔圖如圖6(b)所示?？芍?，隨著a的變化，系統存在多種類型的吸引子共存：當a=10時，兩個雙翼混沌吸引子共存；當a=8.9時，雙翼混沌和四翼混沌吸引子共存。Lyapunov指數如表1所示，共存吸引子如圖7(d)～圖7(e)所示，表明當a∈[8.8,10]時系統的多穩態特性由z來體現。

情形2：參數b變化

取b∈[9,18]，a=6，c=8，d=2，初始值為[±1,2,3,4]時，x隨b變化的分岔圖如圖8(a)所示。可知，隨著b的變化，系統存在多種類型的吸引子共存：當b=9.9時，兩個超混沌吸引子共存；當b=14時，兩個擬周期吸引子共存；當b=18時，兩個周期吸引子共存。Lyapunov指數如表1所示，x-y平面相圖如圖8(b)～圖8(d)所示，表明當b∈[9,18]時系統的多穩態特性由x來體現。

(a) 分岔圖

(b) b=9.9的共存吸引子

(c) b=14的共存吸引子

(d) b=18的共存吸引子

情形3：參數c變化

取c∈[0,4]，a=6，b=4，d=2，初始值為[1,±2,3,4]時，y隨c變化的分岔圖如圖9(a)所示?？芍?，隨著c的變化，系統存在多種類型的吸引子共存：當c=0.4時，兩個周期吸引子共存；當c=1.25時，兩個擬周期吸引子共存；當c=2時，兩個混沌吸引子共存。Lyapunov指數如表1所示，y-z平面相圖如圖9(b)～圖9(d)所示，表明當c∈[0,4]時系統的多穩態特性由y來體現。

情形4：參數a=6，b=4，d=2，c=21

取a=6，b=4，c=21，d=2，初始值為[±1,2,3,4]、[1,-2,3,4]和[-1,2,-3,4]，有2個孤立的雙翼超混沌吸引子、1個四翼蝶形超混沌吸引子和1個四翼蝶形混沌吸引子共存。Lyapunov指數如表1所示，相圖和時序圖分別如圖10(a)～圖10(c)所示，表明了共存吸引子的存在，且系統的多穩態特性由x來體現。

(a) 分岔圖

(b) c=0.4的共存吸引子

(c) c=1.25的共存吸引子

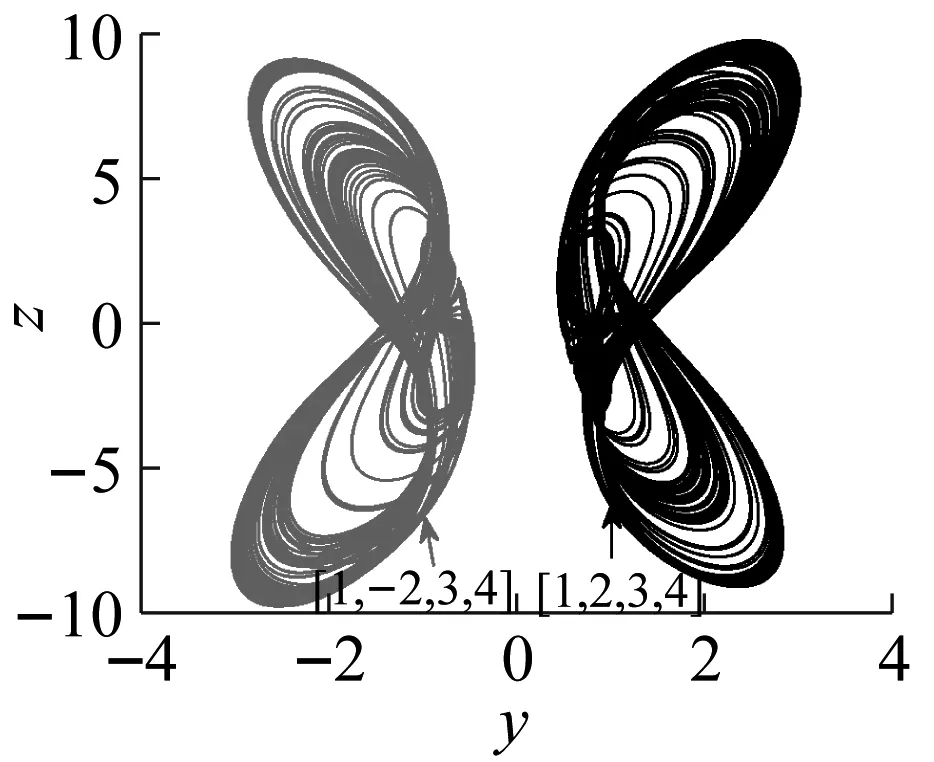
(d) c=2的共存吸引子

(a) [1,2,3,4]和[-1,2,-3,4]

(b) [-1,2,3,4]

(c) [1,-2,3,4]

2.2 多翼拓撲結構

情形1：相同參數取值，不同初始值下的多翼變化

如圖10(a)～圖10(c)所示，在同一組參數取值下，取不同的初始值時，系統的四翼蝶形超混沌吸引子可以分解為兩個孤立的雙翼超混沌吸引子，也可以演變為一個四翼蝶形混沌吸引子。

表1 不同參數和初始值下的共存吸引子

情形2：相同初始值，不同參數取值下的多翼變化

初始值取[1,2,3,4]，固定a=6，c=8，d=2，b的取值由10.1→8→6→1.45時，系統行為的演變過程為：雙翼混沌吸引子→雙翼超混沌吸引子→四翼蝶形超混沌吸引子→四翼蝶形混沌吸引子。相圖如圖11(a)～圖11(d)所示，Lyapunov指數如表2所示?？芍?，在初始值相同時，取不同的參數值，系統出現處于不同運動狀態的雙翼吸引子和四翼蝶形吸引子。

(a) b=10.1 (b) b=8 (c) b=6 (d) b=1.45

表2 不同參數下的吸引子拓撲結構

3 系統的電路仿真

3.1 模擬電路仿真

利用Multisim電路仿真軟件，采用線性電阻、電容、LM2924N運算放大器、AD633模擬乘法器，實現混沌系統的電路設計與模擬。根據系統的動力學方程，設計電路原理圖如圖12所示，其中乘法器的輸出增益為0.1。改變不同電容和電阻的值，以實現耗散超混沌系統電路的模擬。根據電路原理圖以及電路理論，得自激振蕩電路方程如式(5)所示。其中R1～R15為線性電阻，C1～C4為電容。取電容C1=C2=C3=C4=1 μF，電阻R7=R8=R11=R12=R14=R15=1 kΩ。

(5)

當a=6，b=4，c=8，d=2時，對比式(1)和式(5)，可以得到電阻值如式(6)。根據初始值[1,2,3,4]，可得Vx=1，Vy=2，Vz=3，Vw=4。仿真結果如圖13所示，表明模擬電路仿真結果與數值仿真結果一致。

(6)

圖12 電路原理圖

(a) x-y

(b) x-z

(c) x-w

(d) y-z

3.2 數字電路仿真

由于模擬器件的性能容易受到環境溫度、濕度以及器件老化的影響，故模擬電路實現混沌系統會嚴重影響系統的動力學特性，限制了模擬混沌電路在工程中的應用。采用FPGA數字電路技術實現混沌系統可以很好地避免這些問題，保證了混沌吸引子的穩定可靠。由于系統是一個連續時間系統，FPGA無法直接處理，本文采用Euler算法將系統(1)離散化，得到的差分方程為

(7)

式中:a=6，b=4，c=8，d=2;迭代步長Δt=0.001。

Xilinx RTL原理圖如圖14所示，FPGA硬件及其實驗效果如圖15所示。當初始值為[1,2,3,4]時，由示波器隨機捕獲的系統相位圖如圖16所示?？芍?，數字電路仿真結果與模擬電路仿真以及數值仿真結果一致。

圖14 Xilinx RTL原理圖

圖15 FPGA硬件及其實驗效果

(a) x-y

(b) x-z

(c) x-w

(d) y-z

4 系統復雜度分析及超混沌序列的隨機性測試

4.1 系統復雜度分析

復雜度測度是描述混沌系統復雜行為的一種重要方法。混沌系統的復雜度是指采用相關算法衡量混沌序列接近隨機序列的程度。復雜度值越大，序列越接近隨機序列[19]。

混沌序列的復雜度分為行為復雜度和結構復雜度，前者測量短時間窗口內序列產生新模式的概率大小，后者通過變換域內的頻率特性和能量譜特性來分析序列的復雜程度。與行為復雜性相比，結構復雜性具有全局統計意義，因為其針對的是序列的全部而不是局部。目前評價結構復雜度的算法主要有譜熵(SE)算法和C0算法。

以a和b為變量，初始值為[1,2,3,4]時系統隨參數變化的譜熵(SE)復雜度和C0復雜度分別如圖17和圖18所示。

(a) 參數a

(b) 參數b

(1) 參數a變化，b=4，c=8，d=2時，系統運動狀態從周期變到擬周期，SE和C0較??；從擬周期向混沌、超混沌狀態轉變時，SE和C0逐漸增加到最高值；維持超混沌狀態時，SE和C0在最高值附近波動；最終系統處于混沌狀態時，SE和C0減小至較高值。

(a) 參數a

(b) 參數b

(2) 參數b變化，a=6，c=8，d=2時，系統運動狀態從混沌變到超混沌狀態時，SE和C0由較高值上升到最高值；從超混沌變到混沌狀態時，SE和C0逐漸減小至較高值；從混沌逐漸變到擬周期、周期狀態時，SE和C0進一步減小，最終維持在一個較低值。

4.2 超混沌序列的隨機性測試

取a=6，b=4，c=8，d=2，初始值為[1,2,3,4]時，采用四階龍格-庫塔法求解系統得到超混沌序列。利用美國國家標準技術研究所(NIST)的SP800-22 Revla的15種測試方法[20]檢驗此超混沌序列的隨機特性(P-value≥0.01表示測試的比特序列是隨機的，否則認為序列是非隨機的)，測試結果如表3所示。可知，超混沌序列通過了15項隨機測試。

表3 基于SP800-22 Revla的15項測試結果

5 結 論

本文構建了一個新型的四維超混沌系統，數值分析了系統的基本動力學特性，仿真了系統的模擬電路和數字電路，探討了系統的動態復雜度，測試了系統超混沌序列的隨機性，得出如結論：

(1) 系統只有一個平衡點，且為不穩定平衡點。

(2) 系統表現出豐富的多穩態特性，即在多組參數值下，系統均存在不同類型的吸引子共存，譬如：兩個周期吸引共存，周期與擬周期吸引子共存，雙翼混沌與超混沌吸引子共存，兩個雙翼混沌吸引子共存，雙翼與四翼混沌吸引子共存，兩個雙翼超混沌吸引子共存，兩個雙翼擬周期吸引子共存，兩個雙翼超混沌、四翼混沌、四翼超混沌等四個吸引子共存。

(3) 在給定參數值下，四翼超混沌吸引子可分解為兩個共存的雙翼超混沌吸引子。

(4) 數字電路和模擬電路的仿真結果均與數值分析結果一致，表明了系統的可實現性。

(5) 在混沌和超混沌狀態下系統復雜度高，且超混沌序列通過了SP800-22 Revla的15項隨機測試。