橫向常磁場(chǎng)中鐵磁圓板的主共振特性與靜載效應(yīng)
馬冰冰, 胡宇達(dá)
(1.燕山大學(xué) 建筑工程與力學(xué)學(xué)院,河北 秦皇島 066004;2.燕山大學(xué) 河北省重型裝備與大型結(jié)構(gòu)力學(xué)可靠性重點(diǎn)實(shí)驗(yàn)室,河北 秦皇島 066004)
電磁場(chǎng)環(huán)境中圓型板及其組合結(jié)構(gòu)在工程實(shí)際中得到廣泛應(yīng)用,如:電機(jī)定子和轉(zhuǎn)子的鐵芯、電磁傳感器結(jié)構(gòu)件等,這些結(jié)構(gòu)在電磁場(chǎng)中的耦合振動(dòng)問(wèn)題是決定機(jī)電系統(tǒng)安全運(yùn)行的主要因素,因此,研究磁場(chǎng)中鐵磁圓板的非線性振動(dòng)問(wèn)題既有理論意義,也可為工程實(shí)際中機(jī)電系統(tǒng)的動(dòng)力學(xué)控制提供技術(shù)支持。并且在常磁場(chǎng)中,鐵磁圓板結(jié)構(gòu)受到靜載荷作用,從而具有初撓度,對(duì)圓板非線性振動(dòng)產(chǎn)生一定影響。
板的非線性共振問(wèn)題已得到很多學(xué)者的關(guān)注。在20世紀(jì)90年代,Okajima等[1]對(duì)懸臂矩形板的共振頻率與曲率和厚度變化的關(guān)系進(jìn)行了研究。Oh等[2]對(duì)兩種不同鋪設(shè)角度懸臂復(fù)合板的非線性組合共振問(wèn)題進(jìn)行了實(shí)驗(yàn)研究,發(fā)現(xiàn)兩種板的最大頻率差為6%。近年來(lái),Du等[3]對(duì)均勻載荷作用下阻尼夾層圓板的非線性超諧共振進(jìn)行了研究,分析了解的穩(wěn)定性和奇異性。高原文等[4]分析了在周期時(shí)變磁場(chǎng)中簡(jiǎn)支鐵磁梁式板的非線性磁彈性動(dòng)力特性與混沌現(xiàn)象。Xue等[5]研究了電磁彈性薄板的非線性無(wú)阻尼強(qiáng)迫振動(dòng),并分析了不同參量對(duì)主共振間隔、彈簧剛度特性和振幅跳躍現(xiàn)象的影響。胡宇達(dá)等[6-9]在矩形板方面,研究了四邊簡(jiǎn)支功能梯度板的主共振,磁場(chǎng)環(huán)境中導(dǎo)電薄板的亞諧共振問(wèn)題;在圓板方面,研究了磁場(chǎng)中旋轉(zhuǎn)導(dǎo)電圓板的主共振與分岔問(wèn)題以及超諧-組合共振問(wèn)題。Chen等[10]研究了不同尺寸夾層板的固有頻率,并討論了其內(nèi)共振特性。
近20年來(lái),研究者們?cè)絹?lái)越關(guān)注靜載荷下板結(jié)構(gòu)的振動(dòng)與屈曲問(wèn)題。Yamaki等[11]同時(shí)考慮了初始撓度和初始邊緣位移的影響,對(duì)均布橫向載荷作用下夾層圓板的軸對(duì)稱非線性振動(dòng)進(jìn)行了理論分析。Wang等[12]給出了靜載荷下圓板的微分方程,得到了初撓度圓板非線性振動(dòng)的周期解,并討論了初始撓度對(duì)柔性板動(dòng)力特性的影響。Du等[13]研究了均布荷載和周邊荷載作用下夾層圓板的非線性振動(dòng),并用改進(jìn)的迭代法求解振幅-頻率-載荷特性關(guān)系,分析了兩種載荷對(duì)夾層圓板振動(dòng)特性的影響。同時(shí),有些學(xué)者考慮了多場(chǎng)耦合的影響。王永崗等[14]研究了靜態(tài)溫度場(chǎng)中具有初撓度的雙層金屬薄板在周期時(shí)變橫向載荷作用下的混沌運(yùn)動(dòng)。Hu等[15-16]研究了在靜磁場(chǎng)作用下導(dǎo)電旋轉(zhuǎn)圓板的非線性自由振動(dòng)和主共振問(wèn)題,分析了頻率和振幅與靜載、磁感應(yīng)強(qiáng)度、轉(zhuǎn)速等參數(shù)之間的關(guān)系。徐學(xué)平等[17]分析了偏心轉(zhuǎn)子不計(jì)靜載荷時(shí)和考慮靜載荷時(shí)對(duì)轉(zhuǎn)子系統(tǒng)振動(dòng)特性的影響。另外,有一些學(xué)者對(duì)靜載荷作用下板的屈曲問(wèn)題進(jìn)行了研究。王德禹[18]分析了受面內(nèi)靜載荷作用的矩形板在沖擊載荷作用下產(chǎn)生的沖擊屈曲,分析了靜載荷、沖擊載荷速度及初始撓度對(duì)板的屈曲特性的影響。Babich等[19]研究了預(yù)應(yīng)力半空間板在靜載作用下的初應(yīng)力對(duì)彎矩的影響。
處于橫向常磁場(chǎng)中鐵磁圓板受到的磁體力為靜載荷,靜載荷下圓板產(chǎn)生的初撓度對(duì)系統(tǒng)振動(dòng)產(chǎn)生影響。本文研究常磁場(chǎng)中鐵磁圓板的主共振問(wèn)題,得到圓板初撓度和擾動(dòng)微分方程,利用多尺度法求解得出穩(wěn)態(tài)運(yùn)動(dòng)下的幅頻響應(yīng)方程,并通過(guò)算例分析不同電磁參量對(duì)共振振幅的影響。
1 圓板磁彈性振動(dòng)方程
1.1 圓板動(dòng)能和勢(shì)能
考慮處于外加法向磁場(chǎng)(Hn1為上表面磁場(chǎng)、Hn2為下表面磁場(chǎng))中的各向同性鐵磁圓板,在周邊夾支的邊界條件下,受到橫向載荷Pz的作用。如圖1所示,在圓板上建立柱坐標(biāo)系(r,θ,z)。其中,r、θ、z分別為徑向、環(huán)向、法向坐標(biāo);圓板厚度為h;半徑為R;質(zhì)量密度為ρ。
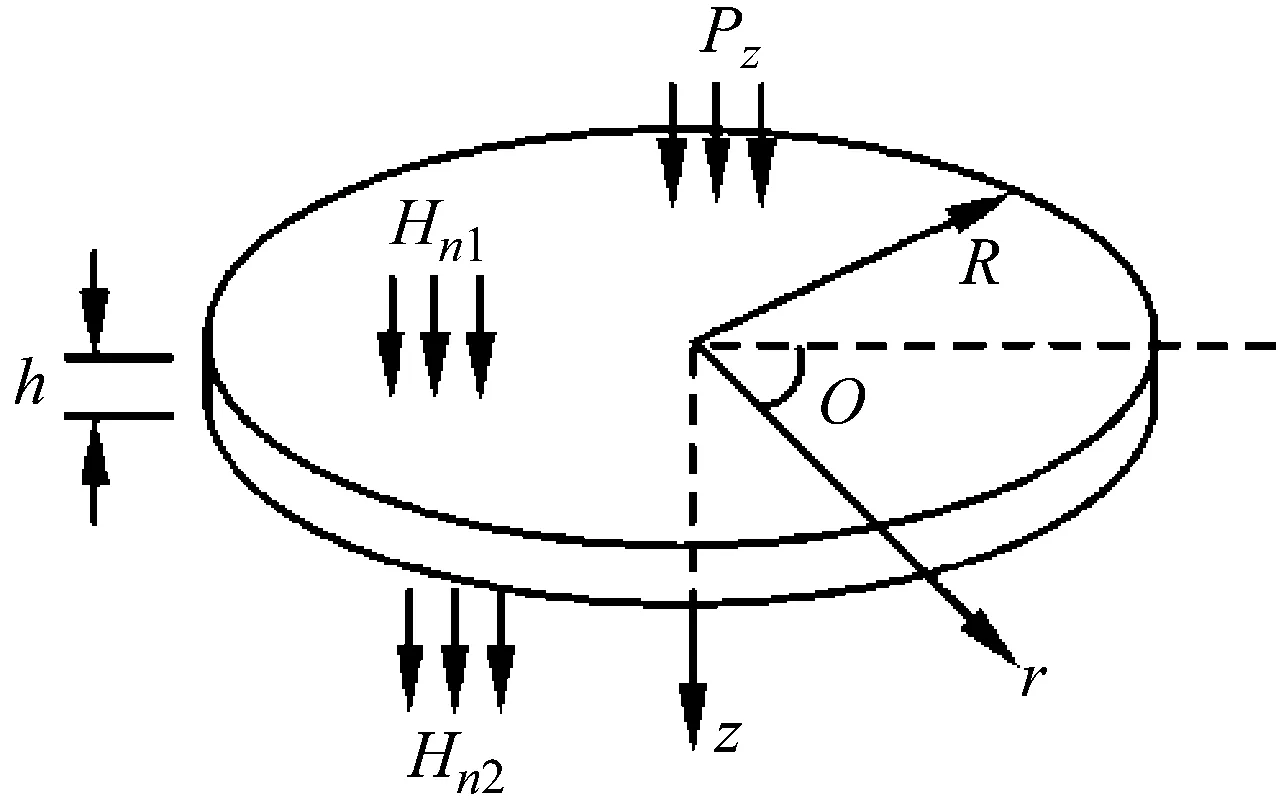
圖1 磁場(chǎng)中鐵磁圓板的力學(xué)模型
忽略面內(nèi)位移情況下,設(shè)磁場(chǎng)中鐵磁圓板板內(nèi)任意一點(diǎn)的變形位移分量的表達(dá)式為
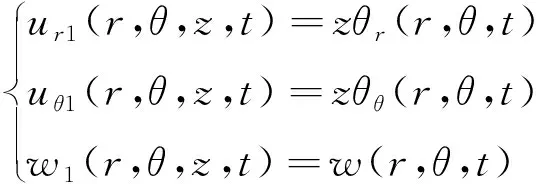
(1)
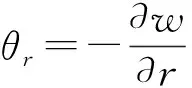
系統(tǒng)動(dòng)能表達(dá)式
(2)
圓板彎曲形變勢(shì)能表達(dá)式
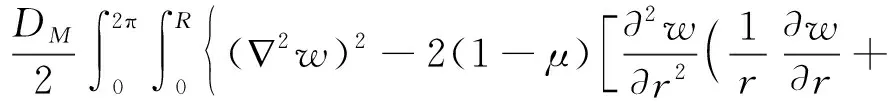
(3)
圓板中面應(yīng)變勢(shì)能表達(dá)式
(4)
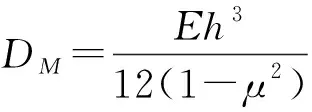
1.2 電磁力
根據(jù)磁彈性相互作用的理論模型[20],得到磁場(chǎng)中鐵磁圓板受到的磁體力
式中:Hn為圓板表面法線方向磁場(chǎng)強(qiáng)度;μ0為真空中的磁導(dǎo)率;μr為相對(duì)磁導(dǎo)率;χm為材料的磁化率,χm=μr-1。
運(yùn)動(dòng)圓板內(nèi)部產(chǎn)生渦電流效應(yīng),依據(jù)電磁理論,運(yùn)動(dòng)物體所受洛倫茲力表達(dá)式為
f(fr,fθ,fz)=J×B
(6)
式中:J為忽略電場(chǎng)強(qiáng)度時(shí)的電流密度矢量,J=σ0(V×B);B為磁感應(yīng)強(qiáng)度矢量,B=μ0μrH;σ0為電導(dǎo)率。
對(duì)式(6)沿板厚方向積分,可得電磁力矩為
(7)
(8)
橫向磁場(chǎng)中,鐵磁圓板受到的電磁力所做虛功表達(dá)式為
(9)
1.3 磁彈性振動(dòng)方程
運(yùn)用哈密頓變分原理得到
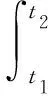
(10)
式中,δUP為橫向激勵(lì)力Pz所做虛功。
將式(2)~(4)、(9)代入式(10)中,且只考慮橫向位移情況時(shí),推得鐵磁圓板的橫向磁彈性振動(dòng)方程為
(11)
式中,Nr、Nθ、Nrθ為中面內(nèi)力。
2 靜載荷作用下圓板擾動(dòng)微分方程
當(dāng)鐵磁圓板處于常磁場(chǎng)中時(shí),即當(dāng)Hn1和Hn2為恒定值時(shí),由式(5)可得受到的磁體力為靜載荷,即:
Fz=Q
(12)
并考慮軸對(duì)稱情況,橫向磁場(chǎng)中鐵磁圓板的非線性振動(dòng)方程可寫(xiě)為
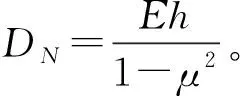
設(shè)圓板在靜載荷下產(chǎn)生微小靜撓度w0,強(qiáng)迫振動(dòng)撓度w1,總撓度為
w=w0+w1
則式(13)可以改寫(xiě)為
初始撓度滿足
(15)
設(shè)滿足周邊夾支邊界條件的位移函數(shù)為
(16)
對(duì)式(15)進(jìn)行伽遼金積分并化簡(jiǎn)得到初撓度方程
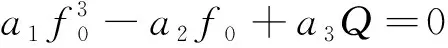
(17)
其中,
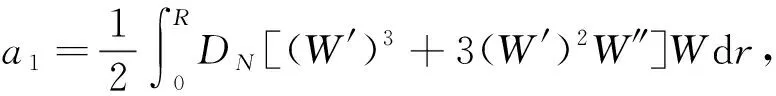
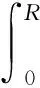
求解得到:
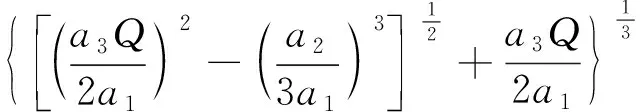
(18)
設(shè)位移函數(shù)為
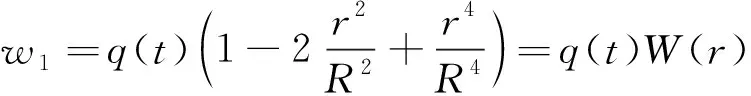
(19)
將式(15)代入到式(14)中,并進(jìn)行伽遼金積分,得到擾動(dòng)微分方程
B1q″+B2q′+B3q+B4q2+B5q3=B6Pz
(20)
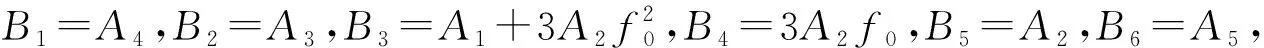
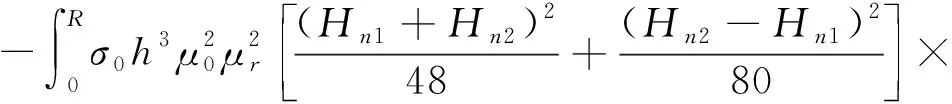
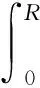
3 多尺度法求解主共振問(wèn)題
設(shè)激勵(lì)力為Pz=P0cos(ωt),對(duì)式(20)進(jìn)行量綱歸一化處理,考慮系統(tǒng)的弱非線性問(wèn)題,引入小參數(shù)ε,得到
(21)
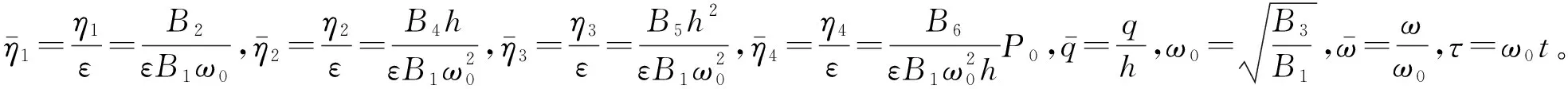
接下來(lái)應(yīng)用多尺度法對(duì)具有初撓度擾動(dòng)的系統(tǒng)主共振問(wèn)題進(jìn)行求解,分別考慮一階近似求解和二階近似求解兩種情況。
3.1 一階近似
取一階近似解
(22)
其中,T0=τ,T1=ετ。
將式(22)代入式(21)中,令的ε0、ε1項(xiàng)系數(shù)相等,可得:
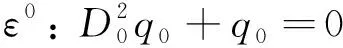
(23)
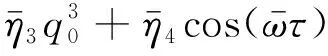
(24)
式(23)的通解為
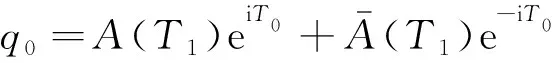
(25)
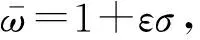
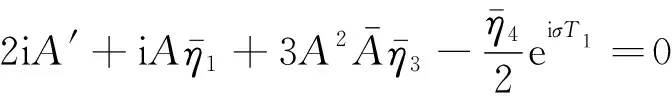
(26)
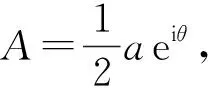
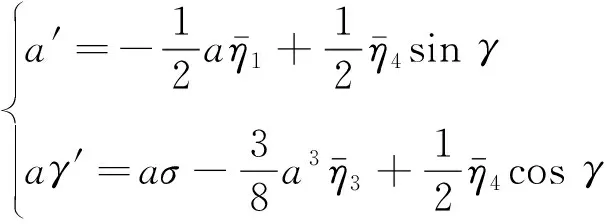
(27)
令a′=γ′=0,得到穩(wěn)態(tài)運(yùn)動(dòng)下常磁場(chǎng)中鐵磁圓板主共振幅頻響應(yīng)方程
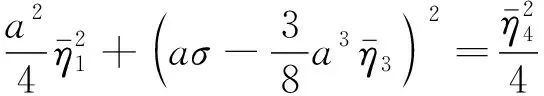
(28)
3.2 二階近似
取二階近似解
ε2q2(T0,T1,T2)
(29)
其中,T0=τ,T1=ετ,T2=ε2τ。
將式(29)代入式(21)中,并分別令ε的零次、一次、二次項(xiàng)系數(shù)相等,可得各階近似線性偏微分方程組
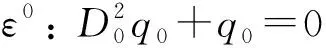
(30)
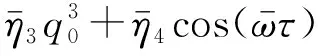
(31)
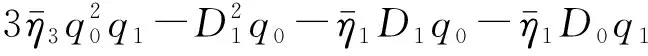
(32)
式(30)的通解為
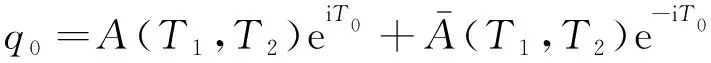
(33)
代入式(31)
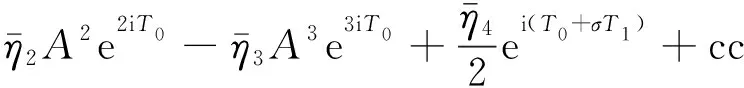
(34)
式中,cc為各等式右側(cè)各項(xiàng)共軛復(fù)數(shù)項(xiàng)之和。
消除久期項(xiàng)可得
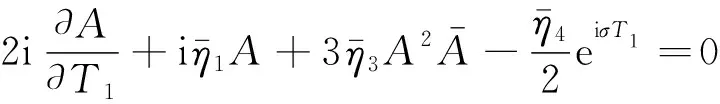
(35)
式(35)代入式(34),求解可得式(34)的特解為
(36)
將q0,q1代入式(32)中,并消除久期項(xiàng)
(37)
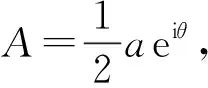
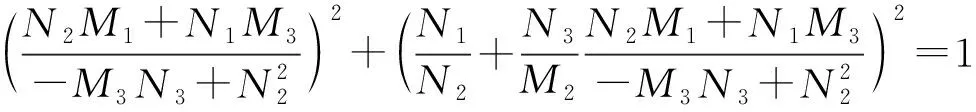
(38)
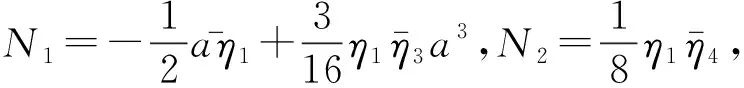
4 數(shù)值分析
針對(duì)橫向交變磁場(chǎng)中受到橫向簡(jiǎn)諧激勵(lì)力作用的軟鐵磁馬氏體鋼制圓薄板進(jìn)行數(shù)值分析。尺寸參數(shù)為:R=0.3 m,h=0.005 m(圖2(a)和圖3(a)除外),物理參數(shù)取值如表1。

表1 圓薄板物理參數(shù)[21]
圖2和圖3分別繪制了一階近似和二階近似求解方法下鐵磁圓板的幅頻特性曲線圖。曲線表明,振幅在共振區(qū)域(εσ≈0附近)顯著增加,曲線存在向右偏移現(xiàn)象,呈現(xiàn)硬彈簧特性。且隨著調(diào)諧值由負(fù)數(shù)逐漸增加為正數(shù)時(shí),共振幅值由單值解變?yōu)槎嘀到狻S蓤D2(a)和圖3(a)可看出,隨著板厚增加,共振區(qū)域逐漸變窄,且當(dāng)下表面磁場(chǎng)強(qiáng)度為100 A/m時(shí),一階近似與二階近似解得的振幅十分相近,但圖3(a)中的曲線振幅稍大。由圖2(b)和圖3(b)可看出,磁場(chǎng)強(qiáng)度較小時(shí)圖2(b)中的曲線沒(méi)有變化,而圖3(b)中曲線隨著磁場(chǎng)強(qiáng)度增大,曲線向右偏移的角度變小,有向左偏移的趨勢(shì)。出現(xiàn)這種現(xiàn)象的原因可見(jiàn)式(28)和式(38),二次非線性項(xiàng)系數(shù)中含有靜載荷項(xiàng),利用一階近似多尺度法求解時(shí),幅頻響應(yīng)方程中不體現(xiàn)二次項(xiàng),常磁場(chǎng)僅影響阻尼項(xiàng)和固有頻率,因此磁場(chǎng)較小時(shí)共振曲線無(wú)變化;而二階近似求解時(shí),隨著磁場(chǎng)強(qiáng)度增加,二次項(xiàng)系數(shù)增大,其非線性增大,因此曲線逐漸向左偏移。圖2(c)和圖3(c)中曲線表明,隨著激勵(lì)力幅值增大,共振區(qū)域逐漸拓寬,上支曲線和下支下半部分振幅增大,下支上半部分曲線振幅減小。
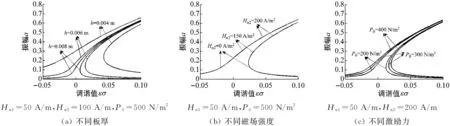
圖2 一階近似幅頻特性曲線圖
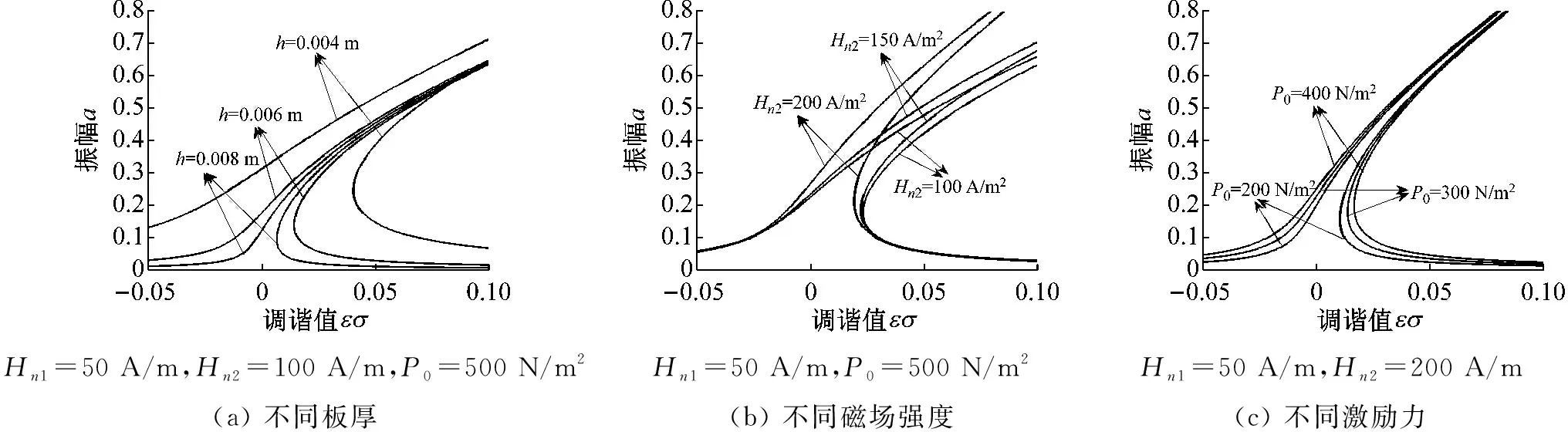
圖3 二階近似幅頻特性曲線圖
圖4和圖5分別繪制了一階近似和二階近似求解下的振幅-磁場(chǎng)強(qiáng)度特性曲線圖。由各圖中的曲線可以看出,振幅-磁場(chǎng)強(qiáng)度特性曲線關(guān)于磁場(chǎng)強(qiáng)度Hn2=0 A/m呈左右對(duì)稱形式,且在磁場(chǎng)強(qiáng)度較小時(shí)便激發(fā)了共振,振幅較大。由圖4看出,當(dāng)調(diào)諧值較小或激勵(lì)力幅值較大時(shí),曲線為單值解;隨著調(diào)諧值增加或激勵(lì)力幅值減小,兩腰側(cè)曲線開(kāi)始內(nèi)縮,存在多值解,直至最后分離形成上部分封閉曲線。圖5曲線呈牛角狀,當(dāng)調(diào)諧值較小、激勵(lì)力幅值較大時(shí)曲線兩腰向內(nèi)微收,隨著調(diào)諧值增加、激勵(lì)力幅值減小,兩腰側(cè)曲線內(nèi)縮更加明顯,最后兩部分曲線分離形成上部分封閉曲線,存在3個(gè)解。
通過(guò)對(duì)比圖4和圖5發(fā)現(xiàn),當(dāng)磁場(chǎng)強(qiáng)度較小時(shí)一階與二階近似共振振幅大小相近,而當(dāng)磁場(chǎng)強(qiáng)度增加到250 A/m時(shí),二階近似振幅急劇減小,但由于一階近似求解時(shí)不體現(xiàn)含有常磁場(chǎng)靜載的二次非線性項(xiàng),因此一階近似振幅在Hn2=12 000 A/m左右時(shí)才急劇減小。綜上所述,磁場(chǎng)強(qiáng)度較小時(shí)一階近似與二階近似計(jì)算結(jié)果相近,而磁場(chǎng)強(qiáng)度較大時(shí),二階近似計(jì)算結(jié)果更加準(zhǔn)確。
圖6和圖7給出的是不同調(diào)諧值與不同磁場(chǎng)強(qiáng)度下一階近似和二階近似振幅-激勵(lì)力幅值特性曲線圖。
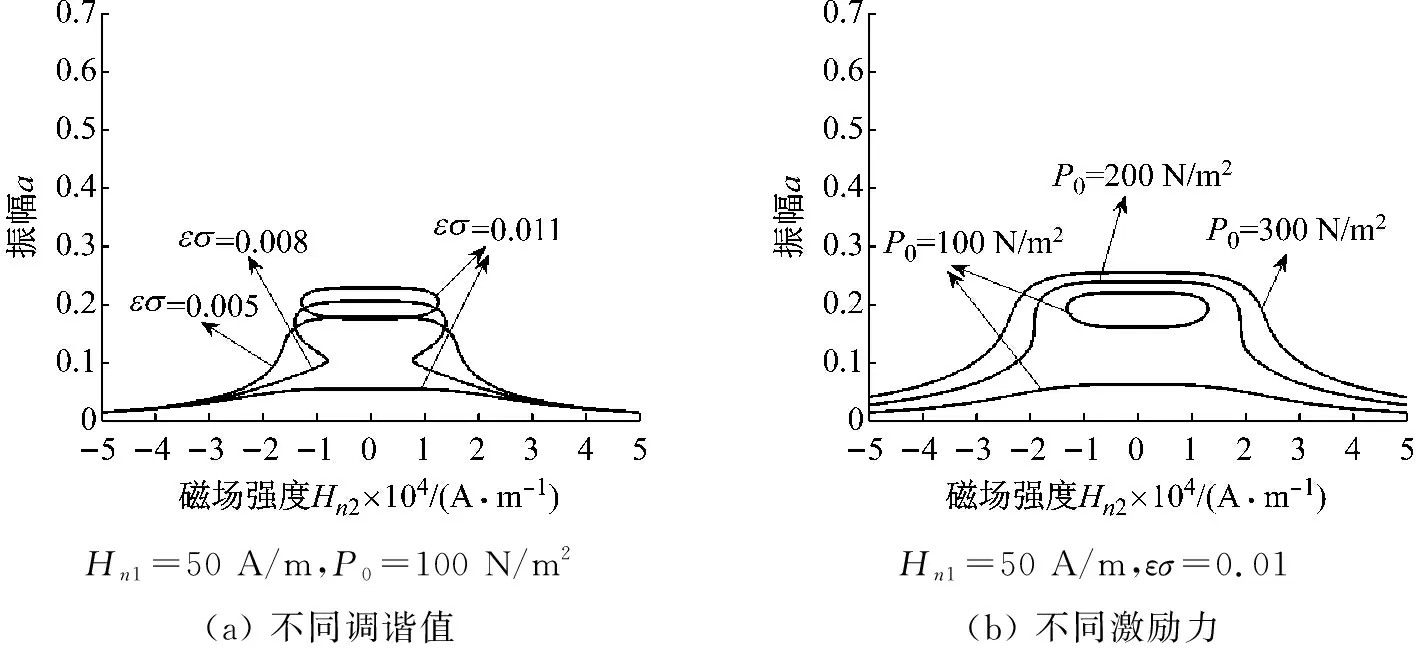
圖4 一階近似振幅-磁場(chǎng)強(qiáng)度特性曲線圖
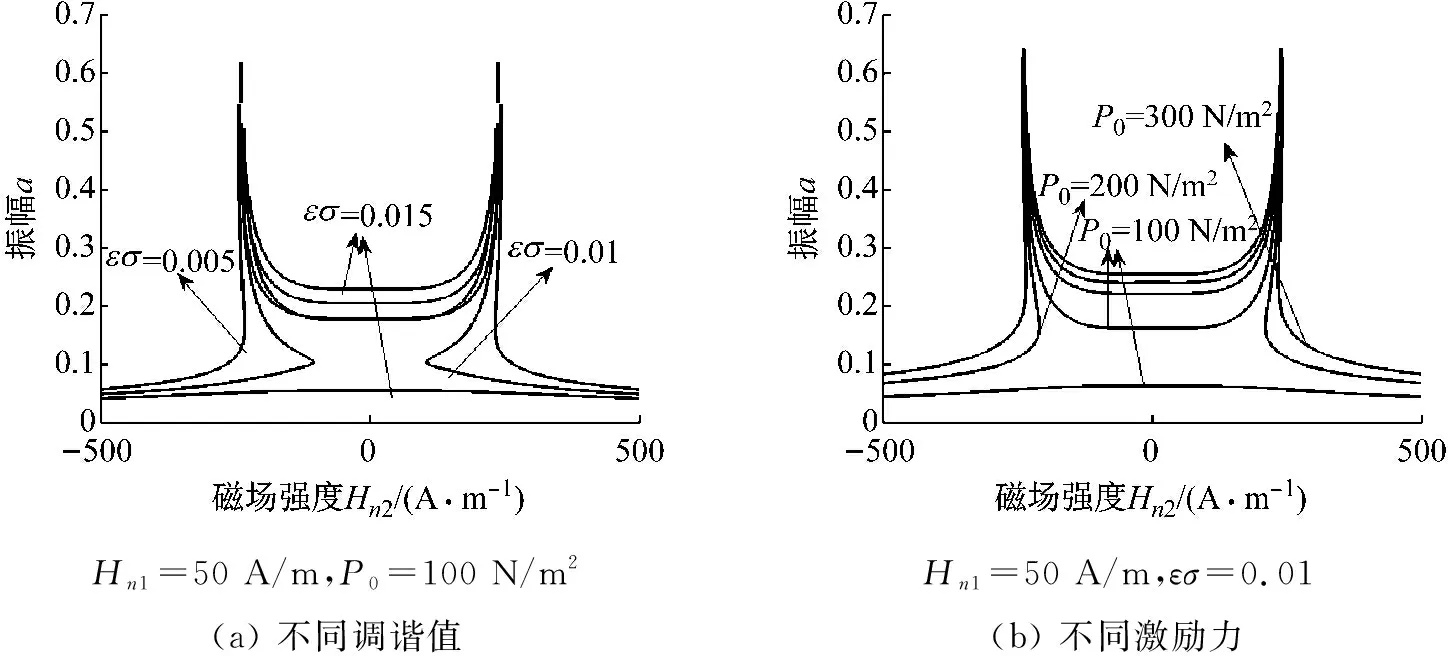
圖5 二階近似振幅-磁場(chǎng)強(qiáng)度特性曲線圖
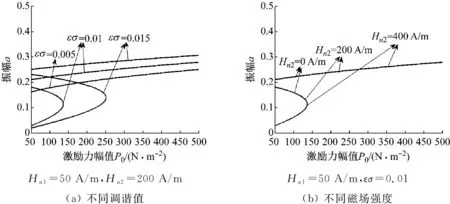
圖6 一階近似振幅-激勵(lì)力幅值特性曲線圖
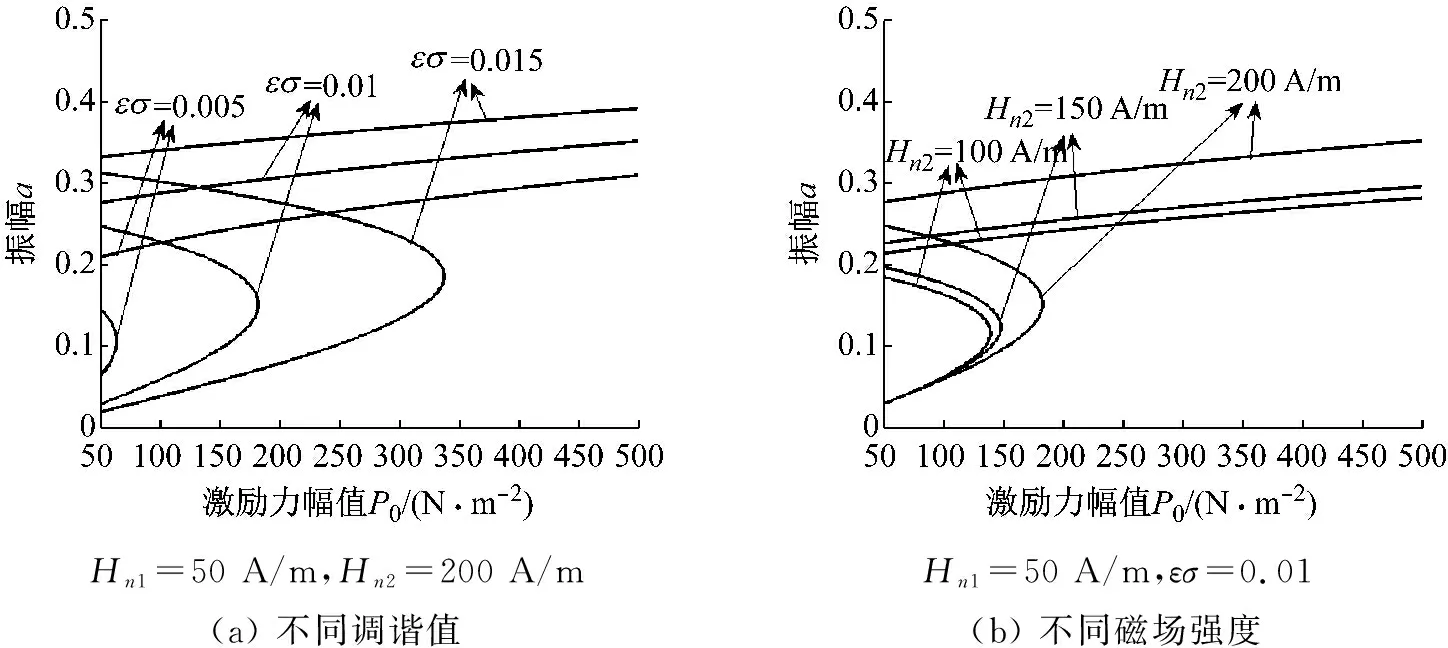
圖7 二階近似振幅-激勵(lì)力幅值特性曲線圖
圖中曲線表明,當(dāng)激勵(lì)力幅值較小時(shí)便可以激發(fā)系統(tǒng)的主共振現(xiàn)象,且出現(xiàn)多值解,之后振幅隨著激勵(lì)力幅值的增大由多值解變?yōu)閱沃到猓覇沃到饩徛黾印G€向左偏移,呈現(xiàn)軟彈簧特性。
比較圖6(a)和圖7(a)看出,在Hn2=200 A/m時(shí),圖7(a)共振幅值大于圖6(a)的共振幅值,隨著調(diào)諧參數(shù)增大,上支曲線與下支上半部分曲線共振振幅增大,而下支下半部分曲線振幅減小。由圖6(b)和圖7(b)相比較可看出,圖6(b)中在磁場(chǎng)強(qiáng)度數(shù)值較小時(shí),曲線沒(méi)有變化;圖7(b)中上支曲線與下支上半部分曲線共振振幅隨著磁場(chǎng)強(qiáng)度的增加而增加。
圖8和圖9通過(guò)提取共振曲線出現(xiàn)多值解的臨界點(diǎn)繪制了分岔點(diǎn)變化圖。其中:圖8(a)和圖9(a)分別提取了圖2(a)和圖3(a)中的多值解臨界點(diǎn),繪制出板厚-調(diào)諧參數(shù)的共振分岔點(diǎn)變化曲線,曲線呈向右下凹形非線性變化,隨著板厚的減小,相應(yīng)的調(diào)諧值增大而出現(xiàn)共振分岔現(xiàn)象;圖8(b)和圖9(b)分別提取了圖6(b)和圖7(b)中的多值解臨界點(diǎn),繪制出磁場(chǎng)強(qiáng)度-激勵(lì)力幅值的共振分岔點(diǎn)變化曲線,曲線呈向右上非線性變化趨勢(shì),隨著磁場(chǎng)強(qiáng)度的增大,相應(yīng)的激勵(lì)力幅值增大而出現(xiàn)共振分岔現(xiàn)象,且在激勵(lì)力幅值較小時(shí),曲線斜率非常大;圖8(c)和圖9(c)分別提取了圖4(a)和圖5(a)中的多值解臨界點(diǎn),繪制出磁場(chǎng)強(qiáng)度-調(diào)諧值的共振分岔點(diǎn)變化曲線,曲線呈向右下拱形非線性變化走勢(shì),隨著磁場(chǎng)強(qiáng)度的減小,相應(yīng)的調(diào)諧值增大而出現(xiàn)共振分岔現(xiàn)象。
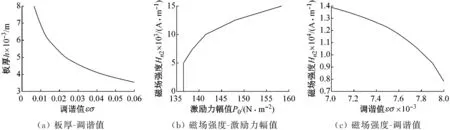
圖8 一階近似求解分岔點(diǎn)
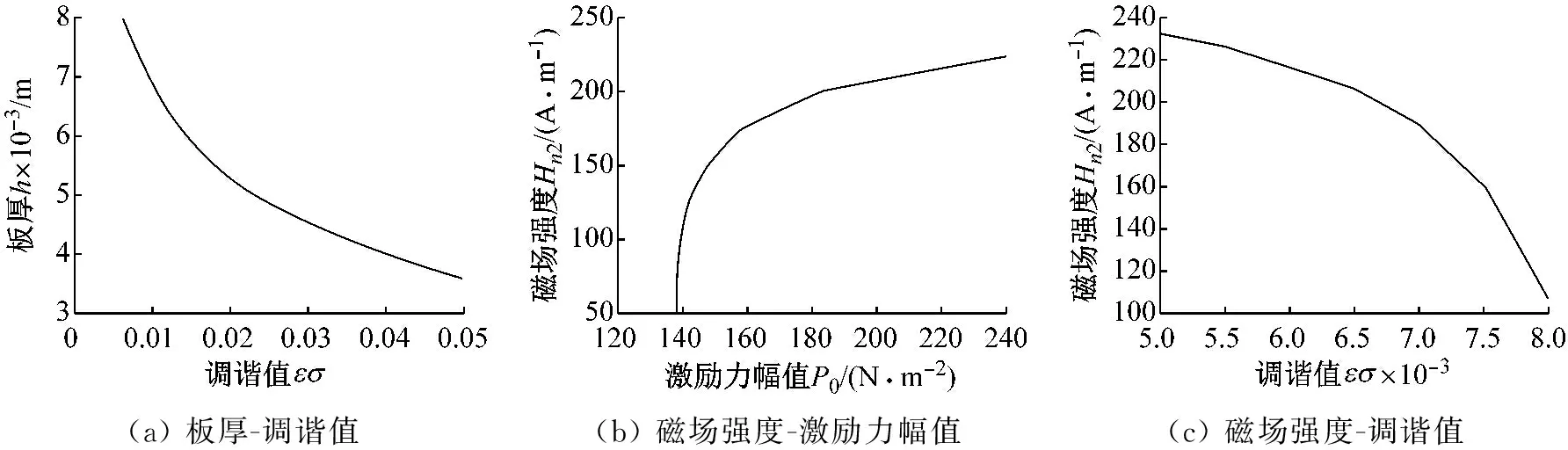
圖9 二階近似求解分岔點(diǎn)
圖10和圖11繪制了兩種求解方法下的不同參量三維曲線變化圖。由圖10(a)和圖11(a)看出,振幅隨調(diào)諧值變化時(shí),在共振區(qū)域振幅增加,且存在跳躍性,激勵(lì)力幅值變大時(shí)共振曲線整體走勢(shì)不變但共振區(qū)域拓寬。由圖10(b)可看出,一階近似下共振曲線在磁場(chǎng)強(qiáng)度較小時(shí)為分離的上下兩支曲線,當(dāng)磁場(chǎng)強(qiáng)度增大后,共振曲線變成一條曲線且最大振幅減小。由圖11(b)可看出,在二階近似下,共振曲線隨著磁場(chǎng)強(qiáng)度的增加,逐漸向另一側(cè)偏移,系統(tǒng)由硬彈簧特性變成軟彈簧特性。由圖10(c)和圖11(c)中三維曲線發(fā)現(xiàn),激勵(lì)力幅值較小時(shí),振幅-磁場(chǎng)強(qiáng)度曲線為封閉曲線與平滑曲線兩部分,隨著激勵(lì)力幅值增長(zhǎng),兩部分曲線逐漸靠近,最后合并成一條曲線。
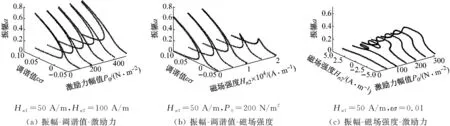
圖10 一階近似求解主共振三維圖

圖11 二階近似求解主共振三維圖
5 結(jié) 論
通過(guò)研究常磁場(chǎng)引起的靜載荷下鐵磁圓板的主共振問(wèn)題,求解出了鐵磁圓板在靜載荷下產(chǎn)生的初撓度,并應(yīng)用多尺度法,得到一階與二階近似求解下的幅頻響應(yīng)方程。
通過(guò)算例分析,得到以下結(jié)論:
(1) 當(dāng)激勵(lì)力頻率約等于圓板固有頻率時(shí),系統(tǒng)會(huì)在初撓度的基礎(chǔ)上發(fā)生主共振現(xiàn)象。當(dāng)系統(tǒng)產(chǎn)生主共振時(shí),振幅在共振區(qū)域明顯增加,且板厚、磁場(chǎng)強(qiáng)度、激勵(lì)力等參量對(duì)共振振幅產(chǎn)生顯著影響。
(2) 利用一階近似多尺度法求解時(shí),含有常磁場(chǎng)靜載的二次非線性項(xiàng)在幅頻方程中不體現(xiàn),當(dāng)磁場(chǎng)強(qiáng)度較小時(shí),一階近似與二階近似求解得到的振幅相近,而磁場(chǎng)強(qiáng)度較大時(shí),二階近似求解更為準(zhǔn)確。
- 振動(dòng)與沖擊的其它文章
- 時(shí)滯反饋對(duì)三穩(wěn)態(tài)van der Pol系統(tǒng)穩(wěn)態(tài)概率密度的影響
- 一種基于多測(cè)量向量模型的機(jī)械振動(dòng)信號(hào)聯(lián)合稀疏重構(gòu)方法
- 不同沖擊幅值下洞室圍巖變形-開(kāi)裂-垮塌過(guò)程
——基于連續(xù)-非連續(xù)方法 - 基于BOX-COX變換的橋梁結(jié)構(gòu)地震易損性分析
- 參外聯(lián)合激勵(lì)下一類(lèi)混沌系統(tǒng)的動(dòng)力學(xué)機(jī)理
- 考慮場(chǎng)地土參數(shù)隨機(jī)性和相關(guān)性的地震動(dòng)降維模擬

