面向科研訓練的算法課程教學模式

張立臣

（1.現代教學技術教育部重點實驗室，西安 710062；2.陜西省教學信息技術工程實驗室，西安 710119；3.陜西師范大學計算機科學學院，西安 710119）

0 引言

培養高層次人才一直是我國研究生培養的目標之一，而較高的科研能力是高層次人才的基本特征[1]。因此，在本科階段開展規范的科研訓練，有助于培養學生的基本科研素質和科研能力，從而為其未來從事科研工作奠定基礎。目前，以學生為中心的本科生教育教學改革，越來越突出學生的能力培養[2]。這就促使大學教師積極更新教學內容、教學模式、教學案例和教學評價方式，以培養學生包括科研能力在內的諸多能力素養。

算法課程作為計算機學科的一門專業核心課程，尤其注重培養學生算法基本理論知識和計算思維、問題建模、算法設計與分析能力[3]。算法課程在計算機學科課程中地位十分重要，其關注的算法設計與分析能力對學生未來職業發展，尤其是從事科研和算法工程師等工作，具有重要意義。因此，針對算法課程的教育教學改革受到廣泛關注，相關教材、在線課程、算法競賽層出不窮。事實上，現有的算法課程改革主要關注于算法的設計與實現，一般提供算法偽代碼或程序源代碼，但在實驗對比和分析方面較為欠缺。由此導致的結果是，學生雖然可以設計并實現教師布置的算法問題，并能夠給出正確結果，但是，所給出的結果往往是某個特定問題實例的結果，通用性較差，缺乏不同規模下的問題實例的對比結果。相反，現有算法相關論文的實驗部分大都基于不同規模的問題實例開展對比實驗，并在此基礎上，分析實驗結果，評價算法優劣。

針對上述問題，以0-1背包問題的教學為例，本文提出了一種新的算法課程教學模式，在問題建模和算法設計的基礎上，通過提供完整的編程框架和測試數據，將學生工作重心集中到算法核心代碼實現和實驗結果分析上；在此基礎上，提供矢量圖繪制模板，讓學生繪制實驗結果矢量圖并分析實驗結果。通過上述訓練，有望培養學生基本的科研素質和科研習慣，為其未來從事科研工作打下堅實基礎。

1 0-1背包問題概述

0-1背包問題是算法課程中動態規劃策略教學的重要內容[4]。0-1背包問題是一個NP難問題，解決該問題具有重要的理論和實際意義。0-1背包問題可描述為：存在1個有限容量的背包和一組有限個數的物品，已知背包的容量以及每個物品的重量和價值，如何選擇裝入背包的物品，使得在不超過背包容量的前提下，裝入背包的物品的總價值最大。該問題的形式化數學模型可用0-1整數規劃模型描述：

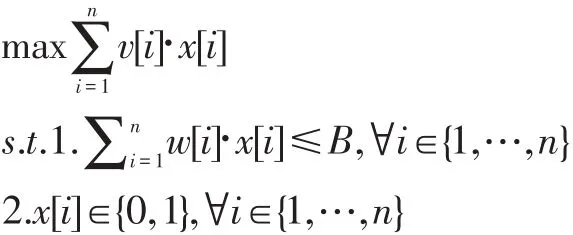
其中，w[i]和v[i]分別表示物品i的重量和價值，B表示背包的容量，x[i]表示是否將物品i放入背包，x[i]=1表示裝入物品i，x[i]=0表示不裝入物品i，其中，i∈{1,…,n}。

現有教材一般采用動態規劃算法策略求解該問題，動態規劃算法適合那些經分解得到的子問題不互相獨立的情形。0-1背包問題的動態規劃算法的遞推方程為：

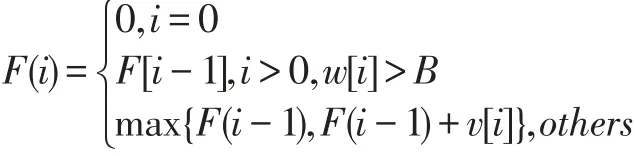
其中，F（i,W）表示在不超過背包容量W的前提下，選擇前i個物品中的某些物品（i≤n）所得到的最大價值，即F（i,W）對應的子問題是由前i個物品及容量為W的背包構成的。

分析上述遞推方程，學生一般能夠通過循環、分支等語句完成程序源代碼編寫并調試運行。但是，這在實驗對比方面較為欠缺，學生一般不進行不同問題規模下的實驗對比和分析。為此，我們針對該問題設計了新的教學模式，以訓練和培養學生基本的實驗對比和分析能力。

2 聚焦實驗對比和分析的0-1背包問題教學模式

在對0-1背包問題進行數學建模和動態規劃算法設計的基礎上，我們提供了實現該問題的編程框架和測試數據，以突出訓練和培養學生的核心代碼編寫和實驗結果分析能力。

2.1 協作結對編寫算法核心代碼

協作結對編程是指兩個程序員共同完成同樣的編程任務，有助于減少學生的認知負荷，提升學生的互動性和學習興趣[5]。學生自由組合結對，在課堂上共同操作一臺電腦完成核心代碼的編寫和調試。為了將學生聚焦于核心代碼編寫層面，我們設計了程序框架，并讓學生提前下載到電腦中。所提供的程序框架采用Java語言編寫，以Eclipse項目形式提供下載，0-1背包問題編程框架如下所示：

代碼塊1：文件Test.Java:

代碼塊2：文件Knapsack.Java

以上代碼提供了2個文件，其中，文件Test.Java用于產生輸入數據、輸出結果，文件Knapsack.Java用于解決0-1背包問題。在文件Test.Java中，定義了物品重量數組、物品價值數組和背包容量等全局變量，這些數據通過函數generate（）隨機產生，共產生10組數據，物品價值和重量在1至10之間，背包容量限制為物品總重量的0.8倍。第一組數據包括10個物品，然后以10的倍數增加物品數量。對每組產生的數據，將調用Knapsack類中的靜態方法solve（），該方法需要學生結對編程實現。此外，為了記錄動態規劃算法的時間，用數組ctime記錄處理每組數據所用的時間并輸出。一種可行的動態規劃源代碼如下所示。

代碼塊3：

開始時，學生將實驗次數num的值先設置為1，然后通過斷點或輸出以檢查所設計的算法是否正確，在正確的前提下，將實驗次數增加，記錄所需的時間。

2.2 分析實驗數據

在保證算法正確的前提下，學生分析實驗結果。通常，由于當前電腦速度極快且數據規模較小，每組實驗所消耗的時間差別不大，有時實驗在某些規模下所耗時間反而降低。針對此問題，一般通過兩種方式實現。一種是調整實驗參數，通過增加數據規模，比如將物品的數量從300開始增加，依次增加300；一種是對每次實驗重復多次，取平均時間。此外，在實驗中也可以同時結合這兩種方式。

在此基礎上，分析影響實驗結果的因素。由于0-1背包問題的動態規劃算法的時間復雜度為O（n*B），其中n和B分別是物品的數量和背包的容量。因此，背包容量B也會影響算法性能，可以通過設置不同的背包容量，記錄實驗的運行時間，并作出適當分析。

2.3 繪制矢量圖并分析實驗結果

圖和表格是常見的兩種實驗結果的呈現方式。鑒于圖更為直觀和常用，我們提供了矢量圖的繪制命令模板。首先，學生下載并安裝矢量畫圖工具Gnuplot（http://gnuplot.sourceforge.net/）；然后，將每組實驗記錄的運行時間數據按列形式存在數據文件中，如data.txt，格式如表1所示；接著，修改如代碼塊4所示的命令文件a.txt；最后，在Gnuplot軟件命令行中，通過load“a.txt”執行命令，矢量圖eps文件（如圖1所示）被生成于命令文件所在的文件夾中。

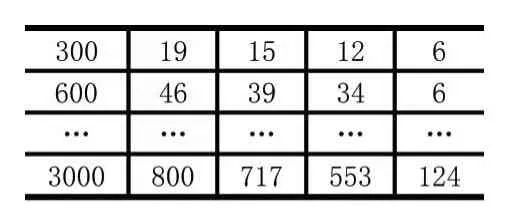
表1 實驗產生的數據文件

表1中的第1列表示數據規模，即物品數量，從物品數量為300開始，以300增加，最終到3000；從第2列起每列代表一個算法在各個規模下的數據下的運行時間，共 4個算法，分別記為 DP-0.9、DP-0.7、DP-0.5、GR-0.9，其中，DP表示動態規劃算法，GR表示貪心算法，后面的數字表示背包容量占物品總重量的比重，比如0.9表示背包容量是所有物品重量之和的0.9倍；單元格中的數據是算法的運行時間，單位是毫秒（ms）。代碼塊4給出了繪制矢量圖的命令文件的內容，其中，符號#后面是簡要解釋。依據代碼塊4的命令和表1的數據，通過Gnuplot執行，可生成圖1所示的矢量圖。

代碼塊4：

需要指出的是，貪心算法GR-0.9是按照單位價值比從大到小處理的。從圖1可以看出，貪心算法運行時間明顯小于各個動態規劃算法，而動態規劃算法隨著背包容量增大、物品數量增加，其運行時間逐漸增加，基本呈現線性增長方式，這與理論上的時間復雜度相同。此外，學生還可以修改源代碼，課下開展動態規劃算法和貪心算法的優化目標比較，從中發現貪心算法的近似最優特性及其與動態規劃算法的差距。

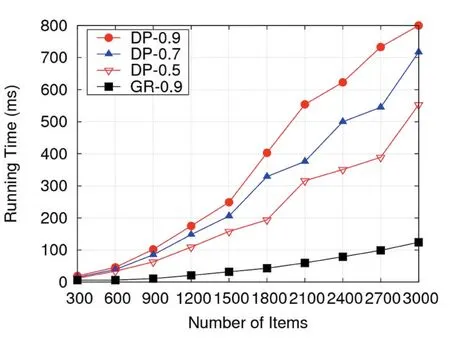
圖1 0-1背包問題的各類算法的運行時間對比圖

2.4 對比多種算法

0-1背包問題是經典的NP難問題，動態規劃算法和貪心算法只是求解該問題的常用算法。隨著算法課程的開展，其他算法，如回溯法、分支限界法、概率算法將陸續被介紹。通過保留上述實驗數據和相關Gnu?plot繪圖命令，待掌握其他算法之后，再進行對比，從中發現新規律，可以加深各個算法策略的理解和應用。此外，上述實驗流程和分析也將為學生開展實際問題的算法研究提供新思路。

3 結語

本文以培養學生實驗對比和分析能力為目標，以算法課程中的0-1背包問題為例，提出了新的教學模式，引導學生開展協作結對編程、實驗數據產生、矢量圖繪制、實驗結果分析等較為規范的科研訓練。本文所提出的科研訓練模式可以讓學生加深對算法策略的理解和綜合應用，有望為學生未來順利開展科研工作奠定基礎，同時也為以能力目標導向的算法課程教學改革提供新思路。