京滬高鐵隧道背景下列車車體動態氣密性當量泄漏面積閾值特征
萬有財, 李 明, 張 雷, 劉 斌, 梅元貴
(1.蘭州交通大學 甘肅省軌道交通力學應用工程實驗室,蘭州 730070;2.中車唐山機車車輛有限公司,河北 唐山 064099)
高速列車通過隧道誘發車外劇烈壓力波動,車外壓力波動通過車門、車窗、空調通風口以及地板穿線孔等部件不規則長度各異的縫隙傳入車內,引起司乘人員耳感不適問題[1-2]。為保證車內人員壓力舒適性,除采取加大了隧道凈空面積措施外,在列車方面采取了氣密性車體和加裝了壓力保護裝置。用來描述列車氣密性的常用物理量是時間常數和當量泄漏面積兩個氣密參數。目前各國采用靜態時間常數來規定高速列車的氣密性:日本和法國等規定車內壓力由4 000 Pa降至1 000 Pa的時間必須大于50 s;德國和意大利規定車內壓力由3 600 Pa降至1 350 Pa的時間必須大于18 s;中國規定[3]車內壓力由4 000 Pa降至1 000 Pa的時間必須大于40 s(速度等級在200 km/h~250 km/h)和50 s(速度等級在250 km/h~350 km/h)。時間常數雖能以車內壓力泄壓時間的長短簡潔地表示車體氣密性的好壞,但物理意義并不直接明了,對優化列車各部件的氣密性、空調通風和壓力保護技術系統的比選和設計缺乏一定的定量指導價值。氣密性車體會較大幅度的提高列車制造和維護成本,根據壓力舒適性要求,確定車體氣密性值,對合理設計和運營維護列車有直接的指導意義。
列車通過隧道引起的壓力波要比明線交會壓力波要劇烈得多,是評價和考核耳感舒適性問題的主要工程場景。國內外學者針對列車通過隧道時車外壓力波問題主要利用實車試驗、模型試驗和數值仿真等技術展開研究[4-5]。尤其是一維流動模型特征線數值模擬方法被得到廣泛應用:Vardy[6-7]基于一維可壓縮非定常等熵流動模型發展起來的Thermo Tun[8]商業軟件;Woods等[9-11]采用一維可壓縮非定常不等熵流動模型研究壓力波。針對車內壓力:Yamamoto[12]根據車內外空氣質量交換實際特征和質量守恒定律,提出“當量泄漏面積”表示車體氣密性方法,并給出考慮列車通風實際特點的車內壓力計算模型;Klingel[13]考慮車體壓縮性采用細長孔泄漏模型,提出“時間常數”表示車體氣密性方法,并建立了車內壓力計算模型;Sima等[14-15]考慮車體壓縮性并結合細長孔和薄壁孔兩種不同泄漏模型建立了“C1、C2參數法”計算車內壓力;張光鵬等[16]建立“熱力學模型”計算車內壓力;閆亞光等[17]采用三維數值模擬研究了兩列車隧道內交會時,列車速度、列車長度、密封性及隧道內不同會車位置對車內壓力變化最大值的影響。上述研究工作從不同角度重點研究了車內外壓力,但未對列車的氣密性閾值展開研究。
Nam[18]未考慮車體壓縮性采用時間常數評價了列車氣密性;Sima等[19]利用實車試驗測得的車內外壓力數據采用試湊法得出了動態時間常數和泄漏面積值;余南陽等[20]以京滬線為背景,利用時間常數研究車內壓力及舒適性特征;李國清等[21]采用靜態試驗采用當量泄漏面積對高速綜合檢測列車車體密封進行了評估;許良中等[22]基于實車試驗測得的車內外壓力,分析了單車明線工況下車體動態時間常數隨時間的變化關系,針對旅客耳感不適問題提出了改進措施;梅元貴采用時間常數針對特長隧道耳感不適問題進行了研究,建議在特長隧道條件下采用多時間間隔壓力變化閾值來評價耳感舒適性;史憲明等[23]采用一維特征線法,以時間常數表征動車組氣密性能,研究了不滿足車內壓力舒適性標準的隧道長度區間;張芯茹等[24-25]等基于壓力舒適性標準,采用數值模擬方法研究了列車的動態氣密時間常數閾值。
從國內外目前研究看,盡管提出了不同速度等級的高速列車車體氣密性的要求,但結合舒適性標準、實際隧道壓力波特征等,研究車內壓力特征,提出動態當量泄漏面積的閾值要求的成果未見到公開報道。京滬客運專線是我國高速鐵路發展的代表,目前商業運營速度已達到350 km/h,本文以京滬客運專線為背景,基于一維可壓縮不等熵非定常流動模型的廣義黎曼變量特征線法數值模擬得到車外壓力;未考慮車體壓縮性,選用薄壁孔流動模型,建立車內外壓力關系—“當量泄漏面積法”,利用改進歐拉法求解微分方程得到車內壓力;基于500 Pa/s、800 Pa/3 s和1 000 Pa/10 s三種車內壓力舒適性標準,從動車組編組長度、速度和通過方式三方面對中國某型號標準動車組動態氣密性展開研究,給出動車組在不同速度等級下單節車廂動態當量泄漏面積閾值的建議值,為動車組氣密性設計提供基礎性技術參考。
1 研究方法
本文利用數值模擬方法求解車外壓力;基于靜態試驗數據驗證了本文所建立的計算車內壓力方法的合理性及程序的準確性;在滿足壓力舒適性標準的條件下,數值求解動態當量泄漏面積閾值。
1.1 物理模型
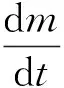

圖1 等效泄漏模型示意圖
1.2 車外壓力波數值計算方法
動車組通過隧道所引起的三維流動可簡化為一維可壓縮非定常流動,考慮到隧道內空氣與動車組壁和隧道壁之間存在摩擦和傳熱,流動是不等熵的,所以本文采用一維可壓縮非定常不等熵流動模型[26]來求解車外壓力。描述流動的控制方程如下
連續性方程
(1)
動量方程
(2)
能量方程
(κ-1)ρ(q-ξ+uG)
(3)
式中:u、p、κ、ρ和a分別為隧道內空氣流速、壓力、比熱比、密度和聲速;F為空氣流道橫截面面積;G為空氣與壁面的摩擦項;q為空氣與壁面的傳熱項;ξ為空氣與列車壁面的摩擦功;t為時間。式(1)~式(3)構成了一階擬線性偏微分方程組,利用廣義黎曼變量特征線方法求解。
1.3 車內壓力求解方法
列車過隧道車廂內外存在壓差,通過車廂泄漏孔存在向內充氣和向外漏氣兩種過程,充氣或漏氣過程的空氣為理想氣體的絕熱等熵流動,忽略車體變形,利用伯努利方程得到空氣流速
(4)
空氣的質量流量為
(5)
在絕熱充氣/漏氣過程中,車廂內壓力變化率和流入/流出的空氣質量流量有以下關系
(6)
結合式(4)~(6),再根據聲速公式a2=κ·Rg·T得出計算車內壓力式(7),計算車內壓力時,初始時刻車內壓力值取零時刻的車外壓力值,文中在已知車廂外壓力的條件下,采用改進的歐拉法求解式(7)得到車內壓力
(7)
文中采用數值方法求解車外壓力時,選取的時間步長很小,由流場的連續性可知,壓力不會突變,故可認為在較短時間內車外壓力變化較小,基本保持不變,假設車外壓力在Δt(Δt=t2-t1)時間內是幾乎不變的,積分式(7)后變形可得當量泄漏面積的計算式
(8)
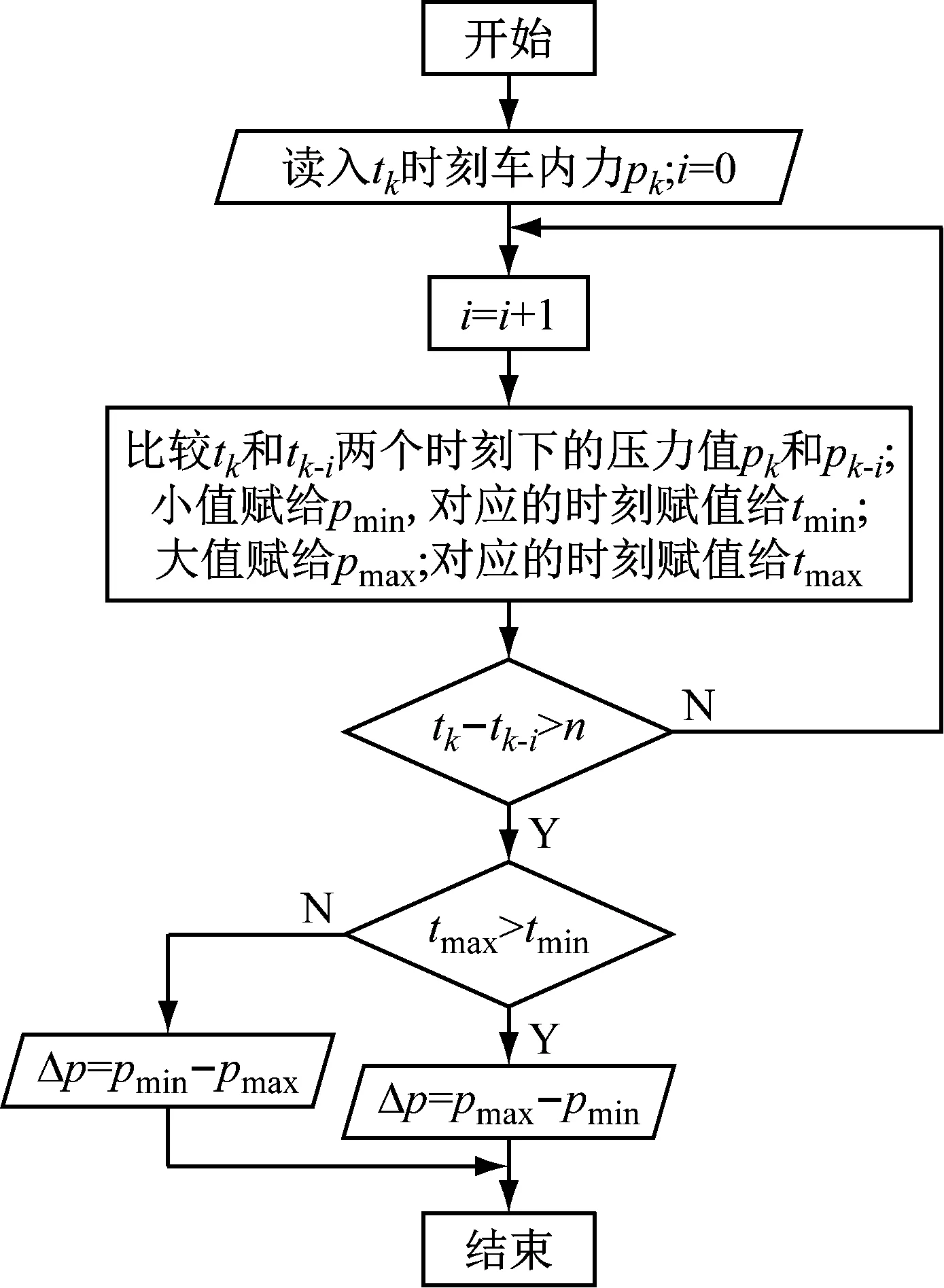
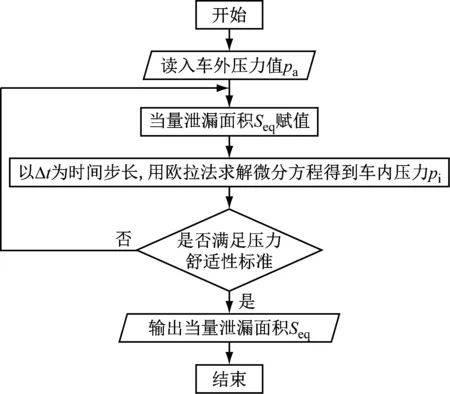
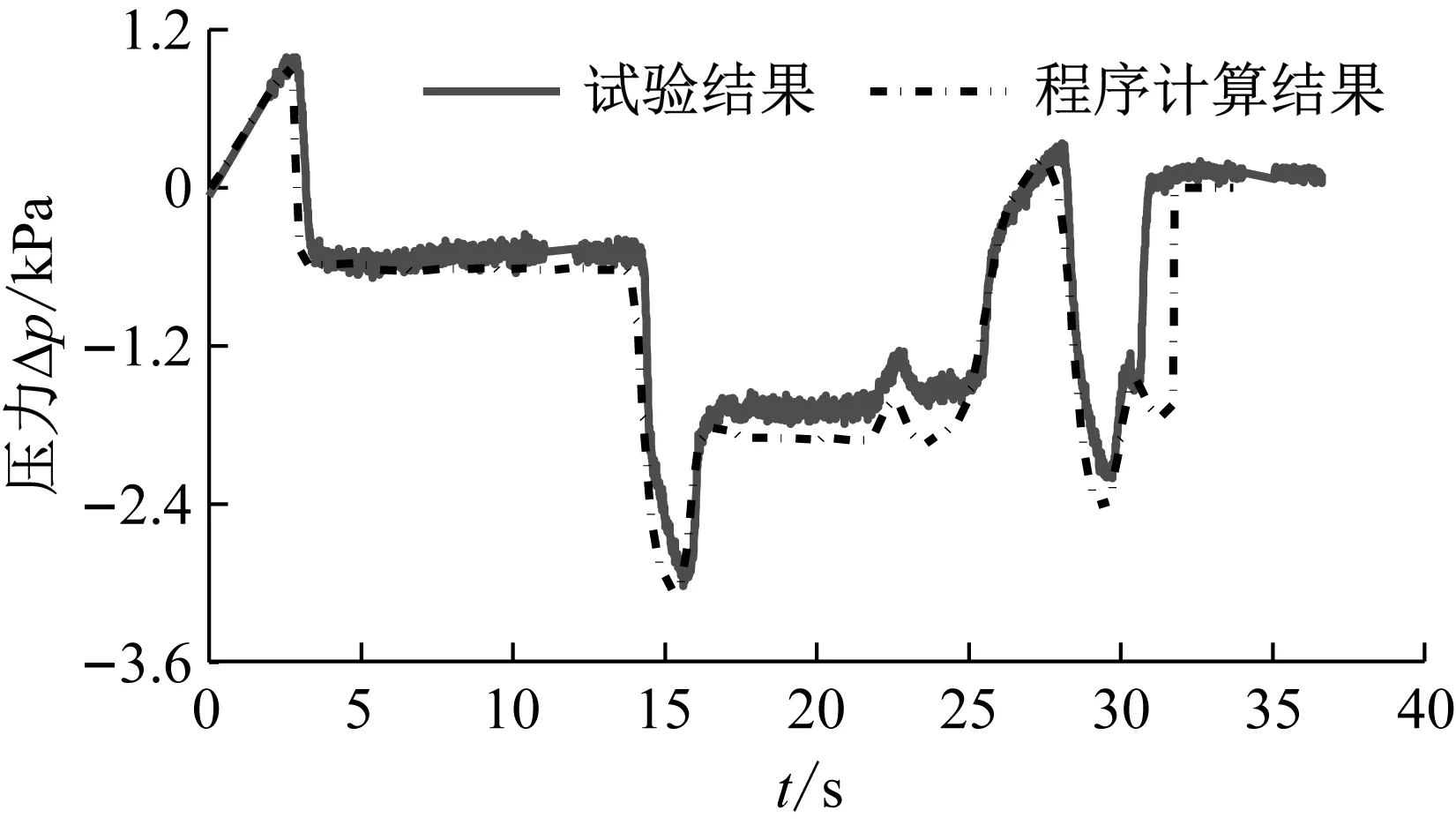
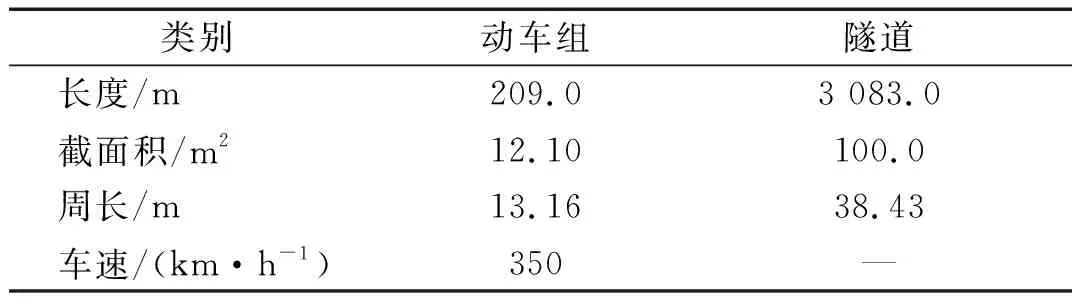
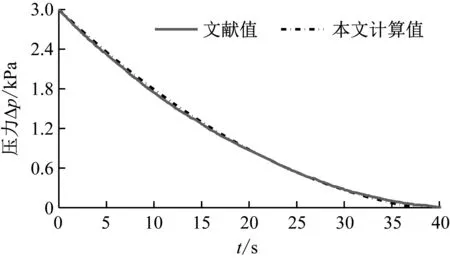
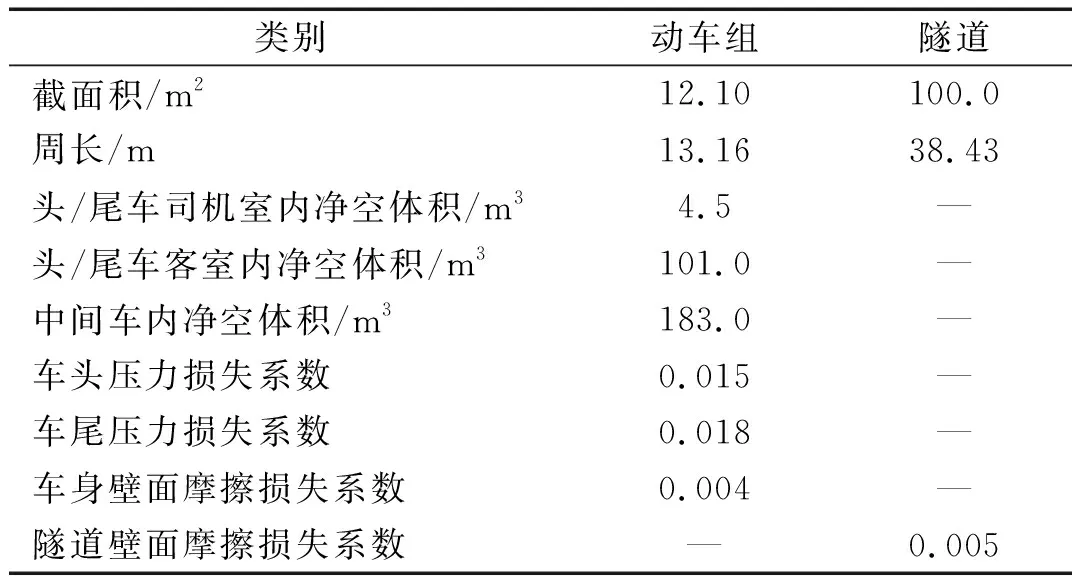
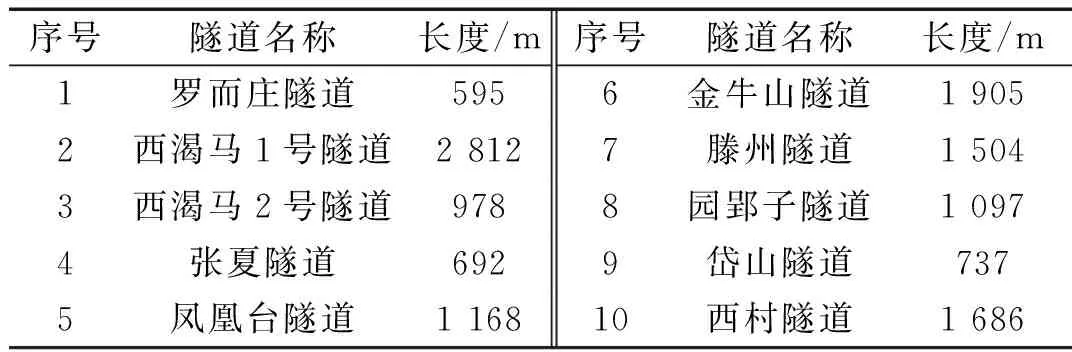
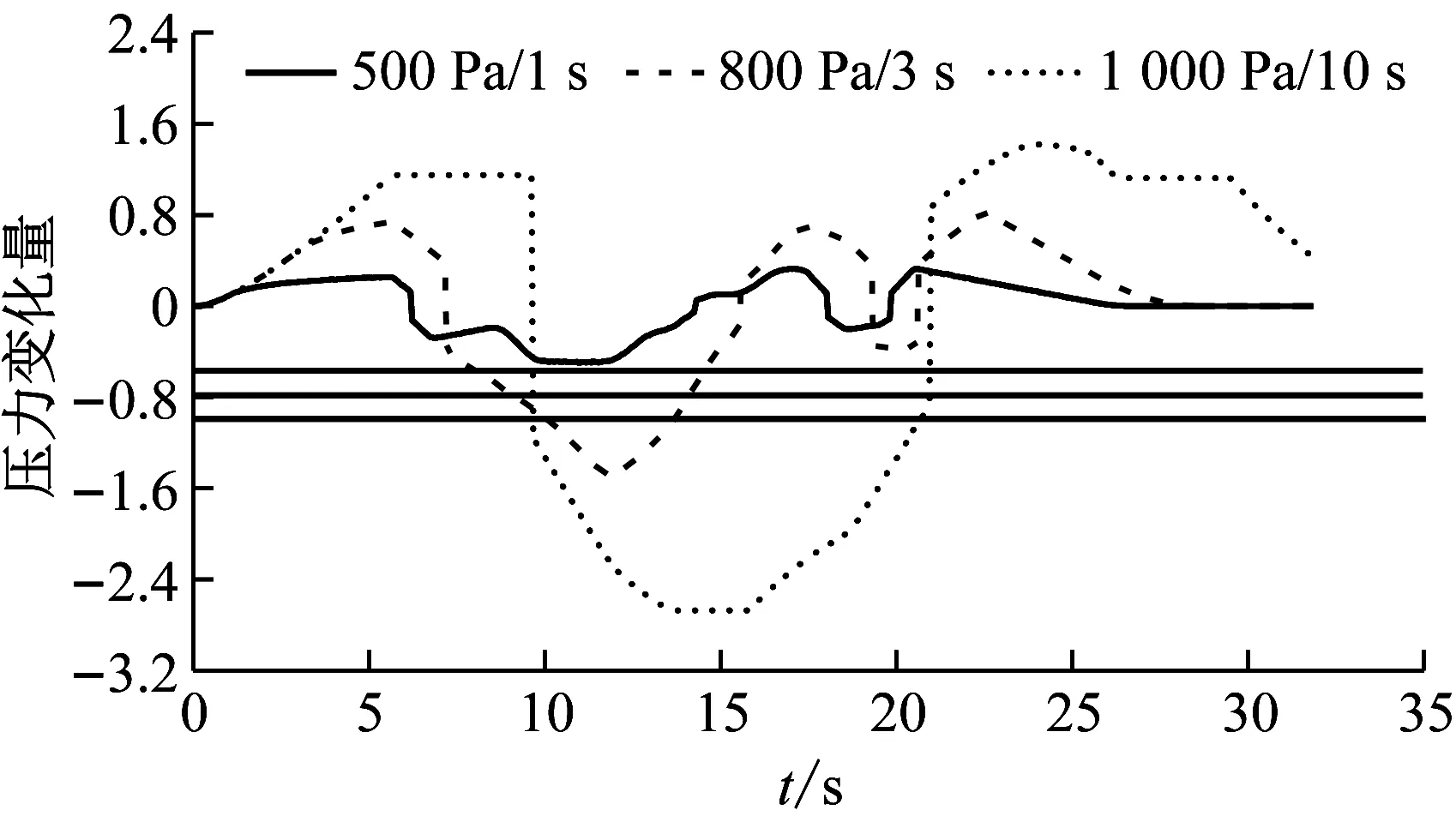
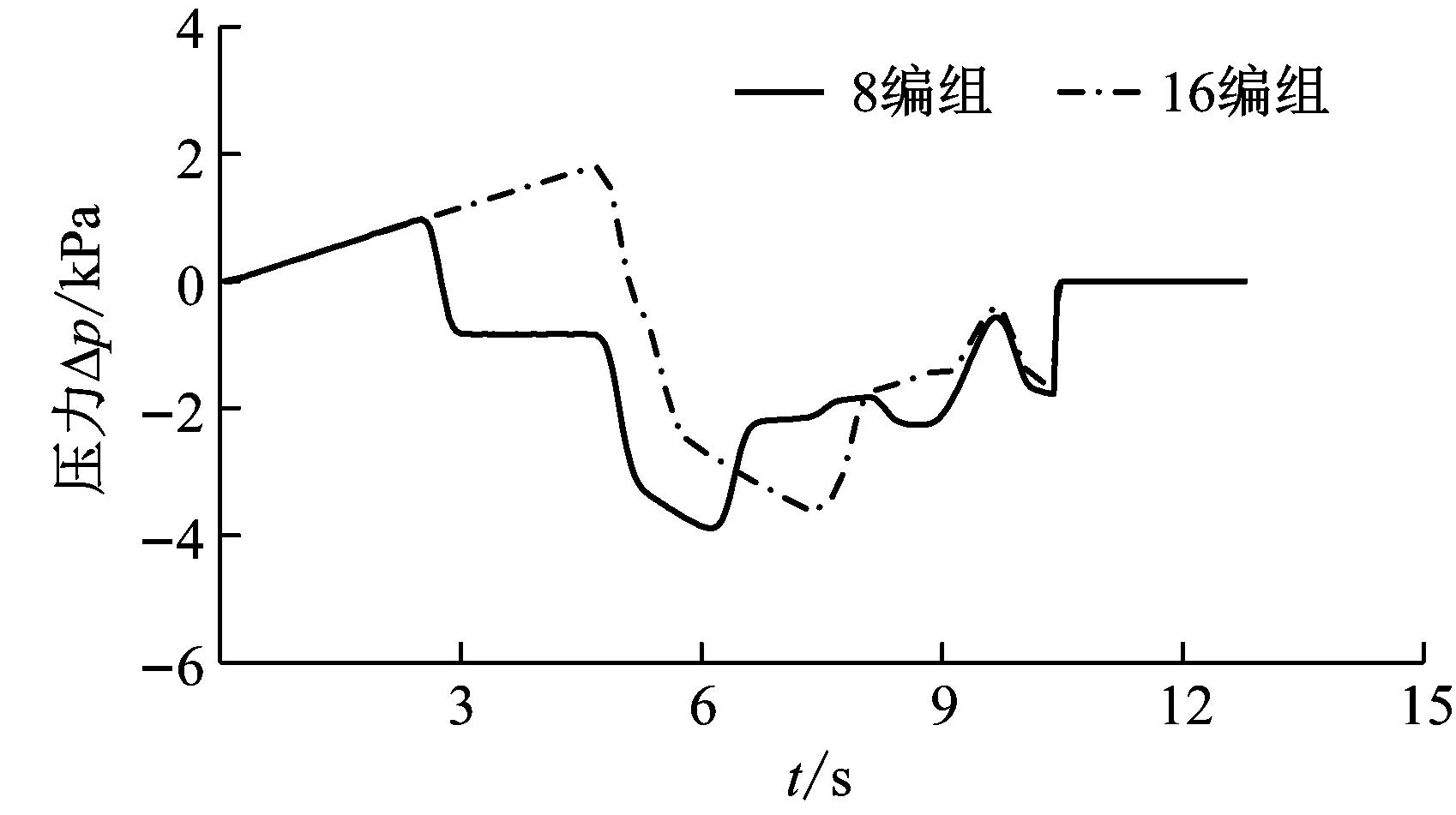
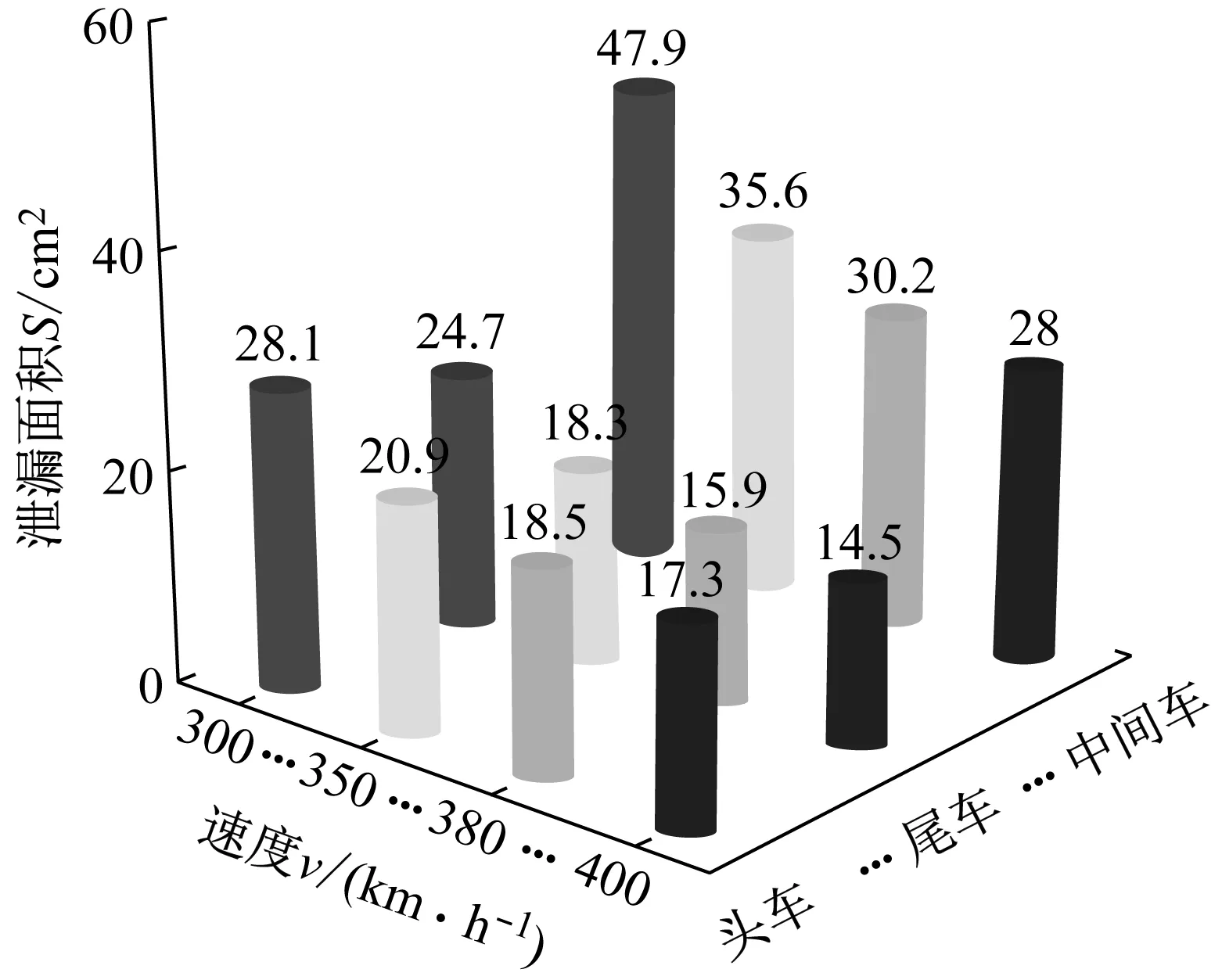
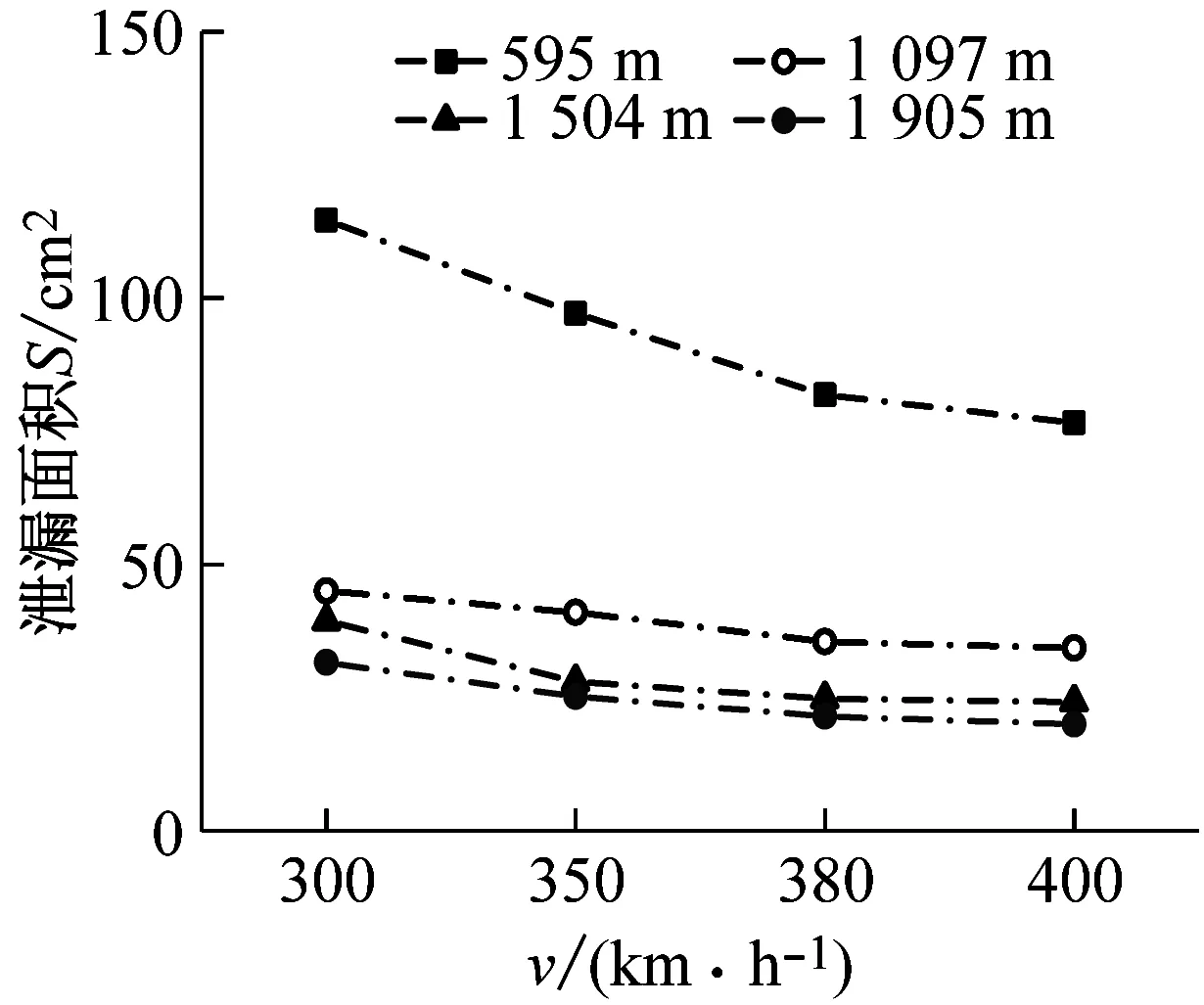
式(4)~(8)中:Δp=pi-pa,pi和pa分別為車廂內外壓力值;a、κ、T、ρ和Rg分別表示空氣聲速、比熱比、溫度、密度和氣體常數;t為時間;V為每節車廂的內部凈空體積;Seq為單節車廂總當量泄漏面積;式(7)中負號表示漏氣:pi>pa;正號表示充氣:pi 根據車外壓力值,結合1.3節介紹的方法可計算得到各個時刻的車內壓力值,車內外壓力均可看作關于時間t的連續函數。圖 2給出了統計任一tk時刻車內不同時間間隔內最大壓力變化量的流程圖。n表示不同的時間間隔,t1和t2時刻對應的車內壓力值分別為p1和p2,假使最終確定出最大壓力值為p1,最小壓力值為p2。若t1>t2,則每n秒內的最大壓力變化量Δp=p1-p2,表示該時間段內車內壓力最大值出現在最小值之后;若t1 圖2 統計車內不同時間間隔內最大壓力變化量流程圖 圖3給出了車廂當量泄漏面積閾值的估算流程圖。由圖3可知:已知車外壓力,先估算一個當量泄漏面積值,根據車外壓力利用式(7)求解得到車內壓力;根據求解的車內壓力,計算車內不同時間間隔內最大壓力變化量,對比車內不同時間間隔內最大壓力變化量的最大值是否符合對應車內壓力舒適性標準允許的最大值,若符合對應的舒適性標準,則所估算的當量泄漏面積值即為對應的當量泄漏面積閾值,若不符合對應的舒適性標準,循環此過程估算當量泄漏面積直至符合壓力舒適性標準。 圖3 估算車廂當量泄漏面積閾值流程圖 本文采用可壓縮不等熵非定常流動模型的廣義黎曼變量特征線法源代碼程序模擬車外壓力,圖 4給出了單列CRH400BF動車組通過大西線忻州隧道時,頭車中部測點的實車試驗結果與一維程序結果對比,縱坐標Δp表示車外壓力相對于大壓力的相對值,表1給出了實車試驗基本參數。數值計算得到的車外壓力波動趨勢與實車試驗結果吻合度良好,頭車平直車身中部測點最大正負壓值與實車試驗的誤差分別1.49%和4.47%。計算精度可滿足工程需求,說明了本文車外壓力數值模擬方法的合理性和程序的準確性。 圖4 計算車外壓力程序驗證 表1 實車試驗基本參數 本文利用Sima給出的靜態泄壓試驗數據來驗證計算車內壓力方法的合理性和程序的準確性。結果如圖5所示,縱坐標Δp表示靜態泄壓實驗時車廂內壓力相對于車廂外壓力的相對值,車廂泄漏面積為16.5 cm2。本文計算結果在12.5 s左右達到最大誤差3.4%,與文獻試驗結果相比,吻合度良好,說明本文車外壓力數值模擬方法的合理性和程序的準確性。 圖5 計算車內壓力程序驗證 (1) 計算參數 本文以中國某型號標準動車組為研究對象,動車組和隧道的具體參數見表2,本文研究頭/尾車的氣密性時,將頭/尾車的客室和司機室內的凈空體積進行了相加。 表2 動車組與隧道基本參數 京滬線上共有22座隧道,總長度16 km,本文選擇了隧道長度大于500 m的10座隧道展開研究,表3給出10座隧道的具體名稱和對應長度。 表3 京滬線部分隧道 (2) 舒適性標準 本文研究動車組的最低速度為300 km/h,且京滬線上最長的隧道為2 812 m,16編組動車組全程通過時間不到40 s,所以本文選用UIC中規定的多時間間隔下的三個壓力舒適性標準:500 Pa/s、800 Pa/3 s和1 000 Pa/10 s。 為了闡明車內外壓力波的形成機理,圖 6表示兩列16編組動車組以350 km/h的速度在西渴馬1號隧道中央等速交會時車內外壓力及車內每3 s內最大壓力變化量時間歷程曲線。滿足車內最大壓力變化幅值≤800 Pa/3 s時頭、尾車當量泄漏面積閾值分別為30.0 cm2和32.6 cm2。 圖 6(a)表示頭尾車通過隧道誘發的壓縮波和膨脹波的軌跡線,車頭和車尾鼻尖運行軌跡,黑色實線/劃線分別表示車頭/尾鼻尖運動軌跡。紅色(綠色)實線和短劃線分別表示壓縮波和膨脹波軌跡線。圖 6(b)和(c)中垂直于橫坐標的紅色(綠色)實線和短劃線分別表示壓縮波和膨脹波,垂直橫坐標的黑色實線和黑色劃線分別表示兩列動車組頭頭交會和尾尾交會瞬間。“C”表示壓縮波,“E”表示膨脹波,“N”表示車頭,“T”表示車尾;例如,“C1N”和C2N分別表示第一列動車組和第二列動車組的車頭駛入隧道入口端產生的初始壓縮波,“E1N”和E2N分別表示該初始壓縮波在隧道端口經過一次反射后形成的膨脹波,“C1N1”和“C2N1”分別表示該初始壓縮波在隧道端口經過兩次反射后形成的壓縮波。圖 6(b)和(c)中左側縱坐標Δp表示車外壓力相對于大壓力的相對值,文中后續出現的車外壓力值均是相對于大氣壓力的相對值。 由圖 6(b)和(c)可知;動車組在隧道內交會的車外壓力波動,是壓縮波和膨脹波共同作用的結果—車身測點遇壓縮波壓力升高,車身測點遇膨脹波壓力下降。動車組在隧道中央等速交會,頭車車外壓力呈“先正后負”、尾車呈“先負后正再負”的規律。車外壓力波動通過車廂的縫隙傳入車內引起車內的壓力波動,車內壓力波動趨勢與車外一樣,由于動車組有一定的密封性,使得車內壓力的波動幅值明顯小于車外的。由圖 6(b)和(c)可知:頭尾車車內每3 s內最大壓力變化量均在18 s左右達到規定的閾值,若車廂泄漏面積大于泄漏面積閾值,車內壓力便不能滿足800 Pa/3 s壓力舒適性標準。 動車組以同一速度通過不同隧道,當車內壓力符合同一種舒適性標準時,便會產生不同的當量泄漏面積閾值。本文把同一編組動車組以同一速度通過不同長度隧道時,車內壓力符合同一種舒適性標準時產生的當量泄漏面積閾值中最小的稱為“當量泄漏面積閾值的最小值”。 (a) 列車運行軌跡圖和波反射圖 (b) 頭車 (c) 尾車 圖7表示16編組動車組通過以350 km/h速度通過1 905 m隧道時,頭車當量泄漏面積分別取25.2 cm2(符合1 000 Pa/10 s標準時的當量泄漏面積閾值)和87.9 cm2(符合500 Pa/s標準時的當量泄漏面積閾值)時,車內每1 s、3 s和10 s內最大壓力變化量時間歷程曲線。圖中平行于橫坐標的三條實線表示500 Pa/s、800 Pa/3 s和1 000 Pa/10 s的閾值。由圖7可知:當量泄漏面積為25.2 cm2時,車內每1 s、3 s和10 s的最大壓力變化量均分別小于其閾值500 Pa、800 Pa和1 000 Pa;當量泄漏面積為87.9 cm2時,車內每1s的最大壓力變化量小于其閾值500 Pa,而車內每3 s和10 s的最大壓力變化量均分別大于其閾值800 Pa和1 000 Pa。這說明滿足車內壓力1 000 Pa/10 s標準時的當量泄漏面積閾值也會滿足其它兩個標準。 五個流態化反應器串聯在一起形成環形系統,當首槽料層含鎘達85%以上或尾槽后液鎘持續超出0.001g/L,首槽退出,其后反應器作首槽,新并入反應器作尾槽。 (a) 當量泄漏面積Seq=25.2 cm2 (b) 當量泄漏面積Seq=87.9 cm2 圖8表示16編組動車組以350 km/h的速度通過692 m、1 097 m、1 504 m和1 905 m四個不同長度隧道,頭中尾車內壓力符合三種不同舒適性標準時的當量泄漏面積閾值變化曲線,由圖 8可知:動車組以350 km/h速度通過同一隧道時,車內壓力符合不同舒適性標準的當量泄漏面積閾值不同,且當量泄漏面積閾值按符合500 Pa/s、800 Pa/3 s 和1 000 Pa/10 s標準依次減小。 (a) 頭車 (b) 中間車 (c) 尾車 表4統計了16編組動車組以350 km/h速度通過京滬線長度大于500 m的10個隧道,車內壓力符合三種不同舒適性標準的當量泄漏面積閾值的最小值。由表 4可知:車內壓力符合1 000 Pa/10 s標準時,取得當量泄漏面積閾值的最小值,所以本文后續著重以1 000 Pa/10 s的標準展開研究。 表4 不同舒適性標準下當量泄漏面積閾值的最小值 圖9表示8編組和16編組動車組分別以380 km/h的速度通過692 m、1 097 m、1 504 m和1 905 m四個不同長度隧道,頭中尾車內壓力符合1 000 Pa/10 s標準時的當量泄漏面積閾值變化曲線。由圖 9可知:8編組動車組通過692 m、1 097 m和1 504 m三個隧道,車內壓力符合1 000 Pa/10 s標準時取得的當量泄漏面積閾值比16編組的小。由圖 9(a)可知:8編組和16編組動車組以380 km/h的速度通過1 097 m隧道,車內壓力滿足1 000 Pa/10 s標準時頭車當量泄漏面積閾值均小于45.0 cm2,但8編組的比16編組的小。 (a) 頭車 (b) 中間車 (c) 尾車 為分析說明8編組動車組車體當量泄漏面積閾值為何小于16編組的,圖10表示8編組和16編組單列動車組以380 km/h的速度通過1 097 m隧道時,頭車車外壓力和頭車(當量泄漏面積為均45.0 cm2)內每10 s內最大壓力變化量隨時間的變化曲線。由圖 10可知:16編組動車組的頭車外最大壓力峰峰值比8編組的大;當8編組動車組和16遍組動車組的頭車當量泄漏面積一樣時,8編組動車組頭車內每10 s的最大壓力變化量的最大負壓值卻比16編組的大。所以8編組和16編組動車組以380 km/h的速度通過1 097 m隧道,當頭車內壓力同時滿足1 000 Pa/10 s標準時,8編組動車組的頭車當量泄漏面積閾值必然要小于16編組的,符合圖 9(a)中藍色點劃線變化趨勢。 (a) 車外壓力 (b) 車內每10 s內最大壓力變化量 表5統計了不同編組單列動車組以380 km/h速度通過京滬線長度大于500 m的10個隧道,車內壓力符合三種不同舒適性標準的當量泄漏面積閾值的最小值。由表 5可知:16編組動車組符合800 Pa/3 s和1 000 Pa/10 s兩個壓力舒適性標準時的當量泄漏面積閾值的最小值小于8編組的;而8編組動車組符合500 Pa/s壓力舒適性標準時的當量泄漏面積閾值的最小值小于16編組的。 表5 不同編組單列動車組當量泄漏面積閾值的最小值 圖11表示16編組動車組以300 km/h、350 km/h、380 km/h和400 km/h四種速度通過2 812 m隧道,車內壓力符合1 000 Pa/10 s標準時的當量泄漏面積閾值隨車速的變化規律。由圖 11可知:當量泄漏面積閾值隨著車速的增加而減小;中間車的當量泄漏面積比頭尾車的大。以中間車為例,動車組速度從350 km/h增加到400 km/h,動車組速度增加了14.3%,當量泄漏面積閾值從35.6 cm2減小到28.0 cm2,當量泄漏面積閾值反而減小了21.3%;動車組速度為350 km/h時,中間車的當量泄漏面積閾值比頭車和尾車的分別大41.3%和94.5%。 圖12表示16編組動車組以300 km/h、350 km/h、380 km/h和400 km/h四種速度通過595 m、1 097 m、1 504 m和1 905 m四個不同隧道,車內壓力符合1 000 Pa/10 s舒適性標準時,頭尾車和中間車當量泄漏面積閾值變化曲線。由圖12可知:在符合車內壓力舒適性標準的條件下,動車組以不同速度通過同一隧道,車速越高車廂當量泄漏面積閾值越小。 圖11 當量泄漏面積閾值隨動車組速度變化規律 表6統計了單列16編組動車組以四種不同速度通過京滬線長度大于500 m的10個隧道,車內壓力符合三種不同舒適性標準的當量泄漏面積閾值的最小值。由表 6可知:滿足三種不同壓力舒適性標準的當量泄漏面積閾值的最小值均隨著動車組速度的增加而減小。 (a) 頭車 (b) 中間車 (c) 尾車 圖13表示16編組動車組以400 km/h的速度單列車通過和隧道中央等速交會通過1 097 m、1 504 m、1 905 m和2 812 m四個不同長度隧道,車內壓力符合1 000 Pa/10 s標準時,頭尾車和中間車當量泄漏面積閾值變化曲線。由圖13可知:16編組以400 km/h的速度在四個隧道內中央等速交會時的當量泄漏面積閾值比單列車通過時的小。 表7統計了16編組動車組以四種速度中央等速交會通過京滬線上隧道長度大于900 m的7個隧道,車內壓力符合三種不同舒適性標準的當量泄漏面積閾值的最小值。結合表6和表7的統計結果,表 8最終給出了16編組動車組在不同速度等級下以不同方式通過京滬線上部分隧道,車內壓力符合不同壓力舒適性標準時的當量泄漏面積閾值的建議值。由表 8可知:當量泄漏面積閾值的最小值隨著車速的增加而減小,且四種速度下均在符合1 000 Pa/10 s舒適性標準時取得對應最小當量泄漏面積的建議值。 (a) 頭車 (b) 中間車 (c) 尾車 表7 16編組動車組以不同速度在隧道中央等速交會當量泄漏面積閾值的最小值 表8 當量泄漏面積建議值 本文選用薄壁孔流動模型,建立“當量泄漏面積法”,基于車內壓力舒適度標準,以京滬線隧道為背景,研究了中國某型號標準動車組的單節車廂動態當量泄漏面積氣密閾值,得出以下結論: (1) 通過與試驗數據對比,說明本文所建立的“當量泄漏面積法”計算車內壓力的合理性及程序的準確性。 (2) 單列16編組動組以350 km/h的速度通過隧道長度大于500 m隧道時,當量泄漏面積閾值的最小值按符合500 Pa/s、800 Pa/3 s和1 000 Pa/10 s標準依次減小。 (3) 單列8編組和16編組動車組以380 km/h的速度過通過隧道長度大于500 m隧道時,在滿足800 Pa/3 s和1 000 Pa/10 s壓力舒適性條件下,16編組的當量泄漏面積閾值的最小值比8編組的小。 (4) 16編組動車組以不同速度通過隧道長度大于500 m隧道時,當量泄漏面積閾值的最小值隨著車速的增加而減小。 (5) 16編組動車組以中央等速交會的方式通過隧道長度大于900 m隧道時當量泄漏面積閾值的最小值比單列車通過時的小。 (6) 動車組車速400 km/h,符合1 000 Pa/10 s舒適性標時頭/尾車和中間車當量泄漏面積最嚴格分別為10.3 cm2和18.9 cm2。1.4 統計不同時間間隔內最大壓力變化量方法
1.5 車廂當量泄漏面積閾值確定方法
1.6 驗 證
2 計算結果及分析
2.1 計算參數及舒適性標準
2.2 車內外壓力波形成機理
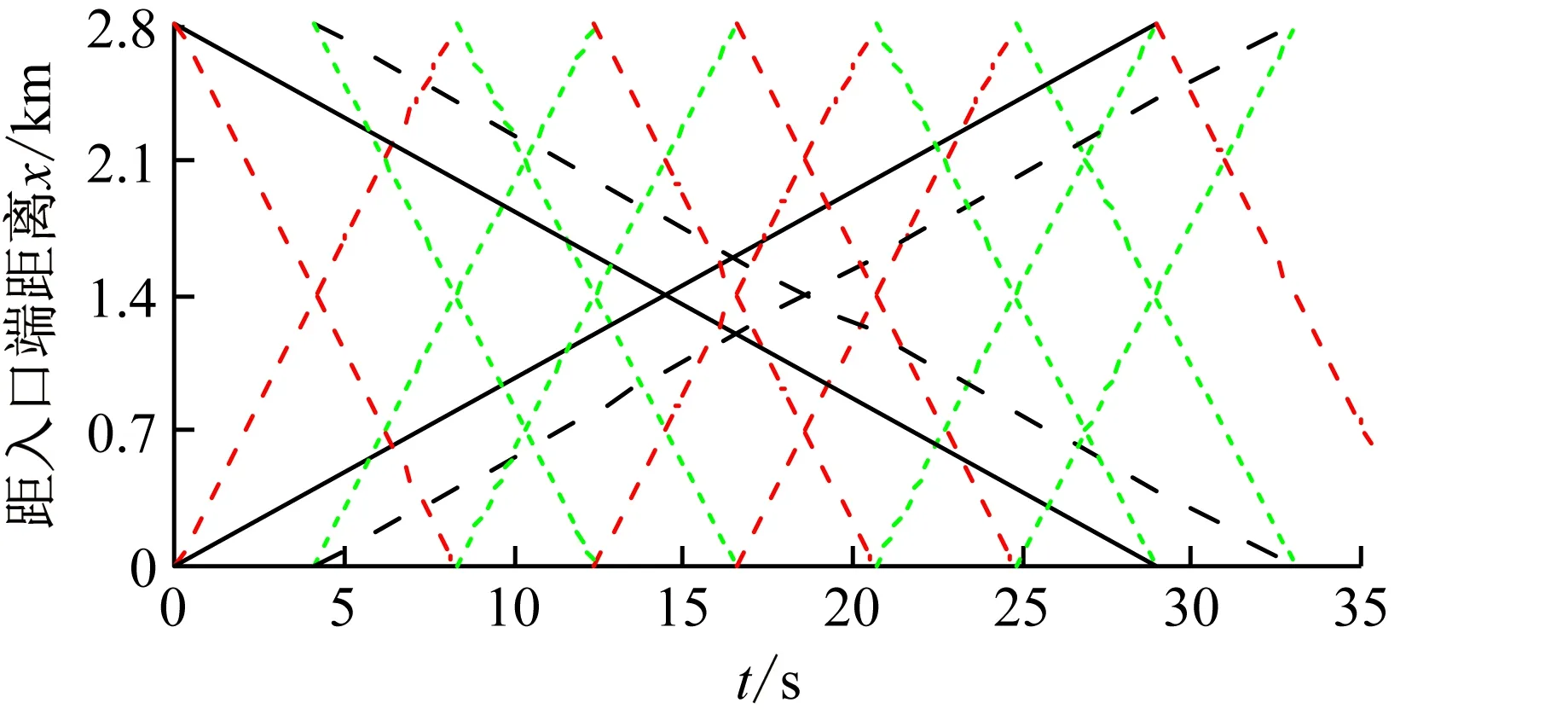
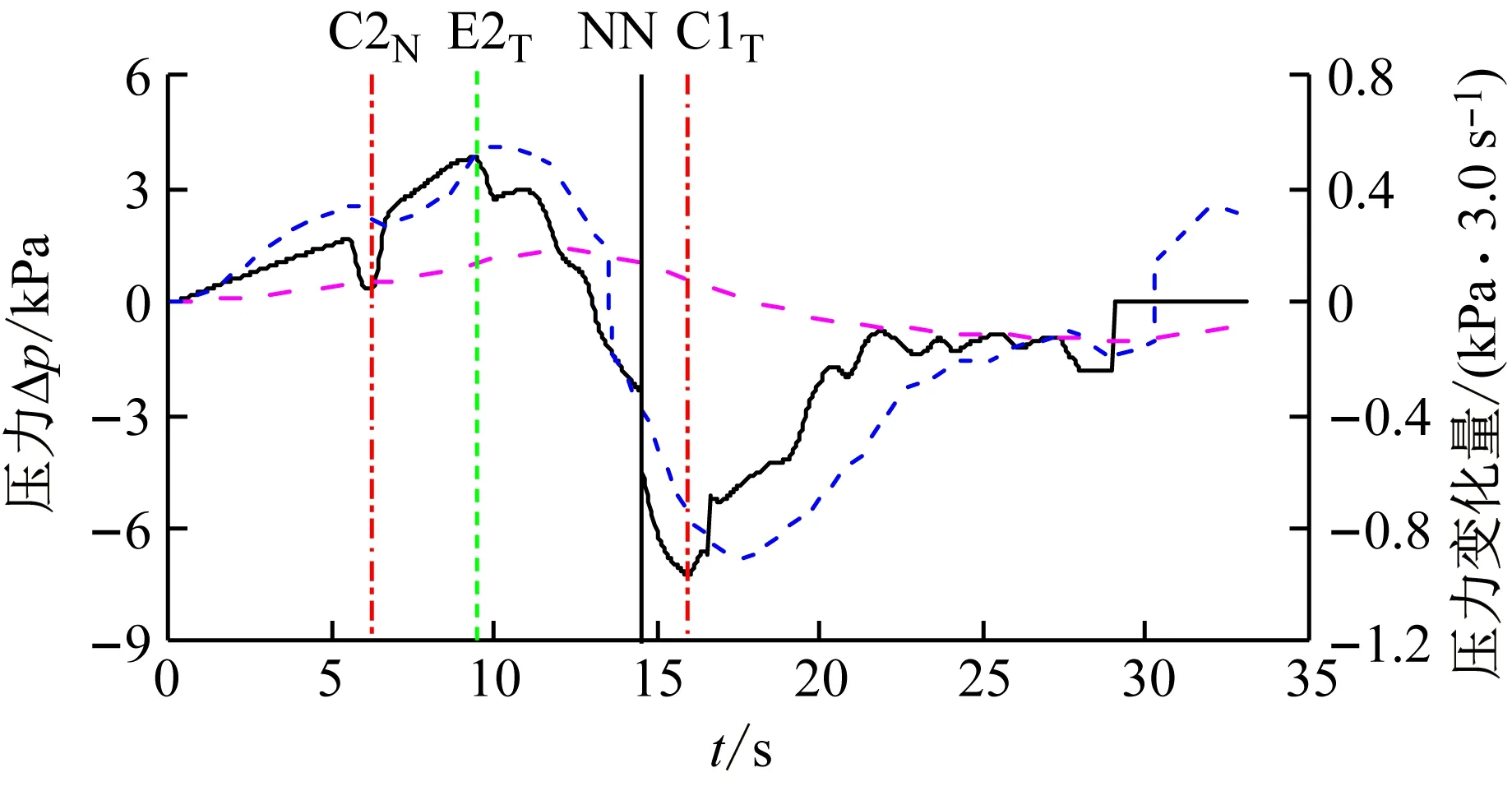
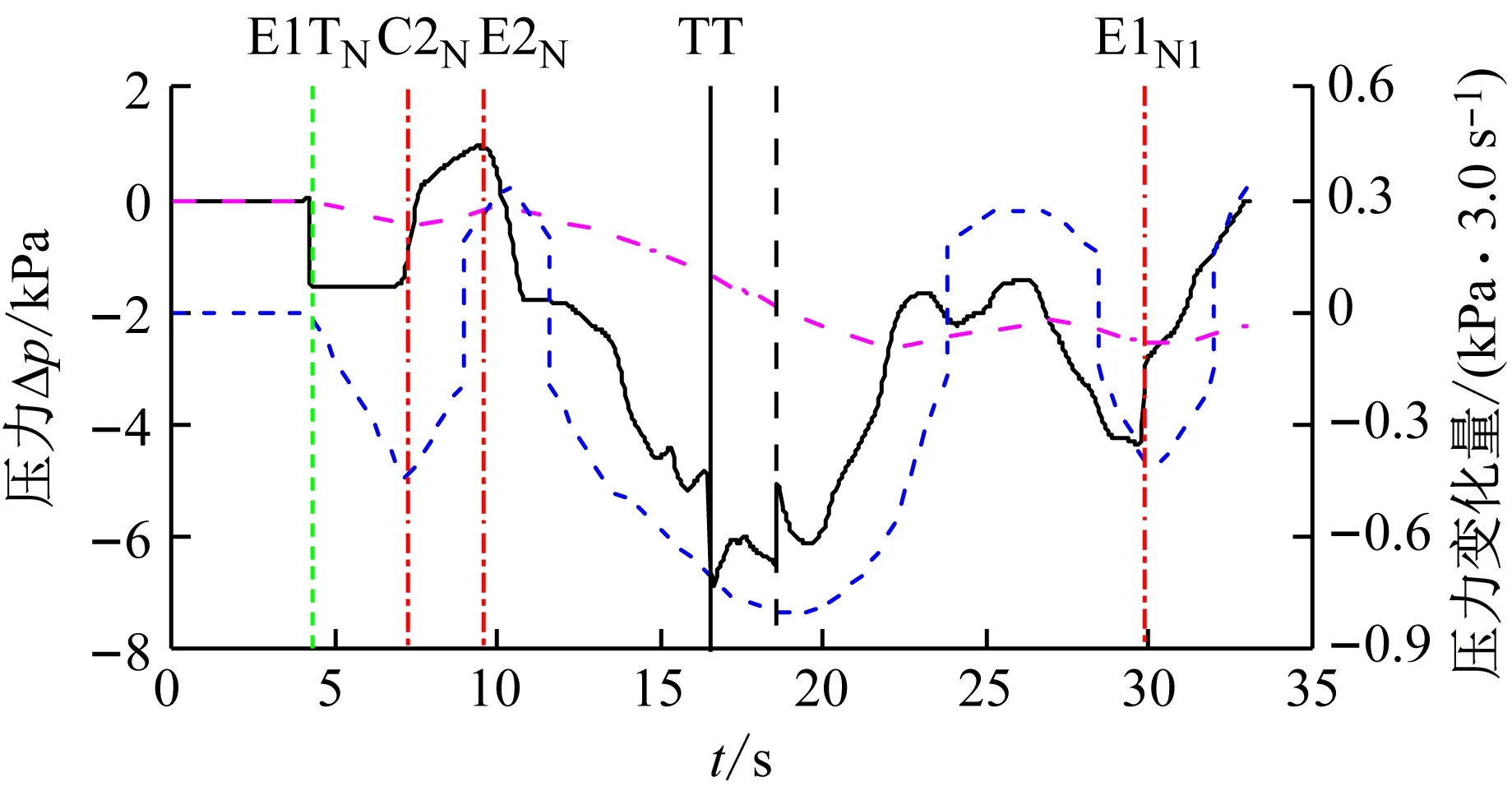
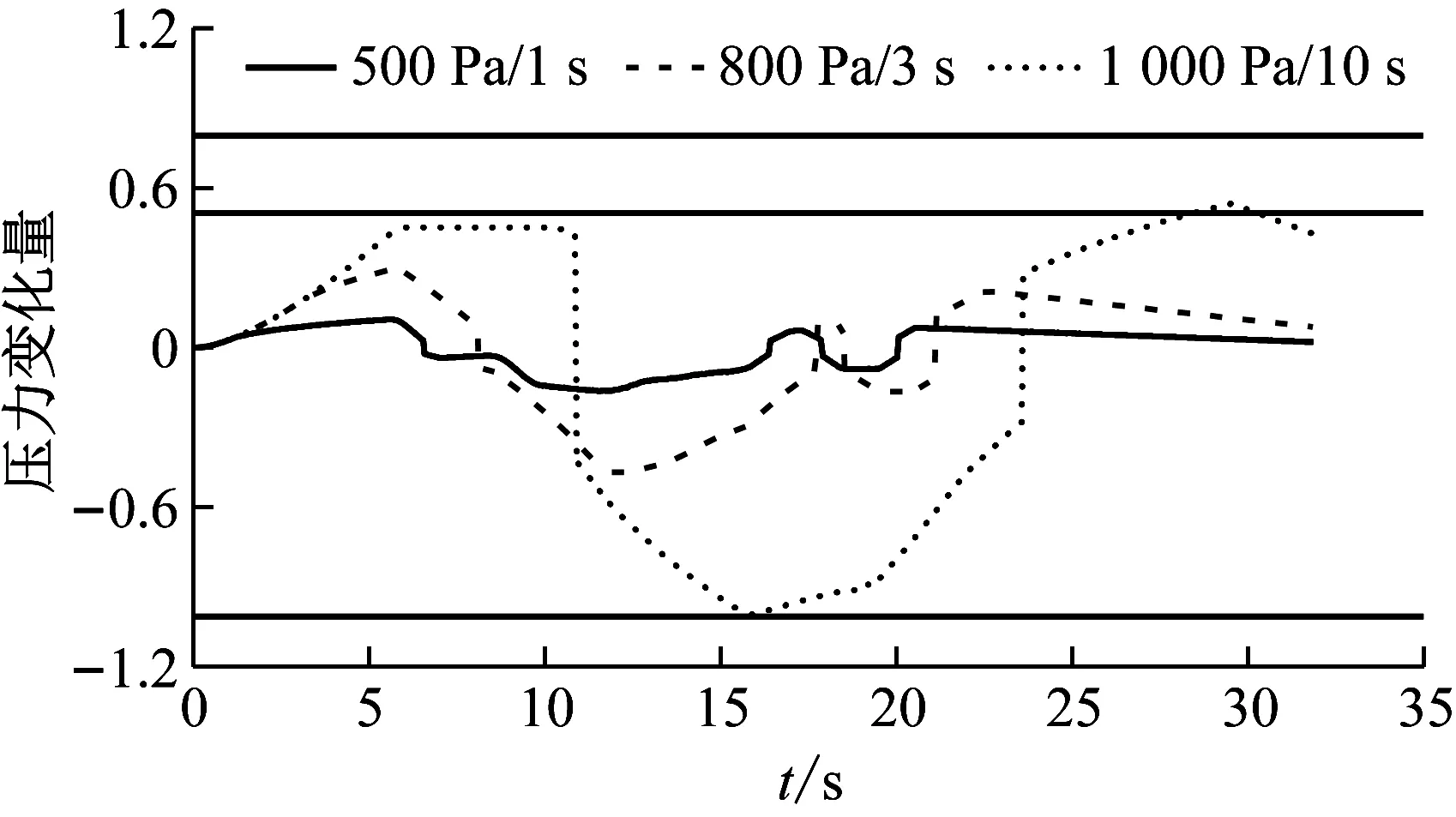
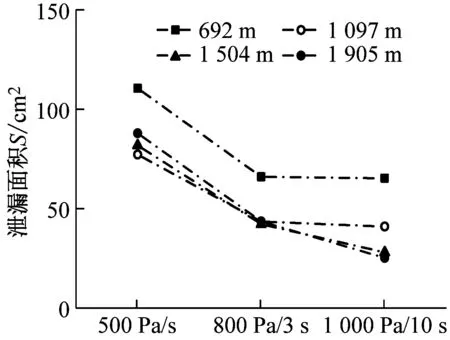
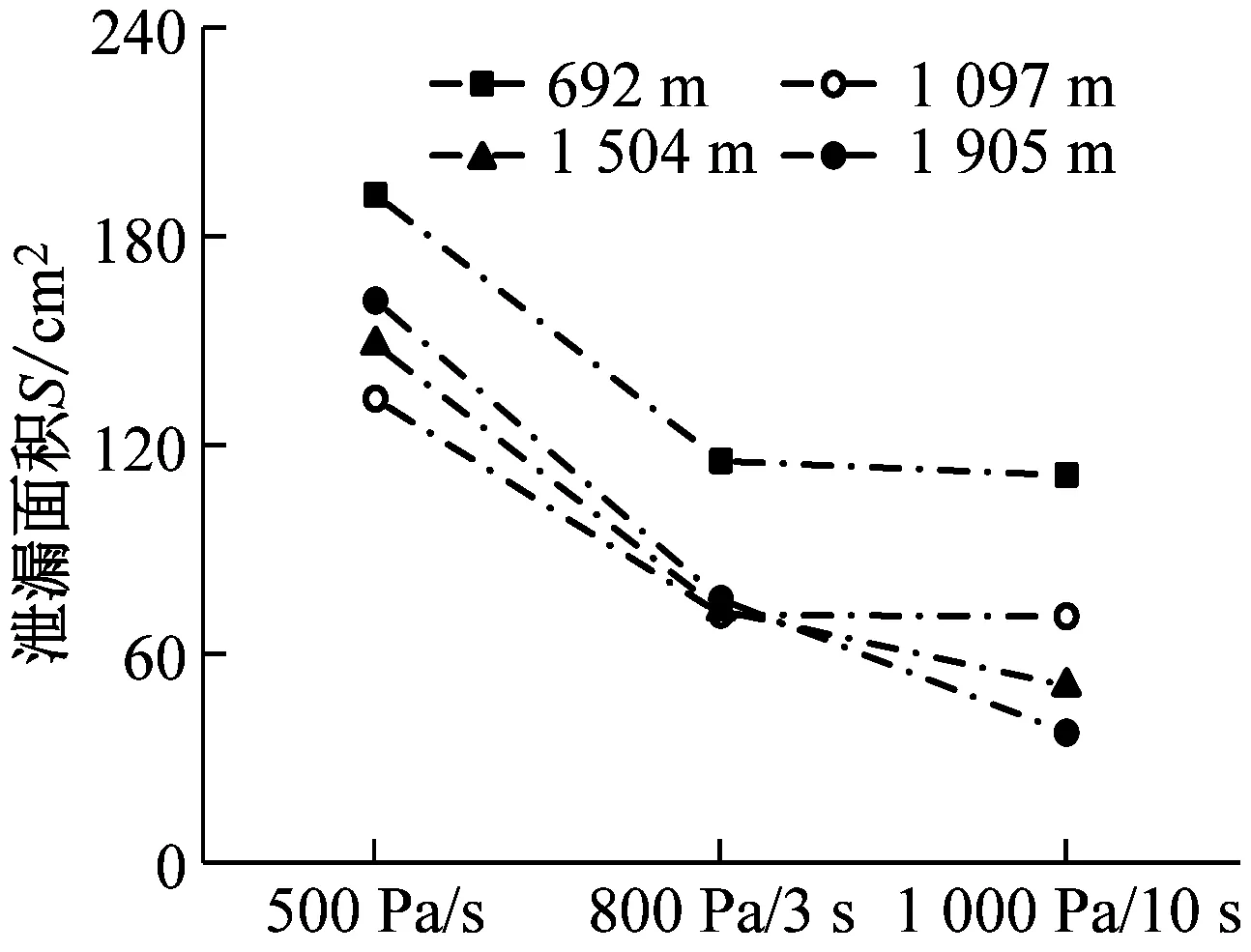
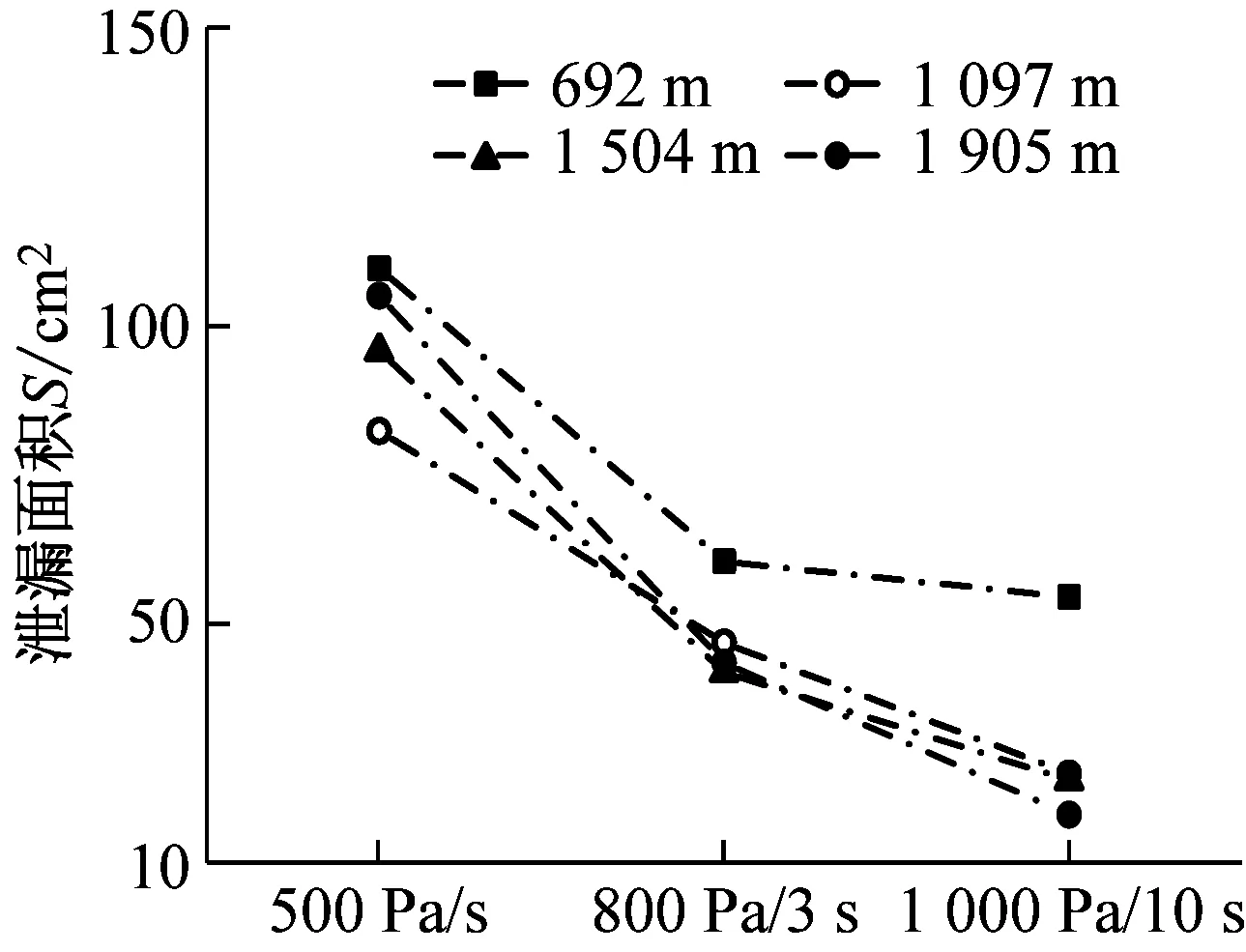
2.3 舒適性標準的影響特性
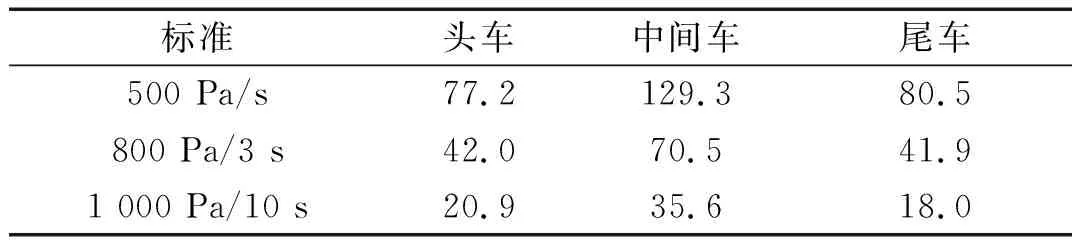
2.4 編組長度的影響特性
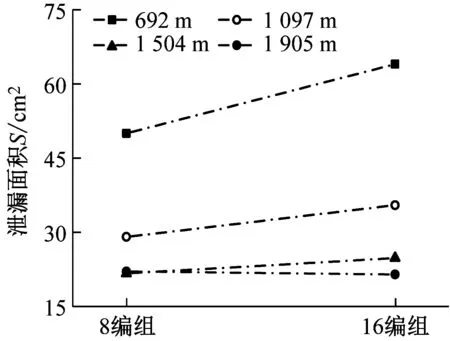

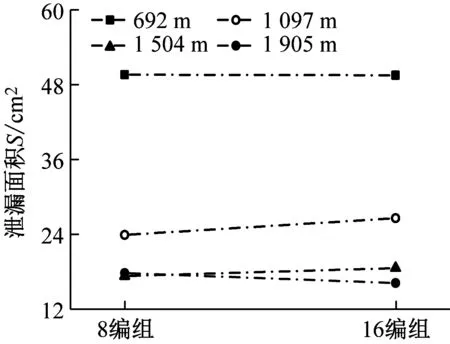
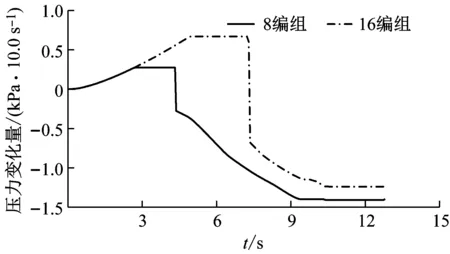

2.5 速度的影響特性

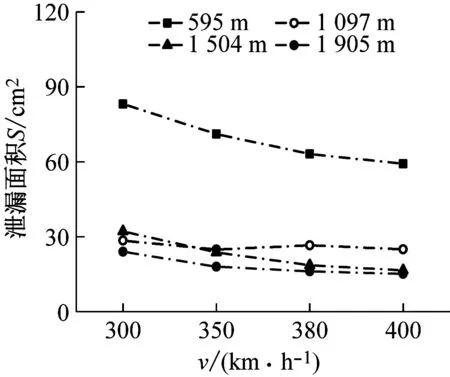
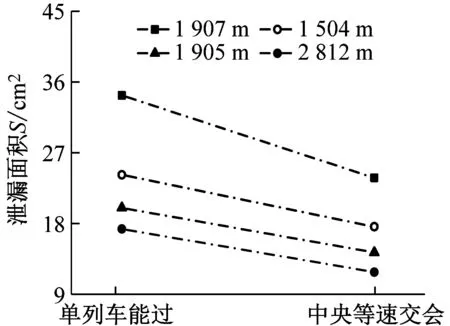
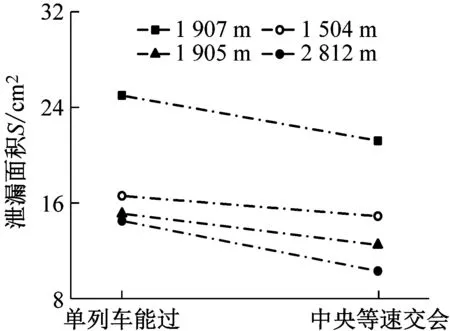
2.6 單列車過隧道與兩列車隧道交會對比



3 結 論

