大跨獨塔公軌兩用混合梁斜拉橋?qū)嵱谜{(diào)索方法*

全 偉，溫 欣，王東升

(1.沈陽建筑大學(xué) 交通工程學(xué)院，沈陽 110168；2. 黃山學(xué)院 建筑工程學(xué)院，安徽 黃山 245041；3. 河北工業(yè)大學(xué) 土木與交通學(xué)院，天津 300401)

大跨度斜拉橋的調(diào)索，包括理想成橋狀態(tài)和施工階段索力的確定，需要較多的工程實踐經(jīng)驗和較高的理論水平[1].目前的通用結(jié)構(gòu)計算程序，往往缺少相應(yīng)的調(diào)索模塊，使用起來也有很多的局限性.設(shè)計人員在斜拉橋設(shè)計時，需要豐富的調(diào)索經(jīng)驗，否則很難得到合理的索力[2-3].

針對斜拉橋調(diào)索，研究人員提出了各種不同的方法.吳霄等[4]給出了索力優(yōu)化的遺傳算法；陳志軍等[5]給出了基于粒子群算法的獨塔斜拉橋成橋索力優(yōu)化方法；苑仁安等[6]以及李國平等[7]針對斜拉索索力調(diào)整的無應(yīng)力狀態(tài)法進行了研究.以上研究方法均需要設(shè)計者具有較高的理論水平.本文結(jié)合佛山南海東平大道大橋的設(shè)計，針對大跨獨塔公軌兩用混合梁斜拉橋，提出實用簡單的調(diào)索方法：理想成橋狀態(tài)采用經(jīng)驗試算法；施工階段采用兩階段調(diào)索方法.實用調(diào)索方法原理簡單，容易掌握，調(diào)索快，主梁和主塔受力合理，達到了較好的效果.

1 工程介紹

圖1 東平橋橋型布置Fig.1 Layout of Dongping Bridge

2 理想成橋索力確定

2.1 調(diào)索目標(biāo)

斜拉橋成橋后，其內(nèi)力狀態(tài)和線形狀態(tài)均應(yīng)滿足設(shè)計要求.通過施工過程設(shè)置預(yù)拱度，斜拉橋線形可以不斷調(diào)整，以滿足成橋的線形.因此，重點在于合理控制斜拉橋的成橋內(nèi)力，使得結(jié)構(gòu)受力滿足要求.調(diào)索時應(yīng)滿足“塔直梁平”的基本準(zhǔn)則.針對獨塔公軌兩用混合梁斜拉橋的受力特點，制定了相應(yīng)的調(diào)索目標(biāo).

1) 橋塔.橋塔為壓彎構(gòu)件，由于軸向力的預(yù)加力效應(yīng)，可承受較大的彎矩.調(diào)索時，應(yīng)使恒載作用下兩側(cè)彎矩基本平衡.根據(jù)公軌兩用斜拉橋活載占比相對較大的受力特點，考慮運營之后汽車和軌道交通荷載的共同作用，可借鑒主梁預(yù)拱度的原理，塔身向岸側(cè)偏移，在一半活載效應(yīng)的作用下，塔身基本保持豎直.

圖2 橋塔構(gòu)造Fig.2 Structure of pylon

4) 錨墩和輔助墩.錨墩和輔助墩支座不出現(xiàn)負(fù)反力，或者通過壓重即可消除負(fù)反力.這樣就可以避免設(shè)置構(gòu)造復(fù)雜，造價昂貴且容易產(chǎn)生疲勞問題的拉力支座.

2.2 索力求解方法

理想成橋索力的確定一般不用考慮施工階段的影響，合理成橋狀態(tài)確定后，可以通過某種施工方案或者施工工序的調(diào)整，實現(xiàn)給定的合理成橋狀態(tài).理想成橋索力求解時，初始索力的擬定非常關(guān)鍵.良好的初始索力值對后期調(diào)索可起到事半功倍的效果.類似于剛性支承連續(xù)梁法的求解原理，針對佛山南海東平水道混合梁斜拉橋，采用索力豎向分量平衡梁重，并乘以放大系數(shù)的經(jīng)驗試算法確定初始索力，該方法原理簡單，通過幾次試算即可滿足要求，具體步驟如下：

1) 算出中跨混合梁鋼梁部分各個梁段的重量，然后使相應(yīng)斜拉索的豎向分量等于梁段重量，通過角度轉(zhuǎn)換得到中跨側(cè)索力，邊跨索力通過與中跨索力水平分量相等求得.初始索力的擬定如圖3所示.

圖3 初始索力擬定Fig.3 Determination of initial cable force

忽略主梁抗彎剛度的影響，令Wsi為第i根索所支承的恒載重量，根據(jù)豎向力的平衡，可得

Tsi=Wsi/sinαi

(1)

中跨側(cè)斜拉索引起的水平力為

Fsi=Tsicosαi=Wsi/tanαi

(2)

忽略橋塔抗彎剛度的影響，則主邊跨索力的水平分量應(yīng)相等，于是可求得邊跨側(cè)斜拉索初始索力，即

(3)

2) 上述初始索力計算中，未考慮活載的影響，根據(jù)活載所占結(jié)構(gòu)總荷載的比例，對所求索力乘以一個放大系數(shù)，輸入結(jié)構(gòu)中進行計算.之后對局部拉索索力進行微調(diào)，調(diào)整原則是短索索力小，長索索力大，呈遞增趨勢，索力均勻以及主塔彎矩小等，就可得到較理想的成橋索力.

采用上述方法計算時，應(yīng)注意橋塔在恒載作用下應(yīng)向邊跨側(cè)有一定偏移.具體調(diào)索時，可通過對邊、中跨調(diào)整放大系數(shù)來實現(xiàn).該方法原理簡單，操作方便，便于設(shè)計人員掌握.

3 施工階段索力確定

大跨獨塔混合梁斜拉橋施工時，斜拉索的張拉可采用一次張拉法或者多次張拉法.采用一次張拉法成橋后不再對拉索進行張拉，張拉次數(shù)少.但是施工過程索力需照顧到成橋索力的大小，該方法可能會造成斜拉橋施工過程中結(jié)構(gòu)內(nèi)力過大，對于二期恒載較大的斜拉橋，一次張拉法可能無法得到合理的成橋狀態(tài).

斜拉橋施工過程中，由于存在施工誤差等因素，為了使斜拉橋受力達到理想狀態(tài)，一般均會在成橋后進行一次調(diào)索.綜合以上因素，斜拉索張拉建議采用二階段調(diào)索法，其主要步驟如下：

1) 懸臂拼裝階段索力只是為了達到施工過程中的受力要求.因此，該索力主要用于平衡當(dāng)前施工階段的主梁自重以及施工過程中的荷載等.

2) 在成橋后對拉索進行二次調(diào)索，調(diào)索采用影響矩陣法[8-10]，通過迭代計算使其達到理想成橋狀態(tài)的要求.

采用二階段調(diào)索法，懸臂拼裝階段斜拉索初始拉力的確定只需滿足施工過程中的安全性，保證主梁基本平直，重點在于第二次調(diào)索，通過成橋后第二次調(diào)索擬合合理的成橋狀態(tài).

3.1 索力優(yōu)化方法

假定斜拉橋受力處于線彈性狀態(tài)，則可建立如下線性方程組，即

AΔT=ΔR

(4)

式中：ΔT為索力調(diào)整量；ΔR為控制目標(biāo)與理想成橋狀態(tài)控制目標(biāo)的差值；A為索力調(diào)整對控制目標(biāo)的影響矩陣.

在式(4)控制目標(biāo)中應(yīng)加入各種可能引起控制作用的物理量，使得該方程組的方程個數(shù)大大超過調(diào)整索力數(shù)，從而成為一個矛盾方程組，可求其廣義解(即最小二乘解).其原理為求ΔT，使得

(5)

為最小.式中，m、n分別為ΔT和ΔR的元素個數(shù).根據(jù)極值原理，為了使得式(5)最小，則有

ATAΔT=ATΔR

(6)

根據(jù)上述計算公式，針對第二階段的調(diào)索，利用影響矩陣法編制了基于MATLAB的斜拉橋調(diào)索程序，可方便得到擬合合理成橋狀態(tài)的第二階段拉索索力.影響矩陣可以采用大型有限元程序MIDAS直接求取.

3.2 控制目標(biāo)和加權(quán)矩陣的選取

在結(jié)構(gòu)布置確定的情況下，斜拉橋成橋合理狀態(tài)僅與恒載分布、索力及支座反力(成橋狀態(tài)三要素)有關(guān)，與結(jié)構(gòu)剛度分布、結(jié)構(gòu)非線性、施工過程無關(guān).該定理可以從力的平衡條件推出，任何結(jié)構(gòu)布置和恒載分布給定的斜拉橋，只要索力和支座反力已知，結(jié)構(gòu)就成為靜定體系，斜拉橋的內(nèi)力狀態(tài)可由索力和支座反力唯一確定.

因此，控制目標(biāo)ΔR可以取各對斜拉索索力以及各個支承處反力的差值.只要上述控制指標(biāo)接近目標(biāo)值，則施工后成橋索力即接近于理想成橋索力.本橋斜拉索共52對，因此，索力調(diào)整向量ΔT為52×1的向量，ΔR取斜拉索索力加上各個支承處豎向反力，因此其為59×1的向量.

由于不同的控制量量綱、數(shù)值大小或者重要程度不同，在式(4)中引入正定對角加權(quán)矩陣ρ，則該方程變?yōu)?/p>

ρAΔT=ρΔR

(7)

求取式(7)的最小二乘解，可以得到

ATρ2AΔT=ATρ2ΔR

(8)

加權(quán)矩陣ρ的取值，可以根據(jù)其量綱和控制量的重要程度靈活選取，得到更優(yōu)值.通過設(shè)置加權(quán)系數(shù)，可有效提高式(6)的求解速度和精度.

4 東平水道大橋調(diào)索結(jié)果

圖4 東平橋有限元模型Fig.4 Finite element model for Dongping Bridge

4.1 理想成橋索力

采用經(jīng)驗試算法進行理想成橋索力的求解.試算時調(diào)整橋塔兩側(cè)索力的比例系數(shù)，使得橋塔在恒載作用下人為往邊跨側(cè)產(chǎn)生一定程度的偏移.一般可參考常規(guī)主梁預(yù)拱度的設(shè)置方法，使得在1/2活載作用下，主塔基本保持豎直.

1) 主塔.恒載作用下，主塔塔頂往邊跨側(cè)偏移61 mm，活載滿載后，橋塔向中跨偏移67 mm，橋塔塔身受力合理，基本處于全截面受壓狀態(tài).

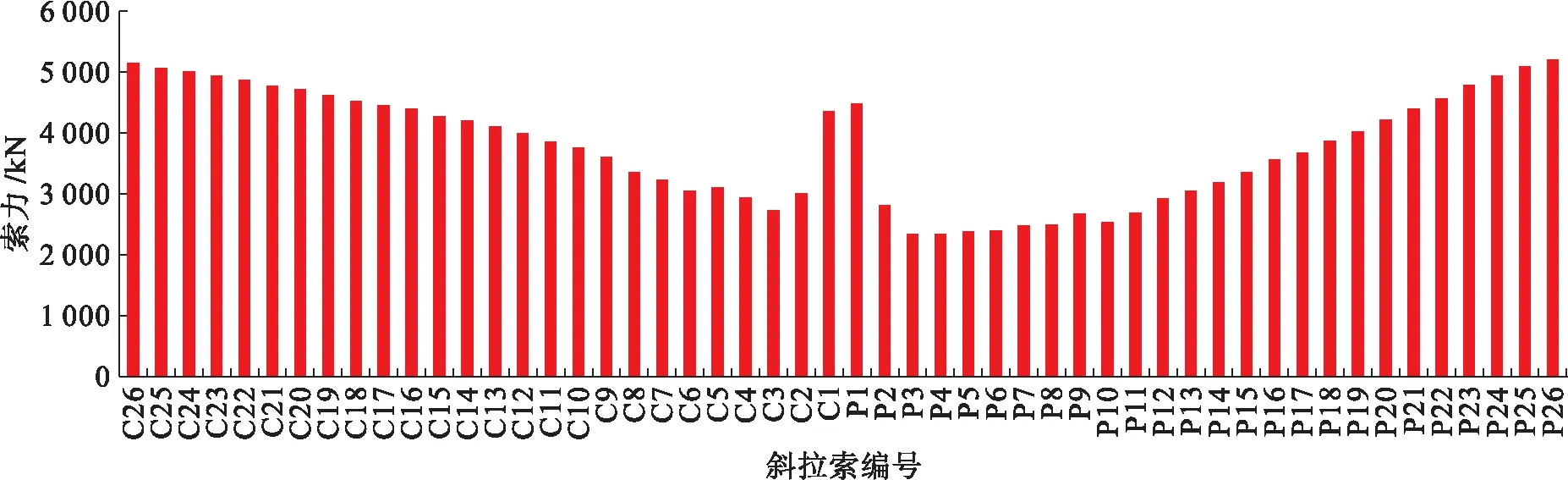
圖5 理想成橋狀態(tài)下斜拉索索力Fig.5 Cable forces under ideally completed state

3) 主梁.主梁受力合理，恒載作用下，主跨鋼梁側(cè)向上預(yù)留一部分負(fù)彎矩，如圖6所示(單位：kN·m).主力+附加力荷載組合下，鋼梁彎矩包絡(luò)圖正負(fù)彎矩值分布均勻，受力合理，如圖7所示(單位：kN·m).

圖6 成橋狀態(tài)彎矩圖Fig.6 Bending moment diagram under completed bridge state

圖7 主+附彎矩包絡(luò)圖Fig.7 Envelope diagram of bending moment under main and additional force

通過向上預(yù)留負(fù)彎矩，使得主梁在主力+附加力組合下，正負(fù)彎矩幅值相近，滿足了主梁受力的要求.混凝土梁由于在邊跨側(cè)設(shè)置了兩個輔助墩，跨徑較小，且由于斜拉索多點彈性支承和預(yù)壓作用，改善了主梁受力，通過配置適當(dāng)?shù)念A(yù)應(yīng)力鋼束即可滿足要求.

4) 錨墩、輔助墩支反力.表1給出了P2墩(前伸跨中墩)墩頂部設(shè)置壓重后計算結(jié)果.如未設(shè)置壓重，雖然P2墩頂支座均未出現(xiàn)負(fù)反力，但最小豎向力僅為361 kN，富裕量較小，考慮到后期超載的可能性等其他不確定性因素，設(shè)計時在P2墩頂適當(dāng)設(shè)置一定的壓重.設(shè)置壓重長度為28 m，荷載集度為260 kN/m，總壓重為7 280 kN.

表1 各墩(塔)支承處豎向反力Tab.1 Vertical reaction force at each pier (pylon) support kN

4.2 施工階段索力

根據(jù)施工階段索力確定的二階段調(diào)索法原理，首先求得懸臂拼裝階段的索力.該階段索力的確定方法類似于理想成橋狀態(tài)下索力的確定方法，確定的原則是拉索索力的豎向分量平衡斜拉橋梁段的重量.第一次和第二次拉索張拉力如圖8所示.

圖8 第一次和第二次拉索張拉力Fig.8 First and second cable tension force

斜拉橋成橋合龍上二期恒載之后，一般最好不再調(diào)整索力.如果調(diào)整將在橋面鋪裝層中產(chǎn)生附加內(nèi)力.因此，橋梁合龍未上二期恒載之前，對全部斜拉索進行第二次張拉.影響矩陣A采用MIDAS程序求解，對各根斜拉索施加單位索力(一般取100 kN)，求取施加單位索力時，各根斜拉索索力的變化值以及各個支承處的支承反力值.本橋影響矩陣A的維數(shù)為59×52.加權(quán)矩陣ρ反應(yīng)了結(jié)構(gòu)控制量的量綱和重要程度，其維數(shù)為59×59，矩陣對角線上的數(shù)值可根據(jù)索力和支反力的量綱和重要程度進行試算.

通過優(yōu)化求解后，重新模擬施工計算求得成橋內(nèi)力，與確定的理想成橋狀態(tài)對比，可通過修改這些控制參數(shù)的目標(biāo)值或調(diào)整加權(quán)系數(shù)，將兩者的不閉合程度降到最低.值得注意的是，結(jié)構(gòu)最終形成的內(nèi)力與其施工順序有密切的關(guān)系，理想成橋狀態(tài)只是作為一個理想目標(biāo)值.通過迭代計算后，其最終成橋狀態(tài)只能接近于理想成橋狀態(tài).最終提交設(shè)計文件的成橋索力等參數(shù)應(yīng)該是考慮施工階段后的成橋索力.

通過計算，最終成橋索力以及理想成橋索力的對比如圖9所示，兩者相差最大不超過1.9%.最終成橋階段，斜拉橋各個構(gòu)件的內(nèi)力和變形情況均很好地滿足了設(shè)計要求.

圖9 實際成橋和理想成橋索力對比Fig.9 Comparison of cable force between actually and ideally completed bridges

5 結(jié) 論

針對斜拉橋調(diào)索需要較高的理論水平，設(shè)計者較難掌握的現(xiàn)實，結(jié)合佛山南海東平水道大橋的調(diào)索，給出了確定其理想成橋索力和施工階段索力的方法.目前，該斜拉橋已經(jīng)順利合龍，主梁主塔受力合理，調(diào)索取得了較好的效果.實用調(diào)索方法具有較好的推廣應(yīng)用價值.針對大跨獨塔混合梁斜拉橋的調(diào)索，得出以下結(jié)論：

1) 公軌兩用混合梁斜拉橋調(diào)索時，應(yīng)合理制定成橋目標(biāo)：考慮到公軌兩用斜拉橋活載較大，應(yīng)使橋塔成橋狀態(tài)預(yù)先向邊跨側(cè)偏移，這樣活載作用后，橋塔受力更合理；對于主梁，同樣應(yīng)預(yù)留一些負(fù)彎矩，使得考慮活載后，主梁受力更均衡.

2) 理想成橋狀態(tài)采用索力豎向分量平衡梁重，并乘以放大系數(shù)的方法試算確定合理成橋索力，計算簡單，容易掌握.

3) 施工階段索力推薦采用二階段調(diào)索方法：第一階段僅需滿足施工階段受力需求，平衡相應(yīng)梁段重量和施工階段荷載即可；第二階段在主梁合龍上二期前采用影響矩陣法對所有斜拉索進行二次調(diào)索.其中，影響矩陣可以通過MIDAS有限元程序求得，并采用基于MATLAB語言編制的影響矩陣法程序求取二次調(diào)索索力.該方法簡單實用，容易掌握，調(diào)索速度快，很好地滿足了設(shè)計要求.