工況對管道凹陷形成及管道安全性的影響

（廣東省特種設備檢測研究院，廣東佛山 528251）

管道運輸有安全可靠、量大、連續迅速及成本低等優點，油氣管道已經成為國內外能源運輸的動脈。管道失效事故會造成巨大的經濟損失，研究其失效形式具有重要意義［1-3］。凹陷是管道橫截面上的永久塑性變形，其存在會增大管道的局部應力，往往是管道發生疲勞和應力腐蝕裂紋的發起點［4-5］，成為管道失效的重要原因之一。國內外學者針對凹陷管道做了大量研究工作。Dawson S J等［6］通過數據統計發現，歐洲多數管道存在大量的凹陷。焦中良等［7］針對國內某條管道進行凹陷統計，發現平均每公里存在1.6處凹陷 。有嚴重凹陷的管道，在一定內壓作用下可能破裂或萌生裂紋，影響管道正常安全運行。Rosenfeld M［8］通過試驗發現，不同形狀的凹陷引起失效點的位置是不同的。Yi Shuai等［9］通過對凹陷管道的爆破試驗發現，越靠近凹陷中心，應變隨管道內壓增加變化越明顯，當管內壓力達到管壁屈服壓力后凹陷邊緣附近沿軸向有反凸現象。鐘功祥等［10］對不同支撐角度下凹陷進行的有限元模擬及應變分析表明，支撐方式為45°對稱分布時等效應變最小。Jie Cai等［11］通過有限元模擬和試驗研究擬合了純彎矩下含凹陷管道的剩余極限強度計算公式。Ramezani M等［12］通過模擬得出了應變隨凹陷深度和管道內壓的變化規律。Jan Kec等［13］通過壓力試驗觀察凹陷的輪廓變化，測量應力應變的變化。帥健、帥義、楊瓊等［14-16］通過爆破試驗發現，內壓的波動會使凹陷所在管道位置產生較大的應力和應變，提出了一種凹陷管道工程的簡易評價方法。馬欣等［17-18］通過有限元模擬建立了凹陷模型，分析了凹陷參數以及內壓對管道軸向應變以及韌性失效的影響，針對內腐蝕凹陷研究了凹陷等效應變在復合缺陷下的變化規律。陳健等［19］基于有限元法研究得出凹陷深度、壁厚以及擠壓體的尺寸對凹陷等效應變的影響，該結論對凹陷評價以及風險排序有一定指導作用。李成兵等［20］給出了無凹角和有凹角這2種凹陷的判別方法，指出無凹角凹陷對管道安全影響較大。這些研究以凹陷管道為對象，未考慮凹陷形成時間段對管道的影響，文中對此展開研究。

1 管道建模及凹陷形成有限元模擬

1.1 管材屬性數據來源

X70管道材料彈性模量為210 GPa，屈服強度為 485 MPa，泊松比為0.3，抗拉強度為 675 MPa。為了使有限元分析結果更準確，進行X70管道的拉伸試驗時，以實測的應力和應變數據（圖1）作為模擬對象的輸入數據。

圖1 X70材料實測應力-應變曲線

1.2 管道模型及凹陷的形成

X70管道模型的公稱直徑為914 mm，壁厚為12 mm，長度以可避免凹陷部位的應力影響區與管道端面相互作用并且不影響計算準確性為合適，一般長徑比不小于3。采用剛性壓頭對管道進行加壓成型，模擬管道外壁與硬物擠壓或碰撞形成凹陷的過程，將此過程劃分為接觸建立、外載荷加載及外載荷卸載3個階段（圖2）。選擇三維實體單元SOLID185進行網格劃分，對壓頭與管道接觸的地方進行網格加密，選擇Target170單元和Conta174單元進行接觸對的建立。

圖2 管道模型、網格劃分及凹陷形成過程

1.3 凹陷加載及工況設置

基于管道內壓會使管道上已經形成的凹陷產生一定回彈的事實，認為內壓、外載荷的加載、卸載順序將改變凹陷的最終形態及其對管道的影響。

按照內壓、外載荷在管道上作用的先后順序將凹陷的形成分為3種工況。工況1，首先對管道施加內壓，再用剛性壓頭進行凹陷成型（即凹陷加載），最后去掉壓頭擠壓作用（即凹陷卸載）。工況2，首先進行凹陷加載，再進行凹陷卸載，最后施加管道內壓。工況3，首先進行凹陷加載，再施加管道內壓，最后進行凹陷卸載。

2 各工況下凹陷對管道影響對比分析

2.1 管道應力

考慮到凹陷加載過程較為復雜，而且帶高壓實施沖壓凹陷操作危險性高，故以數值模擬代替試驗。在建立管道有限元模型的基礎上，利用ANSYS軟件分別模擬3種工況下凹陷形成的過程，采用半徑100 mm的剛性壓頭，在管道上成型出深度為10 mm的凹陷，管道內壓為10 MPa。3種工況下管道的應力分析結果見圖3～圖5。

圖3 工況1下管道等效應力分布云圖

圖4 工況2下管道等效應力分布云圖

圖5 工況3下管道等效應力分布云圖

從圖3可以看到，工況1下管道沒有凹陷缺陷存在時，10 MPa內壓下管段最大等效應力為340.929 MPa。當管道與壓頭擠壓形成凹陷時，管道最大等效應力為485.678 MPa。當壓頭卸載之后，管道凹陷處有一定回彈，應力有一定減小，但應力更加集中。

從圖4可以看出，工況2下凹陷加載時，管道的等效應力達到最大，為461.666 MPa。凹陷卸載后，管道存在一定的殘余應力。施加內壓后，凹陷部位進一步回彈，因此管道的最大等效應力僅為428.735 MPa。

從圖5可以看出，工況3下凹陷加載階段與工況2相同，但由于工況3是在凹陷沒有卸載情況下施加內壓，故導致管道等效應力較大，最大為532.531 MPa。當凹陷卸載后，在自身塑性與內壓的共同作用下，凹陷處迅速回彈，管道等效應力大幅度下降。

對比圖3、圖4和圖5可知，工況1和工況2下管道的最大等效應力發生在凹陷加載階段，而工況3發生在內壓加載階段。工況1下在凹陷卸載前后的等效應力均較大，工況3下在內壓加載階段的等效應力是各個工況 （包括每個階段的形成過程）的最大值。相對于工況1及工況3，工況2下管道的等效應力較小。

2.2 管道凹陷回彈

X70是一種高強度管線鋼，具有屈服強度高、回彈現象明顯的特點，因此研究凹陷的回彈具有一定意義［21］。

模擬3種工況下凹陷加載、凹陷卸載、施加內壓過程，得到的管道凹陷變形量分布云圖分別見圖 6～圖 8。

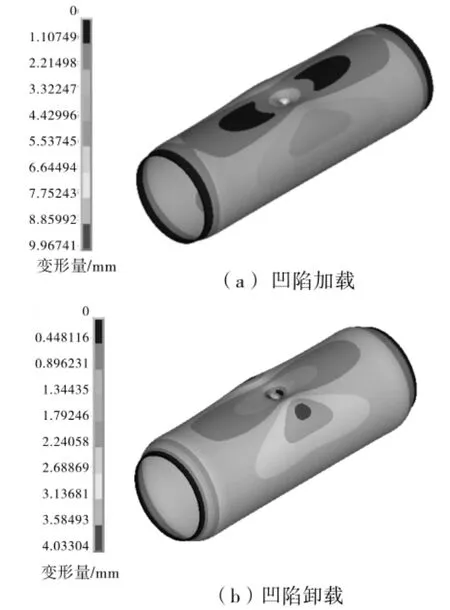
圖6 工況1下管道凹陷變形量分布云圖

從圖6可以看出，工況1下凹陷卸載后，凹陷有顯著回彈。采用壓頭擠壓形成1 mm深的凹陷，在卸載后的最大變形量只有4.03 mm。

由于工況2在凹陷加載時沒有內壓存在，因此存在2段的回彈過程。從圖7可以看出，在凹陷卸載后，凹陷附近的管壁存在一定的彈性變形恢復，最大變形量約為5.92 mm，在施加內壓后，管壁進一步發生反向的塑性變形，導致凹陷進一步回彈，最大變形量約為4.50 mm。

圖7 工況2下管道凹陷變形量分布云圖

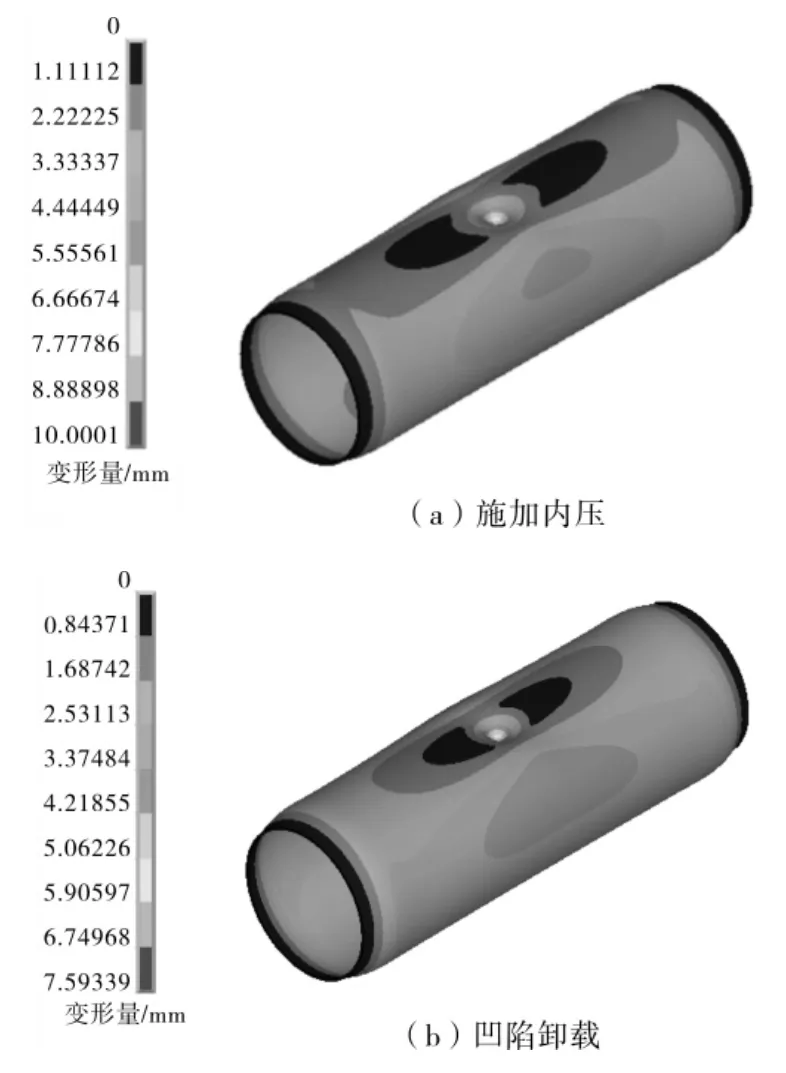
圖8 工況3下管道凹陷變形量分布云圖

從圖8可以看出，工況3下在施加內壓時凹陷沒有發生回彈，這是由于此時受剛性壓頭的外載荷作用，當凹陷卸載后只發生很小的回彈，最大變形量為7.59 mm。

對比圖6、圖7和圖8并進行計算，工況1下凹陷回彈最顯著，回彈系數為0.403。工況2下凹陷分2段回彈，施加內壓后的回彈系數為0.45。工況3下雖然在凹陷加載時沒有內壓存在，但施加內壓時由于受外載荷的作用，只有一段回彈且回彈程度較小，回彈系數為0.759。

2.3 管道極限承載能力

管道極限承載能力是指管道發生失效時的內壓大小［22］。當管壁的等效應力達到某一參考應力值時，管道發生失效破壞，凹陷、腐蝕、裂紋等缺陷的存在會極大程度降低管道的極限承載能力［23］。

保持壓頭半徑為100 mm不變，建立不同凹陷深度的管道有限元模型，通過模擬結果對比3種工況下形成的凹陷對管道極限承載能力的影響，結果見圖9。

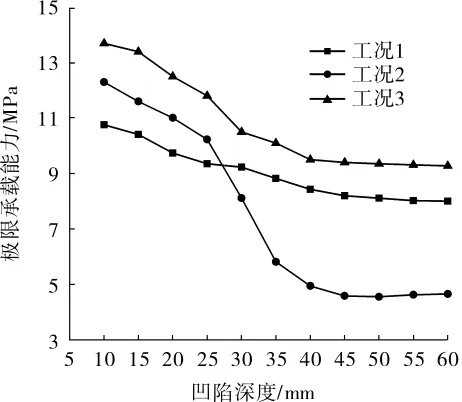
圖9 不同工況下管道極限承載能力隨凹陷深度變化曲線

從圖9看出，3種工況下管道極限承載能力均隨凹陷深度的增加而降低，當凹陷深度達到45 mm后，3種工況下的管道極限承載力均處于穩定。其中工況2下凹陷深度達到25 mm后，管道的極限承載能力迅速下降，且下降為3種工況中最低。

3 結語

將內壓和外載荷按照特定方式形成的組合定義為不同工況，以X70管道為對象，通過有限元建模和數值模擬研究了管道在3種特定工況下形成凹陷對管道安全性能的影響。3種工況下凹陷形成過程中的最大等效應力發生的階段不同，工況1與工況2下發生在凹陷加載階段，工況3下發生在內壓加載階段。3種工況下管道凹陷處均有一定回彈，工況下1下凹陷回彈最顯著，回彈系數為0.403，工況2和工況3下的回彈系數分別為0.45和0.759。3種工況下管道極限承載能力均隨凹陷深度的增加而降低，其中工況2下管道極限承載力受凹陷深度影響最嚴重，工況3下管道極限承載能力受凹陷深度影響最小。