遙感圖像的有向空間高斯混合模型分割方法

盧印舉，段明義，蘇玉

(鄭州工程技術學院 信息工程學院，鄭州 450044)

0 引言

圖像分割是數字圖像處理、計算機視覺領域中的基本問題之一，目前已取得了良好的應用成果，包括遙感圖像分析技術[1]、磁共振成像(magnetic resonance imaging，MRI)技術[2]、合成孔徑雷達(synthetic aperture radar，SAR)圖像技術[3]以及目標檢測技術[4]等應用領域。它主要是利用各類圖像所具有紋理、顏色以及灰度等各方面的特征來劃分圖像，使各個區域展現出某一類特性。但是，在實際成像處理時，由于一系列因素包括場偏移效應、局部容積效應以及噪音等的影響，導致所采集到的圖像出現了一些不同的特點，如復雜的場景分布、更為模糊的界線、比較低的對比度以及減低的特征易變性等，從而進一步降低了圖像分割精度。因此，圖像分割被認為是計算機視覺領域的核心探索問題。

到目前為止，有許多圖像分割方法及其改進形式。由于本文研究的是基于概率圖模型圖像分割方法，因此，僅對以概率統計作為基礎的圖像分割處理進行介紹與分析，主要有高斯混合模型(Gaussian mixture model，GMM)和馬爾科夫隨機場(Markov random field，MRF) 2種分割模型。

傳統的高斯混合模型[5]在進行圖像分割的過程中，只是利用了像素的灰度，但是并未對各個像素間所對應的空間信息給予充分的關注，所以圖像噪聲顯著地影響了圖像分割的最終結果，從而導致分割精度水平低下。針對干擾噪聲容易影響常規的高斯混合模型這一難點，文獻[6]在圖像預處理的基礎上，提出了一種基于圖像重塑的新型分割方法。該方法通過引入相似性度量因子，利用權值將鄰域像素值加權和的結果作為中心像素重塑后的具體像素值，進而分析重塑之后的有關圖像。

馬爾科夫隨機場理論[7]是以統計學相關模型為基礎，Geman等[8]在1984年提出并廣泛應用于圖像處理領域，標注有關的圖像像素從而達到圖像分割的目的。利用MRF與GRF的等價關系，吳一全等[9]闡明MRF的聯合分布是具有特殊形式的Gibbs分布。以馬爾科夫隨機場理論為基礎，許多面向圖像分割融合高斯混合模型或者聚類的方法也被相繼開發出來。Roula等[10]利用MRF參數對紋理進行了描述，從而提出基于紋理特征的高斯混合模型圖像分割技術。同時，科研人員對MRF分割算法做出了進一步的完善，提出了一系列改進的MRF分割模型算法[11]。典型的模型有快速馬爾可夫隨機場、融合其他分割算法的混合模型以及隱馬爾可夫隨機場。以圖像像素的灰度特征信息為主的學者們[12]將圖像的形狀特征信息和紋理特征信息引入到馬爾科夫隨機場中，利用不同的特征提取方法實現對圖像特征信息的提取，以各類圖像特征信息為基礎來改善圖像分割效果。

上述分割方法未對相鄰像素間所具有的內在關聯以及圖像空間的信息等因素給予充分的考慮，使得不能以連續的方式來合理地分割某些圖像，從而導致所得的結果中形成了數量眾多的噪點。本文提出了一種基于有向空間關系高斯混合模型的遙感圖像分割算法，主要貢獻為：1)設計了一個改進高斯混合模型，合并了像素之間的空間信息對高斯混合模型的先驗概率和后驗概率進行約束，以提高觀測數據場對圖像理解的敏感性并進行對應關系的評估和更新；2)引入馬爾科夫隨機場并和高斯混合模型相結合，通過能量函數中灰度信息的分量控制，解決傳統期望極大算法在M步驟無法最大化優化求解缺陷；3)定義的空間約束能夠確保圖像在進行空間更新時算法結構的穩定，通過交替進行評估像素與類別之間的對應關系和空間約束變換，實現圖像的精準分割。與當前流行的3種算法相比，本文所提出的遙感圖像分割算法展現出了卓越的分割性能。

1 模型建立

給定獲取到的遙感圖像X={xi}1≤i≤N，N是像素總數量，xi表示第i個像素的灰度值，同時將圖像分割為K個類別標簽，第j區域的統計參數用μj、∑j分別表示均值和方差矩陣。模型的參數描述為：

Θ={μj，∑j}1≤j≤K

(1)

圖像觀測數據對數似然函數是關于圖像分割參數的一個函數，描述為：

L(Θ|X)=logP(X；Θ)

(2)

由于缺失數據的存在，即像素xi所屬的混合高斯模型分量直接對式(2)進行最大化求解十分困難，因此，引入隱含變量Z={zi=j}1≤j≤K。zi=j表示將像素點xi分配給高斯混合模型的第j個高斯分量。(X，Z)構成了高斯混合模型的完整數據，以給定的圖像為觀測條件，在隱藏事件空間中將完整數據對數似然函數的數學期望替代式(2)所述的圖像對數似然函數，得到式(3)。

ε(Θ|X，Z)=EZ[log(P(X，Z；Θ)]

(3)

給定zi=j即xi屬于第j區域條件下，圖像像素xi的條件概率分布服從高斯分布，圖像像素xi的邊緣分布用式(4)表示。

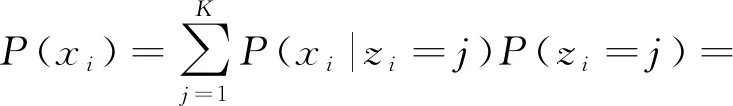
(4)

令πij=P(zi=j)(i=1，2，…，N，j=1，2，…，K)，遙感圖像分割模型的完整參數集合用式(5)表示。

Φ={μj，∑j，πij}(i=1，2，…，N，j=1，2，…，K)

(5)

取圖像完整數據對數似然期望最大化，利用式(4)～式(5),將式(3)改寫為式(6)。

ε(Φ|X，Z)=∑ZP(Z|X，Φ)logP(X，Z；Φ)

(6)

2 遙感圖像分割算法

2.1 遙感圖像像素的后驗概率

根據貝葉斯定理，計算給定圖像像素xi條件下zi=j的后驗概率αij=P(zi=j|xi)：

(7)

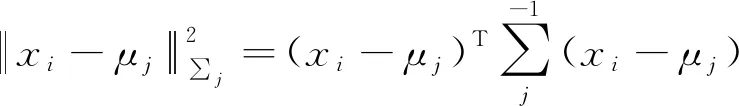
2.2 遙感圖像分割目標函數建模

將馬爾科夫隨機場模型的圖像空間信息以先驗概率[13]的方式引入到高斯混合模型，將式(7)代入式(6)并取負對數，得到遙感圖像分割的條件期望似然函數，用式(8)表示。

L(，

(8)

式中：β為馬爾科夫隨機場的溫度系數。

2.3 遙感圖像分割模型參數更新

根據最大后驗概率理論判斷圖像中每個像素的分類標簽，從而得到分割結果。對式(8)目標函數求偏導，?φ/?uj=0，?j∈[1…K]，得到式(9)。

(9)

令?φ/?∑j=0，?j∈[1…K]可以實現對∑j的估計，得到式(10)。

(10)

忽略式(8)中不依靠先驗的常數項,并利用拉格朗日乘數法，目標函數變為：

(11)

令偏導函數等于0，得到：

(12)

(13)

2.4 算法步驟描述

根據圖像分割的標簽類別數量，基于K均值算法選擇一個計算出的GMM參數的初始值，通過交替進行評估像素與類別之間的對應關系和空間約束變換實現圖像的精準分割。具體步驟如下。

1)利用K均值算法進行參數初始化μj和∑j。

2)E步驟。用當前的uj和∑j從式(7)估計αij的后驗概率。

3)M步驟。首先利用當前新的αij，從式(9)估計新的均值向量μj；其次，利用當前新的αij，從式(10)估計新的方差∑j。

4)收斂。算法達到最大迭代次數或者小于給定閾值。

3 實驗結果與分析

實驗樣本圖像來自在遙感圖像場景分類數據集NWPU-RESISC45[14]，樣本為bridge_321，像素大小為256像素×256像素。本次實驗選擇的操作環境為：Intel(R)Core(TM) i5 7 200 CPU@2.50 GHz處理器、Windows 10 64位操作系統，以MATLAB R2010b為工具開展算法驗證以及相關性能的測試活動。

實驗步驟：1)測試本文所提出遙感圖像分割算法的分割效果及收斂性；2)測試溫度系數對遙感圖像分割結果的影響；3)與其他分割算法的性能對比分析。算法參數初始值由K均值方法獲取，分割類別數量K=3，溫度系數β取值范圍為[0.5，8]。

算法在下面的條件之一將停止：1)連續2次分割結果的改變比率不超過0.001；2)迭代次數超過50。

3.1 樣本分割性能測試實驗

1) 算法收斂性實驗。本節實驗主要驗證本文算法的分割效果和算法的收斂性，溫度系數β設置為1，圖1所示為樣本圖像的分割結果。圖1(a)為原始遙感樣本圖像；圖1(b)～圖1(d)分別為不同迭代次數下的分割效果，迭代次數依次為2、5和50。從遙感圖像的分割過程來分析，在迭代開始時，圖像中的孤立像素不僅數量較多，同時分布也十分密集，部分背景區域容易被劃分為目標區域，而且不同目標區域之間處于連貫狀態，不滿足原始影像的要求。隨著迭代次數的增加，遙感樣本圖像線條復雜細節區域的分割邊緣細節更為精確和完美，圖像余留的噪聲點逐漸減少，同時較小的區域能夠被良好分割，盡管仍然存在少量的錯分情況，但是由于對數函數減弱了權重造成的影響，所以能夠較好地劃分所有像素的能量。

圖1 分割結果

圖2顯示本文的條件期望似然函數最大化過程中的量化值。通過連續5次迭代操作，實現了快速收斂的目的，所以本文方法可以直接通過EM算法來達到優化參數的目的，與其他方法相比，具有速度快、容易操作、效率高等優勢。

圖2 收斂過程

2) 溫度系數對分割影響實驗。本節實驗主要驗證不同溫度系數因子對樣本圖像分割效果的影響，實驗結果如圖3所示。圖3(a)～圖3(d)分別為溫度系數β為0.5、2、4、8時的分割結果。通過分析，如果選擇β值足夠小，能夠實現高精度的分割，同時目標輪廓與真實輪廓之間也更加接近。然而分割結果圖像中會存在較多的噪聲點，無法準確地分割較小的區域且較小區域的分割結果呈離散狀，此時該方法魯棒性很弱，易于誤分類。如果所選擇的β值足夠大，圖像中的噪聲點大量減少，但是，分割的細節會丟失(例如左上角的橋梁)，較小的區域容易連通(例如河道中間的橋梁)。圖4顯示了不同溫度系數下本文所提出的遙感圖像分割算法對測試遙感樣本圖像分割結果的誤分率曲線。分割誤分率曲線顯示在β為4的時，遙感圖像正確分割性最高。

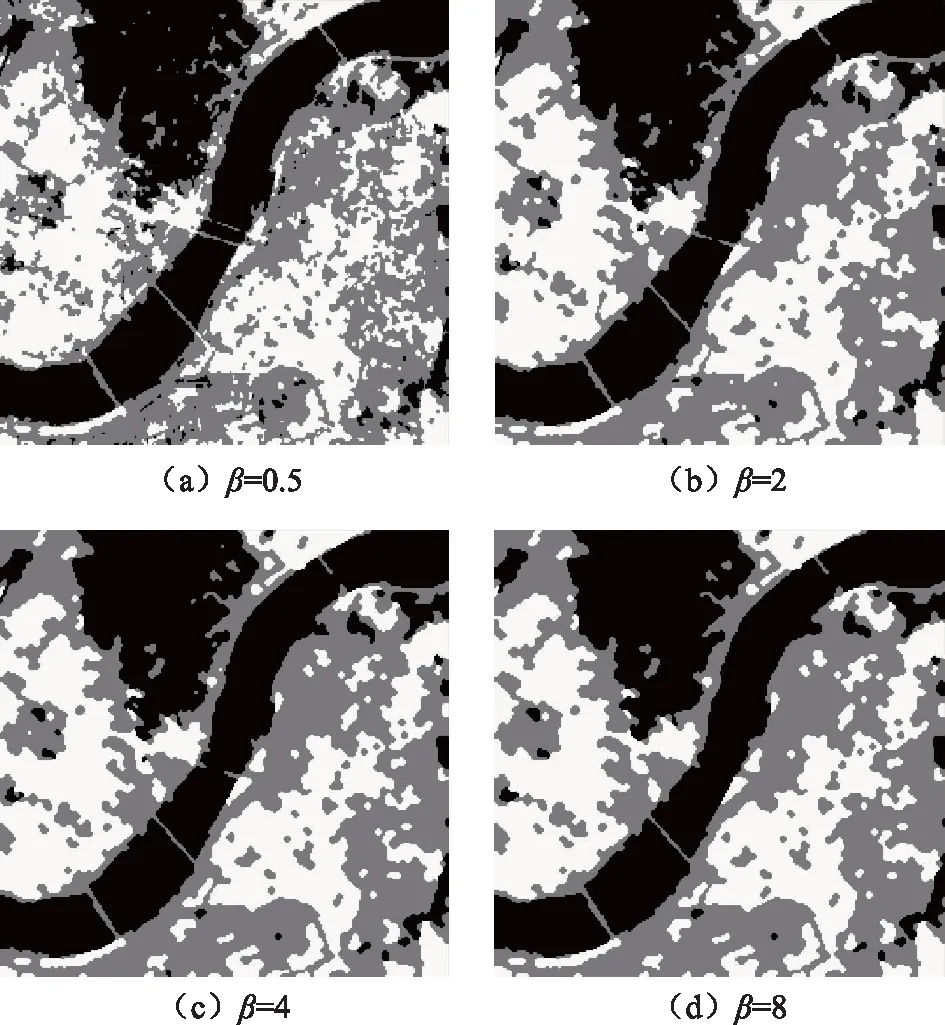
圖3 不同溫度系數β下分割效果

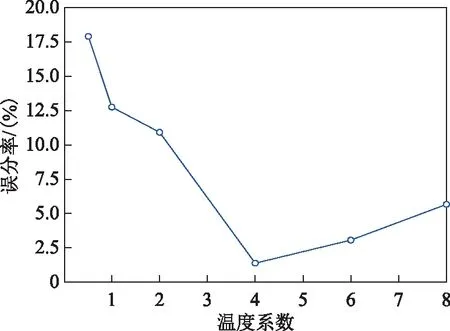
圖4 溫度系數β對誤分率影響曲線

3.2 遙感圖像的不同分割算法對比分析實驗

本節對深度學習[15]、GMM以及MRF傳統分割算法進行了定性和定量對比分析，以驗證本文算法的優勢。實驗參數設置為：類別區域數為3，β=4，并且選用Jaccard相似度RJ及分類正確率RCCR作為性能衡量指標[16]，RJ和RCCR的取值范圍為0到1，數值越大說明算法的分割效果越佳。

圖5顯示不同算法的遙感圖像分割結果。圖5(a1)～圖5(a4)分別為傳統GMM算法、深度學習算法、MRF算法及本文算法的遙感圖像分割結果，圖5(b1)～圖5(b4)為圖5(a1)～圖5(a4)中紅色方框區域放大2倍顯示結果。圖5說明，參與對比的3種分割算法盡管能夠實現分割目標區域的目的，然而分割區域存在著部分噪聲以及無效區域，尤其是類之間的邊界難以檢測，所以傳統分割算法會受到噪聲影響，導致分割存在較為嚴重的錯誤。圖5(a1)GMM算法的分割效果較差，圖像中的孤立像素不僅數量較多，且分布十分密集，部分背景區域容易被劃分為目標區域，而且不同目標區域之間處于連貫的狀態，不滿足原始影像的要求；圖5(b1)中河道內出現了大量錯分點，并且河岸的邊界輪廓產生階梯和毛刺干擾現象；圖5(b2)為深度學習的分割結果，由于缺少大量訓練樣本，雖然分割效果較好，但是橋梁出現不完整的過分割顯現；圖5(b3)的河道內出現錯分點且背景出現較多的干擾；圖5(b4)為本文所提出分割算法的圖像分割結果，能夠實現精準分割，同時受噪聲影響較小，與其他算法相比，分割效果最佳。

表1是不同分割算法的性能評價參數。性能評價結果表明：1)在深度學習算法、GMM算法、MRF算法分割結果圖像中均存在十分明顯的錯誤分類情況以及大量的噪聲點，所以它們的指標參數水平較低，而本文采用的分割方法能夠實現更準確的分類，同時對噪音的抑制能力也越強；2)因為本文算法可以通過EM算法方式來優化目標似然函數，其他方法不能夠進行先驗分布操作，所以本文算法方法具有易操作、效果好的優勢。

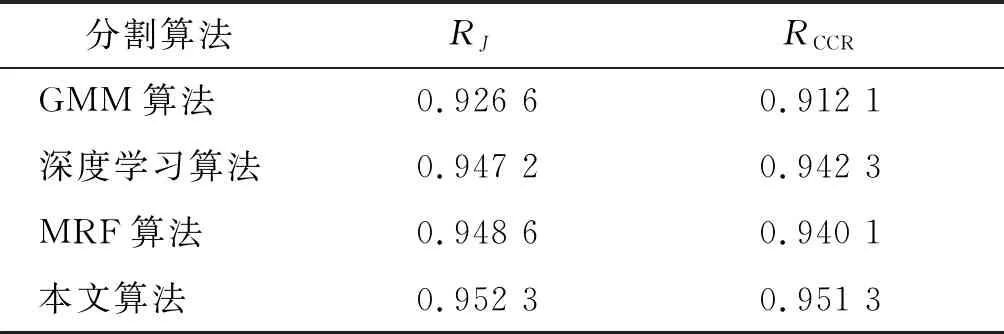
表1 不同算法定量分析統計結果

4 結束語

本文詳細介紹了一種基于馬爾科夫隨機場的高斯混合模型的遙感圖像分割方法。首先，根據圖像區域特征，利用像素之間的空間信息對高斯混合模型的先驗概率和后驗概率進行約束，定義的空間約束能夠確保圖像在進行空間更新時結構的穩定；其次，根據空間像素區域分類信息，通過能量函數中灰度信息的分量控制，確保圖像灰度和空間信息的自適應分配，同時通過鄰域相關性定義先驗概率的引入，提高分割算法對噪聲的魯棒性；最后，利用K均值方法初始化高斯混合模型參數，通過EM算法準確地完成圖像的分割。通過性能測試和比較實驗，驗證了本文算法的分割性能。