考慮截面形變的伸縮臂臂架動力學特性研究*
謝 瑤,張 磊*,唐亞鳴,丁根宏
(1.河海大學 機電工程學院,江蘇 常州 213022;2.河海大學 理學院,江蘇 南京 210098)
0 引 言
伸縮臂臂架常見于起重機、挖掘機和高空作業車等工程機械中,廣泛應用于建筑、消防等行業[1,2]。在工作過程中,伸縮臂臂架截面由于外力的原因容易產生拉伸、彎曲等變形[3],直接影響到工程設備的工作性能。對此的相關研究方面,傳統的梁理論忽略了翹曲、畸變等高階變形,難以反映臂架真實的力學行為,所以有必要深入研究伸縮臂臂架的動力學特性。
針對伸縮臂臂架的動力學分析,國內外學者進行了深入的研究。王志彪、蒙樹立[4,5]將臂架模擬成柔性體模型,結合柔性多體動力學和基礎振動理論,建立了臂架的剛性模型和柔性模型;都亮[6]對高空作業車模型進行了運動彈性動力學分析,并基于KED方法對臂架系統的多柔體動力學方程進行了求解;李濤等[7-9]將臂架簡化為具有端部質量的變截面階梯梁,基于梁的振動理論,結合邊界條件和連接處連續性條件,建立了伸縮臂的動力學模型,李圣[10]和SAWODNY O[11]基于哈密頓原理推導了各節臂架的振動方程,求解了臂架前三階振型函數及固有頻率。但在以上的研究中,臂架的動力學模型大都是通過解析法建模,求解過程復雜,且在建立臂架模型時很少考慮截面畸變、翹曲等高階形變對于臂架動力學的影響,使得計算結果存在一定的誤差。
本文考慮包括臂架截面拉伸、扭轉、畸變、翹曲等形變的完全耦合,根據廣義位移和廣義坐標建立截面中線上的位移場,結合哈密頓原理,分別建立臂節和伸縮臂系統的動力學模型,并通過數值算例驗證其可行性;同時分析在不同幾何參數條件下,高階特征形變對伸縮臂振動性能的影響。
1 伸縮臂系統的物理模型
本文考慮兩節臂架的伸縮臂系統,將伸縮臂簡化為一端固定的矩形薄壁梁,認為第一節臂架的內表面和第二節臂架的外表面在連接處固定貼合。
伸縮臂結構簡圖如圖1所示。
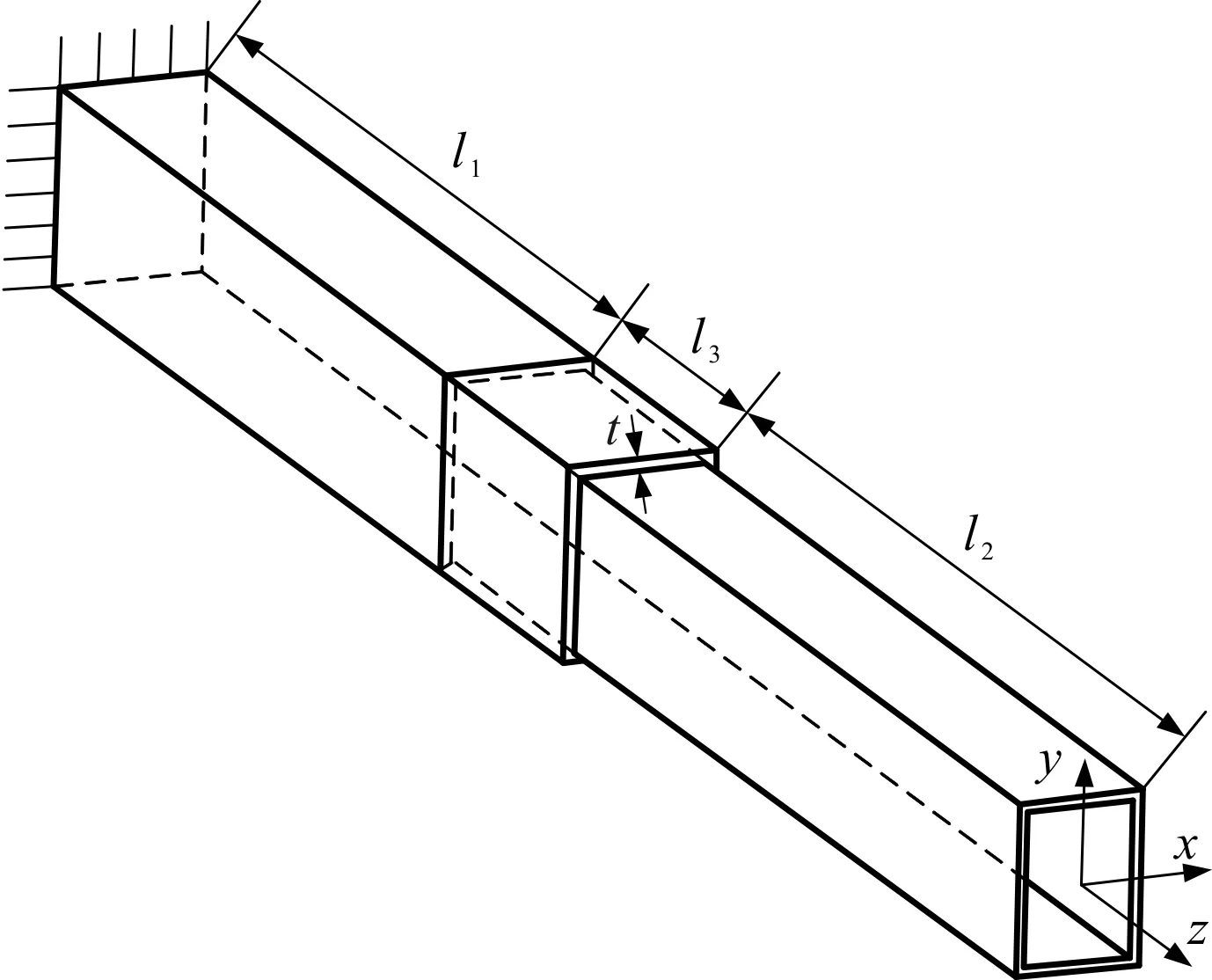
圖1 伸縮臂結構簡圖
圖1中,以臂架截面中心為原點建立空間坐標系(x,y,z),兩節臂架長度分別為(l1+l3)和(l2+l3),兩節臂架的厚度均為t。
2 伸縮臂系統的動力學建模
2.1 臂節的動力學模型
在考慮了截面變形對于臂節動力學建模的影響基礎上,筆者在截面中線上建立局部坐標系,如圖2所示。
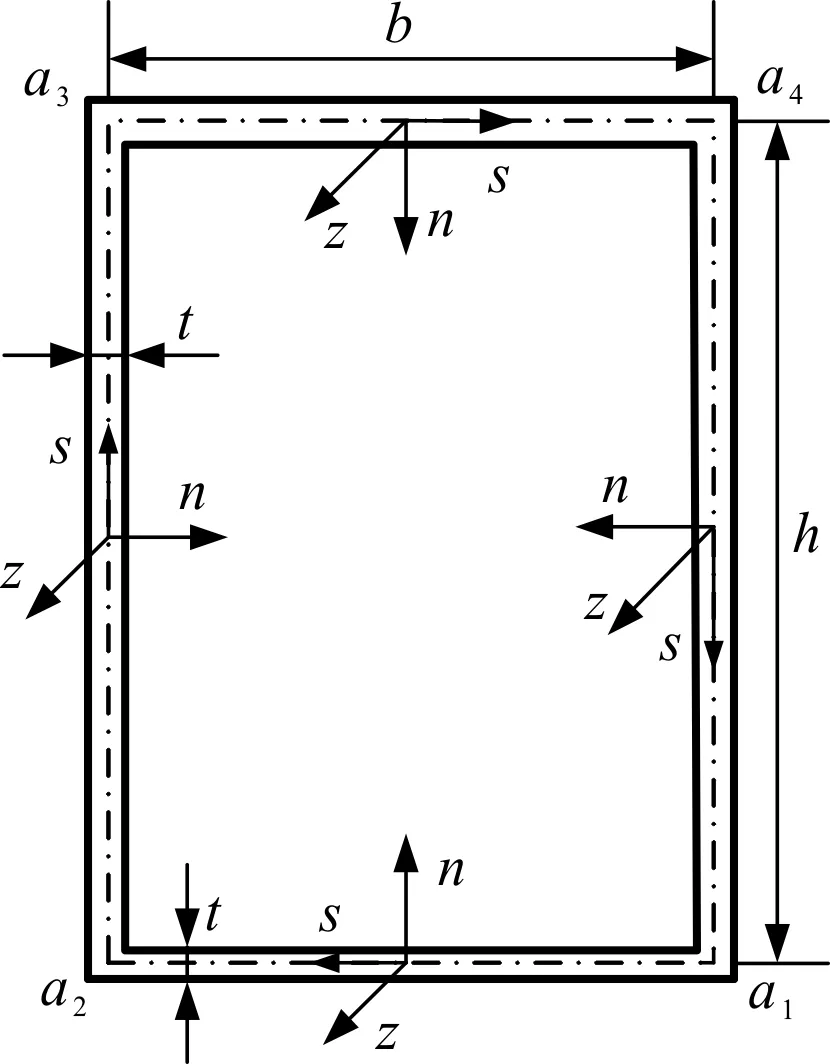
圖2 截面中線上的局部坐標系
圖2中,截面寬度和高度分別為b和h,局部坐標系由切向s、法向n和軸向z定義,用于描述截面在各個方向上的變形。其中,切向坐標s以a1為起點沿截面中線逆時針方向,法向n與s垂直并指向壁板內側。
本文借鑒張磊[12]對矩形薄壁梁的分析方法,通過考慮截面8種變形模式來完成臂節的動力學建模。
變形模式如圖3所示。
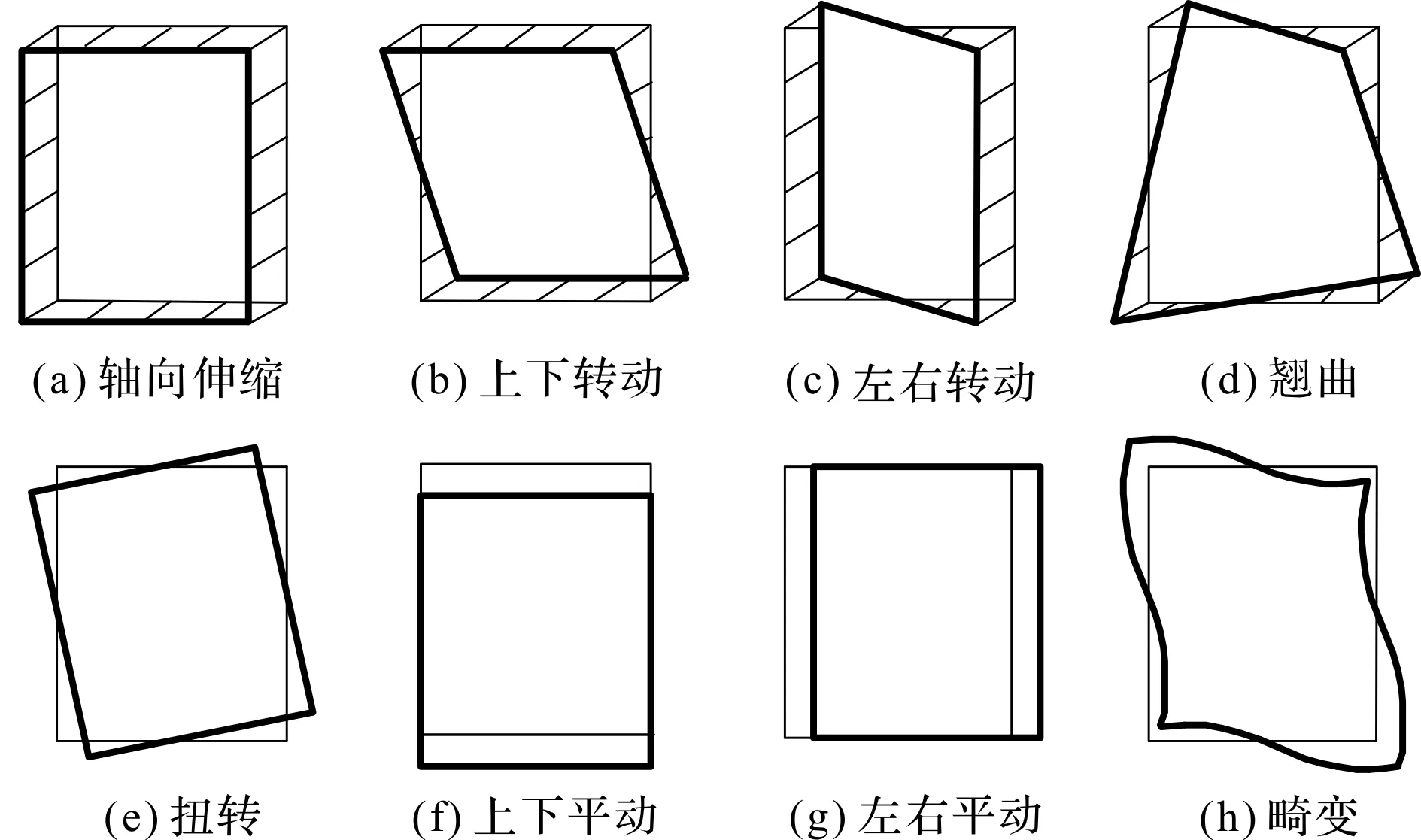
圖3 變形模式
圖3中,變形模式圖3(a~c,e~f)是基于鐵木辛柯梁理論的低階特征形變,變形模式圖3(d,h)是基于翹曲和畸變的高階特征形變;變形模式的形函數推導方法可以直接借鑒[13]。
筆者采用模態疊加的方法,將定義在臂架軸線上的截面變形模式的形函數線性疊加,用軸向u(s,z)、切向v(s,z)和法向w(s,z)3個位移分量來表示截面中線上點的位移,即:
(1)
式中:φ(s)—平面外變形的廣義坐標;ψ(s),ω(s)—平面內變形的廣義坐標;χ—廣義位移向量。
χ=[χ1(z)χ2(z) …χ8(z)]T
(2)
二維位移分量b可以表示為:
b=ψχ
(3)
式中:ψ—變形模式對應的廣義坐標。
(4)
三維位移場B(u,v,w)可由二維位移分量b轉換而得:
B=Lb
(5)
式中:L—微分算子。
(6)
根據哈密頓原理有:
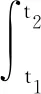
(7)
式中:T—臂架的動能;U—臂架勢能;W—外力勢能。
且有:
(8)
式中:ρ—臂架材料密度。
(9)
式中:ε—應變向量;σ—應力分量。
即有:
ε=CB
(10)
σ=Ehε
(11)
式中:C—微分算子;Eh—本構矩陣。
即:
(12)
(13)
式中:E—楊氏模量;v—泊松比;G—剪切模量。
W為:
(14)
式中:Λ—軸向的積分區域;Ω—s坐標的積分區域;n—薄壁梁的外表面;p,q—作用在臂架截面上的分布力列向量。
將式(8~14)代入式(7),可得:
(15)
將式(2~6)代入式(15),即可得到控制微分方程的具體形式。
本文采用有限單元法求解臂節的控制方程,通過拉格朗日插值函數沿軸線方向將臂節離散為n個單元,即:
χ=Ndi,i=1,2…n
(16)
式中:i—單元節點號;N—線性插值形函數;d—單元i的節點位移向量。
且有:
(17)
di=[χ1(i) …χ8(i)χ1(i+1) …χ8(i+1)]T
(18)
式中:ξ1,ξ2—形函數;(i),(i+1)—單元兩端。
則臂節總體節點位移向量Dr可以表示為:
Dr=[χ1(1) …χ8(1) …χ1(n) …χ8(n)]T
(19)
將式(16~19)代入式(15),可得:
(20)
式中:l—單元長度。
并將控制微分方程的形式整理為:
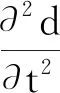
(21)
式中:m—單元質量矩陣;k—單元剛度矩陣。
(22)
(23)
筆者通過MATLAB編制相應的有限元程序,求解單元質量矩陣m和單元剛度矩陣k,結合邊界條件,組裝形成臂節的總體質量矩陣M1和總體剛度矩陣K1,其中:
(24)
(25)
式中:Tri—節點位移向量di到總體節點位移向量Dr的轉換矩陣。
2.2 臂架連接處動力學模型
筆者分別用兩節臂架的位移場來表示連接處的位移,理論上前一節臂架內表面與后一節臂架外表面在連接處位移應該相等,但考慮到模型簡化,兩種位移場表示的位移存在一定的差值,借鑒JANG等[14]在研究薄壁梁的處理方法,認為在位移場差值最小條件下的計算精度最高。
用兩節臂架的位移場表示連接處的位移,即:
Br1=Lr1ψr1Ndr1
(26)
Br2=Lr2ψr2Ndr2
(27)
兩節臂架在連接處的位移場差值可以表示為:
(28)
將式(26,27)代入式(28),當差值取極值點時最小,即:
(29)
式中:T—dr1與dr2之間的轉換矩陣。
考慮到(Lr1ψr1N)T不恒為0,即有:
Lr1ψr1Ndr1-Lr2ψr2NTdr1=0
(30)
轉換矩陣T可以表示為:
T=(T2)-1T1
(31)
式中:T1,T2—轉換矩陣。
T1,T2分別為:
(32)
(33)
2.3 伸縮臂系統的動力學建模
參考臂節的建模方法對第2節臂架進行動力學建模,考慮臂架連接處的位移連續性,完成伸縮臂系統的動力學建模。
兩節臂架的運動方程分別為:
(34)
(35)
式中:D1,D2—對應臂架節點位移向量。
將兩節臂架的節點位移向量分別用伸縮臂整體節點位移向量D表示,則有:
D1=TaD
(36)
D2=TbD
(37)
式中:Ta,Tb—轉換矩陣。
依據臂節模型離散方法,將兩節臂架依次離散為n1和n2個單元,且連接處為n3個單元,則伸縮臂共有(n1+n2-n3)個單元,且不考慮固定端的位移向量,則共有(n1+n2-n3)個獨立節點,則有:
Ta=[I8n1×8n108n1×8(n2-n3)]
(38)
(39)
n=8n3-16n2+32
(40)
將伸縮臂系統的整體運動方程表示為:
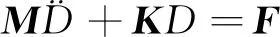
(41)
則有:
M=(Ta)TM1Ta+(Tb)TM2Tb
(42)
K=(Ta)TK1Ta+(Tb)TK2Tb
(43)
式中:M—質量矩陣;K—剛度矩陣。
3 數值算例與動力學特性分析
利用MATLAB求解質量矩陣和剛度矩陣的廣義特征值,即可轉化得到系統的固有頻率。因此,筆者通過比較本文模型與ANSYS模型計算結果的差異,分析在不同尺寸、不同邊界條件下,高階形變對于臂架動力學特性的影響。
3.1 算例1:臂節模型
臂節模型取伸縮臂結構的左端一節。參數包括:長度l1=0.55 m,l3=0.05 m,臂節截面b1=0.065 m,高度h1=0.086 m,厚度t=0.005 m,密度ρ=7 850 kg/m3,彈性模量E=2×1011Pa,泊松比v=0.3。
考慮到臂節模型的收斂性,此處的一維高階模型將臂節離散為60個單元;ANSYS模型采用shell181單元,控制單元尺寸為10 mm,將模型離散為1 920個Shell 181單元,其中沿臂架軸向60個單元。
臂節模型前10階固有頻率的比較如表1所示。
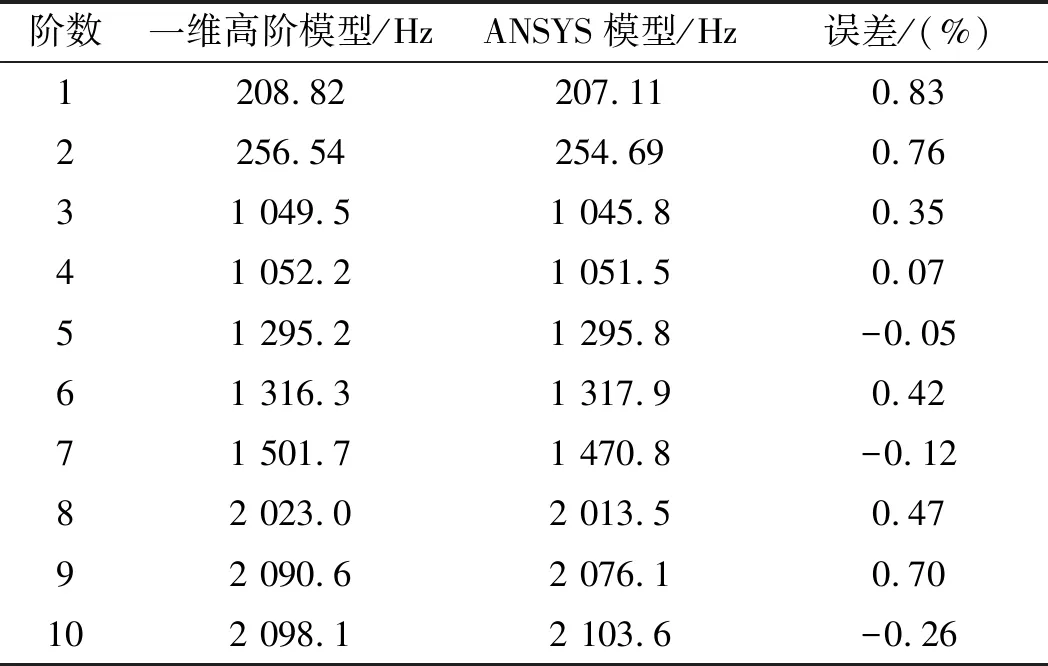
表1 臂節前10階固有頻率的比較
表1數據表明,此處的一維高階模型與ANSYS模型計算結果吻合良好,誤差在1%以內,驗證了臂節動力學模型的準確性。
與傳統的鐵木辛柯梁理論模型相比,本文高階模型的優點在于考慮了截面翹曲和畸變的影響。
筆者對不同幾何參數的臂節模型進行數值分析,分析高階特征形變對于臂節動力學特性的影響。
不同長度的臂節模型前6階固有頻率對比如表2所示。
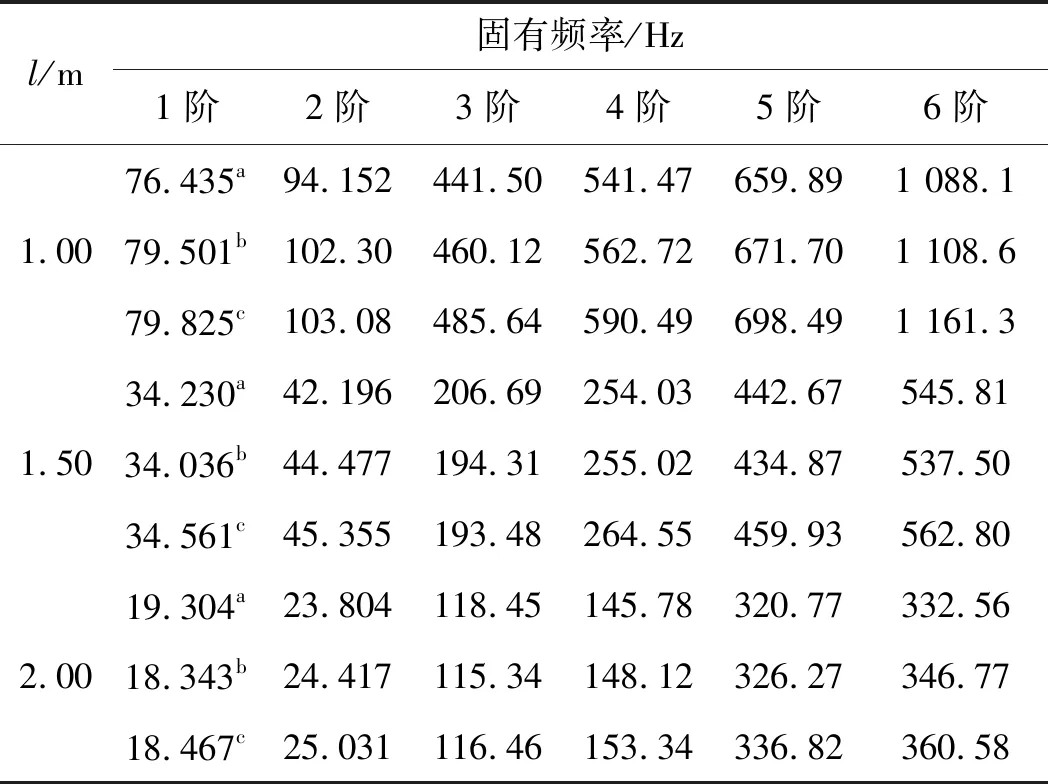
表2 不同長度的臂節模型固有頻率對比
表2中,在不同臂節長度下,本文模型的計算結果與ANSYS結果吻合良好;且對比數據發現,臂節模型的固有頻率隨著梁體長度的增加而減小。
不同厚度臂節前6階固有頻率對比如表3所示。
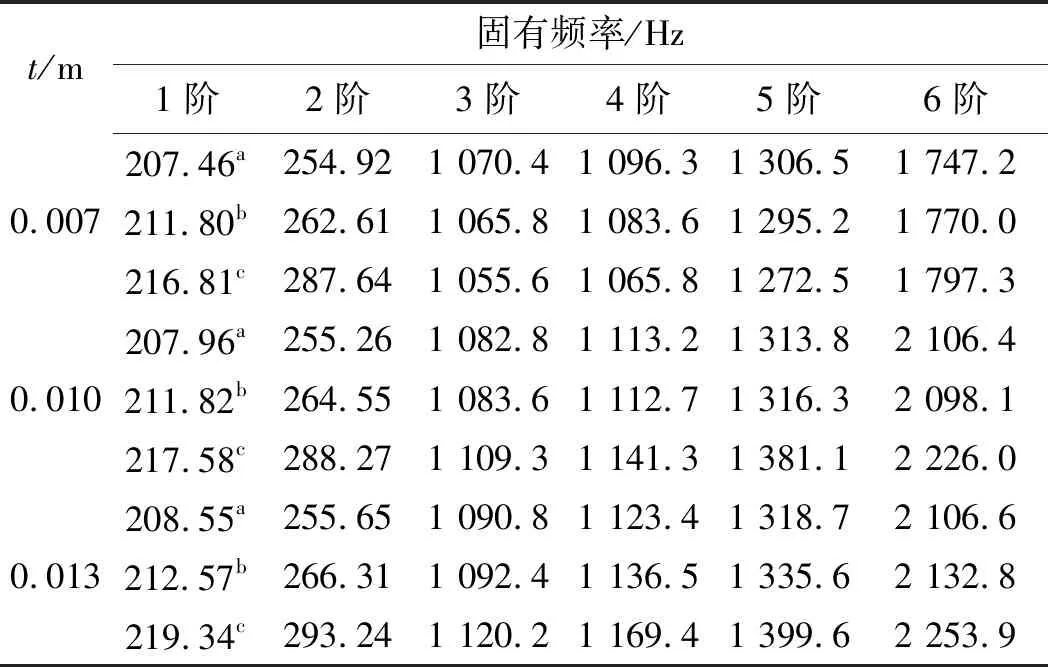
表3 不同厚度的臂節模型固有頻率對比
表3中,在不同臂節厚度下,本文模型的計算結果與ANSYS結果吻合良好;且臂節模型的固有頻率隨著臂架厚度的增加而增加。
綜合以上數據表明:(1)本文的一維高階模型適用于不同幾何尺寸臂架的求解;對于長度越長、厚度越小的臂架,一維高階模型和鐵木辛柯梁模型的計算結果相差越小,表明此時高階特征形變對于臂架振動的影響越小;(2)兩者的計算結果在前2階時差別不大,表明此時高階特征形變的影響可以忽略,但隨著模態階數的增大,兩者誤差呈增大趨勢,此時高階特征形變的影響不能忽略,否則誤差最高可達10%的。
與ANSYS相比,本文方法將臂節離散為較少的單元,有著更高的計算效率,對不同幾何參數的臂架,只要修改對應模型參數即可,無需重新建模。
不同邊界條件下,ANSYS模型、本文模型和Timoshenko梁模型的前20階固有頻率對比如圖4所示。
由圖4可知,在不同邊界條件下,一維高階模型與ANSYS模型結果都吻合良好;但在兩端固定條件下,一維高階模型與鐵木辛柯梁模型二者的差值明顯,表明兩端固定約束下,高階特征形變對于臂架振動的參與度更高。
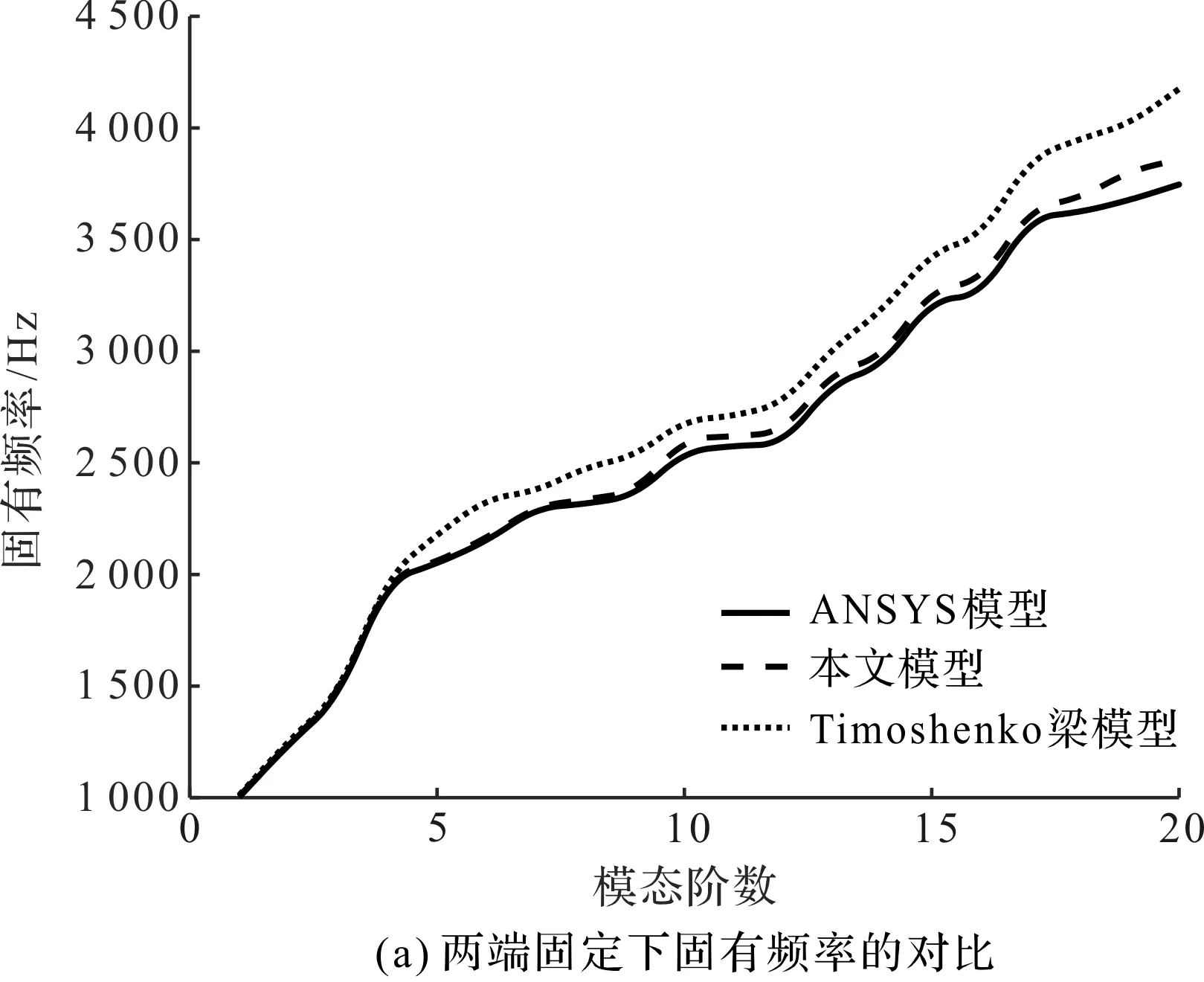
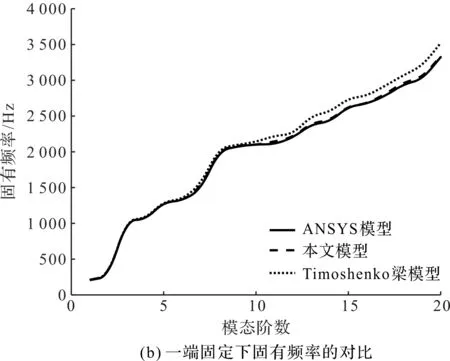
圖4 不同邊界條件下固有頻率對比圖
3.2 算例2:伸縮臂模型
伸縮臂的結構如圖1所示,其長度l2=0.75 m,截面寬b2=0.055 m,高度h2=0.076 m,其他參數同上。
一維高階模型將伸縮臂沿軸線方向離散為135個單元;兩節臂架在連接處可認為處于固定約束,ANSYS模型通過耦合所有方向自由度來模擬兩節臂架的接觸情況,單元尺寸為10 mm,共離散為3 880個Shell 181單元,其中沿臂架軸向為135個單元。
伸縮臂前10階固有頻率的對比如表4所示。
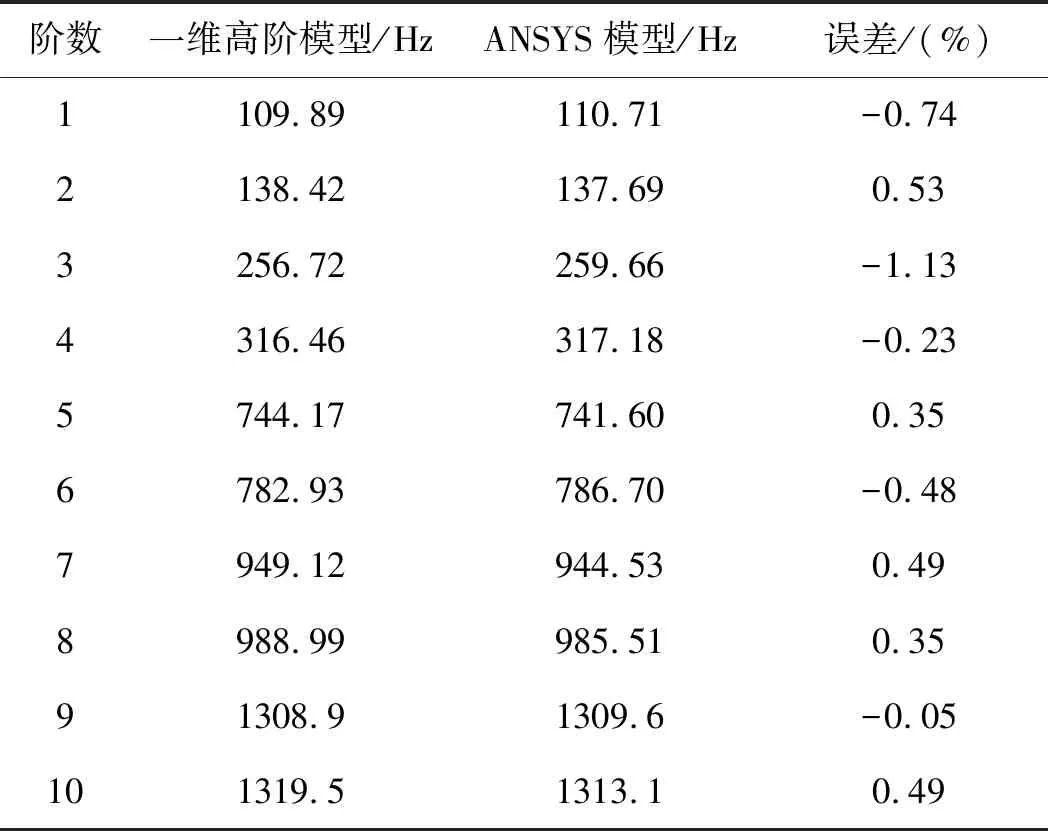
表4 伸縮臂前10階固有頻率的比較
表4數據表明:一維高階模型與ANSYS模型計算出的伸縮臂固有頻率結果吻合良好,誤差在1.2%以內,由此驗證了伸縮臂模型的可靠性。
不同連接處長度的伸縮臂模型前6階固有頻率對比如表5所示。
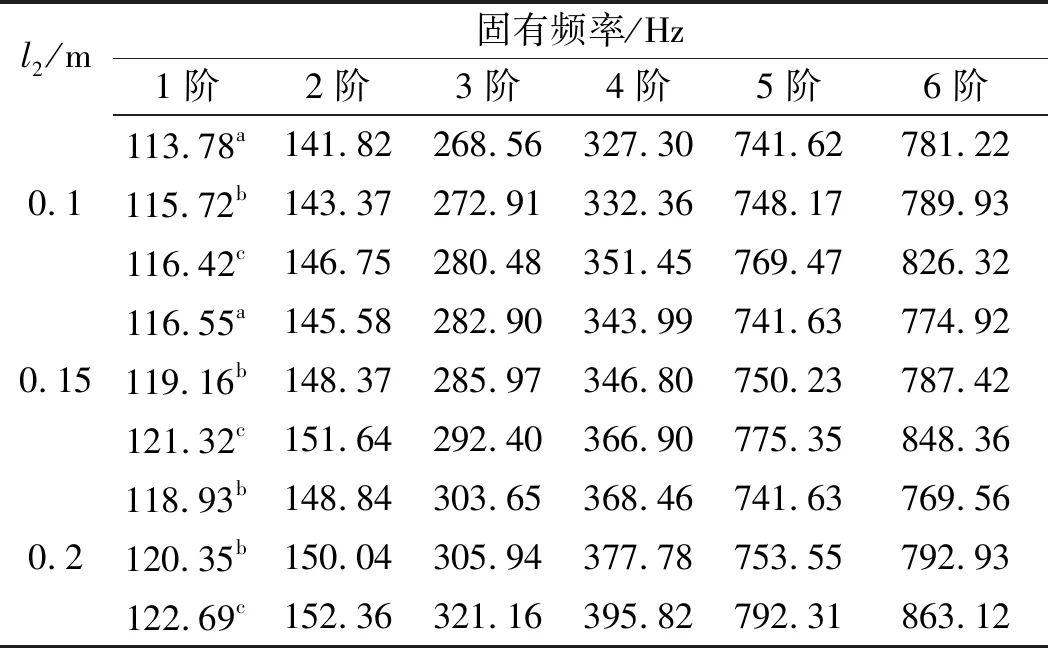
表5 不同連接處長度(l2)的伸縮臂固有頻率
表5數據表明:隨著長度l2的增加,伸縮臂整體長度減小,固有頻率總體上呈緩慢增大趨勢,與臂節模型的變化規律吻合。
4 結束語
針對伸縮臂臂架動力學建模繁瑣、求解復雜和精度不高的問題,筆者提出了一種考慮截面變形模式的伸縮臂臂架動力學建模及其求解方法,并且得到了如下的研究結論:
(1)與ANSYS相比,本文方法有著更高的計算效率,對于不同幾何參數的臂架,只要修改對應模型參數即可,無需重新建模;
(2)本文對于臂節模型和伸縮臂系統建立的動力學模型與ANSYS計算結果吻合良好,證明該方法是可靠的;
(3)對于伸縮臂系統前2階模態,高階特征形變可以忽略;高于2階模態,一維高階模型和鐵木辛柯梁模型的計算結果出入較大,此時必須考慮翹曲和畸變高階特征形變的影響,且隨著模態階數的增大,高階特征形變對臂架振動的參與度越高;
(4)臂架的固有頻率隨著梁體厚度的增加而增加,隨長度的增加而減小,隨高度的增加而減小。

