基于Copula 理論的序列型地震動隨機模型

申家旭，陳 雋，丁 國

(1. 同濟大學土木工程學院，上海 200092；2. 華東建筑設計研究總院，上海 200002)

歷史地震資料表明，一次大地震發生后，存在再發生多次地震的可能性，后續發生的這一系列地震被稱為余震，主震與余震共同組成序列型地震動，在其作用下，已損傷結構會發生二次損傷，甚至造成倒塌。最典型的是2010 年的新西蘭基督城地震，7.0 級的主震使城市中的小部分建筑遭受了嚴重破壞，而數月之后的6.3 級的強余震使已損傷的建筑進一步受損，導致了大量建筑破壞和倒塌，造成了比主震嚴重的多的經濟損失和人員傷亡[1]。在我國1999 年集集地震以及2008 年汶川地震中，序列型地震動不僅造成了大量的結構破壞，而且加大了災后救援的難度，使人民的生命財產受到了嚴重損失。研究序列型地震動的特性和生成模型，成為工程結構抗震研究中一個重要的現實問題。

地震動的合理數學模型是工程結構抗震分析的基礎。1947 年，Housner[2]指出工程結構在地震作用下的響應主要受兩個因素的影響：一是結構自身的動力特性；二是地震動的特性。根據當時為數不多的地震動記錄，Housner[2]認為實際地震動具有很強的隨機性，并提出了最早的隨機地震動模型——隨機獨立脈沖模型。近幾十年來，世界各國陸續建立了覆蓋面廣的強震觀測臺網，極大地豐富了序列型地震動的實測數據，為人們認識和研究地震動提供了良好的數據基礎。基于大量的觀測記錄，不同的地震動模型相繼提出，其中具有代表性的有Kanai-Tajimi 模型[3?4]、譜表現方法[5?6]、演變功率譜模型[7]等。這些模型從不同角度表現了地震動的特性，并得到了廣泛的應用。對于序列型地震動的模擬，早期的研究主要以重復主震或隨機組合主余震記錄[8?10]等方式來實現。然而，多位研究者已指出此類方法會過高地估計結構響應[11?13]。現行方法則主要集中在建立主震與余震地震動強度參數[14?18](如震級、PGA等)之間的統計學關系，通過隨機地震動模型(如Kanai-Tajimi 譜模型等)分別生成主震和余震，或通過地震動衰減關系挑選主震和余震。此類方法實質上是主震隨機模型，伴隨的余震是由主余震之間的確定性關系而唯一確定的。此外，很多主震隨機模型本身基于平穩性假定，與地震動實際非平穩特性不符。事實上，主震和余震在地震強度、頻譜和持時等方面均密切相關，僅通過單一的地震動強度參數來反映二者的關系，顯然不能準確全面地刻畫出余震的特征。此外，考慮地震動發生機理的多因素特征，余震同樣具有相當的隨機性。因此，對主震和余震間相關性的研究，以及對地震動隨機性和非平穩性的合理表征，是建立序列型地震動模型的關鍵難題。

聚焦于城市中某一區域(100km2～101km2)的抗震分析，覆蓋面再廣的觀測臺網中也僅會有少量的臺站可以記錄到由震源傳遞至此區域的地震動。而受到地震波傳播過程中的行波效應、場地效應等因素的影響，區域中任一點的地震動均存在顯著的空間變異性[19]，僅靠臺站得到的數條單點地震動難以準確表達此區域中每棟建筑所承受的地震動。因此，對于城市區域建筑群的抗震研究，建立合適的序列型地震動場模型以反映城市區域中每一點處的地震動也是亟待解決的關鍵問題。

在一場大地震中，余震往往會發生非常多次，然而，多數余震震級較小，對結構安全影響較小。在結構抗震分析中，學者們普遍關注主震與最大余震的組合，即“主震+最大余震”型序列型地震動。本文的研究對象即為“主震+最大余震”型序列型地震動。

綜上，本文從地震動產生的物理機制出發，在已有的工程場地地震動模型的基礎上，考慮主震與余震在產生、傳播機制上的相關性，利用Copula 理論研究主震和余震各參數相關性，進而考慮局部場地上不同點的空間相關性，形成序列型地震動隨機場模型。

1 Copula 理論

Copula 理論最早由Sklar[20]提出，即任意一個多元聯合分布都可以分解為相應的多個邊緣分布和一個Copula 函數，該Copula 函數唯一地確定了變量間的相關性。后經眾多研究者的不斷發展，Copula 理論已經成為了解決高維隨機變量聯合概率分布問題的有效手段。Copula 理論的優勢在于將變量邊緣分布函數的估計與Copula 函數的選擇分開獨立進行，并引入描述變量間非線性關系的秩相關系數，能夠更加準確地描述變量的相關性。Copula 理論最早應用于金融、保險等領域，隨后在水文學中得到廣泛應用。相對來說，其在地震工程中的應用還處于起步階段。僅有少量研究者將Copula 理論引入地震動與結構抗震的研究中。Goda 和Salami[21]基于Copula 函數建立了地震作用時結構最大變形和殘余殘余變形之間的關系；朱瑞廣和呂大剛[22]利用Copula 函數分析了主震和余震34 個地震動強度參數的相關性，并基于Copula 理論提出了余震的條件均值譜模型[17]。

Copula 理論為確定兩個或多個隨機變量間的聯合概率分布函數提供了一條有效且便捷的途徑。前已述及，Copula 理論中引入了描述變量相關性的相關系數，其中應用較為廣泛的為Pearson線性相關系數，Kendall 秩相關系數以及Spearman秩相關系數。本文選取能夠反映變量間非線性關系的Kendall 秩相關系數作為變量間相關性的度量。由Kendall 秩相關系數及參數的邊緣分布，即可根據Copula 函數建立變量間的聯合概率分布函數。以二維隨機變量為例，其聯合概率分布可表示為：

式中：F1(x1)、F2(x2)為變量x1和x2的邊緣累積分布函數；u1=F1(x1)，u2=F2(x2)，均為[0,1]間的均勻分布；C(u1,u2)為Copula 分布函數，其變量區間為[0,1]；θ 為與Copula 分布函數對應的相關參數，可由對應的Copula 分布函數及Kendall 秩相關系數求出。

為確定序列型地震動中主震與余震的相關性，本文采用Copula 理論定量分析并確定了主余震物理參數間的相關關系，并給出其顯式表達。

2 序列型地震動隨機場物理模型

主震與余震地震動參數之間的關系一直是地震學領域的研究重點。在地震動研究的早期，描述主震與余震關系的地震學三大定律[23?25]相繼提出。隨后的數十年里，大量的研究者們對其進行了修正和改進，力求真實地反映主余震的關系。而在地震工程學領域，研究者們更多地關注影響結構安全性的參數(如PGA、PGV、Sa 等)，著眼于將地震動參數與結構時程分析或譜分析相結合，研究主余震之間卓越周期、譜加速度等參數的相關性，以指導工程實踐。如前所述，現有方法一般通過主余震地震動參數的統計關系來建立序列型地震動模型。由于統計關系本身的經驗性特征，不能準確地體現主余震相關性的物理機制，且其本質是主震與余震一一對應的確定性模型，這與主震過后往往出現大量隨機性余震的事實不符。更為關鍵的是，大量的地震事件表明：主震與余震在震源及傳播途徑上并不完全相同，主震斷層的二次破裂及臨近斷層的破裂均會產生余震，因此，將主震與余震視為完全相關并不能準確表達出余震的自身特性。

2.1 序列型地震動物理隨機函數模型

為克服描述單次地震的現象學隨機地震動模型(如Kanai-Tajimi 譜模型，演變功率譜模型等)的經驗統計的局限性，Wang 和Li[26]從地震動“震源-傳播途徑-局部場地”的物理機制出發，在隨機Fourier 譜和隨機函數模型的基礎上分別對震源、傳播途徑、局部場地進行建模，給出了隨機地震動的Fourier 幅值譜和相位譜模型。模型中影響地震動隨機性的關鍵物理因素被抽象為隨機變量，由此得到了地表一點處的地震動模型。宋萌[27]在此基礎上優化了Fourier 相位譜模型，并將其中的經驗參數改為了隨機參數。基于上述兩項工作，場地一點處的地震動在時域范圍內可以表示為：

限于篇幅，此模型更詳細的理論推導可參考文獻 [26 ? 27]。

從地震動的物理機制出發可以發現，盡管主震與余震在地震動參數以及反應譜中表現出一定的相關性和差異性，但其均遵循“震源-傳播途徑-局部場地”的物理過程。而在這一物理過程中，其物理要素(即式(2)中的基本物理參數)具有不可完全觀測和不可完全控制性，因而伴隨主震而記錄到的余震必然表現出顯著的隨機性。主震與余震各物理要素在空間上的相關性決定了主震與余震時程的相關性。因此，研究主震與余震各物理要素之間的相關性即可反映出主震與余震時程的相關性，這也是序列型地震動建模的關鍵。

考察式(2)，其中的λ 為含有八個物理參數的隨機向量，可以看到，地表一點處的地震動加速度時程由λ 所決定。在地震動產生、傳播的過程中，震源空間位置的相關性導致了描述震源、傳播途徑的物理參數是存在相關性的。地震動在局部場地的傳播過程較為復雜，本文將局部場地的變化假定為線性，暫不考慮其非線性變化。因此，描述局部場地動力特性的物理參數ξg和ωg在主震和余震中可視為是并未發生改變的，而主震與余震的空間相關性寓于描述震源和傳播途徑的六個物理參數中。基于上述觀點，地表一點處的序列型地震動加速度時程可表示為：

2.2 序列型地震動隨機場物理模型

為描述地震動在局部場地上的空間相關性，Wang 和Li[28]基于地震動隨機函數模型(即地表一點處地震動模型)，考慮地震動場雙尺度建模，建立了工程場地地震動隨機場的物理模型。繆惠全和李杰[29]在此基礎上提出了工程場地地震動的相干函數模型，并與經典的Hao 模型、Harichandran-Vanmarcke 模型進行了對比，驗證了其合理性。場模型可表述為：

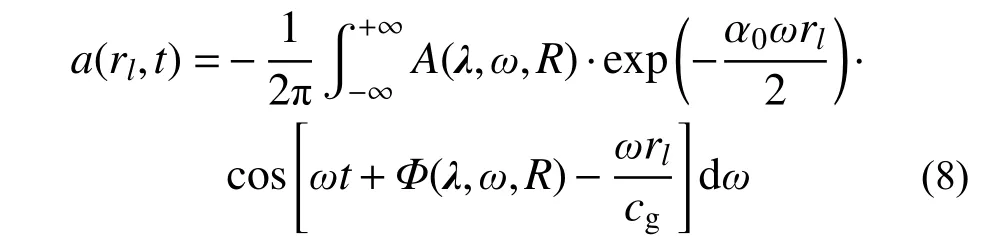
式中：rl為場地任意一點沿波的傳播方向上到場地中心的距離；α0為場地地震波衰減參數；cg為場地等效波速；a(rl, t)為場地內任意一點的加速度。

限于篇幅，隨機場模型更詳細的理論推導可參考文獻 [28 ? 29]。

該模型考慮了地震動的行波效應和場地效應，準確簡潔地反映了地震動產生、傳播過程中震源、傳播途徑和局部場地物理機制的作用。模型已應用于高層建筑[30]、超高層建筑[31]、大型冷卻塔[32]等單體建筑的抗震可靠度分析和倒塌模擬，以及地下管網系統[33]等區域性生命線工程的抗震可靠性分析，有良好的工程應用基礎。

第2.1 節，本文提出了地表一點處的序列型地震動模型。模型將同一地震事件中主震與余震視為兩個隨機過程，并進一步地考慮了兩個隨機過程中的隨機變量在震源、傳播途徑中的相關性。在考慮使用隨機場描述場地內各點序列型地震動的空間相關性時，由于余震震源位置存在不確定性，本文將地震動東-西分量與南-北分量視為相互獨立的地震動時程記錄，使用此方法處理，可將地表一點處主震與余震分量以相同方向表示。而由于本隨機場刻畫的是局部場地范圍內地震動的行波效應和場地效應，因此，隨機場的兩個物理參數α0和cg在主震和余震中視為相同的物理量。基于此，在工程場地范圍內，序列型地震動隨機場物理模型可表示為：

3 序列型地震動的參數識別和統計

為確定式(9)中各物理參數的概率分布及主余震參數的聯合概率分布，本節收集并篩選了不同場地類型的實測序列型地震動，并進行重采樣及歸一化處理；隨后對主震和余震各物理參數分別統計，識別出各參數的邊緣概率分布；最后根據各參數的相關系數及邊緣概率分布，識別出最優Copula 函數，給出式(9)中各二維參數的聯合概率分布。

3.1 實測序列型地震動的收集和處理

本文從太平洋地震工程研究中心[34](Pacific Earthquake Engineering Research Center, PEER)和KiK-net & K-NET 中收集得到了大量的序列型地震動記錄。通過如下準則對其進行篩選：

1) 選取一次地震動事件中主震和伴隨其發生的一系列余震中震級最大的一次余震；

2) 選取同一臺站記錄的主震和余震并組合；

3) 為避免土-結構的耦合作用，臺站位于自由場地或較小建筑物的地面層；

4) 主震和余震的震級分別不小于5 級，排除不太可能對結構造成影響的地震；

5) 為了研究場地類別對結構響應及損傷狀態的影響，將序列型地震動按場地類別進行分類，場地類別依據中國抗震規范劃分為四類場地，按照20 m 土層厚等效剪切波速VS20和30 m 厚等效剪切波速VS30劃分，劃分標準如表1。由于KiKnet & K-NET 按照分層土記錄土層信息，為便于分類，統一按照中國規范計算其VS20，計算依據參考郭鋒[35]提出的VS20與VS30轉換關系式。

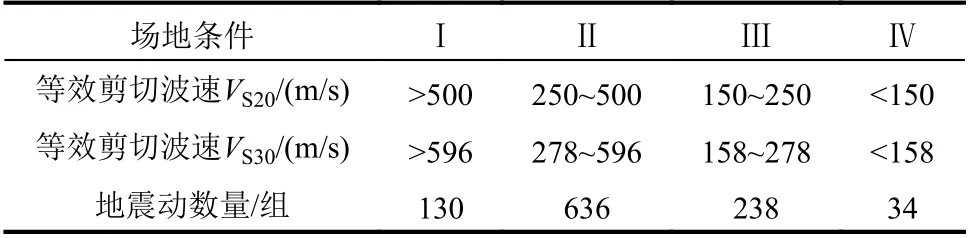
表 1 場地劃分標準及序列型地震動數量Table 1 Site classification standard and number of sequential ground motions

共篩選得到1038 組符合條件的序列型地震動，另外，選取了SMART1 臺陣測得的五組地震動場記錄以作地震動場參數的識別，其基本信息如表2 所示。本文主要研究地震動水平分量，故選擇各臺站記錄中的E-W 分量和N-S 分量，將其視為相互獨立的地震動處理。

表 2 篩選得到的實測序列型地震動Table 2 Selection of measured sequential ground motions

各臺站測得的地震動時程采樣頻率存在差異，為便于分析，統一將地震動以0.02 s 的時間間隔進行重采樣，頻率限為25 Hz。重采樣結果與原始地震動時程在時域和頻域的差異均極其微小，對識別結果的影響可以忽略。另外，地震動的峰值統一調幅至0.1 g，作幅值歸一化處理。

3.2 物理隨機參數的識別與統計

利用實測序列型地震記錄，針對第2.1 節和第2.2 節的模型參數的識別過程如圖1 所示。

圖 1 參數識別流程圖Fig. 1 Flowchart of parameter identification

1) 對地震動時程作Fourier 變換，得到其Fourier幅值譜和Fourier 相位譜；

2) 由式(2)的幅值譜模型，采用最小二乘準則擬合，識別主震幅值譜模型中的物理參數A0M、τM、 ξgM和 ωgM；

3) 將 2)中的局部場地參數 ξgM和 ωgM代入余震幅值譜模型中，識別余震模型中的參數A0A和 τA；

4) 利用真實地震動的相位譜，求得其相位差譜分布；

5) 將2)和3)中的震源系數τM和τA代入式(3)的相位譜模型中，采用最小二乘準則將模型的相位差譜與真實相位差譜分布擬合，利用遺傳算法識別分別得到主震和余震相位譜模型中的參數aM、bM、cM、dM和 aA、bA、cA、dA。

6) 對地震動場參數作識別，得到α0和cg。

在各參數中，幅值譜對應的A0M、τM、ξgM和ωgM以使模型逼近真實地震動幅值譜為原則，識別方法采用最小二乘法，可表述為：

遺傳算法的參數設置，如表3 所示。

表 3 遺傳算法參數設置Table 3 Settings of Genetic Algorithm

對于α0和cg的識別，首先識別出場地中心點 C00 的各物理參數 A0、τ、ξg、ωg、a、b、c、d，由最小二乘法確定幅值譜中的參數α0。對于場地等效波速cg，可通過下式識別：

式中：Δrl為兩樣本點在平面波場中的坐標差；Δt 為兩樣本的時間延遲，可采用Boissières 和Vanmarcke[36]提出的方法確定。

根據上述過程，對各組序列型地震動逐一識別，得到描述主震和余震的各物理參數在四類不同場地類型下的分布規律。考察其統計分布，采用貝葉斯信息準則(Bayesian Information Criterion，BIC) 準則[37]求得最優概率模型，獲得主震和余震各參數的概率密度函數，對應的概率密度函數統計值如表4 和表5 所示。表中參數P1、參數P2的含義：當概率密度函數為Normal 時，分別為均值和標準差；概率密度函數為Lognormal 時，為對數的均值和標準差；概率密度函數為Weibull 時，為形狀參數和尺度參數。需要指出的是，在對α0和cg進行識別前，應按照場地條件對地震動記錄進行分組以滿足工程需要。然而，用于觀測局部場地的地震動臺陣較少，易于獲取的地震動場記錄均來自于SMART1 臺陣，其對應的場地為Ⅱ類場地。因此，本文給出的α0和cg的統計結果嚴格來說僅適用于Ⅱ類場地。

表 4 概率密度函數及其對應參數Table 4 Probability density functions and parameters

表 5 概率密度函數及其對應參數Table 5 Probability density functions and parameters

以參數A0為例，圖2 給出了主震A0M和余震A0A的統計分布及其概率密度函數(Probability Density Function，PDF)曲線。其中BIC 定義為：

式中：f (xi; p, q, r)為概率分布函數的密度函數，xi(i=1, 2,···, N)為樣本點數目，p, q, r 為分布參數；k1為分布參數的數目。

3.3 主余震的相關性分析

以參數A0為例，圖3 給出了各類場地下主震A0M與余震A0A的關系，其中IV 類場地下收集到的地震動數量較少。分別計算各參數的Kendall 秩相關系數，A0、τ、a、b、c、d 的相關系數分別為：0.589、0.508、0.277、0.395、0.195、0.172。可知，主震與余震的參數間存在一定的相關性，本文通過引入Copula 理論對其進行描述，并給出主余震參數的聯合概率分布，實現對主余震參數相關性的顯式表達。

為此，根據第3.2 節中得到的各參數的邊緣分布函數，利用二維Copula 函數建立主震和余震參數之間的聯合分布。共選取了七種常用的Copula函數：Independent、Gaussian、t、Gumbel、Plackett、Frank、和Clayton 函數，其中，考慮到參數c 和d 的相關性較弱的情況，在備選Copula 中加入了Independent Copula 函數，代表了參數相互獨立的情況。其余六種函數分別從不同角度描述了參數間的相關性。

圖4 給出了確定兩參數間聯合概率分布函數的步驟：

1) 計算主震與余震參數的Kendall 秩相關系數τ；

2) 由主震和余震參數的邊緣概率分布f1、f2和秩相關系數τ，求出備選Copula 函數的相關參數θ；

3) 利用BIC 作判別，遍歷七種常用Copula 函數，求得最優Copula 函數；

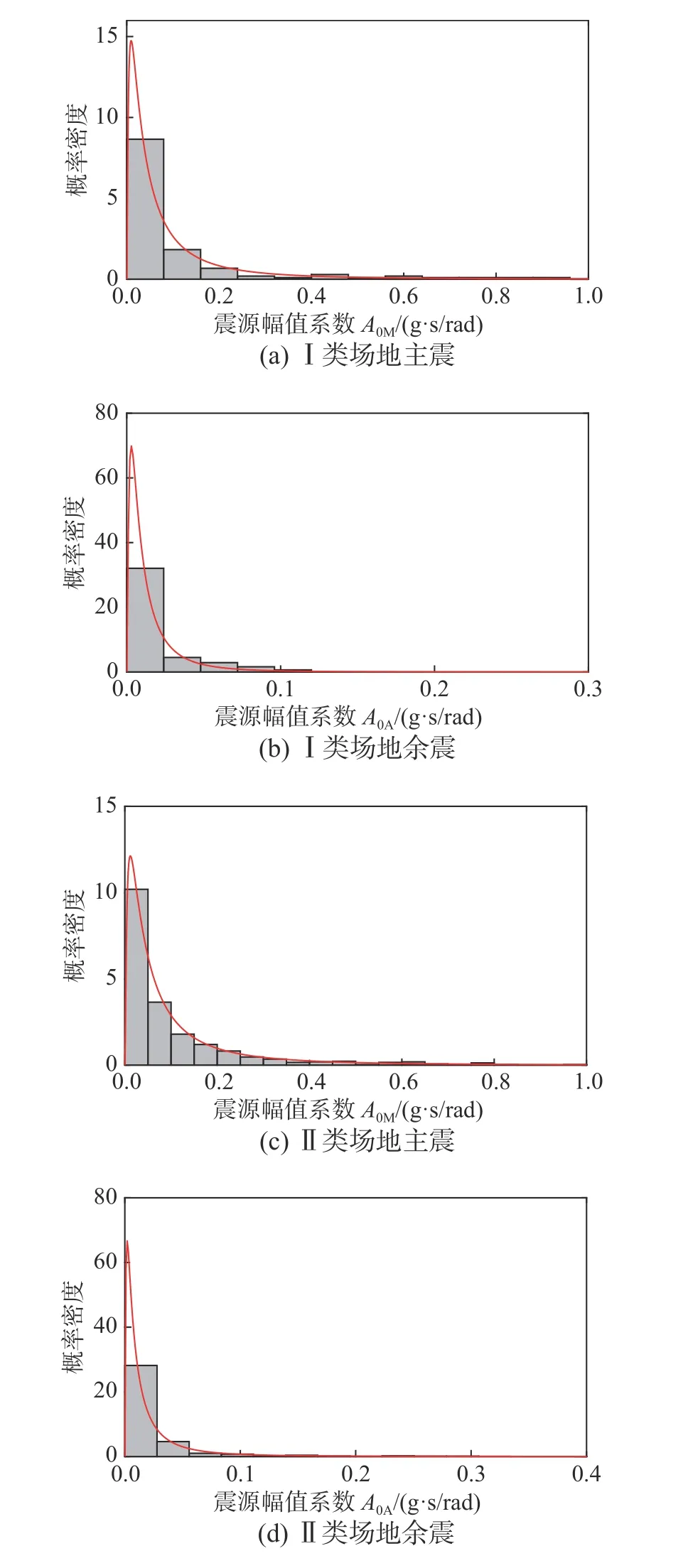
圖 2 A0M 和A0A 的邊緣概率密度函數Fig. 2 Marginal PDFs of A0M and A0A

4) 由最優Copula 函數求得主余震參數的聯合概率分布函數。

識別得到的各參數最優Copula 函數及相關參數，如表6 所示。

通過參數間的聯合PDF，本文根據等概率變換原則模擬出了符合對應聯合PDF 的散點圖。同樣以A0為例，圖5 給出了4 類不同場地條件下，參數的真實數據與模擬數據的散點圖。可見，模擬數據和真實數據的分布保持著較高的吻合度。因此，可以認為，本文利用Copula 函數得到的參數間的聯合PDF 能夠準確描述序列型地震動模型中各二維隨機變量的取值和分布，即能夠較好地描述主震和余震參數的相關性。

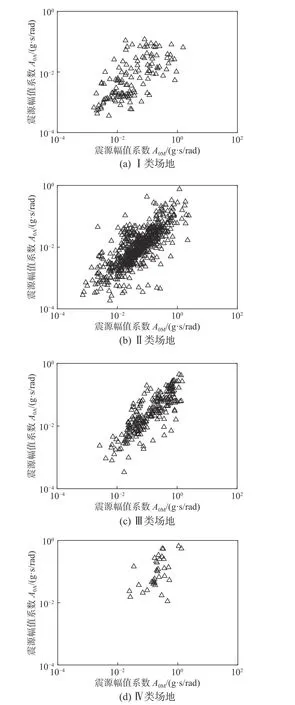
圖 3 A0M 和 A0A 的散點圖Fig. 3 Scatters of A0M and A0A

圖 4 識別最優Copula 函數的流程圖Fig. 4 Flowchart for identifying optimal Copula function

表 6 最優Copula 函數及相關參數Table 6 Optimal Copula functions and relevant parameters

圖 5 實測數據與模擬數據對比Fig. 5 Comparisons of real data and simulation

4 序列型地震動的驗證

為驗證序列型地震動模型的有效性，對實測的主余震地震動加速度時程進行模擬重構，并與實測地震動的均值反應譜進行對比驗證。另外，選取了2018 年阿拉斯加地震記錄到的地震動時程，對其進行模擬重構，進一步驗證本文模型的合理性。

首先，對每條實測的地震動時程樣本，通過式(5)識別出模型的各參數，再進行重構，最后得出模擬地震動。圖6 對比了各類場地條件下主震和余震的均值加速度反應譜，阻尼比ξ=0.05。模型與實測地震動的均值加速度反應譜基本吻合，可見式(5)模型與表4～表6 的統計結果具有較高的可信度。

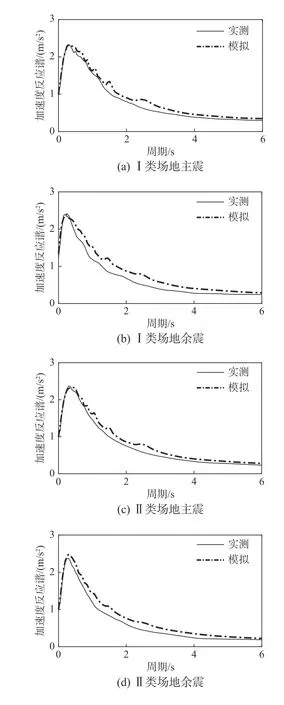
圖 6 實測地震動與模擬地震動的均值反應譜對比Fig. 6 Comparisons of mean spectra of measured and simulated records

2018 年阿拉斯加地震發生于 2018 年 11 月30 日，其中，主震震級為Mw 7.0，余震震級為Mw 5.7。本文選取了AKK217 和AKK220 測站測得的序列型地震動，分別識別出主震和余震參數，依據式(5)進行重構，結果如圖7 所示。對比可見，序列型地震動模型從樣本時程的角度能和實測時程保持較高的一致性，可以較好地重構地震動時程。需要指出，模擬時程并不能很好地描述地震動的衰減階段，衰減段持續時間較短，這是模型需要改進之處。

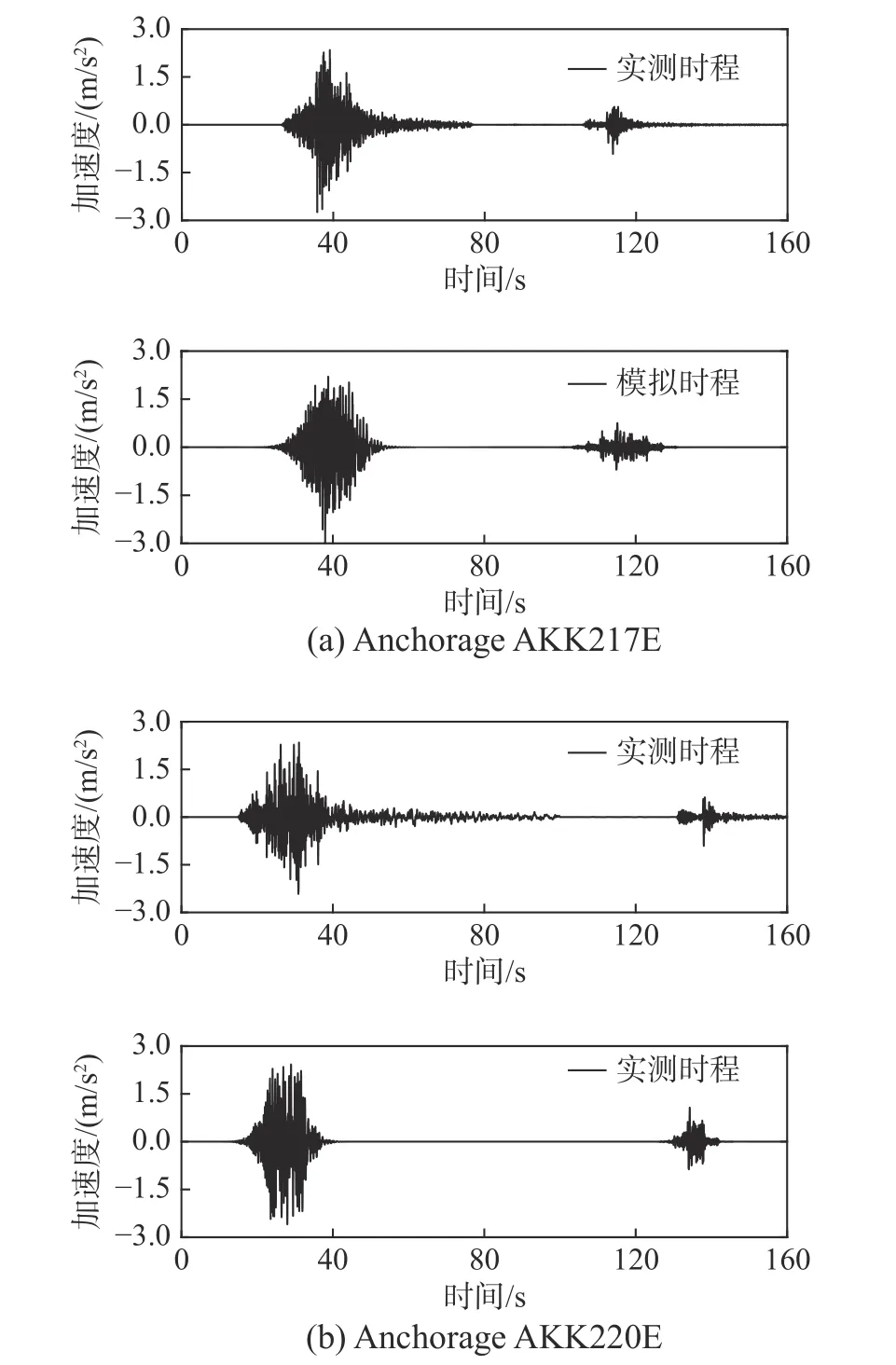
圖 7 實測單點時程與模擬時程的對比Fig. 7 Comparisons of measured and simulated records

此外，本文通過對SMART-1 臺陣的實測時程作模擬，驗證地震動場模型的合理性，選取了Event 5 地震動事件中C00 測站和I06 測站的實測加速度時程，記錄的加速度時程如圖8(a)所示。地震動在局部場地傳播過程中，地震波傳播速度是有限的，因此不同測站記錄到的地震動存在著相位差，在時程上表現為時間延遲現象。

本文首先通過式(9)識別得到Event 5 地震的物理參數，并模擬出SMART-1 局部場地原點即C00 的地震動時程。進而利用識別得到的物理參數，以及表5 中的α0和cg，模擬出沿傳播方向與C00 的Δrl為190 m 的I06 測站時程。需要說明，模擬時程中，除α0和cg外，其余物理參數都相同。模擬結果如圖8(b)所示。對比模擬得到的時程可見，其呈現出與實測時程相似的時間延遲現象。

圖 8 實測臺陣時程與場模型模擬時程對比Fig. 8 Comparisons of measured and simulated records

5 結論

通過考慮主震和余震的空間相關性，建立了序列型地震動隨機單點模型，為反映地震動在局部場地的變異性，進一步地提出了序列型地震動隨機場模型。利用1038 組序列型地震動的數據，識別得到了模型中各物理參數的統計分布。運用Copula 理論給出了主震和余震空間相關性的顯式表達。通過將模擬地震動與實測單點地震動、地震動場作對比，驗證了本文提出的模型的可行性。

模型將主震和余震的關系以概率分布的形式給出，并且在已知主震的情況下可以根據Copula理論得到余震參數的條件概率分布，保留了余震自身的隨機性。

在實際應用中，確定工程場地條件后，從表4～表6 中確定各參數的邊緣概率分布和Copula 函數確定參數的聯合概率分布，據此生成各參數的隨機樣本，代入式(5)或式(9)中，即可模擬出序列型地震動，應用于單體建筑或區域性建筑群的抗震分析。

地震動的產生與傳播過程極其復雜，如何準確描述地震的震源及傳播途徑一直是地震動建模的重點和難點。地震產生的機理復雜，傳播途徑中的影響地震動傳播的因素較多，本文提出的模型在描述地震震源及傳播途徑方面做了較多簡化；模型模擬出的時程在衰減段與實測時程有一定差異；另外，地震動在局部場地上的傳播仍有其他影響因素，本文在此也作了一定簡化，僅考慮了其行波效應。這些不足之處仍有待進一步研究。