聚焦培養(yǎng)反思習(xí)慣 助推提升核心素養(yǎng)
溫 勇
(江蘇省揚州市江都區(qū)一中 225200)
隨著新一輪的普通高中新課程改革,讓學(xué)生通過數(shù)學(xué)學(xué)習(xí)獲得數(shù)學(xué)核心素養(yǎng)的提升是數(shù)學(xué)教師應(yīng)該思考的課題,以什么樣的方式和立足點提升更是我們應(yīng)該探索和討論的話題.下面我結(jié)合兩個教學(xué)案例分析學(xué)生在解題過程中的思維活動談?wù)勛约旱母邢?
一、例題
例1已知函數(shù)f(x)=x+a2/x,g(x)=x+lnx,其中a>0.
(1)若x=1是函數(shù)h(x)=f(x)+g(x)的極值點,求實數(shù)a的值.
(2)若對任意的x1,x2∈[1,e]都有f(x1)≥g(x2)成立,求實數(shù)a的取值范圍.
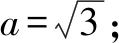
例2設(shè)函數(shù)f(x)=a2lnx-x2+ax(a>0)
(1)求f(x)的單調(diào)區(qū)間;
(2)求所有使e-1≤f(x)≤e2對x∈[1,e]恒成立的a的值.
分析第(1)問過程略,答案為f(x)的單調(diào)遞增區(qū)間為(0,a),單調(diào)遞減區(qū)間為(a,+∞).對于第(2)問思路比較清晰,求出f(x)在區(qū)間[1,e]上的值域,滿足值域為[e-1,e2]的子集.學(xué)生在求f(x)在區(qū)間[1,e]上的值域時,都是按照自然的想法對a進行分類討論,分為0 數(shù)學(xué)核心素養(yǎng)來自于學(xué)生的思考、質(zhì)疑.“反思”是重要的思維活動,是思維活動的核心和動力.反思能讓學(xué)生發(fā)現(xiàn)自己采用的解題策略和計算進程是否正確,如果在反思過程中學(xué)生發(fā)現(xiàn)無法解釋自已執(zhí)行計劃過程的意義,那么他們就會發(fā)現(xiàn)自已解題過程中的錯誤.華東師范大學(xué)教授徐斌艷等主編的《數(shù)學(xué)能力核心研究》一書中參考一系列國際性評價項目對能力認知水平的劃分,將反思與拓展列為水平三.而培養(yǎng)學(xué)生解決數(shù)學(xué)問題的能力又是數(shù)學(xué)教育的核心.波利亞將成功的問題解決者的思維過程分成四個階段,且四個階段經(jīng)常會交叉出現(xiàn).解題者一直處在制訂計劃、執(zhí)行計劃,不斷驗證,遇到錯誤及時反思并修正計劃的循環(huán)往復(fù)中.由此可見:數(shù)學(xué)問題解決能力對學(xué)生的一個重要的要求,即學(xué)生要能夠反思和再應(yīng)用.華東師范大學(xué)教授徐斌艷等主編的《數(shù)學(xué)能力核心研究》研究表明,大多數(shù)學(xué)生普遍缺乏反思,學(xué)生反思思維存在欠缺是影響學(xué)生數(shù)學(xué)核心能力提升的一個重要因素. 反思性思維是指為了獲得深層次的認識,學(xué)生主動深入地對已有數(shù)學(xué)觀點和數(shù)學(xué)思維持續(xù)進行嚴密的再思考,它是一種高層次思維,不是簡單的感知、記憶、復(fù)述或應(yīng)用,而是圍繞特定目標、通過持續(xù)性心理努力,包含發(fā)散和反思等認知活動的復(fù)雜思維.反思性思維能夠幫助學(xué)生比較、評價并糾正對問題本質(zhì)的理解,選擇最優(yōu)表達載體,使問題解決過程進一步合理完整、簡潔和諧.近年來各地高考數(shù)學(xué)試卷強調(diào)了數(shù)學(xué)核心素養(yǎng)的考查,尤其是學(xué)生的理性思維.如2018年高考全國卷Ⅱ第21題 已知函數(shù)f(x)=(2+x+ax2)ln(1+x)-2x. (1)若a=0,證明:當-1 (2)若x=0是f(x)的極大值點,求a. 教師引導(dǎo)學(xué)生用數(shù)學(xué)的思維方式進行思考比讓學(xué)生學(xué)會數(shù)學(xué)知識更重要.當學(xué)生一旦遇到新情況新問題,能夠及時將自己頭腦中的認知重新調(diào)整和整合,對情境中的信息、解決問題的過程中的重新提取,迅速抓住問題的實質(zhì),并創(chuàng)造性地解決相應(yīng)問題,在數(shù)學(xué)活動中通過對數(shù)學(xué)知識的親自探索和發(fā)展,養(yǎng)成學(xué)生反思的習(xí)慣,促進學(xué)生數(shù)學(xué)核心能力的提升,使核心素養(yǎng)真正落地生根. 1.在數(shù)學(xué)推理與論證中加強反思性思維訓(xùn)練 如果數(shù)學(xué)教學(xué)沒有創(chuàng)設(shè)反思性思維訓(xùn)練的環(huán)境,依賴學(xué)生自主學(xué)習(xí)是無法系統(tǒng)發(fā)展反思性思維的.在數(shù)學(xué)推理與論證中,自主學(xué)習(xí)、獨立思考是關(guān)鍵,但反思能領(lǐng)悟推理的實質(zhì).因此,在推理和論證過程中教師應(yīng)要求學(xué)生首先整理思維過程,確定關(guān)鍵點,使推理的思維過程精細化、概括化;其次通過反思證題方法技巧,領(lǐng)悟數(shù)學(xué)思想方法;再次重新剖析推理與論證的本質(zhì),逐漸深化推理,提高思維的抽象性;最后還要引導(dǎo)學(xué)生比較推理與論證方法的優(yōu)劣,進一步優(yōu)化推理與論證過程,得出解決問題的最佳方案. 2.在數(shù)學(xué)教學(xué)過程中加強反思性數(shù)學(xué)學(xué)習(xí) 現(xiàn)代數(shù)學(xué)觀已經(jīng)由靜態(tài)、絕對主義的數(shù)學(xué)觀轉(zhuǎn)變?yōu)閯討B(tài)、經(jīng)驗的數(shù)學(xué)觀,數(shù)學(xué)學(xué)習(xí)不是面對封閉、僵化的數(shù)學(xué)公式和原理,而是在數(shù)學(xué)活動中進行體驗、探索和創(chuàng)造的過程.而教師在數(shù)學(xué)教學(xué)中要有意識的給予學(xué)生充分的機會去反思并表達,比如鼓勵學(xué)生提問、評價同伴的觀點,或示錯教學(xué),讓學(xué)生針對自身的思考過程、解題思路、運算過程或推理邏輯等進行積極的再思考. “授之以魚,不如授之以漁”,以數(shù)學(xué)學(xué)習(xí)的過程中,關(guān)注數(shù)學(xué)反思,有意識的培養(yǎng)學(xué)生及時反思的習(xí)慣,提升學(xué)生的核心素養(yǎng).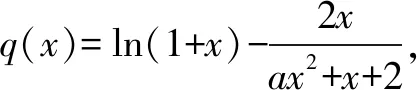
二、建議

