精解·探規·尋根·遷移：數學教師研題的四重境界*

曾 榮

習題是課堂教學內容的鞏固與深化，應當為學生發展數學學科核心素養提供助力。優質的數學習題教學，有利于幫助學生理解數學知識的本質，感悟數學的基本思想，積累數學思維的經驗，提升數學學科核心素養。研究習題是高中數學教師的基本教學任務，也是他們的必備素養與能力。筆者認為，教師研究習題，不能局限于會解、能講，而應該依托優秀的試題，追求更高境界——多思精解、探求規律、探尋題根、有效遷移。教師研題的基本模式如圖1所示。本文結合江蘇省南通市2020年高三第一次模擬考試第17 題談談教師研題的四重境界。

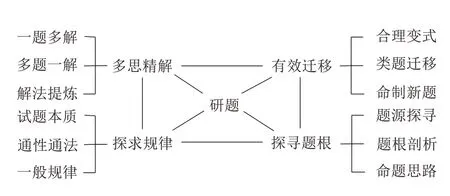
圖1 研題模式

一、第一重境界：多思精解，比較不同解法的效率差異

教師研題的基礎是解題，用合適的方法、廣闊的思維進行解題，要善于進行一題多解、多題一解、解法提煉。一道優秀的試題往往講究解法的多樣性和不同解法效率的差異性，這種差異性體現出解題人思維品質和數學素養的差

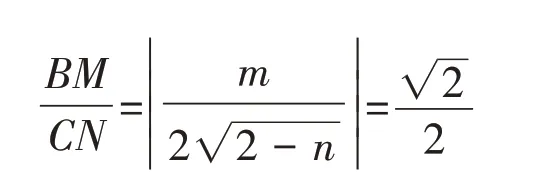
【比較反思】以上幾種方法是解析幾何中的常見解法，但不同解法的效率有明顯差異。在同一數學情境中，不同的運算思路、運算程序的設定，體現了一定的規劃設計能力。對于具體的數學運算，我們要善于結合運算情境，深刻理解運算對象的特征，挖掘其內涵。只有以數學思維為基礎進行規劃設計，運算能力的提升才能得到有效的落實。

二、第二重境界：探求規律，理解試題內在的本質屬性

多思精解，深入比較不同解法的效益差異，可以幫助師生優化解題路徑，提升學科素養。同時，我們應該依托試題，探求其內在規律，理解試題內在的本質屬性。在深入研究多種解法的基礎上，我們應進一步思考，問題背后的知識本質是怎樣的？解題方法蘊含著怎樣的通性通法、數學思想？是否存在更一般的規律？為什么會有這樣的規律？對題1，我們進行如下思考：

【思考1】題1依托矩形這一背景，研究了與橢圓有關的問題。第①問是給定了兩個特殊的分點，研究了對應的直線的交點在橢圓上。如果不是中點，而是三等分點、四等分點，……，n等分點呢？有沒有更一般的結論呢？

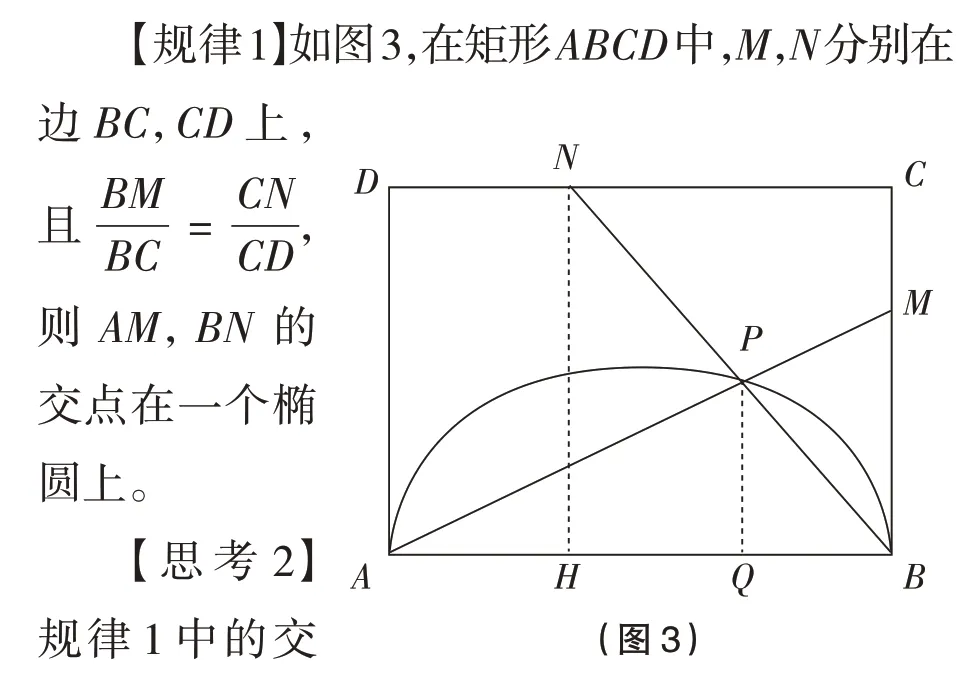
三、第三重境界：探尋題根，挖掘試題背后的命題思路

對于一道試題，教師若能多思精解、由特殊到一般、把握本質屬性、研透內在規律，已屬不易。然而，優秀的教師往往不止于此，他們會研究問題出處，探尋題根，并深刻挖掘基于題根的命題思路。這種基于“問題從哪里來？怎么演變過來的？命題者的命題思路和方法是怎樣的？”的思考，力求站在命題者的視角審視問題，求本歸真，更有利于提升師生的數學學科素養。本題題根如下——

題2（蘇教版高中數學選修2-1 P38 第14題）：把矩形的各邊n 等分，如圖6 連結直線，判斷對應直線的交點是否在一個橢圓上？

【題根分析】本題依托矩形這個載體，通過等分的方式產生了有限個點。等分的實質是“成比例”，通過“成比例”可以將“有限”轉化為“無限”，由此進一步通過對應直線相交的方式產生的無數個點。研究這些點的特征，實質上是研究動點的軌跡問題。

【命題思路】在高考、模考中如果直接考查軌跡問題，那么對學生的學習要求高、難度大。為了讓問題能更加適合于考查學生，命題者通過“特殊化”和“逆向思考”的方式改變了問題的呈現方式，使試題源于教材，但不拘泥于教材。

（1）特殊化：在題1 第①問中，命題者將分點特殊化，取其中一個特殊的分點進行研究。因為只取了一個點，就不再是對軌跡問題的研究了。命題者結合具體數據，給出特殊的橢圓，將求橢圓軌跡問題轉化為求在特定橢圓上的特殊點。這樣，動態問題轉化為靜態問題，大幅度降低了難度，適合用于考查學生。

（2）逆向思考：滿足某一特征的點在曲線上，曲線上的點都滿足某一特征，這是解析幾何研究的兩個主要問題。題1 第①問研究的目標是點在曲線上。命題者在命制第②問時，通過逆向思考，告知曲線上的一個動點，進而研究相關點的幾何特征。在這個“動”的情境中，可以通過不同的引參方案，考查學生的思維能力和數學運算素養。

四、第四重境界：有效遷移，開發試題蘊含的教學價值

教師研題不僅僅是為了提升自身的數學素養，更重要的是為了開發試題蘊含的教學價值，幫助學生提高數學解題能力，加深對數學的理解。教師將自己解題、探規、尋根的經歷轉化為一種探究活動，可以幫助學生實現對問題的再發現、再解決。同時，在教學中，教師還要善于有效遷移，對試題進行改編、變式、拓展，舉一反三，讓學生在遷移、深化中體悟數學的本質和數學的系統性、結構性，感悟數學的統一之美、變化之美。

遷移1（蘇教版高中數學選修2-1 P48第16題）：如圖7，在矩形ABB'A'中，把邊AB分成n等份。在邊B'B 的延長線上，以BB'的n 分之一為單位連續取點。過邊AB 上各個分點和A'作直線，過B'B 延長線上的對應分點和點A 作直線，這兩條直線的交點為P，P在什么曲線上運動？

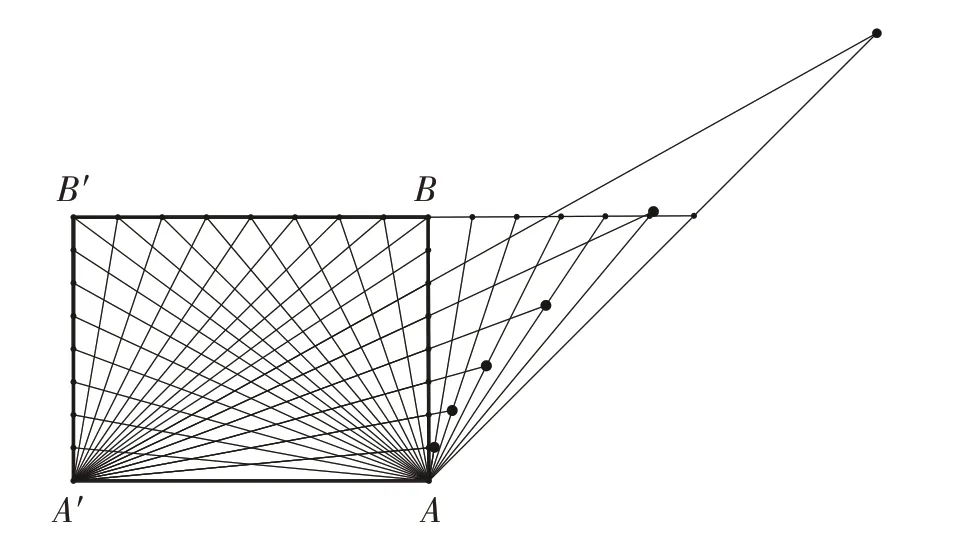
（圖7）

遷移2（蘇教版高中數學選修2-1 P54 第13 題）：（閱讀題）在工程中，畫拱寬為2a，拱高為h的拋物線，常用下面的畫法：

（1）作矩形ABCD，使AB=2a，DA=h；

（2）分別取CD，AB的中點O，H，把線段DA，OD，HA各n等分；

（3）如圖8 連線得到各交點，將交點連成光滑曲線，就得到拋物線的一半；

（4）用同樣方法畫出另一半。

你能說明上述畫法的正確性嗎？

對于以上問題，我們要在外在形式、結構的一致性的基礎上，深刻認識本質的一致性。

【思考1】你能研透上述題2、遷移1、遷移2的本質一致性嗎？（橢圓、雙曲線、拋物線統稱為圓錐曲線。圓錐曲線在定義的方式、知識的結構、研究的方法等方面具有一致性。設計這樣的問題，意在引領學生舉一反三，由表及里，深刻認識圓錐曲線的本質。）

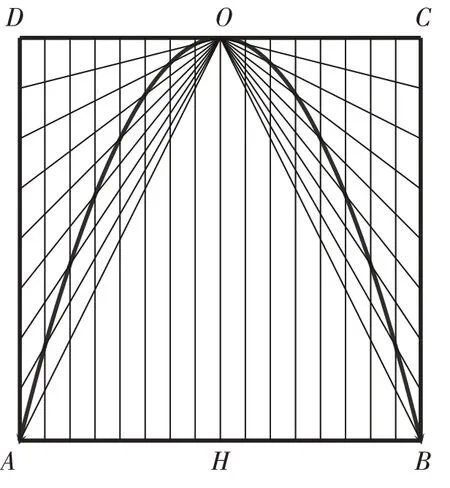
（圖8）

【思考2】你能參考題1的改編方式，將遷移1、遷移2 改編成形如題1 的考題嗎？（在深刻認識問題本質的同時，教師也要學會“再創造”，借鑒優秀試題的命制方式，“再創造”出更多的優秀試題，讓學生有機會再練、再悟、再提高。）

數學家波利亞曾指出：“解題是人類最富有特征的一種智力活動。”作為數學教育工作者，我們不能僅僅滿足于一般意義上的解題，我們要善于深度研題。通過“多思精解—探求規律—探尋題根—有效遷移”的路徑，使得研題活動助力教師的專業成長，助力智慧課堂的有效達成，也助力促進學生核心素養的不斷提升。