對數變換主成分分析的圖像識別
宋昱,孫文赟,陳昌盛
(1.深圳大學電子與信息工程學院,518060,廣東深圳;2.深圳大學深圳市媒體信息內容安全重點實驗室,518060,廣東深圳;3.深圳大學廣東省智能信號處理重點實驗室,518060,廣東深圳)
主成分分析(PCA)[1]是一種線性變換算法,在圖像處理和機器學習中有很多重要的應用。PCA將高維數據投影至低維空間,可以有效地表示高維數據。然而,PCA也有一些缺點。因為PCA采用l2范數的平方衡量原樣本與重構樣本的誤差,所以當數據中有些樣本明顯遠離其他樣本,即數據中含有異常樣本時,這些異常樣本會對PCA的目標函數造成顯著的影響[2-5],從而導致標準PCA不能很好地處理含有異常樣本的數據。
為了減小異常樣本帶來的負面效果,研究者提出了很多魯棒PCA算法。文獻[6]和文獻[7]通過對樣本進行最大似然估計,得到了基于l1范數的PCA算法。文獻[6]采用啟發式的估計算法檢測異常樣本,文獻[7]采用凸優化算法檢測異常樣本。文獻[8]采用非凸M估計算子作為目標函數,學習得到彩色圖像的表示。盡管這些算法具有對異常樣本的魯棒性,但是有一個共同的缺點,即不具有旋轉不變性,而旋轉不變性是學習算法應具有的一個重要性質[9]。為了保留標準PCA算法的旋轉不變性,研究者提出了一些魯棒的旋轉不變PCA算法[3-4,10-13]。文獻[10]提出了PCA-L1,采用貪婪算法最大化投影后樣本的l1范數。文獻[11]提出了一種非貪婪算法,以此求解PCA-L1的目標函數,可以同時求解所有的投影方向。為了擴展PCA-L1算法,文獻[12]提出了PCA-Lp算法,該算法最大化投影后樣本的lp范數。PCA-L1或者PCA-Lp并沒有最小化重構誤差,而是最大化投影后樣本的l1或者lp范數,其目標函數與標準PCA的目標函數有本質不同。文獻[3]和文獻[4]提出了R1-PCA,其目標函數中使用了2種范數,在樣本空間維度上使用了l2范數,在樣本間使用了l1范數。文獻[13]提出了Φ-PCA,其目標函數是一個二階可導的凸函數,可以采用牛頓迭代法求解。然而,R1-PCA和Φ-PCA假設數據是均值的,該假設在實際中有一定的限制[14]。為了估計樣本均值,文獻[15]提出了基于最大相關熵的PCA。為了進一步擴展R1-PCA,文獻[16]提出了基于l2,p范數的PCA。該算法采用l2,p范數衡量原樣本與重構樣本的誤差,當p=1時,該算法與R1-PCA算法等價。
盡管研究者已經提出了眾多的魯棒PCA算法,但是這些算法在處理含有異常樣本的數據時依然有一些不足。以基于l2,p范數的PCA算法為例,不能在理論上保證該算法的目標函數值小于標準PCA算法的,從而其處理異常樣本的性能不能得到保證。為了改進現有的魯棒PCA算法,本文提出了一種基于對數變換的魯棒PCA算法,可以在理論上證明所提算法的目標函數值小于標準PCA算法的,從而提高現有魯棒PCA算法處理含有異常樣本數據的能力。所提算法保留了標準PCA算法的性質,即具有旋轉不變性,且投影矩陣與數據協方差矩陣相關。實際數據集上的實驗結果證明了所提算法的有效性。
1 標準PCA算法和魯棒PCA算法
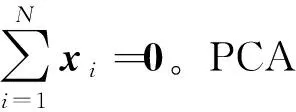
(1)
式中Ik是k×k的單位矩陣。通過代數運算,可以得出目標函數式(1)等價于
(2)
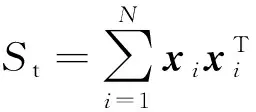
從目標函數式(1)可以看出,PCA在平方的意義上最小化重構誤差,使得目標函數對于異常樣本非常敏感[3-5]。異常樣本重構誤差的平方非常大,對于目標函數有顯著影響,會影響得到的投影矩陣。為此,研究者提出了很多魯棒PCA算法,例如基于l1范數的PCA算法[11-12],該算法的目標函數為
(3)
基于l1范數的PCA算法通過求解目標函數式(3)得到投影矩陣。目標函數式(3)的解與協方差矩陣的關系并不清楚,而且因為‖xi-WWTxi‖1+‖WTxi‖1≠‖xi‖1,目標函數式(3)并沒有最小化重構誤差。PCA算法的目標函數最小化了重構誤差,這說明目標函數式(3)與PCA算法的目標函數有本質不同。目標函數式(3)的解不等價于
(4)
目標函數式(4)直接考慮了數據的重構誤差,并且對異常樣本具有一定的魯棒性。然而,目標函數式(4)不容易求解,其求解算法的計算量很大[3],而且目標函數式(4)不具有旋轉不變性。為了改進基于l1范數的PCA算法,文獻[16]中提出了基于l2,p范數的PCA算法,其目標函數為
(5)
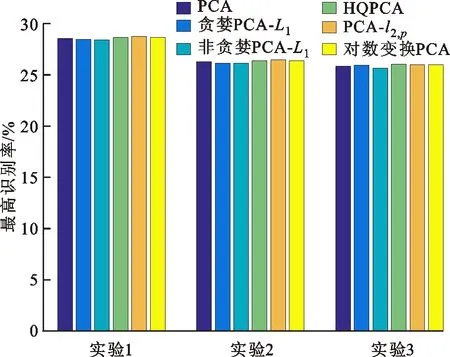
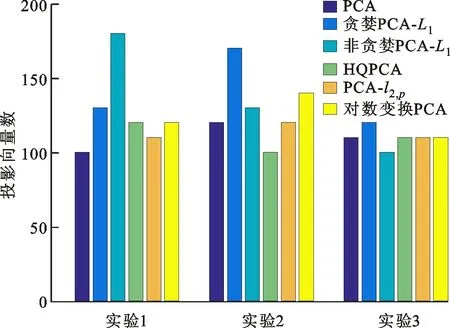
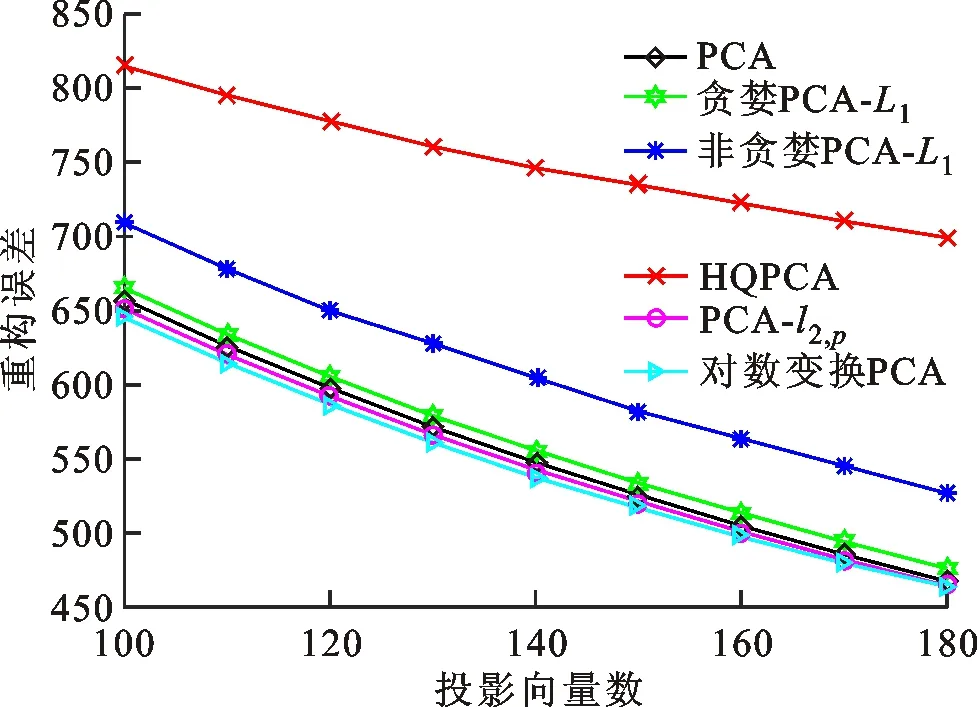
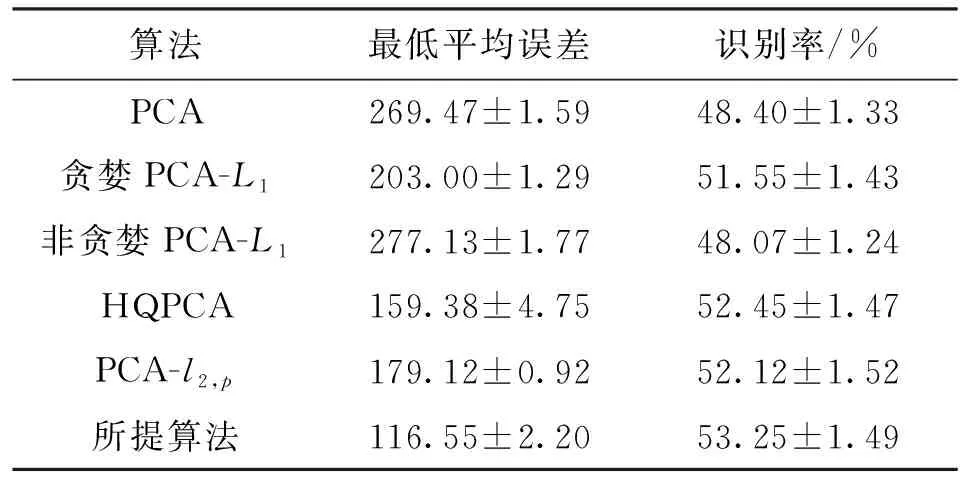
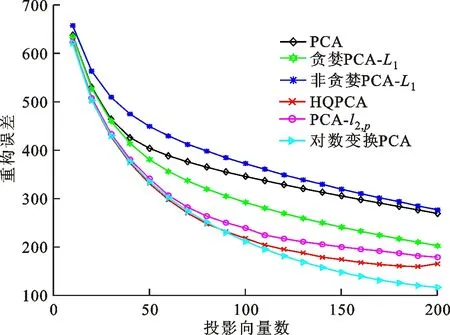
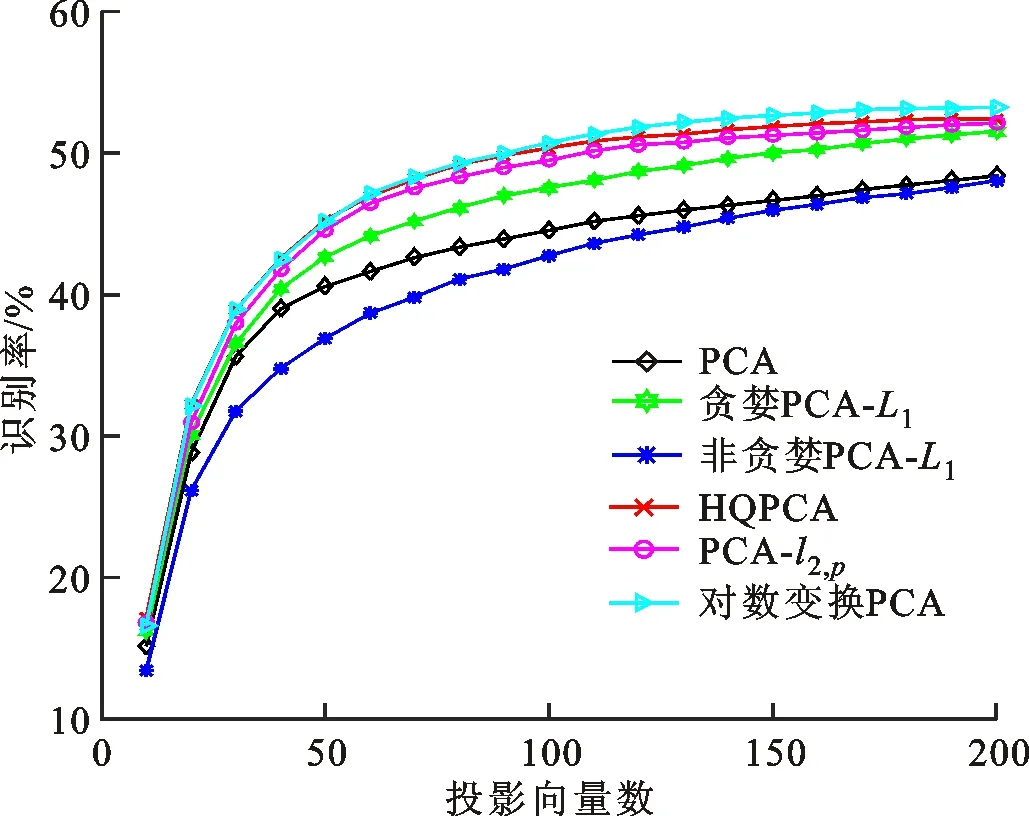
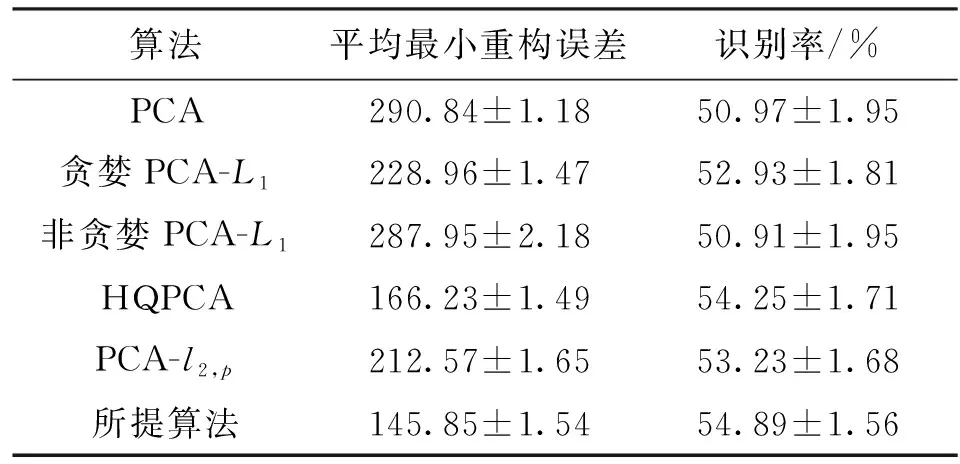
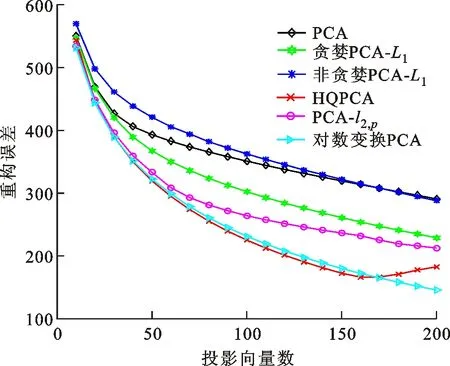
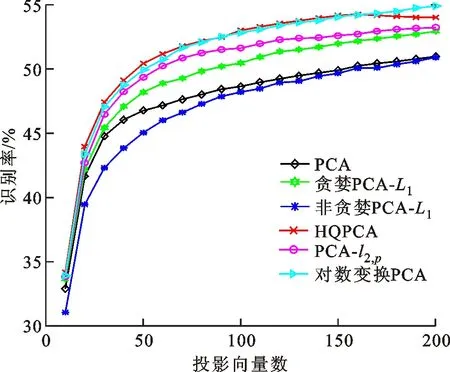
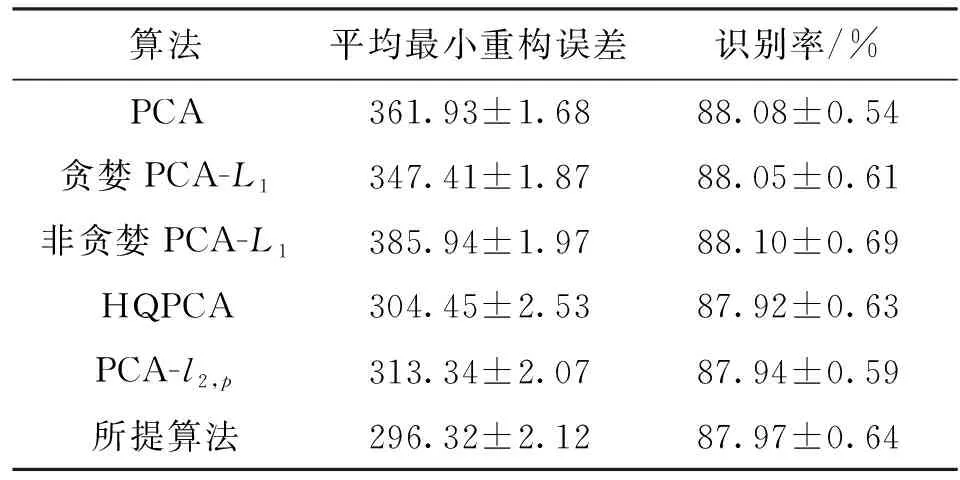
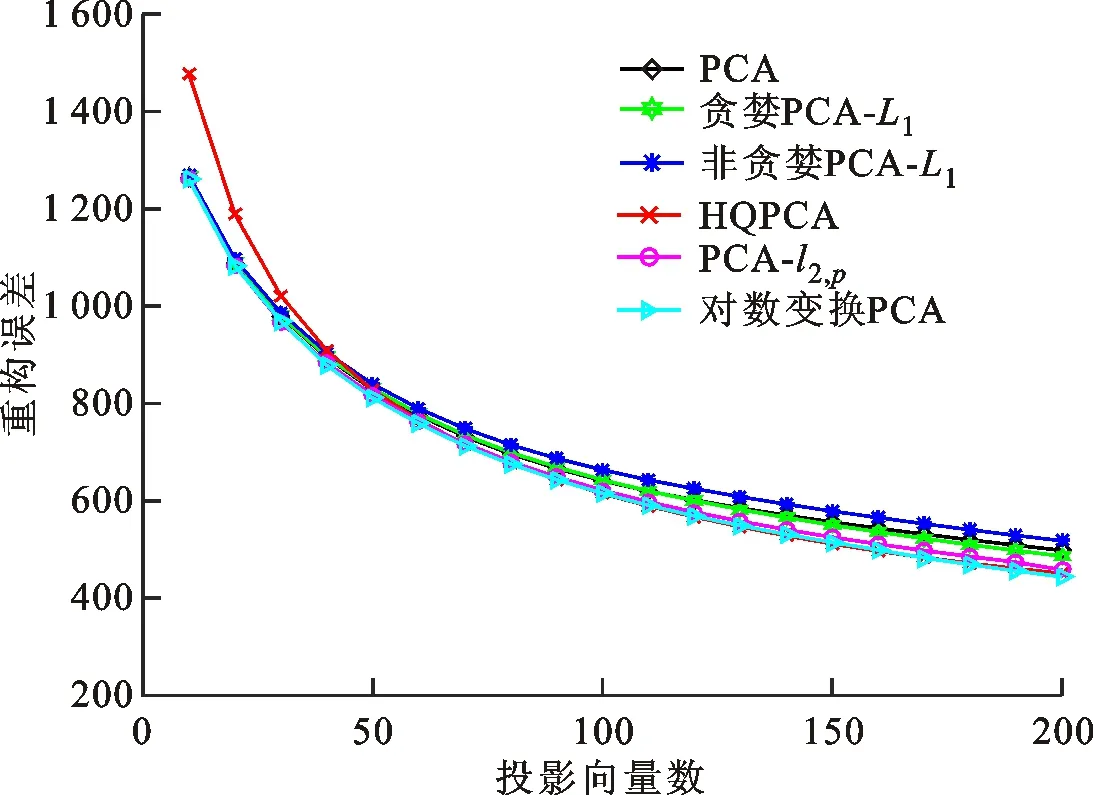
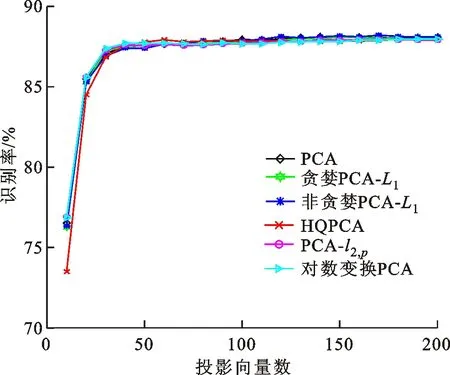
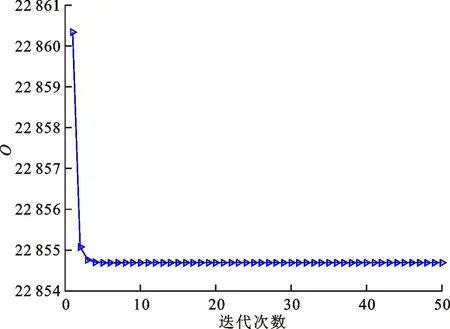
式中0 為了從理論上保證所提算法的目標函數值小于目標函數式(1)的,采用對數形式。當x≥0時,有 x≥ln(x+1) (6) (7) 進一步得到 (8) 這樣就從理論上保證了重構誤差的減小,而不等式(8)的右側即為本文采用的目標函數,即 (9) 通過代數運算,可以得到 (10) (11) (12) 式中D是一個對角矩陣,其對角線上的元素是di。根據矩陣理論,目標函數式(12)中W*的列向量應是對應于矩陣XDXT最大的k個特征值的特征向量。求解出矩陣W后,再更新di。重復上述迭代過程直至收斂,收斂條件為 (13) 式中:Ot和Ot-1分別表示在第t次和第t+1次目標函數式(9)的取值;ε是一個小的常數,取為10-3。 求解目標函數式(9)的優化算法為對數變換的PCA,即算法1,偽代碼如下。 輸入:X=[x1,…,xN]∈Rd×N,k while 不收斂 do 1.計算對角矩陣D,其對角線上的元素為 2.計算加權協方差矩陣XDXT 4.t=t+1 end while 輸出:Wt∈Rd×k 定理1在算法1的每一次迭代中,有 (14) 證明根據算法1,在第t+1次迭代時,有 (15) (16) (17) (18) (19) (20) 對數函數ln(·)是凹函數,滿足式(20),即 (21) (22) 結合不等式(19),可以得到不等式(22)的右側小于0,所以可得 (23) 定理2算法1近似收斂于目標函數式(9)的最優解處。 證明目標函數式(9)是約束優化問題。采用拉格朗日乘子法,將其轉換為非約束優化問題。目標函數式(9)對應的拉格朗日函數為 tr(ΛT(WTW-I)) (24) 式中Λ是拉格朗日乘子。為了滿足約束條件WTW=Ik,Λ應設為對角矩陣。根據KKT條件,在最優解處有dL=0。對式(24)取微分,可得 tr(WΛT(dW)T) (25) 為了使得dL=0,應滿足 (26) 目標函數式(12)的最優解在算法1的第3步得到,所以算法1收斂時的解滿足目標函數式(12)的KKT條件。目標函數式(12)的拉格朗日函數為 (27) 對L2取微分,并令其微分為0,可得 (28) 旋轉不變性意味著投影結果,即高維數據的低維表示,在樣本空間經過旋轉后保持不變。 定理3算法1的解具有旋轉不變性。 證明任意給定一個旋轉矩陣Γ(ΓTΓ=I),投影矩陣W和樣本xi的旋轉變換表示為 (29) 因為ΓTΓ=I,從而可得 (30) 將式(29)和式(30)進行結合,算法1的目標函數可以表示為 (31) (32) 樣本xi的低維表示在旋轉變換下并不改變。證畢。 圖1 重構誤差與目標函數值的關系 與現有的PCA-L1算法相比,所提的基于對數變換的PCA算法最小化重構誤差,與PCA算法的目標一致。與目標函數式(4)對應的算法相比,所提算法保留了PCA算法的旋轉不變性。與基于l2,p范數的PCA算法相比,在理論上所提算法的目標函數值小于PCA算法的,避免了l2,p范數放大較小重構誤差的缺點。所提算法具有良好的收斂性。 為了驗證所提算法的有效性,在AR、Extended Yale B和CMU PIE共3個人臉數據集及MNIST共1個手寫字符數據集上進行了實驗,和標準PCA算法[1]、貪婪求解的基于l1范數的PCA算法[10](記為貪婪PCA-L1算法)、非貪婪求解的基于l1范數的PCA算法[11](記為非貪婪PCA-L1算法)、基于最大相關熵的PCA算法[15](記為HQPCA算法)以及基于l2,p范數的PCA算法[16](記為PCA-l2,p)進行了比較。設置PCA-l2,p算法的p=1。使用最近鄰算法對降維后的數據進行分類,近鄰數取為1。投影向量數k從10取到200。重構誤差為 (33) AR數據集[17]包含126人的超過4 000幅彩色正面人臉圖像,實驗中轉為灰度圖像。實驗選擇其中119人(65名男性和54名女性)的3 094幅圖像作為數據集。這些圖像在2個時段拍攝(相隔2周)。每個時段包含13幅圖像,6幅圖像有眼鏡或圍巾遮擋,7幅圖像有不同表情和光照。從每幅圖像中選出人臉區域,并將圖像大小調整為50×40像素[18]。圖2是AR數據集中的某人圖像,圖像a~m來自第1個時段,圖像n~z來自第2個時段。 abcdefghijklm 在AR數據集上,進行3組實驗,實驗1是眼鏡遮擋實驗,實驗2是圍巾遮擋實驗,實驗3是眼鏡和圍巾遮擋實驗。在實驗1中,選擇每人10幅圖像,即圖像a~j作為訓練樣本,圖像n~w作為測試樣本,其中被眼鏡遮擋的圖像是異常樣本。在實驗2中,選擇每人10幅圖像,即圖像a~g和k~m作為訓練樣本,圖像n~t和x~z作為測試樣本,其中被圍巾遮擋的圖像是異常樣本。在實驗3中,選擇每人13幅圖像,包括第1個時段的13幅圖像a~m作為訓練樣本,其他圖像作為測試樣本,被眼鏡或者圍巾遮擋的圖像是異常樣本。 圖3是AR數據集上的平均重構誤差和最高識別率。從圖3a可以看出:在實驗1和2中,所提算法的重構誤差與PCA-l2,p算法的接近,2種算法的重構誤差小于其他4種算法的;在實驗3中,所提算法的重構誤差最小,優于其他算法的;在所有實驗中,HQPCA算法的重構誤差明顯高于其他算法的。從圖3b可以看出,所提算法和HQPCA算法以及PCA-l2,p算法的識別率接近,高于其他3種算法的。 (a)平均重構誤差 (b)最高識別率圖3 AR數據集上的平均重構誤差和最高識別率 圖4是AR數據集上的性能比較。從圖4a可以看出,當投影向量數在100~180時,各算法取得最高的識別率,由此表明投影向量數在100~180變化時,對各算法有重要影響。從圖4b中可以看出,當投影向量數在100~180時:所提算法取得了最小重構誤差;PCA-l2,p算法取得了較小的重構誤差;HQPCA算法的重構誤差較大。對于AR數據集上的3類實驗,在第1、2類實驗中分別加入了被眼鏡遮擋的樣本和被圍巾遮擋的樣本作為異常樣本,異常樣本數量占的比例較小。實驗1和實驗2不能充分體現魯棒PCA算法處理含有異常樣本數據集的優越性。實驗3中加入了被眼鏡和圍巾遮擋的樣本作為異常樣本,異常樣本占比明顯高于實驗1和實驗2的。實驗3上的結果更能體現魯棒PCA算法的優越性。綜合可知,所提算法在實驗3上取得了最小的重構誤差,且取得了較高的識別率。 (a)取得最高識別率時對應的投影向量數 (b)實驗3的重構誤差圖4 AR數據集上的性能比較 Extended Yale B數據集[19]包含了來自38人的2 144幅在不同光照下的圖像。在該實驗中,將人臉圖像的大小調整為32×32像素[18]。從每個人的圖像中隨機選取14幅圖像,然后隨機選取圖像的一部分,將這部分替換為含有椒鹽噪聲的圖像塊。該圖像塊只包含像素值為0和255的點,大小取為12×12像素。圖5是Extended Yale B數據集中的部分正常圖像和含噪圖像。對于每一個人,隨機選取25幅正常圖像和7幅含噪圖像作為訓練樣本,該人的其他圖像作為測試樣本。實驗重復10次。 (a)正常圖像 (b)含噪圖像圖5 Extended Yale B數據集中的部分圖像 表1是Extended Yale B數據集上各算法的最低平均重構誤差和對應的識別率,表中以“量值±標準差”的形式表示。 表1 Extended Yale B數據集上各算法的最低平均誤差和對應的識別率 圖6是Extended Yale B數據集上各算法的性能比較。從圖6和表1中可以看出:所提算法在數據重構和分類上的性能明顯優于其他5種算法的,性能僅次于所提算法的是HQPCA算法,再次是PCA-l2,p算法;HQPCA在投影向量數從190變為200時,重構誤差下降,而其他5種算法依然保持上升;PCA算法性能不佳,這是因為數據集中含有異常樣本,而異常樣本對PCA算法的重構誤差有較大影響;貪婪和非貪婪PCA-L1算法由于沒有直接最小化重構誤差,而是最大化投影后向量的l1范數,所以性能也不佳;所提算法優于PCA-l2,p算法,這是因為所提算法沒有放大小的重構誤差,對于大的重構誤差也有更大的抑制,所以所提算法取得了最優的性能。在Extended Yale B數據集上實驗結果與理論分析一致,且與AR數據集上的實驗結果一致。 (a)重構誤差和投影向量數的關系 (b)識別率和投影向量數的關系圖6 Extended Yale B數據集上各算法的性能比較 CMU PIE數據集[20]包含了來自68人的2 856幅正面人臉圖像。每人含有42幅在不同光照條件下拍攝的圖像。在該實驗中,將每幅圖像的大小調整為32×32像素[18],并且加入了類似于在Extended Yale B數據集的實驗中加入的噪聲。從每人的圖像中隨機選擇10幅圖像加入噪聲。圖7是部分CMU PIE數據集上的人臉圖像和含噪圖像。隨機選取每個人的21幅圖像(16幅正常圖像和5幅含噪圖像)作為訓練樣本,其他圖像作為測試樣本。實驗重復10次。 (a)正常圖像 (b)含噪圖像圖7 CMU PIE數據集中的部分圖像 表2是CMU PIE數據集上各算法的平均最小重構誤差和對應的識別率。 表2 CMU PIE數據集上各算法的平均最小重構誤差和對應的識別率 圖8是CMU PIE數據集上各算法的性能比較。從表2和圖8可以看出:所提算法取得了最優的性能,性能僅次于所提算法的是HQPCA算法;對于HQPCA算法,當投影向量數較小時,其性能與所提算法接近,隨著投影向量數的增加,其性能達到最優后開始變差,而所提算法的性能隨著投影向量數的增加一直增加,并且優于HQPCA算法的最優性能。在CMU PIE數據集上的實驗結果與理論分析一致,并且與在AR數據集和Extended Yale B數據集上的實驗結果一致。 (a)重構誤差和投影向量數的關系 (b)識別率和投影向量數量的關系圖8 CMU PIE數據集上各算法的性能比較 MNIST數據集[21]共包含了70 000幅手寫數字圖像,其中訓練集有60 000幅圖像,測試集有10 000幅圖像。每幅圖像的大小是28×28像素,手寫數字位于圖像中間。在本實驗中,從測試集中選取5 000幅圖像,每個字符(即0~9)包含500幅圖像。從每個字符的圖像中隨機選取120幅圖像,然后隨機選取圖像的一部分,將這部分替換為含有椒鹽噪聲的圖像塊,圖像塊的大小取為10×10像素。對于每一個字符,隨機選取190幅正常圖像和60幅含噪圖像作為訓練樣本,該字符的其他圖像為測試樣本。實驗重復10次。表3是MNIST數據集上各算法的平均最小重構誤差和對應的識別率。 表3 MNIST數據集上各算法的平均最小重構誤差和對應的識別率 圖9是MNIST數據集上是各算法的性能比較。從表4和圖9a可以看出:所提算法取得了最小的重構誤差,HQPCA算法和PCA-l2,p算法也取得了較好的性能,它們的性能都優于其他3類算法的;當投影向量數較小時,HQPCA算法的重構誤差略小于所提算法的,而當投影向量數量增大時,所提算法的性能逐漸優于HQPCA算法的。從圖9b可以看出:各算法的識別率非常接近,最高的識別率(PCA)與最低的識別率(HQPCA)之間的差距為0.16%,基本可以忽略;當投影向量數較少時,所提算法取得了最高的識別率。綜上可知,所提算法的特征提取性能優于其他對比算法的。 (a)重構誤差和投影向量數的關系 (b)識別率和投影向量數的關系圖9 MNIST數據集上各算法的性能比較 AR數據集上實驗3的目標函數值與迭代次數的關系曲線如圖10所示,投影向量數k=10。可以看出,所提算法的目標函數值迅速減小至收斂,大概在第5次迭代時即可達到收斂。圖10的結果與2.3小節中對于算法收斂性的理論分析一致,所提算法可以得到目標函數的最優解。 圖10 所提算法目標函數值與迭代次數的關系曲線 本文提出了一種魯棒PCA算法——基于對數變換的PCA算法。從對數變換的性質出發,導出了所提算法使用的目標函數。所提算法的目標函數值和標準PCA算法的呈對數變換關系,從理論上保證了所提算法的目標函數值小于標準PCA算法的。因為對標準PCA算法的目標函數采用了對數變換,大幅降低了異常樣本對于目標函數值的影響,從而保證了所提算法的魯棒性。理論分析表明,所提算法的每次迭代可以近似降低目標函數值,并且可以近似收斂于目標函數的最優解。 人臉數據集和手寫字符數據集上的實驗充分表明了所提算法的優越性。與現有的魯棒PCA算法相比,所提算法對于異常樣本的魯棒性和處理能力有較大提升,取得了最低的重構誤差并且取得了最高的識別率。與PCA-l2,p算法相比,所提算法的目標函數能夠降低較小的重構誤差,同時對于較大的重構誤差有更強的抑制。與PCA-L1算法相比,所提算法保留了PCA算法具有的旋轉不變性。實驗分析表明,所提算法的收斂性能較好,一般迭代數次即可收斂,與理論分析一致。 未來可將對數變換應用于稀疏PCA算法,從而得到能更好地處理含有異常樣本的稀疏PCA算法。2 對數變換的PCA算法
2.1 目標函數建立
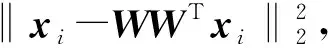
2.2 目標函數求解
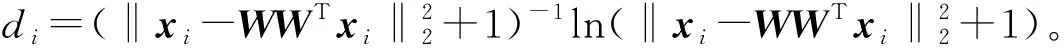
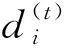
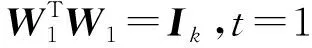
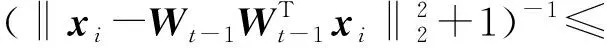
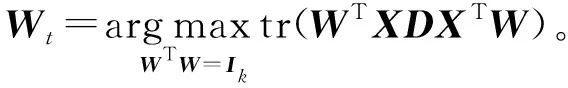
2.3 收斂性分析
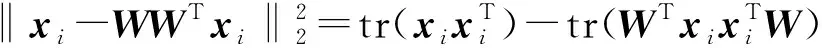
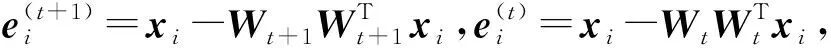
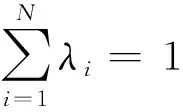
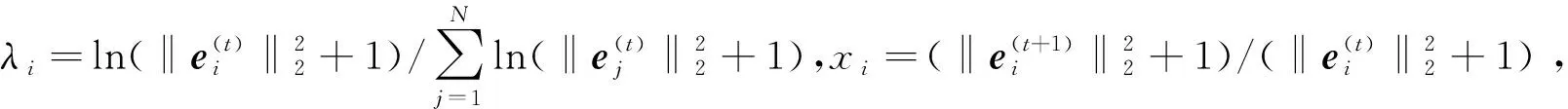
2.4 旋轉不變性分析
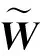
3 實驗結果與分析
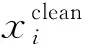
3.1 在AR數據集上的實驗

3.2 在Extended Yale B數據集上的實驗


3.3 在CMU PIE數據集上的實驗


3.4 在MNIST數據集上的實驗
3.5 收斂性實驗
4 結 論

