燃氣發電鍋爐主汽壓滑模預測優化控制策略

章家巖,王勝,馮旭剛,鮑立昌,魏舜昊,陳雨薇,徐帥

(安徽工業大學電氣與信息工程學院,243032,安徽馬鞍山)

主汽壓是衡量發電鍋爐蒸汽產量與負荷是否匹配的重要指標,反映了鍋爐燃燒過程的能量平衡狀態。鍋爐燃燒控制系統的主要任務是根據汽輪機負荷來調整燃料供應量,從而達到保持主汽壓穩定的目的[1-2]。煉鐵和煉鋼生產過程中產生的高爐煤氣和轉爐煤氣是冶金企業自備電廠燃氣發電鍋爐的燃料。由于高爐煤氣和轉爐煤氣壓力和熱值波動較大,所以燃氣發電鍋爐主汽壓難以控制穩定,這將給發電機組的安全穩定運行帶來嚴重的隱患[3-4]。

工程上針對鍋爐主汽壓通常采用常規的PID控制方法,難以達到理想的控制效果。為此,國內外專家學者進行了先進控制策略的研究。文獻[5]針對主汽壓被控對象模型參數不確定的問題,采用動態矩陣算法建立了多步預測、滾動優化和反饋校正的控制策略,提高了系統的魯棒性,但并沒有對系統的非線性作補償,因此不能滿足工程實際需要。文獻[6]通過Smith預估器對主汽壓的純滯后進行補償,利用RBF神經網絡對PID控制器參數進行整定,進一步提高了主汽壓控制系統的穩定性,但其本質上還是PID控制,對主汽壓系統大慣性的抑制能力較弱,導致波形波動較大。文獻[7]針對鍋爐主汽壓設計了一種延遲觀測器的滑模控制策略,實現了蒸汽壓力的一階及二階導數的延遲觀測,具有較好的跟蹤性能,但該研究只局限于理論分析仿真,并沒有在實際工程中開展應用。

滑模控制(SMC)采用可變結構的控制原理,是一種特殊的非線性控制方法,其滑動模態控制律為非線性函數,控制策略根據系統的結構做出相應改變,因此對于處理模型參數易變的非線性系統效果良好[8-9]。減小高頻抖振是滑模控制器設計的一個重要環節[10-11],而廣義預測控制(GPC)是一種基于多步預測、滾動優化和反饋校正的自適應控制策略[12]。

綜上,本文提出了將兩種控制方法相結合的主汽壓優化控制策略,利用GPC對SMC的增益進行實時預測,并通過在線反饋校正來降低SMC控制系統的抖振,同時對主汽壓控制器采取分步滾動優化驟,從而達到有效抑制主汽壓控制系統擾動的目的。

1 主汽壓控制系統構建

1.1 主汽壓系統動態特性分析

對燃氣發電鍋爐燃燒系統的動態特性進行分析是設計主汽壓控制系統的前提。由文獻[13],鍋爐燃燒系統的動態模型通常表示成

(1)

式中:y1、y2、y3分別是主汽壓(MPa)、爐膛負壓(Pa)和煙氣含氧量;u1、u2、u3分別是燃氣體積流量(m3/s)、送風流量(m3/s)和引風流量(m3/s)。

整個燃燒系統包含主汽壓、空氣過剩系數和爐膛負壓共3個控制回路。系統輸入變量是燃氣體積流量、冷空氣送風流量和煙氣引風流量;輸出變量分別是主汽壓、空氣過剩系數和爐膛負壓。由于燃氣量變化對主汽壓的影響最為直接,所以一般采用燃氣量作為主汽壓系統的控制量[14]。

鑒于PID控制原理簡單且工程應用廣泛[15-16],因此在鍋爐主汽壓控制系統中常使用PID控制。主汽壓控制器主要用來穩定主蒸汽壓力,燃氣供應控制器通過調節燃氣流量間接達到穩定主汽壓的目的。主汽壓控制器的輸出由燃氣控制器跟蹤。引入空燃比系數α,將α和燃氣供應控制器輸出相乘的結果作為送風量的設定值,以確保燃料充分燃燒,提高鍋爐運行效率。爐膛負壓則由煙氣引風機控制在負壓的設定值。主汽壓變化主要是由燃氣流量變化和主蒸汽流量變化引起的,在鍋爐正常穩定運行條件下,主蒸汽流量變化很小,可以認為其是穩定的。因此,主汽壓傳遞函數可以表示成一階加時延過程模型

(2)

式中:K是比例系數;τ是延遲時間;T是時間常量。

1.2 主汽壓控制方案設計

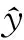
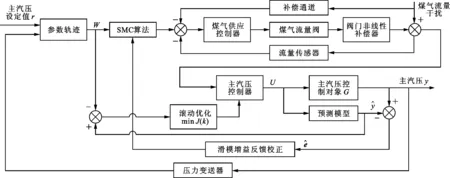
J(k)—k時刻滾動優化性能指標函數;U—控制器輸出。圖1 主汽壓PSMC整體控制方案

煤氣調節閥作為主汽壓控制系統的執行器,其流量的非線性特性是造成主汽壓系統非線性的主要原因。本文對采用的煤氣電液數字調節閥的控制信號占空比進行非線性補償,以改善調節閥流量的非線性特性,進一步提高主汽壓控制系統的穩定性。電液數字調節閥的流量特性由死區、線性區和飽和區共3個部分組成,對死區和飽和區的控制信號占空比進行補償,補償公式分別為

(3)

(4)

式中:Tc為閥門控制信號周期;t1、t2、t3、t4分別為閥芯的吸合延遲時間、吸合運動時間、釋放延遲時間、釋放運動時間(ms);D為控制器輸出的控制信號占空比;Dcom為補償后的控制信號占空比。以HSV-3101S1型電液數字閥門為例進行計算,對應的閥門控制信號周期Tc為30 ms,對不同開度下的流量特性進行分析,得出參數t1、t2、t3、t4分別為1.5、1、1.5、1 ms。因此,基于死區、線性區和飽和區的分段補償控制信號占空比為

(5)

2 滑模預測控制器設計

GPC控制的主汽壓預測模型由階躍響應數據建立,通過燃氣發電鍋爐運行現場的階躍響應實驗,可以得到主汽壓采樣值αi=α(iTp),i=1,2,…,N,其中Tp為采樣周期,N為預測范圍。根據線性系統疊加原理,k時刻對k+i時刻的主汽壓輸出預測值為

(6)

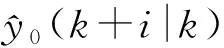
SMC控制器的設計步驟如下。

(1)滑模函數設計。根據系統主汽壓設定值r(t)和輸出測量值y(t)之間的偏差e(t)來定義滑模函數,得到

(7)

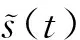
(2)控制律設計。控制律設計具體包含兩部分:①當e(t)較小時,設計連續部分來控制主汽壓系統;②當系統受干擾時,設計不連續部分,通過改變系統結構以維持主汽壓穩定。連續部分使用等效滑模控制進行設計,等效滑模控制必須滿足

(8)

將式(8)代入式(7),可得

(9)

由于e(t)=r(t)-y(t),所以式(9)可表示成

(10)

在微分域中用式(2)替換式(10),可得

(11)

因此,等效滑模控制律可表示成

(12)

由文獻[17]可知,舍棄系統設定值的微分,不影響系統的控制性能,因此式(12)變為

(13)

同樣,由文獻[17]可知,η1最佳值取為

(14)

文獻[18]已證明η2的最佳值為

(15)

因此,等效滑模控制律的離散形式表示為

(16)

(3)到達模式控制律設計。到達模式控制律設計用于改變系統結構,使位于滑模面之外的系統狀態盡快到達滑模面上。本文采用GPC獲得最佳預測增益Kp以取代到達模式控制律中的固定增益Ks,復合控制律表示為

(17)

式中:Ks與滑模運動到達滑模面的速度有關;調節β可以確保主汽壓控制動作的平穩性。由文獻[19]的時域性能方法可知,控制器的調節參數為

(18)

(19)

預測控制是基于離散系統的,因此將主汽壓被控對象式(2)進行離散化,得到

(20)

式中:d1=e-Tp/T;n1=K(1-d1);d=τ/Tp。為計算方便,時延τ取整數且為Tp的整數倍。

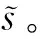
(21)

基于Kp和sp的到達模式控制律表示為

(22)

式中kGPC是增益矩陣KGPC的首行。

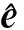
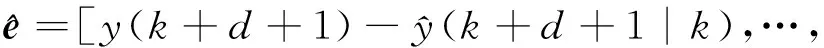
(23)

KGPC為

(24)

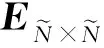
k時刻滾動優化性能指標函數為

(25)

式中:W(k+j)為主汽壓系統未來k+j時刻的設定參考值;λ為控制權重,表示對控制量變化Δu的抑制,引入λ可降低主汽壓調節過程中的劇烈波動。性能指標J通過式(22)中的Kp達到最小值,此時主汽壓預測值與設定參考值最接近。

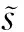
W(k+d+1)-W(k)

(26)

將式(16)和式(26)相加,可得離散滑模預測控制律的完整表達式

UPSMC(k)=Ueq(k)+Ureach(k)

(27)

PSMC控制器共含5個調節參數,其中,η1、η2、β分別由式(14)(15)(19)給出,預測范圍N和控制權重λ通常選擇常數,且N越大,系統計算時間越長,而λ越大,系統響應越慢。考慮到控制器性能,N和λ取值不宜過大。

3 仿真分析

以某發電廠42 MW火電機組150 t燃氣鍋爐作為被控對象進行仿真研究,采用最小二乘辨識法對燃氣鍋爐主汽壓模型參數進行辨識,辨識過程如圖2所示。

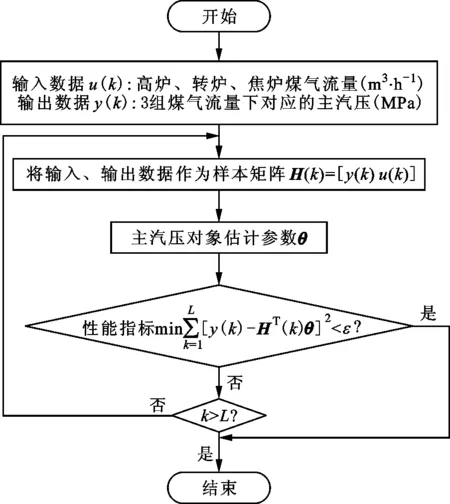
L—辨識循環次數。圖2 主汽壓模型參數辨識流程

對燃氣鍋爐運行現場的3 600組高爐、轉爐、焦爐煤氣量和在3組煤氣量下對應的主汽壓數據進行剔除異值、平滑處理等預處理,作為參數辨識的輸入數據和輸出數據。辨識循環次數L為3 600,辨識精度ε為0.00 1。當系統辨識過程達到精度要求時,得到主汽壓近似數學模型,其傳遞函數為

(28)

系統采樣周期為1 ms,主汽壓初始狀態為1。將常規PID、SMC和動態矩陣控制(DMC)共3種控制方案與PSMC控制策略進行仿真對比。PID參數根據Ziegler-Nichols整定方法選取[20],PSMC中的廣義預測參數N和λ以及DMC的參數均根據預測控制的一般參數選取規則進行選取,各控制器參數如表1所示,表中,DMC的參數H為模型長度,P為優化時域,M為控制時域,Q和R分別是誤差權矩陣和控制權矩陣,對應的初始值分別取P維單位矩陣EP×P和0矩陣。

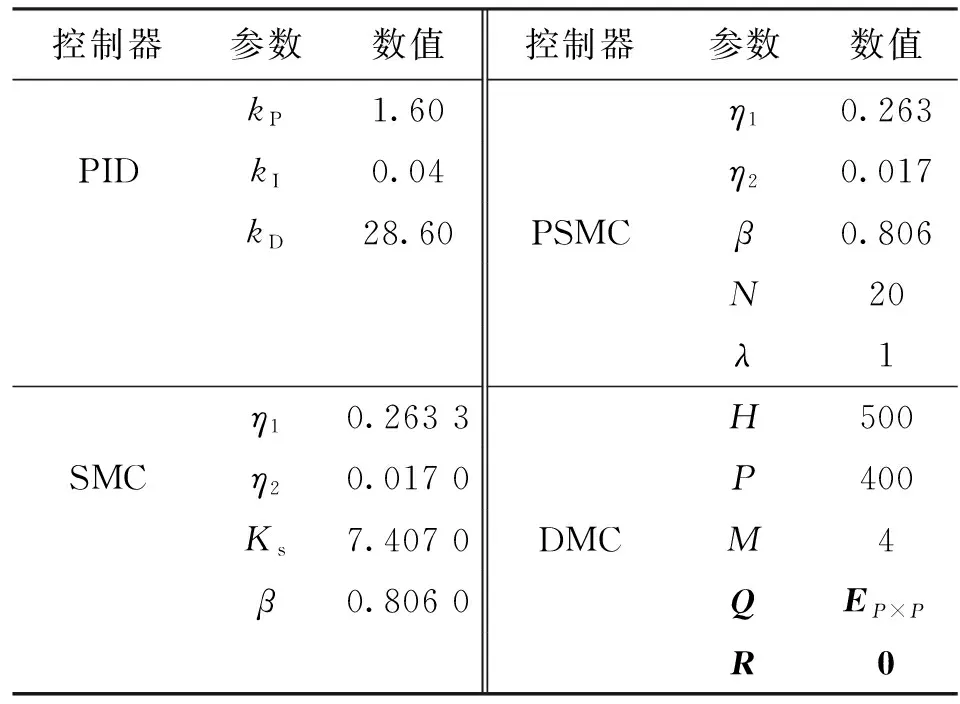
表1 燃氣鍋爐控制器參數

為驗證PSMC控制策略的跟蹤性能和抗干擾性能,向主汽壓系統施加0.2sint的干擾信號,主汽壓設定信號為r=sint。

(1)固定增益SMC控制仿真。采用式(17)的控制律,SMC控制的跟蹤曲線及跟蹤誤差如圖3所示。

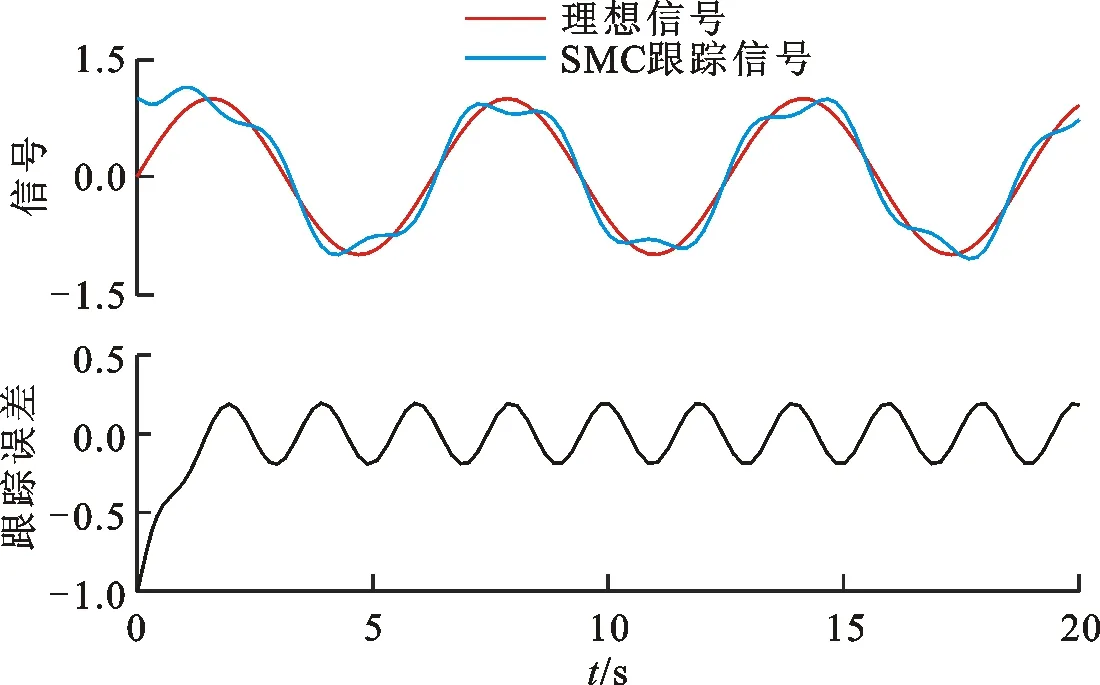
圖3 SMC控制的跟蹤曲線及跟蹤誤差

(2)預測增益PSMC控制仿真。采用式(27)的控制律,PSMC控制的跟蹤曲線及跟蹤誤差如圖4所示,SMC和PSMC控制的對應滑模函數如圖5所示。

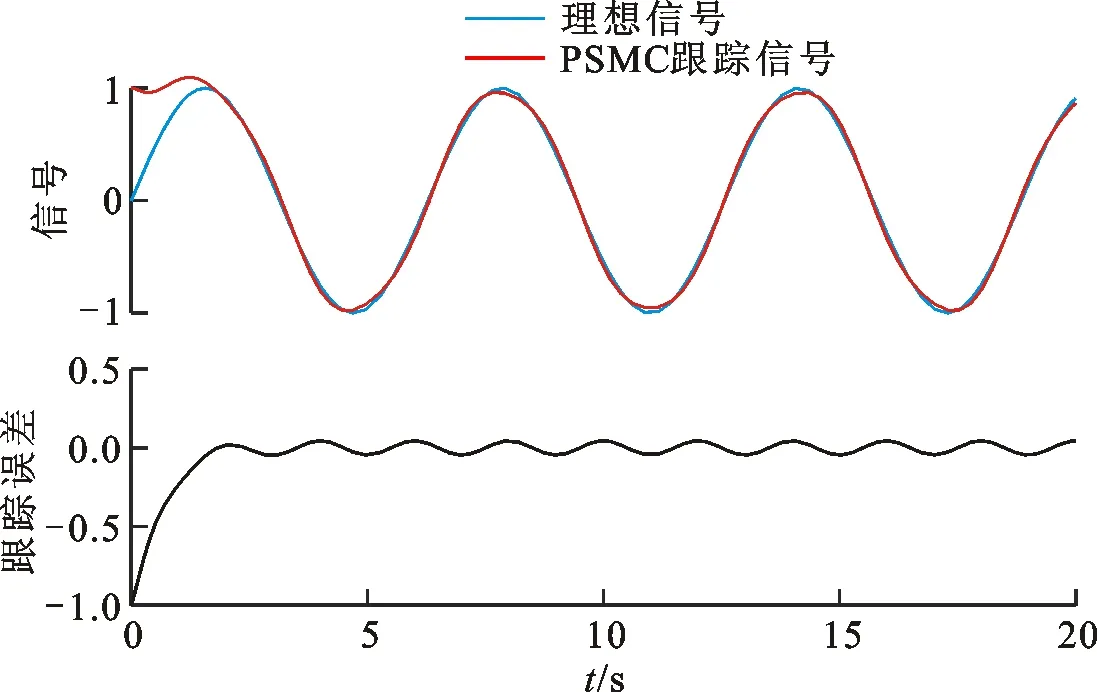
圖4 PSMC控制跟蹤曲線及跟蹤誤差

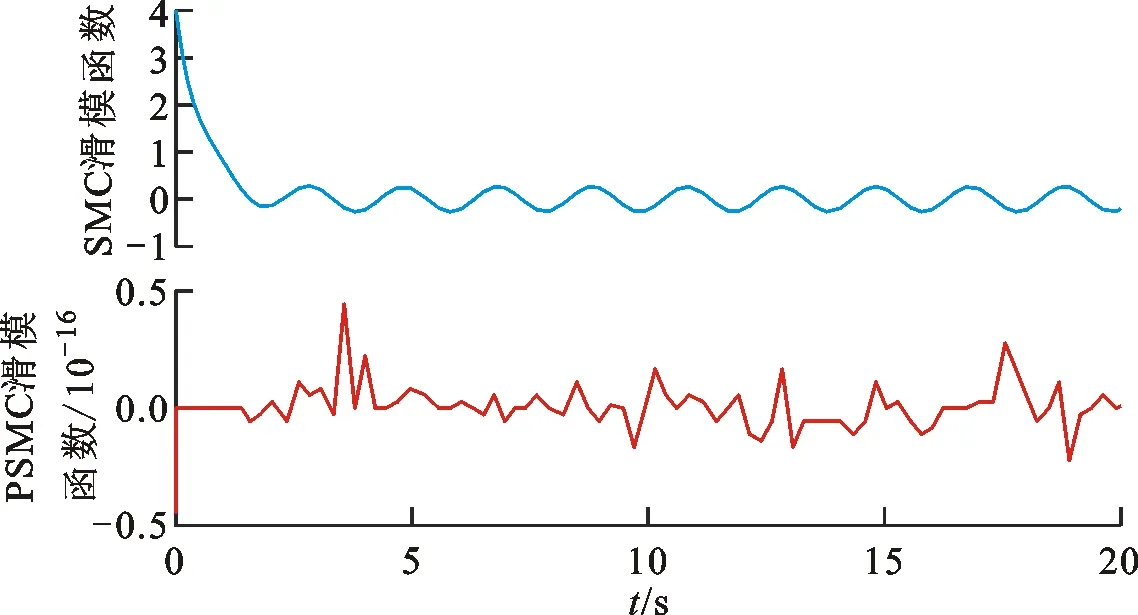
圖5 SMC和PSMC控制的滑模函數

從圖3和圖4可以看出,在相同的正弦干擾信號下,采用SMC控制的跟綜誤差在±0.25之間,而采用PSMC控制的跟綜誤差在±0.05之間,PSMC較SMC控制的跟綜性能和抗干擾性能較好。從圖5可以看出,PSMC對SMC控制的固定增益進行了預測優化,滑模函數更加平坦,幾乎無波動,系統抖振得到有效遏制。

(3)前饋和非線性補償仿真比較。在PSMC控制策略下,對煤氣擾動和煤氣調節閥分別進行前饋及非線性補償仿真對比,結果如圖6所示。

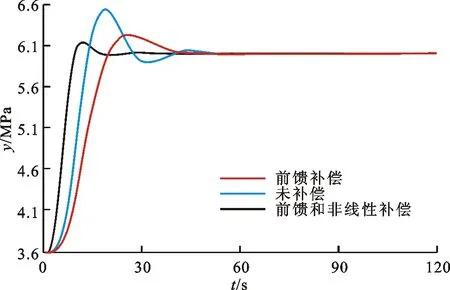
圖6 PSMC下煤氣擾動及調節閥的前饋和非線性補償結果對比

從圖6可以看出:未對煤氣擾動和煤氣調節閥進行補償時的系統超調量為9.17%,主汽壓調節過程中波動較大;對煤氣擾動進行前饋補償時的超調量為5.02%;對煤氣擾動及煤氣調節閥分別進行前饋和非線性補償時的超調量分別為2.81%,主汽壓波動得到有效抑制,系統穩定性顯著提高。

(4)模型適配與失配仿真比較。在式(28)主汽壓精確模型仿真的基礎上,對K、τ和T均增大10%進行仿真,以此模擬模型失配情況下PSMC控制策略的魯棒性,結果如圖7、圖8所示。從圖7可以看出,在主汽壓模型參數精確時:采用PSMC控制的超調量為5.1%,調節時間為39.3 s;采用SMC控制的超調量為15.3%,調節時間為40.2 s;采用DMC控制的超調量為18.2%,調節時間為43.4 s;采用常規PID控制時的超調量為21.5%,調節時間為58.4 s。從圖8可以看出,在主汽壓模型參數失配時:采用PSMC控制的超調量為5.8%,調節時間為40.4 s;采用SMC控制的超調量為18.9%,調節時間為42.1 s;采用DMC控制的超調量為17.5%,調節時間為40.8 s;采用常規PID控制的超調量為27.8%,調節時間為63.6 s。分析表明,PSMC控制策略在主汽壓模型失配的工況下具有更強的魯棒性。

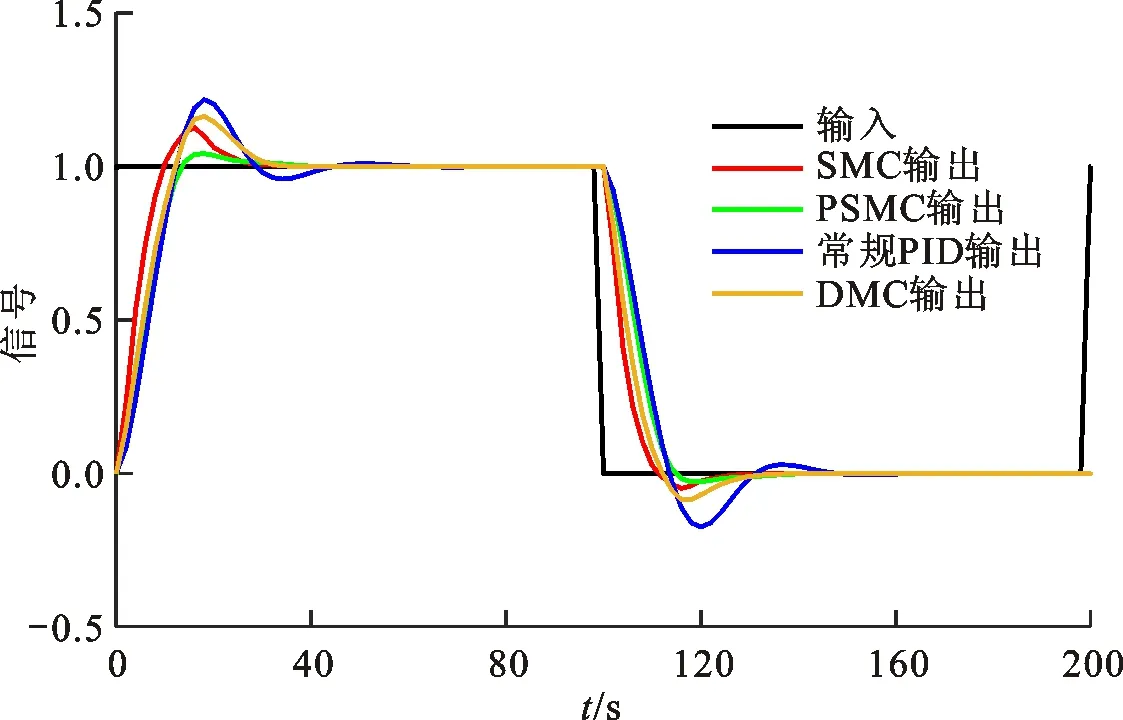
圖7 模型參數準確時4種控制策略的仿真

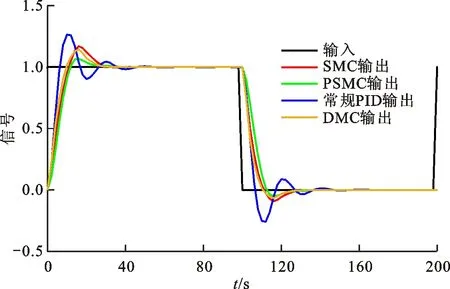
圖8 模型參數不準確時4種控制策略的仿真

4 工程應用

為驗證PSMC控制策略的有效性,以某發電廠42 MW火電機組150 t燃氣發電鍋爐主汽壓為控制對象進行工程應用。在保持原有集散控制系統(DCS)配置不變的基礎上,增加一套由工業控制計算機和優化控制器組成的鍋爐主汽壓優化控制系統。整個優化控制系統的拓撲結構如圖9所示。本文設計的PSMC控制策略程序在CoDesys軟件中編寫,下載到PLC中運行。數據采集和傳輸通過Kepware進行,Kepware軟件將DCS系統中的數據通過OPC服務器與CoDesys服務器中的數據進行交換,實現數據的共享。利用力控軟件建立監控畫面,讀取CoDesys中的數據到組態畫面中,并對數據的歷史趨勢進行保存,實現報表統計、考核、參數設置、手自動切換和語言報警等功能。

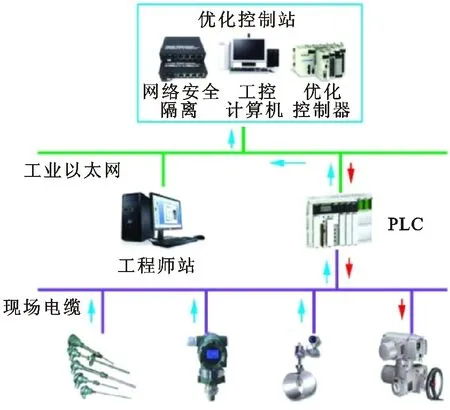
圖9 主汽壓優化控制系統

圖10～12是在燃氣鍋爐額定負荷下連續3天分別采用常規PID控制、SMC控制和PSMC控制的主汽壓實時曲線,主汽壓設定值為6 MPa,每次監測時間為8小時。從圖10～12可知:采用常規PID控制的主汽壓在5.7～6.2 MPa之間波動,波動范圍較大,這是因為常規PID控制系統存在慣性,無法及時抑制因煤氣擾動帶來的主汽壓變化;采用SMC控制和PSMC控制的主汽壓分別在5.85～6.1 MPa以及5.95～6.05 MPa之間波動;相較SMC控制,PSMC控制的系統抖振降低了60%,主汽壓曲線沒有出現明顯的波峰和波谷,整體走勢平穩,系統穩定性和抗干擾能力明顯提高。

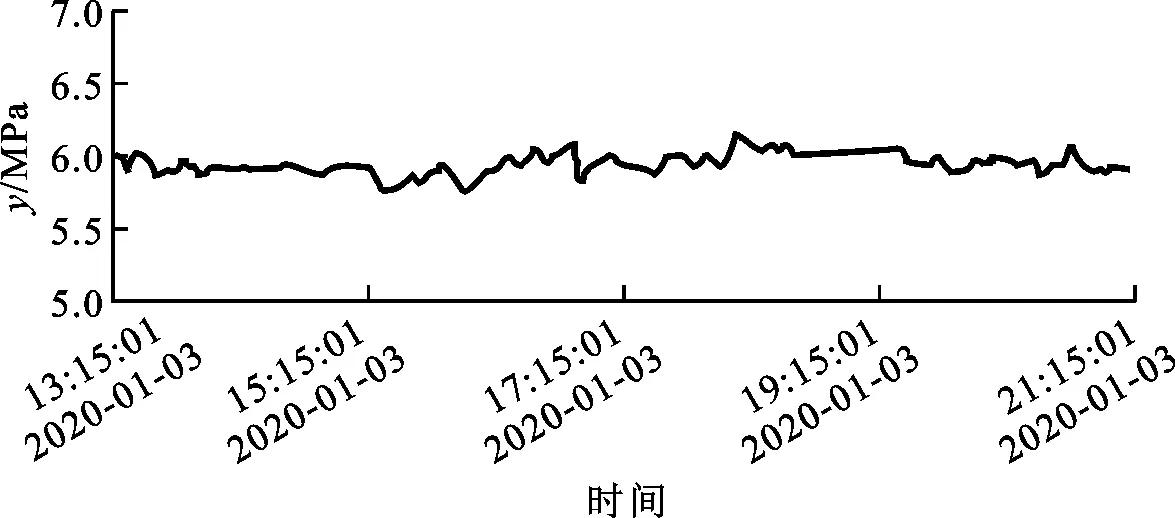
圖10 PID控制的主汽壓實時曲線

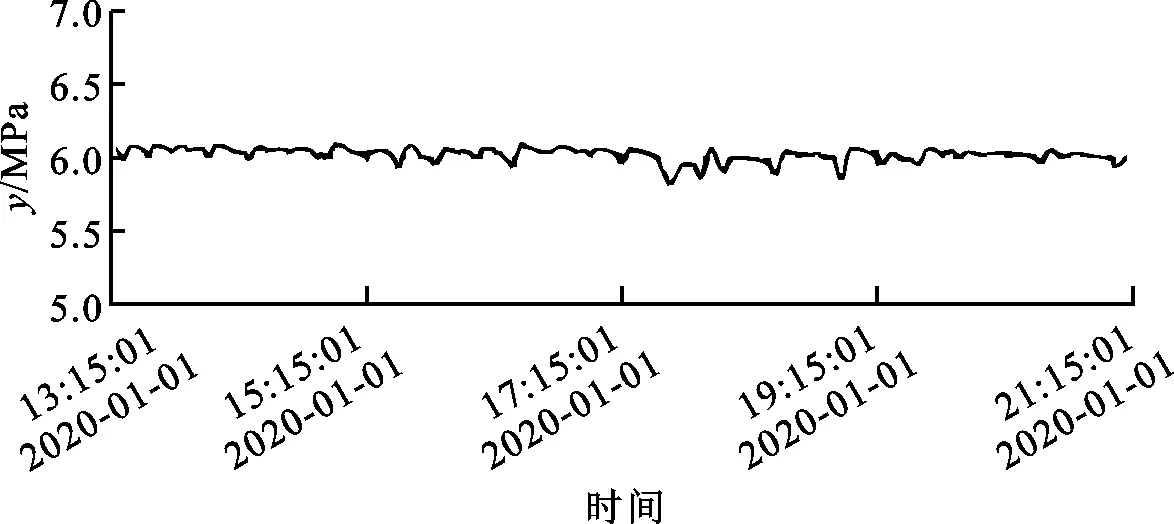
圖11 SMC控制的主汽壓實時曲線

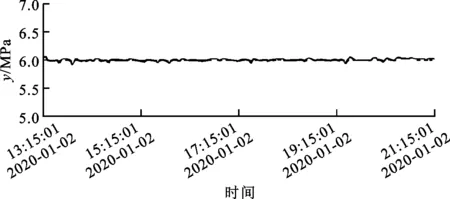
圖12 PSMC控制的主汽壓實時曲線

5 結 論

燃氣發電鍋爐主汽壓控制系統具有非線性、純滯后的特點,且機組運行時受現場擾動大,被控對象模型參數易變。鑒于常規控制方法無法達到理想的控制效果,本文提出了一種PSMC的主汽壓優化控制策略,采用GPC預測SMC的增益并在線校正更新,在此基礎上對主汽壓控制器進行滾動優化,進一步提高控制器的控制性能。仿真結果表明,本文PSMC控制策略跟蹤性能良好、抗干擾能力強,在主汽壓超調量和調節時間等性能指標方面均優于常規PID、SMC和DMC控制的,具有更強的魯棒性。工程應用表明,采用本文PSMC控制策略后,系統抖振比單一SMC控制的降低60%,主汽壓的控制偏差在±0.05 MPa以內,有效提高了發電機組運行的安全性和主汽壓控制系統的穩定性。

本文提出的PSMC控制策略對于其他燃煤或燃油發電鍋爐的主汽壓控制應具有一定的借鑒意義。