思維導(dǎo)圖在高等數(shù)學(xué)教學(xué)中的應(yīng)用及方法探究
邵 莉,周 娟
(信陽(yáng)職業(yè)技術(shù)學(xué)院,河南 信陽(yáng) 464000)
0 引言
高等數(shù)學(xué)是由微積分學(xué)、代數(shù)學(xué)、幾何學(xué)以及它們的交叉內(nèi)容所組成的一門基礎(chǔ)學(xué)科。它具有高度的抽象性、嚴(yán)密的邏輯性和廣泛的應(yīng)用性等特點(diǎn),在基本概念表述、判斷和推理中都要用到邏輯的規(guī)則,遵循思維的規(guī)律。因此,可以說學(xué)習(xí)高等數(shù)學(xué)的過程也是思維訓(xùn)練的過程。采用傳統(tǒng)的教學(xué)理念和教學(xué)手段,展開高等數(shù)學(xué)教學(xué)活動(dòng),學(xué)生學(xué)習(xí)的整體積極性并不高,對(duì)于高等數(shù)學(xué)基礎(chǔ)知識(shí)掌握也不深刻,亟待教師進(jìn)行教學(xué)實(shí)踐創(chuàng)新探索。思維導(dǎo)圖作為一種教學(xué)工具,以建構(gòu)教育理念為基礎(chǔ),衍生的一種新型教學(xué)理念[1],在高等數(shù)學(xué)人才培養(yǎng)中的積極作用,已然成為其他學(xué)科教學(xué)改革的參考對(duì)象,因此,進(jìn)一步構(gòu)建基于思維導(dǎo)圖的高等數(shù)學(xué)教學(xué)體系,是教師需要完成的重要教學(xué)任務(wù)。
1 高等數(shù)學(xué)教學(xué)目標(biāo)
高等數(shù)學(xué)是高等院校理工類專業(yè)的一門必修課,它能夠?yàn)閷W(xué)生學(xué)習(xí)專業(yè)課提供服務(wù),還可以為學(xué)生繼續(xù)深造創(chuàng)造條件。傳統(tǒng)的教學(xué)主要是理論授課為主,對(duì)于知識(shí)的應(yīng)用方面講解不夠深入。在新時(shí)代背景下,學(xué)生不僅僅需要學(xué)習(xí)基礎(chǔ)知識(shí),更需要掌握相關(guān)知識(shí)與專業(yè)課有效結(jié)合的途徑,提升自身專業(yè)知識(shí)和技能。
1.1 培育創(chuàng)新與自主能力
高校教學(xué)改革與創(chuàng)新的背景下,要求將創(chuàng)新精神和應(yīng)用能力的培養(yǎng),提高到素質(zhì)教育的重要位置,改革傳統(tǒng)教學(xué)理念,樹立以學(xué)生為主體,以學(xué)生綜合能力培育為目標(biāo)的教學(xué)理念。讓學(xué)生能夠在高等數(shù)學(xué)學(xué)科學(xué)習(xí)中,掌握知識(shí)體系結(jié)構(gòu)內(nèi)容,同時(shí)培養(yǎng)學(xué)生的自主學(xué)習(xí)和創(chuàng)新能力。在高等數(shù)學(xué)教學(xué)過程中,不僅要不斷適應(yīng)教學(xué)改革的步伐,還要能掌握“用文字、圖表以及數(shù)學(xué)方式等多種表達(dá)形式準(zhǔn)確性地描述高等數(shù)學(xué)方面的內(nèi)容”的能力,解決一些復(fù)雜的高等數(shù)學(xué)問題,將抽象問題直觀化,幫助學(xué)生對(duì)高等數(shù)學(xué)知識(shí)的理解和掌握更加靈活、全面,以提升學(xué)生的學(xué)習(xí)效率。所以,在高等數(shù)學(xué)教學(xué)中,教師一定要注重培養(yǎng)學(xué)生的創(chuàng)新和自主能力,能真正解決問題,學(xué)以致用,這也是教學(xué)的最高戰(zhàn)略目標(biāo)和任務(wù)。
1.2 邏輯思維的培育
從根本上來說,數(shù)學(xué)知識(shí)的學(xué)習(xí)不僅僅是學(xué)習(xí)工具、方法,更是邏輯思維的培育過程。邏輯思維是人的理性認(rèn)知部分,是人利用現(xiàn)有認(rèn)知進(jìn)行判斷、推理等思維活動(dòng)從而認(rèn)識(shí)事物本質(zhì)及規(guī)律的過程。邏輯思維的思維方式在數(shù)學(xué)這門學(xué)科中表現(xiàn)的異常突出,也是人類認(rèn)識(shí)世界、改造世界最重要的思維方式之一。
1.3 知識(shí)融合的基礎(chǔ)
現(xiàn)今高等數(shù)學(xué)教育僅僅只針對(duì)數(shù)學(xué)知識(shí)的學(xué)習(xí),但從社會(huì)和知識(shí)體系的發(fā)展現(xiàn)狀和未來前景來看,高等數(shù)學(xué)必須也必然成為一種交叉學(xué)科的黏合劑,其作為工具、方法,將不同的學(xué)科、知識(shí)融合起來,以解決復(fù)雜且不斷變化的現(xiàn)實(shí)問題。
2 在高等數(shù)學(xué)教學(xué)中應(yīng)用思維導(dǎo)圖的意義
思維導(dǎo)圖(MindMap)又叫心智導(dǎo)圖、思維地圖、樹枝圖、靈感出發(fā)圖等,是從一個(gè)中心點(diǎn)開始的。每個(gè)詞或者圖像自身都成為子中心,整個(gè)合起來以一種無(wú)限的分支鏈的形式從中心向四周放射,或者歸于一個(gè)共同的中心[2]。
構(gòu)建高等數(shù)學(xué)學(xué)科的思維導(dǎo)圖,需要以高等數(shù)學(xué)理論知識(shí)為基礎(chǔ),掌握各個(gè)定理、概念之間的深層次關(guān)系,基于高等數(shù)學(xué)教學(xué)大綱內(nèi)容,明確每一個(gè)思維導(dǎo)圖節(jié)點(diǎn)所要達(dá)到的教學(xué)目標(biāo),完成對(duì)相關(guān)知識(shí)點(diǎn)子脈絡(luò)的排序,構(gòu)建更加龐大的具有層次關(guān)系的思維導(dǎo)圖。
2.1 思維導(dǎo)圖有利于改善碎片化知識(shí)點(diǎn)的教學(xué)效果
高等數(shù)學(xué)學(xué)科本身具有繁雜的知識(shí)體系,其知識(shí)內(nèi)容在教學(xué)中難免出現(xiàn)碎片化現(xiàn)象,某一知識(shí)點(diǎn)既同上個(gè)章節(jié)內(nèi)容有關(guān)聯(lián),卻也導(dǎo)向下一章節(jié)內(nèi)容。因此,在學(xué)習(xí)過程中,學(xué)生往往會(huì)忽視知識(shí)點(diǎn)之間的關(guān)聯(lián)性,無(wú)法構(gòu)建高等數(shù)學(xué)整體知識(shí)體系。而思維導(dǎo)圖有層次性,能夠?qū)⒛骋粋€(gè)章節(jié)知識(shí)點(diǎn)構(gòu)建成網(wǎng)格結(jié)構(gòu)圖,尋找每一個(gè)章節(jié)知識(shí)點(diǎn)之間的深層關(guān)聯(lián)性,從而挖掘到碎片化知識(shí)點(diǎn)的承上啟下作用。同時(shí),通過思維導(dǎo)圖,能夠讓每一個(gè)知識(shí)點(diǎn)都分到一個(gè)圖示節(jié)點(diǎn),學(xué)生能夠?qū)Ω叩葦?shù)學(xué)教學(xué)知識(shí)有清晰的認(rèn)識(shí),在遇到相關(guān)問題的時(shí)候,通過回憶圖示節(jié)點(diǎn)上下左右的關(guān)系節(jié)點(diǎn),對(duì)問題進(jìn)行深度探索,尋求解決方法。
2.2 知識(shí)可視化促進(jìn)高等數(shù)學(xué)知識(shí)的應(yīng)用
知識(shí)可視化是將抽象的知識(shí)具象化的過程,知識(shí)以可視的形式出現(xiàn),方便知識(shí)的記憶、理解以及運(yùn)用[3]。相對(duì)于抽象化的過程,具象化的稱號(hào)、圖形更容易被快速識(shí)別、運(yùn)用,同時(shí)也將抽象的思維外顯,有利于了解他人的思維方式,產(chǎn)生思維碰撞。
高等數(shù)學(xué)教學(xué)是抽象的,將抽象的知識(shí)進(jìn)行綜合性應(yīng)用是教學(xué)中的重難點(diǎn)。對(duì)于高等數(shù)學(xué)教學(xué)實(shí)踐活動(dòng)而言,往往會(huì)出現(xiàn)學(xué)生清楚掌握每一章節(jié)的知識(shí)內(nèi)容,但是,遇到綜合性應(yīng)用問題時(shí),無(wú)法利用知識(shí)去解決實(shí)際問題。而思維導(dǎo)圖有清晰的圖形結(jié)構(gòu),將高等數(shù)學(xué)知識(shí)以簡(jiǎn)單的圖示節(jié)點(diǎn)的形式呈現(xiàn)出來。如,一元函數(shù)連續(xù)性知識(shí)點(diǎn)教學(xué),其橫向可以展開二元函數(shù)知識(shí)教學(xué),縱向可展開極限等知識(shí)教學(xué)。在實(shí)踐中,并不是單純的要求學(xué)生展開一元函數(shù)的連續(xù)性求證,而是聯(lián)系極限知識(shí)進(jìn)行拓展應(yīng)用。若借助思維導(dǎo)圖,學(xué)生在分析問題、知道問題所要考核的內(nèi)容是關(guān)于一元函數(shù)時(shí),可以在腦海中形成一元函數(shù)的相關(guān)思維導(dǎo)圖,繼而從橫向、縱向兩個(gè)方面來解答問題[4]。思維導(dǎo)圖在很大程度上激發(fā)了學(xué)生問題探索的能力,對(duì)于培育學(xué)生的創(chuàng)新性思維能力也有著重要的影響。
3 思維導(dǎo)圖在高等數(shù)學(xué)教學(xué)中的應(yīng)用及方法
3.1 發(fā)揮學(xué)生主體性,構(gòu)建個(gè)性化思維導(dǎo)圖
思維導(dǎo)圖的構(gòu)建并不存在惟一標(biāo)準(zhǔn)答案,其主要在于學(xué)生對(duì)高等數(shù)學(xué)知識(shí)的理解,自我探索能力以及對(duì)思維導(dǎo)圖的構(gòu)建方法的掌握。當(dāng)前,在高等數(shù)學(xué)教學(xué)活動(dòng)中,要想發(fā)揮思維導(dǎo)圖的積極作用,必須樹立以學(xué)生為主體的教學(xué)理念[5],學(xué)習(xí)的過程,自主學(xué)習(xí)的效果一般情況下遠(yuǎn)高于被動(dòng)的學(xué)習(xí)過程,教授思維導(dǎo)圖的繪制原則、理念給學(xué)生的方式,更應(yīng)該采用能發(fā)揮學(xué)生主體性和自覺性的方式。現(xiàn)在的學(xué)生對(duì)于手機(jī)和電子產(chǎn)品的依賴程度很高,很多情況下這些電子產(chǎn)品阻礙了學(xué)生的學(xué)習(xí),但在這里我們完全可以利用這些電子設(shè)備讓學(xué)生學(xué)會(huì)信息檢索,并進(jìn)一步嘗試解決問題,讓學(xué)生根據(jù)自己查找到的相關(guān)信息去理解思維導(dǎo)圖,并進(jìn)行繪制。
與此同時(shí),可以適當(dāng)改變教學(xué)活動(dòng)的進(jìn)行方式,教與學(xué)并不一定是老師講學(xué)生聽,也可以是以問題為導(dǎo)向,學(xué)生講老師聽。學(xué)生自由組合,分工合作,構(gòu)建自己所在的分組關(guān)于某個(gè)知識(shí)點(diǎn)的思維導(dǎo)圖,并對(duì)老師以及其他同學(xué)進(jìn)行講解,由老師進(jìn)行點(diǎn)評(píng)和修正。甚至可以將這種答辯式的教學(xué)模式改革代入高等數(shù)學(xué)的考核方式改革,從根本上改變高等數(shù)學(xué)的教學(xué)現(xiàn)狀。
對(duì)于學(xué)生來說,這種高度互動(dòng)的方式有利用對(duì)自己構(gòu)建的高等數(shù)學(xué)思維導(dǎo)圖,展開積極討論并對(duì)思維導(dǎo)圖進(jìn)行優(yōu)化升級(jí),在不斷拓展思維導(dǎo)圖的同時(shí),完成對(duì)高等數(shù)學(xué)知識(shí)的深度探索。發(fā)揮學(xué)生的自主探索能力,在自主探索下創(chuàng)建的思維導(dǎo)圖,更有利于學(xué)生學(xué)習(xí)知識(shí)、掌握知識(shí),同時(shí),培養(yǎng)了學(xué)生的邏輯推理能力、綜合應(yīng)用能力和創(chuàng)新精神。從教師的角度看待,這種高度的互動(dòng)教學(xué)方式首先可以改善教學(xué)環(huán)境,活躍課堂氣氛,將學(xué)生和老師從枯燥的課堂內(nèi)容中解放出來;其次,高度的互動(dòng)中學(xué)生表達(dá)的較多,有利用教師更深入的了解學(xué)生的發(fā)展?fàn)顩r,從而有針對(duì)性的幫助處于不同學(xué)習(xí)階段的學(xué)生,畢竟學(xué)生的發(fā)展和進(jìn)步并不僅僅是知識(shí)的增長(zhǎng)。
3.2 借助信息技術(shù),構(gòu)建多元化的思維導(dǎo)圖
在信息時(shí)代,計(jì)算機(jī)技術(shù)已經(jīng)掀起教育活動(dòng)的轉(zhuǎn)型升級(jí),對(duì)于高等數(shù)學(xué)教學(xué)活動(dòng)而言,計(jì)算機(jī)技術(shù)同樣發(fā)揮著重要作用。一方面,計(jì)算機(jī)技術(shù)能夠?yàn)楦叩葦?shù)學(xué)教學(xué)帶來更多的教學(xué)資源。如,可以通過計(jì)算機(jī)技術(shù),構(gòu)建起在線經(jīng)典高等數(shù)學(xué)教學(xué)案例,為學(xué)生們提供更多高等數(shù)學(xué)教學(xué)資源;另一方面,信息技術(shù)支持下,教學(xué)形式多元化發(fā)展,特別是思維導(dǎo)圖的引入,有利于學(xué)生的興趣激發(fā),能夠有效地吸引學(xué)生的學(xué)習(xí)注意力,激發(fā)學(xué)生對(duì)高等數(shù)學(xué)知識(shí)學(xué)習(xí)的積極參與性。目前,在線思維導(dǎo)圖工具有百度腦圖、ProcessOn、Coggle 和幕布等;思維導(dǎo)圖軟件有Freemind、XMind、MindMaster、Word 等。教師可以借助上述繪圖工具或軟件,利用形式多樣的樹狀圖、網(wǎng)絡(luò)圖的繪制,導(dǎo)入各種動(dòng)態(tài)形式,完成多樣化的思維導(dǎo)圖繪制。如,我們知道微積分學(xué)是高等數(shù)學(xué)的主要部分,函數(shù)是微積分學(xué)研究的主要對(duì)象,而極限則是微積分學(xué)的基礎(chǔ),也是最主要的推理方法。由此,聯(lián)想到函數(shù)連續(xù)、導(dǎo)數(shù)及定積分的表達(dá)式都用到極限,故以極限為中心詞,可推導(dǎo)出函數(shù)連續(xù)性、導(dǎo)數(shù)和定積分等重要內(nèi)容。其中函數(shù)求導(dǎo)數(shù)和求不定積分是互逆的過程,可以說不定積分與導(dǎo)數(shù)相關(guān)。按照上述思路制作的思維導(dǎo)圖如圖1所示。
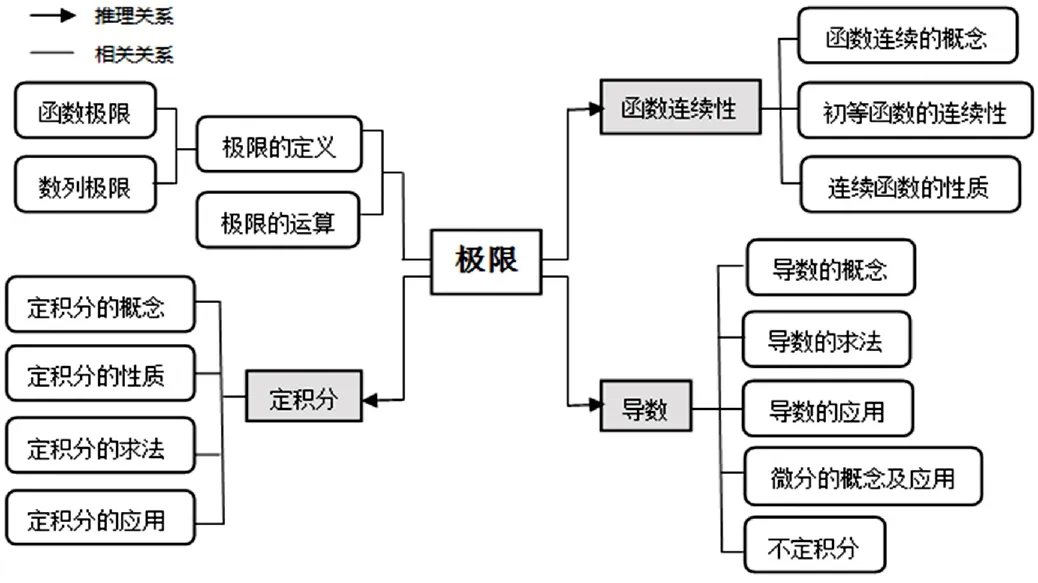
圖1 關(guān)于極限的思維導(dǎo)圖
圖1中很多知識(shí)點(diǎn)還可以繪制子圖,這里不再舉例。通過圖1思維導(dǎo)圖和子思維導(dǎo)圖的繪制,基本讓學(xué)生掌握了高等數(shù)學(xué)中一元函數(shù)微積分學(xué)的內(nèi)容。這種教學(xué)方式無(wú)論是在新知識(shí)點(diǎn)的介紹還是在高等數(shù)學(xué)的知識(shí)點(diǎn)復(fù)習(xí)總結(jié)中的應(yīng)用,都能夠營(yíng)造良好的課堂學(xué)習(xí)氛圍,激發(fā)學(xué)生對(duì)高等數(shù)學(xué)知識(shí)網(wǎng)絡(luò)結(jié)構(gòu)認(rèn)知和探索的興趣。
3.3 教學(xué)相長(zhǎng),持續(xù)改進(jìn)思維導(dǎo)圖
因?yàn)樗季S導(dǎo)圖的個(gè)性化特點(diǎn),所以不同學(xué)生和小組之間的思維導(dǎo)圖會(huì)有很大不同。不同思維、方式的碰撞會(huì)產(chǎn)生出新的火花,點(diǎn)燃學(xué)生,以思維導(dǎo)圖驅(qū)動(dòng)學(xué)生和老師,改變傳統(tǒng)的高等數(shù)學(xué)課堂,強(qiáng)化高等數(shù)學(xué)課堂上學(xué)生與老師、學(xué)生與學(xué)生之間的溝通,甚至于改變高等數(shù)學(xué)課堂上學(xué)生與老師的傳統(tǒng)地位,這對(duì)于學(xué)生的課堂學(xué)習(xí)是有益的,一方面提高了學(xué)生的學(xué)習(xí)參與度,激發(fā)了學(xué)習(xí)興趣;另一方面也增加了師生以及學(xué)生之間的溝通,對(duì)形成良好的課堂氣氛大有裨益。這種教學(xué)風(fēng)格的轉(zhuǎn)變,教師和學(xué)生地位與作用的轉(zhuǎn)型可以從根本上解決現(xiàn)今高等數(shù)學(xué)教育的一些問題,從而改善教學(xué)質(zhì)量。
另外一方面,為了學(xué)生能夠長(zhǎng)時(shí)間保持對(duì)思維導(dǎo)圖模式引導(dǎo)下高等數(shù)學(xué)學(xué)習(xí)的興趣,可以在高等數(shù)學(xué)的課堂中圍繞思維導(dǎo)圖進(jìn)行一些小實(shí)驗(yàn),根據(jù)學(xué)生的自主選擇成立對(duì)照組,實(shí)際觀察使用思維導(dǎo)圖模式學(xué)習(xí)的和不用思維導(dǎo)圖學(xué)習(xí)的不同對(duì)照組對(duì)于某個(gè)固定知識(shí)點(diǎn)的記憶和理解程度,以此推動(dòng)思維導(dǎo)圖模式在課堂上的運(yùn)用。也可以采用問卷調(diào)查或訪談的形式,一方面更為了解學(xué)生對(duì)于運(yùn)用思維導(dǎo)圖模式學(xué)習(xí)高等數(shù)學(xué)的具體情況,另一方面也加強(qiáng)了師生溝通,學(xué)生對(duì)于老師個(gè)人的認(rèn)可也是學(xué)生學(xué)習(xí)是否成功的一個(gè)重要影響因素。
4 結(jié)束語(yǔ)
在高等數(shù)學(xué)課堂教學(xué)中,運(yùn)用思維導(dǎo)圖的邏輯性,展開高等數(shù)學(xué)復(fù)雜且碎片化知識(shí)點(diǎn)的補(bǔ)充教學(xué),彌補(bǔ)教學(xué)過程中存在著的知識(shí)內(nèi)容創(chuàng)新拓展不足的問題;更重要的是思維導(dǎo)圖能夠?qū)崿F(xiàn)點(diǎn)、線、面逐層知識(shí)體系梳理,契合高等數(shù)學(xué)教學(xué)的邏輯性,大大降低了高等數(shù)學(xué)教學(xué)的難度,提升了教學(xué)質(zhì)量。另一方面,于教學(xué)過程引入思維導(dǎo)圖,引導(dǎo)學(xué)生成為課堂活動(dòng)的主體,按照自己的思維習(xí)慣和認(rèn)知習(xí)慣,構(gòu)建思維導(dǎo)圖并充分利用思維導(dǎo)圖個(gè)性化的特點(diǎn)將實(shí)踐活動(dòng)帶入到高等數(shù)學(xué)的課堂教學(xué)過程中來,產(chǎn)生思維碰撞,不斷的對(duì)現(xiàn)有的思維導(dǎo)圖進(jìn)行補(bǔ)充和改善,以保持高等數(shù)學(xué)教與學(xué)的活力,教學(xué)相長(zhǎng),實(shí)現(xiàn)高等數(shù)學(xué)教學(xué)的目標(biāo)。
- 數(shù)字通信世界的其它文章
- 基于項(xiàng)目管理體系的《單片機(jī)綜合實(shí)驗(yàn)》實(shí)踐教學(xué)方法探討
- 應(yīng)用型本科院校網(wǎng)絡(luò)協(xié)議分析課程實(shí)驗(yàn)教學(xué)改革研究
——以福州理工學(xué)院為例 - 基于數(shù)字化模擬的巖屑真實(shí)孔隙結(jié)構(gòu)細(xì)觀模型研究
- 電子信息化管理的重要作用探究
- 開關(guān)柜五防智能觸發(fā)模擬裝置功能設(shè)計(jì)和應(yīng)用
- 巧用綜合實(shí)踐活動(dòng)培養(yǎng)高中學(xué)生信息社會(huì)責(zé)任

