RAT矩函數在模態振形數據去噪中的應用

張浩，臧朝平

(南京航空航天大學 能源與動力學院，江蘇 南京 210016)

0 引言

矩函數數據去噪是最常用的形狀特征提取方法，最初矩函數主要應用在圖像識別領域。隨著研究的深入，在結構動力學領域矩函數也得到了廣泛的應用。圖像處理中最常用的矩函數為TEAGUE M R[1]提出的Zernike矩和Legengre矩兩個具有正交性的二維矩函數，可以解決幾何矩造成信息冗余的問題。但由于上述矩函數為連續函數，因此在計算時使用離散求和的方式，這樣不可避免地帶來很大的計算誤差。隨后MUKUNDAN R[2]提出了一個離散的矩函數，即Tchebichef矩函數。Tchebichef矩要優于Zernike矩與Legendre矩。因為Tchebichef矩是離散的正交矩，不僅能夠避免數據的冗余，還能消除連續積分離散化帶來的誤差。

基于矩函數能夠壓縮振型數據并反映結構的振動信息，王耀明[3]最早將Tchebichef矩函數引用在動力學模型確認中，并完成了對二維矩形、圓形結構的振型描述。但是二維矩函數在處理三維結構時只能使用投影等降維的方式，這樣不僅操作復雜，還會造成幾何信息的缺失。為了解決這個問題，曾亞未等[4]構建了三維的徑軸向Tchebichef矩函數(RAT矩)。但是由于RAT矩函數是定義在柱坐標下的矩函數，其只能夠描述三維圓柱結構的模態振型。

在工程中大多數航空發動機部件為變截面的曲面結構,馬健等[5]采用徑向坐標r的多項式去擬合軸向坐標z的方法，從而實現描述簡單的三維曲面機匣的模態振型，但該方法不具有通用性。本文作者采用積分的思想，將曲面機匣當作由若干圓柱機匣積累而成，并將振型數據插值到一個圈數×點數×層數的像素空間內。這樣就可以使用RAT矩函數直接描述三維曲面結構的模態振型[6]。

在工程實際中，如何保證測試數據的準確性一直都是需要研究的問題。在測試過程中會有很多因素影響測試結果的準確性，最常見的是試驗過程中噪聲的影響。若測試過程中存在很大的噪聲，會導致試驗數據準確性降低。基于RAT矩函數對曲面結構的振型描述能力，進一步研究了RAT矩函數在去噪中的應用。采用正態分布的隨機噪聲模擬實際噪聲影響，分析了不同噪聲強度下RAT矩函數的去噪能力，對將矩函數應用到工程試驗的去噪過程有重要意義。

1 RAT矩函數的模態振型描述方法

1.1 矩變換

在描述三維結構的模態振型時，將每個節點的位移看作每個像素點的灰度值，將振型數據表示為I(x,y,z)，每一個點(x,y,z)對應一個位移值I(x,y,z)。從而利用三維矩函數能夠實現對振型數據的矩變換，矩變換可表示為

?=Γ[I(x,y,z)]

(1)

式中：I(x,y,z)代表模態振型函數；Γ[*]表示對振型數據進行矩變換的過程，該過程可具體表示為

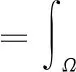
(2)

其中：?(x,y,z)表示三維矩函數，如本文使用的Radial Axial Tchebichef矩函數；Ω為矩函數自變量的取值范圍。

1.2 RAT矩函數的振型描述

RAT矩函數的表達式見如下：

(3)

其中：p=0，1，…，(N/2-1) 表示徑向的階數；q=0,1,…，m-1 表示重數；l代表的是軸向的階數,l=0,1,…,(N/2-1)；r、k、z分別是徑向坐標、周向坐標和軸向坐標；tl,h(z)和tp,m(r)分別表示軸向與徑向的Tchebichef多項式，表達如下：

(4)

(5)

對結構的振型圖像進行矩變換，從而提取出特征矩集，該過程能夠實現對龐大振型數據的壓縮處理，特征矩集的表達式見式(6)。

(6)

1.3 基于特征矩集的振型重構

通過從振型數據中提取出的特征矩集能夠重構振型圖像，重構公式如下：

(7)

引入一個總體相似度系數(GSC)的概念去評價重構振型與參考振型的相似程度，GSC的表達如下：

(8)

式中：Ω代表振型數據的定義域范圍；I′和I分別為重構的振型與原始的振型，另外：

(9)

GSC的定義如下：

(10)

GSC(i)代表RAT矩的階次為i時的每一階模態重構振型與原始振型的總體相似度系數；Smean,i與Svar,i分別為為每一階模態的重構振型圖像與原始振型圖像相似度的均值與方差。GSC的取值在0～1之間，數值越大則代表重構精度越高。

2 RAT矩函數對仿真模型的振型描述與去噪分析

為了驗證RAT矩函數對三維曲面機匣的模態振型描述能力與抗噪性，以一個三維曲面結構的有限元模型為例，材料采用GH4169高溫合金，結構的彈性模量E為204GPa，密度為8240kg/m3，泊松比為0.3。在ANSA中使用二階四面體單元對機匣劃分網格，共有26195個節點，12851個單元。使用Nastran求解器對該模型進行模態計算，計算自由-自由狀態下的前10階模態。

2.1 RAT矩函數對的振型描述能力

圖1 曲面機匣有限元模型

建立的有限元模型見圖1。將振型數據插值到一個圈數×點數×層數的三維像素空間內，構建其模態振型圖。構建的前8階模態振型圖見圖2。利用RAT矩函數對該有限元模型的振型數據進行矩變換，得到每一階模態的特征矩集，每一階的特征矩集見圖3。利用提取出的RAT特征矩集可以對振型圖像進行重構，重構振型圖見圖4。

觀察原始振型圖與利用RAT矩函數重構的振型圖，可以看到重構振型圖的精度非常高，與原始振型圖基本一致，證明了RAT矩函數對三維曲面結構模態振型圖的描述能力。

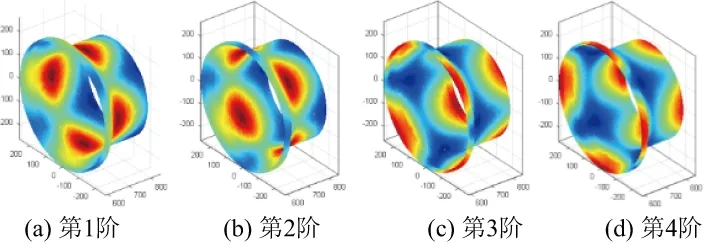
圖2 有限元模型的前8階模態振型

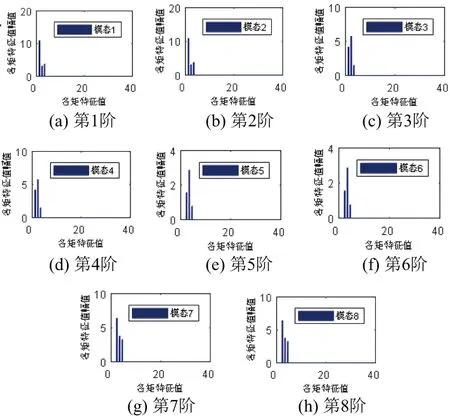
圖3 每一階的特征矩集幅值

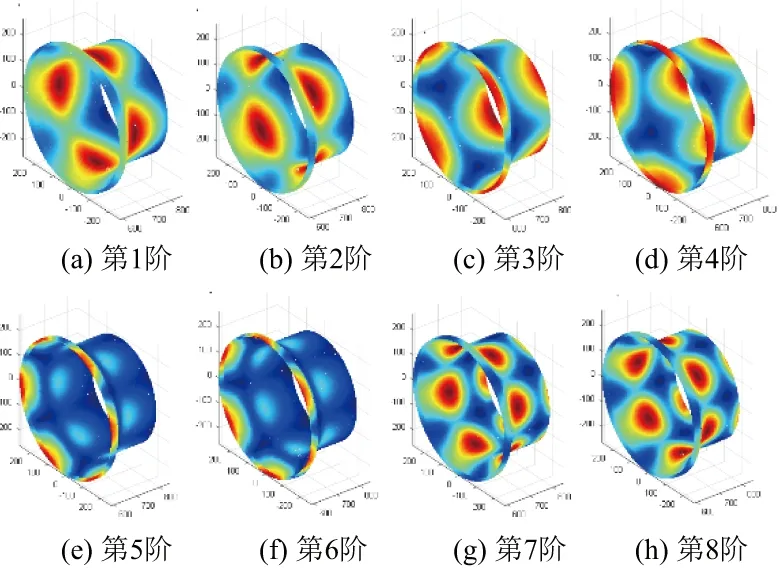
圖4 前8階模態重構振型圖

2.2 RAT矩函數的去噪分析

在有限元模型的振型數據中加入正態分布的隨機噪聲，以達到一個模擬實際情況下噪聲的效果。在此引入一個系數NIF(noise intensity factor)，表示正態分布的隨機噪聲的強度，NIF值為0.5代表強度為50%的隨機噪聲。再通過前文介紹的總體相似系數GSC來表示基于RAT矩去噪后的振型圖像與原始振型圖像的相似度，從而評價RAT矩函數的抗噪效果。在NIF值從0.1～1的情況下，分別計算出每一階模態下加噪聲的振型圖像與原始振型圖像的GSC均值與基于RAT矩去噪后振型圖像與原始振型圖像的GSC均值，將兩條GSC隨NIF值變化曲線繪制在同一張圖中，見圖5。

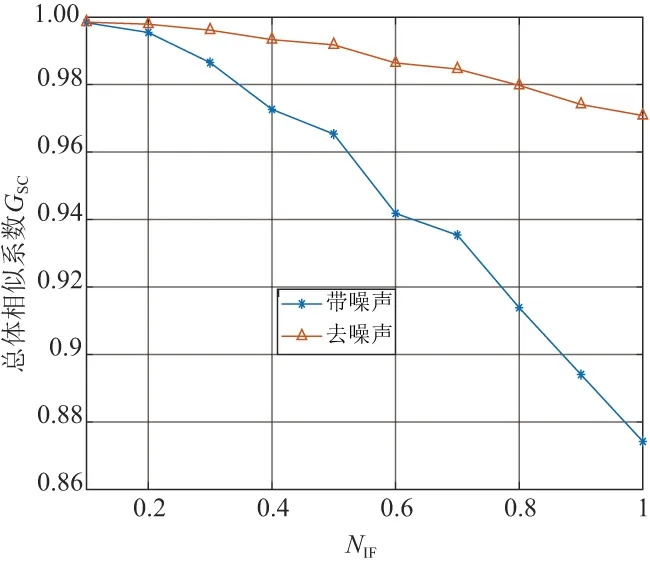
圖5 不同噪聲強度下去噪前后的GSC值

從圖中可見，隨著加入的噪聲強度越來越大，帶噪聲的振型圖像與原始圖像的差別越來越大(GSC值越來越小)，當NIF為1也就是加入100%強度噪聲時，帶噪聲的振型圖像與原始圖像的GSC降低到了0.87。而基于RAT矩去噪后的振型圖像與原始圖像的相似度雖然也隨著NIF值的增大而減小，但是減小的速率非常小，能保持一個穩定性。即使噪聲強度NIF為1的情況，去噪后振型圖像的相似度GSC也在0.97以上，可以證明RAT矩函數能很好地應用在去噪過程中。

再將NIF為1情況下每一階模態下帶噪聲與去噪聲振型圖像與原始圖像的GSC值進行對比，對比圖見圖6。

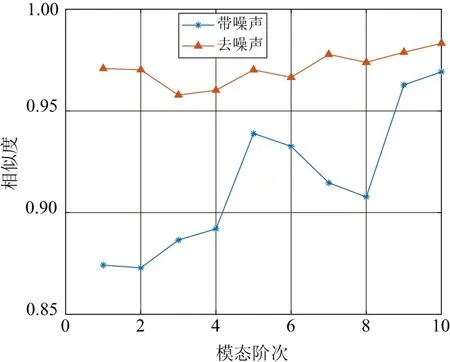
圖6 NIF為1時各階模態去噪前后振型圖的GSC

可以看到，當噪聲強度為100%時，使用RAT矩去噪后振型圖像的相似度始終保持在0.95以上，這也在此驗證了RAT矩函數的去噪能力，即使在噪聲比較大的情況下，依舊能保證去噪后振型圖與原始振型圖有很高的相似度。

最后以第8階模態的振型圖像為例，在NIF值為0.2、0.5、1的情況下，列出第8階模態的原始振型圖、加噪振型圖與去噪后的振型圖對比。NIF為0.2、0.5和1時振型圖像對比見圖7。

由圖7可以看到, 噪聲強度系數NIF值為0.2時去噪后的振型圖和原始振型圖無太大差別，去噪效果十分顯著，NIF值為0.5時去噪后振型圖與原始圖像的相似度相比于NIF為0.2的情況要低一些，但通過振型圖像對比可以看到去噪效果依舊很好。當NIF值為1時，可以看到去噪后的振型圖像與原始振型圖像的相似度有所降低，但是仍具有良好的去噪效果。

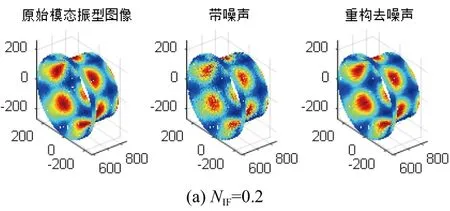
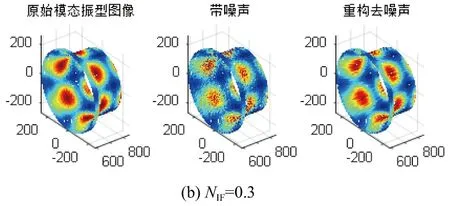
圖7 不同噪聲強度下第8階模態去噪效果圖

3 結語

本文研究了RAT矩函數對三維曲面結構的模態振型描述能力,并且進一步研究了RAT矩函數的去噪效果,得到以下結論：

1) 證明了使用RAT矩函數能夠精確地描述三維曲面結構的模態振型,對進一步將RAT矩用于三維曲面結構的模型修正有重要的意義。

2) 驗證了RAT矩函數的去噪能力,結果顯示在各個噪聲強度下利用RAT矩函數重構模態振型的去噪效果都十分明顯,若將其應用在工程中能有效地解決試驗過程中噪聲影響的問題,具有一定的工程意義。