某型壓氣機的S2流面靜葉調節優化

孫鑫宇，王英鋒，李劭怡

(南京航空航天大學 能源與動力學院，江蘇 南京 210016)

0 引言

航空發動機的設計與優化一直是航空發動機研究的重點。近年來，隨著CFD技術的發展和計算機性能的提升，可以通過運用軟件計算結合實驗的方法進行研究，從而減少了成本[1-2]。當前對CFD的主要應用集中在壓氣機優化及流場分析、壓氣機氣動特性分析等方面[3-7]。壓氣機氣動設計優化體系經歷了從一維設計、二維設計，再到三維設計的發展過程[8]。氣動優化結合CFD技術在壓氣機設計過程中起到了重要的作用[9]。

壓氣機的內部流動十分復雜，不僅是非定常的，而且具有邊界層的作用。描述壓氣機的內部流動，通常需要假定：1)氣體在壓氣機中的流動是定常的；2)氣體在壓氣機內的流動是絕熱的；3)忽略計算面的黏性力，但考慮黏性力對氣流參數的影響；4)流場不存在激波間斷面[10]。

為了簡化求解葉輪機械的三維問題，1952年，吳仲華教授提出了S1、S2流面理論，將三維流場分解為一維與二維計算，為三維流場計算與CFD的發展提供了理論基礎。 20世紀60年代以后，這一理論被廣泛應用于壓氣機、燃氣輪機、透平等葉輪機械的設計優化與流場計算分析。

基于某一工況設計的壓氣機，需要具有在其他轉速與工況下快速響應的能力。因此，對壓氣機的工作特性進行優化，也是當前較為熱門的壓氣機研究方向。常用的方法包括級間放氣、靜葉調節、可變通道面積、多轉子等方法。在這些擴穩方法中，對于針對某些特定工況設計的軸流壓氣機，需要在流場發生變化時具有快速調節的能力。靜葉調節作為擴大壓氣機穩定范圍十分有效且經濟的手段，研究靜葉調節對軸流壓氣機性能的影響是至關重要的[11-13]。

因此，本文基于某型三級壓氣機，結合一維、二維和三維計算，并以S2流面計算為主，對壓氣機各級徑向特性參數分布進行優化。分別對壓氣機的各級總體參數和沿徑向參數進行計算與分析，并結合分析結果進行靜葉調節，對靜葉調節前后的結果進行分析與比較[14-15]，從而提出一種結合部件匹配的靜葉調節優化方法。

1 壓氣機模型設計

如圖1所示的三級壓氣機模型，共有6排葉片，各級靜葉均可獨立調節。為研究壓氣機在不同轉速下、工況下的工作性能，取多組換算轉速值。表1為設計狀態下壓氣機工作時的參數列表。

圖1 三級壓氣機模型

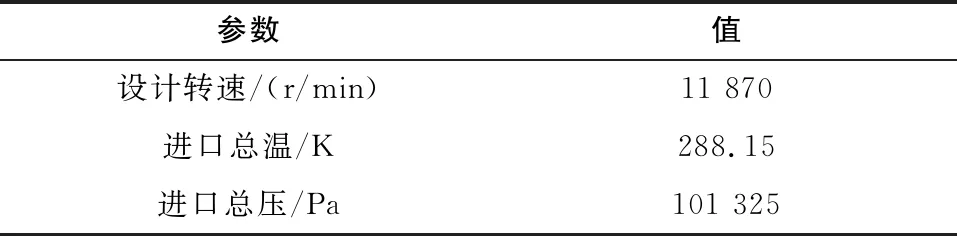
表1 壓氣機設計狀態工作參數

2 研究方法

本文提出的靜葉調節優化方法結合了一維總體參數計算、二維沿徑向各級參數計算、三維CFD數值模擬流場計算驗證，結合流量平衡規律和部件匹配規律，參考了常用的壓氣機設計與優化方法，并基于多組壓氣機計算與優化結果，提出了結合多種約束調節的靜葉調節優化方法，如圖2所示。

圖2 靜葉調節優化方案流程圖

1)一維計算在這一整體優化過程中有著重要的作用。基于Matlab軟件編寫程序，計算多級軸流壓氣機一維氣動參數，基于各級的設計參數和給定的進出口參數，計算各級轉靜子進出口截面平均半徑上的參數；由上述各級的參數計算得出單級的級特性。在得到單級特性結果后，從前向后逐級疊加計算出全臺壓氣機的總特性[16]。通過對一維特性的分析，可以對壓氣機的各級參數分布情況有初步的了解，并為后面的S2與三維計算和靜葉調節方案提供依據。

2)S2流面計算與優化。基于一維計算結果，結合壓氣機幾何參數，計算出壓氣機沿徑向的參數分布。通過對徑向流場參數分布的進一步分析，初步得出壓氣機靜葉調節方案，并重復一維與二維計算過程，對結果進行分析，直到優化結果滿足優化設計要求[17]。

3)三維CFD數值計算驗證。對經過一維與二維計算及靜葉調節的壓氣機進行建模，對優化前后的多級軸流壓氣機性能以及流場特性進行驗算并比較與分析。結合一維與二維計算的優化結果，運用模擬軟件計算壓氣機在靜葉調節前后的工作特性以及壓氣機與渦輪共同工作特性的變化[18]。三維計算通過NUMECA系列軟件的Fine模塊，采用k-ε模型求出定常解，轉捩模型運用AGS模型。同時采用多重網格法等加速計算收斂。

計算中邊界條件給定如下：進口給定總溫、總壓，出口給定靜壓、軸向進氣。計算取多組換算轉速值，并結合共同工作規律計算壓氣機渦輪共同工作的共同工作特性線。

3 壓氣機特性計算結果及分析

對原型壓氣機取多組折合轉速值。對每一折合轉速值取多組工作點，結合壓氣機幾何數據，輸入一維程序計算得出總體參數及各級間參數。通過對一維計算結果進行整理，可以得到通用特性線。對該壓氣機的一維級間特性進行計算，各級轉子的做功能力影響壓氣機整體特性。

圖3為一維計算壓氣機各級的總壓分布。在壓氣機中，轉子轉動推動氣流，對氣流做功，增加氣流的總壓。由圖可得，氣流在經過第一級葉片時有較高的壓比，說明第一級做功量較大，可以通過靜葉調節優化提高后面級的做功量。且后面級壓比與前面級相比明顯較低，說明壓氣機做功分布不均勻，既影響壓氣機整體的做功能力，也影響壓氣機的穩定裕度。

圖3 靜葉調節前各級轉子總壓比分布曲線

對壓氣機葉片S2流面特性進行分析，見圖4、圖5。主要分析各級轉子沿徑向的載荷分布。這些參數主要反映壓氣機各級葉片的做功能力。各級轉子葉片總壓沿徑向逐漸提高，在葉尖處最高。沿軸向前面級作功能力明顯高于后面級，與總壓比分布相對應。可以嘗試通過靜葉調節方法，改善壓氣機葉片的載荷分布，從而改善壓氣機的工作狀態。

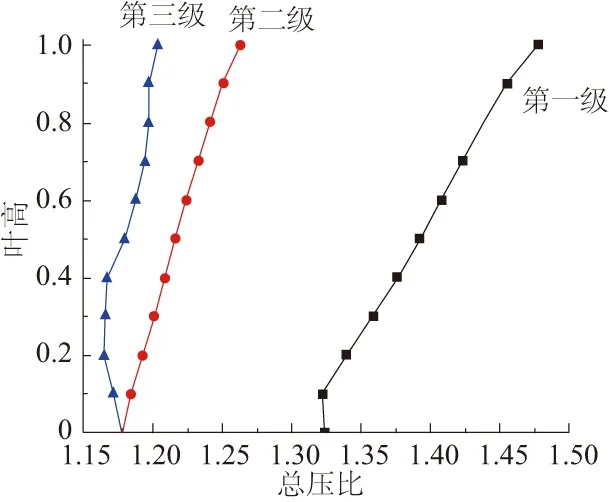
圖4 調節前各級轉子沿徑向總壓比分布曲線

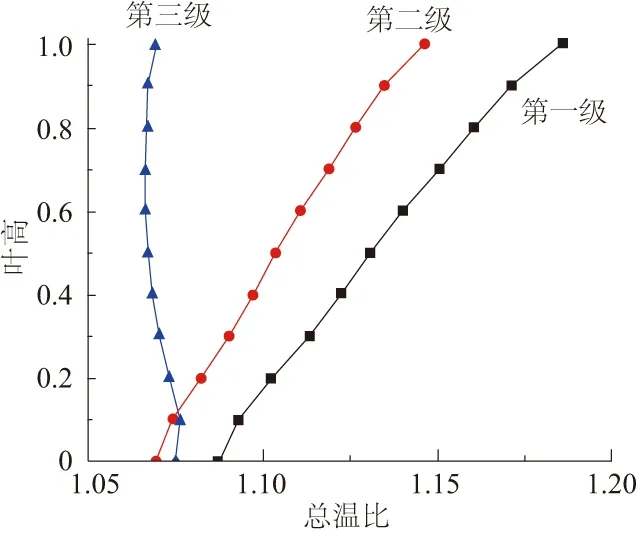
圖5 調節前各級轉子沿徑向總溫比分布曲線

4 靜葉調節壓氣機計算結果及分析

通過對壓氣機一維、二維流場參數的計算分析，對壓氣機進行靜葉調節優化，通過對比確定了最佳的靜葉調節方案。對靜葉調節后的壓氣機進行一維計算，可以得出其轉子進口相對氣流角、級總壓分布等參數。與靜葉調節前的壓氣機參數對比：經過靜葉調節，壓氣機的一維特性得到了優化；第二級壓比得到了一定提高。由圖6可得，通過靜葉調節，第二級的壓比增加，說明靜葉調節改善了壓氣機沿徑向的載荷分布，壓氣機的一維特性得到優化，使總體壓比增加。不僅提高了總體壓比，也降低了第三級通過靜葉導致的總壓損失。圖7為靜葉調節前后的轉子進口總溫比比較。經過靜葉調節，第二級轉子的總溫比都有一定程度的提升。說明經過靜葉調節，使壓氣機具有更好的載荷分布，提高壓氣機的裕度。

圖6 調節前后各級壓力分布曲線

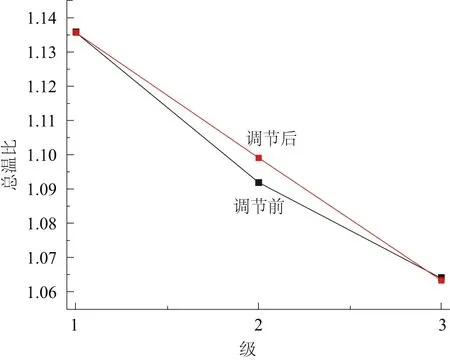
圖7 調節前后各級轉子進口總溫比

對靜葉調節前后的S2流面特性與靜葉調節前進行分析。見圖8、圖9。圖8為靜葉調節前后各級轉子沿徑向的總壓比分布對比圖。由圖可得，經過靜葉調節，除第一級轉子以外，沿徑向壓氣機各級轉子葉片的總壓比有一定的變化。第一級轉子的總壓比沒有變化，第二級轉子的總壓比提高，而第三級轉子的總壓比均值降低，但總壓比分布梯度降低，改善了第三級轉子的載荷分布。圖9為各級轉子沿徑向總溫比分布。顯然，經過靜葉調節，各級轉子的溫升也有一定的變化，經過靜葉調節，第二級轉子的總溫比均值提高，第三級轉子的總溫比分布也更加合理，可以減少一定的損失。結合圖8，沿徑向第二、第三級轉子總壓損失均有明顯降低，說明靜葉調節不僅提高了各級轉子的做功能力，也一定程度減小了損失，從而進一步提高了壓氣機整體的做功能力與效率。

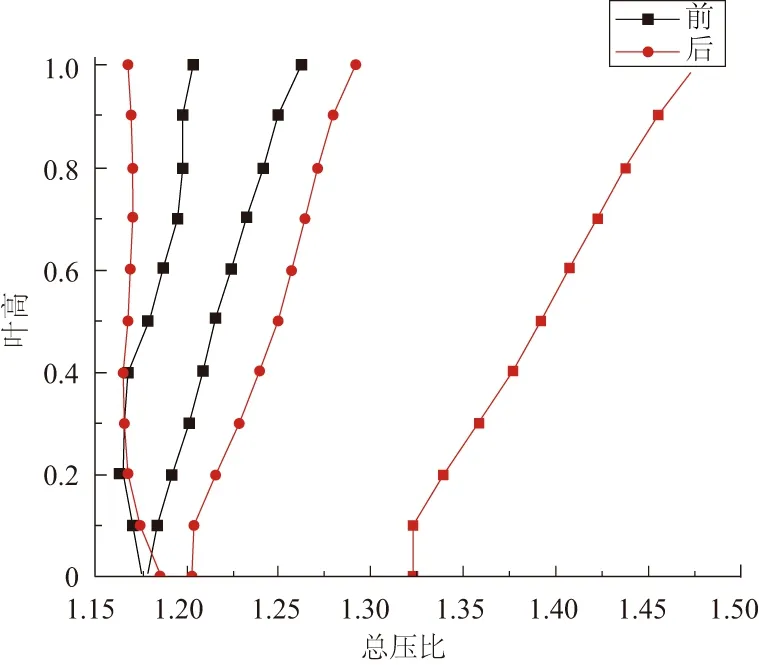
圖8 調節前后各級轉子總壓比沿徑向分布

圖9 調節前后各級轉子總溫比沿徑向分布

5 三維計算結果的驗證與對比

通過結合壓氣機的一維、二維計算結果對壓氣機進行靜葉調節優化結果對比分析，可以初步得出，經過靜葉調節，壓氣機的載荷沿軸向與徑向的分布得到了一定的優化，且內部流場也可得到一定的改善。但對于壓氣機整體的工作特性以及各級與徑向特性參數分布，需要結合三維CFD計算進行驗證。

圖10顯示了靜葉調節前后子午面壓力分布情況。沿流程，總壓不斷增加。通過靜葉調節，壓氣機后面級的總壓有一定的升高，且壓氣機的子午面總壓分布也得到了優化，第二級轉子葉尖處的局部高壓區得到了減小，且最后一級的總壓分布也有明顯的優化。體現了靜葉調節對總壓分布的優化。

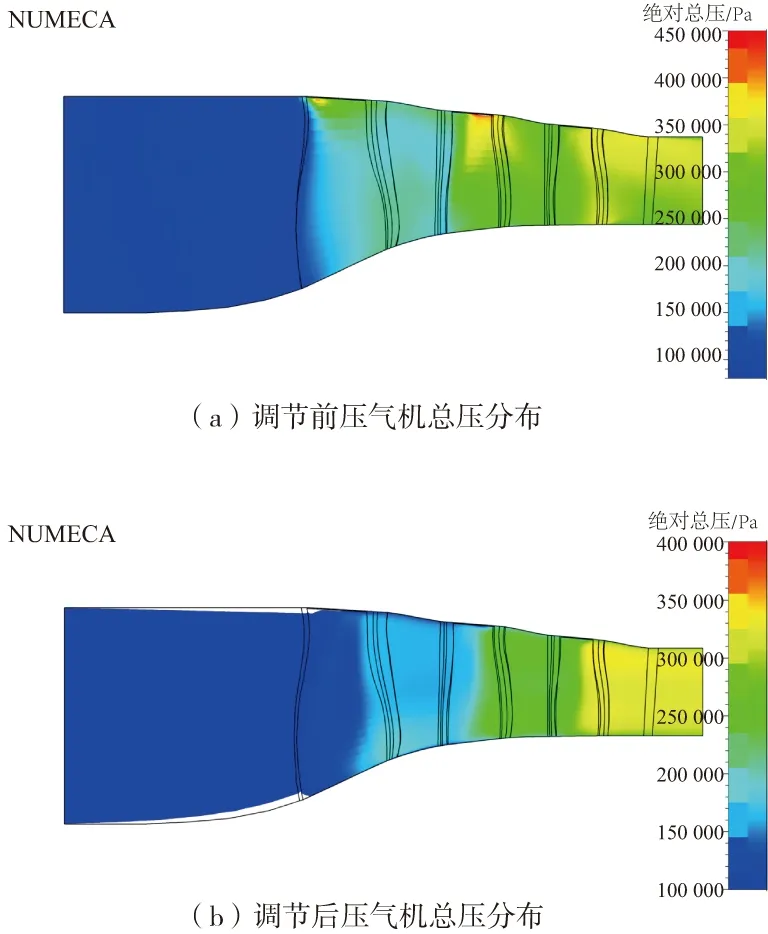
圖10 靜葉調節前后壓氣機總壓子午面分布

圖11顯示了改型靜葉調節前后壓氣機沿軸向的總溫分布情況。與壓力分布相似，總溫與靜溫整體沿流程也是逐級增加。經過靜葉調節，第二級轉子的總溫均值有一定的提升，說明第二級轉子的做功能力增強。

圖11 靜葉調節前后壓氣機總溫分布

6 結語

本文基于壓氣機的工作規律，結合一維、二維和三維計算方法，通過對三級壓氣機進行靜葉調節優化，并對優化前后的計算結果進行分析比較，得到以下結論：

1)通過一維與二維計算，對壓氣機靜葉進行調節，可以實現靜葉調節后穩定裕度提高，提高了其穩定工作范圍。通過對壓氣機的靜葉進行調節，并對計算結果運用一維計算進行壓氣機級進行計算，運用S2流面計算方法進行各級徑向參數計算，最后進行三維計算驗證，確定了這種基于多種規律的靜葉調節方法可以改善壓氣機在近失速點的流場參數分布。

2)本文中提出的靜葉調節優化方法，對壓氣機的單級特性、總體特性均進行了一定程度的優化，提高了壓氣機的做功能力，對航空發動機整體優化的分析計算具有一定的實際應用價值。

3)通過文中對壓氣機的基于S2流面計算的參數分析及優化，為靜葉調節優化方法提供了一定的思路。結合優化算法、神經網格等方案對壓氣機進行進一步精確的優化，可以進一步提高計算精度并得到更加可靠的優化結果。