基于正交試驗和神經網絡的液壓桿穩定性研究
易 帥,孫巧雷,馮 定,周 蘭,靳祖文
(1.長江大學 機械工程學院,湖北 荊州 434023;2.湖北省油氣鉆完井工具工程技術研究中心,湖北 荊州 434023;3.非常規油氣湖北省協同創新中心,湖北 武漢 430100)
引言
液壓桿位于動力貓道翻板處,當動力貓道在自動上、下管柱至鉆臺時,液壓桿會受到較大的載荷作用,當載荷超過液壓桿的臨界載荷時,液壓桿就會發生穩定性失效,可能導致鉆井事故的發生,影響石油天然氣的勘探開發,造成人員和經濟的損失[1]。因此,有必要對液壓桿的穩定性進行研究。SYSOEV A S等[2]對變剛度可壓縮可彎曲剛性桿的穩定性問題進行了研究和解決,建立了桿件臨界載荷的帶根超方程體系;CAI Yong等[3]在考慮初始缺陷對桿件的影響的同時,采用了近似解法和穩定周期解的傅里葉法,從理論上分析了周期瞬態荷載作用下桿件的動力穩定性,通過對桿件不同撓度的研究,用Maple軟件計算了桿件的動力不穩定性;LEONID K等[4]提出了一種利用數值解析的邊界元法(MGE)求解連續梁等桿系穩定性問題的算法,并在MATLAB環境下進行了臨界力的計算;馮超等[5]利用有限元軟件對受壓桿件的穩定性進行分析,并對其臨界載荷進行了ANSYS驗證;李琳等[6]以Koiter穩定性理論為研究基礎,分別分析了不同約束的壓桿在歐拉臨界載荷作用下的穩定性;周奇才等[7]基于壓桿穩定性定義,在歐拉描述方式下提出了一種軸向剛度判別法,通過對剛架模型進行數值分析,驗證了該軸向剛度判別法的有效性和適用性;包衛平等[8]從強度和壓桿穩定的觀點對升降桅桿進行彎曲強度和壓曲穩定性分析,采用能量法和等效剛度法推導出變截面壓桿的剛度求解公式。
國內外學者對受壓桿件的穩定性進行了廣泛的理論計算分析和有限元仿真模擬[9-14]。但在實踐過程中發現:由于環境因素的影響,會在液壓桿上產生缺陷,如圖1所示,缺陷使液壓桿發生彎曲破壞的臨界載荷減小,更易發生穩定性失效。所以本研究針對含有缺陷的液壓桿分析了影響壓桿穩定性的因素,并利用正交試驗法得到了各個因素對液壓桿穩定性的影響趨勢及其顯著性,同時利用BP神經網絡建立了液壓桿屈曲載荷預測模型,為含缺陷的液壓桿在使用過程中的穩定性提供比較準確的預測,以減少事故的發生。

圖1 液壓桿上的缺陷
1 液壓桿有限元計算模型
根據桿端位移的歐拉公式[15],當液壓桿的材料和使用工況確定后,液壓桿的屈曲載荷大小取決于液壓桿最小截面慣性矩。液壓桿最小截面慣性矩與缺陷的形狀、深度、位置以及缺陷的面積有關,為了得到不同缺陷因素對液壓桿穩定性的影響規律與影響顯著性,有必要對液壓桿進行數值模擬來研究缺陷與液壓桿穩定性之間的關系。液壓桿上出現的缺陷形狀一般是不規則的,數值模擬時將缺陷的表面規則化處理為圓、橢圓、矩形。
1.1 模型建立
建立的液壓桿三維模型如圖2所示,材料為42CrMo,其密度為7850 kg/m3,彈性模量為206 GPa,泊松比為0.3,中間部分直徑為12 mm,長度為150 mm。對現場使用的液壓桿缺陷進行測量與記錄,選取缺陷的深度為0.8,1.6,2.4,3.2,4.0 mm;缺陷的面積為4.5,8,12,18,25 mm2;缺陷距底端的距離為35,65,75,85,115 mm。以此為基礎建立液壓桿的有限元模型,對不同缺陷的液壓桿臨界載荷進行了有限元計算。

圖2 液壓桿三維模型
1.2 網格劃分及邊界條件與載荷
運用靜態結構模塊和線性屈曲模塊對液壓桿的臨界載荷進行求解,將建立的液壓桿三維模型導入有限元軟件中,采用四面體單元對結構進行網格劃分,由于模型的計算對計算機內存要求較高,所以網格數不宜過密,經網格無關性檢查,最終的網格數約為24萬,不同類型缺陷局部細化網格如圖3所示。根據實際工作狀況對液壓桿進行約束,即對液壓桿的底端進行固定約束,上端施加一軸向的壓力,液壓桿約束與受力如圖4所示。由于有限元軟件計算的臨界載荷為加載值與屈曲因子的乘積,所以在液壓桿上端加單位載荷,有限元分析得到的屈曲因子即為液壓桿的屈曲載荷。

圖3 不同類型缺陷局部細化網格圖
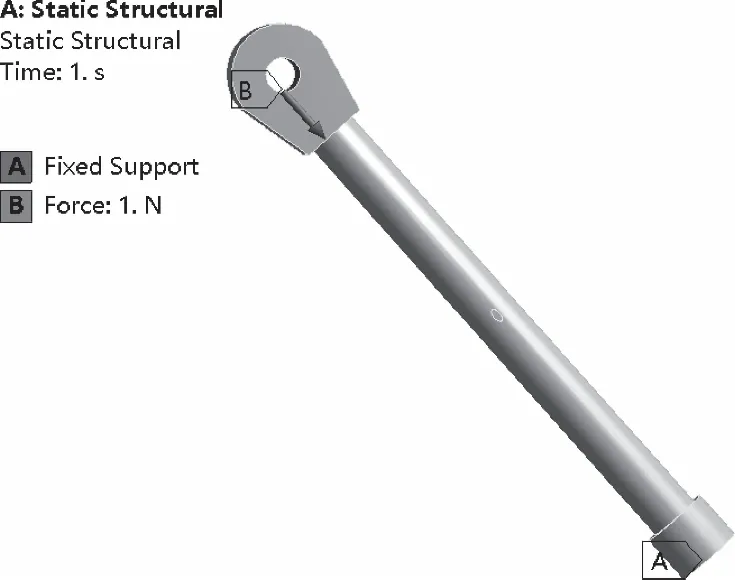
圖4 液壓桿約束與受力圖
2 試驗設計與分析
2.1 正交試驗分析
由于將所有因素全部進行有限元分析需要375次試驗,為了減少試驗次數且不影響試驗的準確性,采用正交試驗的方法對影響液壓桿穩定性的因素進行分析[16]。影響含有缺陷的液壓桿穩定性的因素主要有缺陷的形狀、深度、位置、面積,因此,本研究選取的正交表為L25(3×53),各個因素水平表如表1所示。
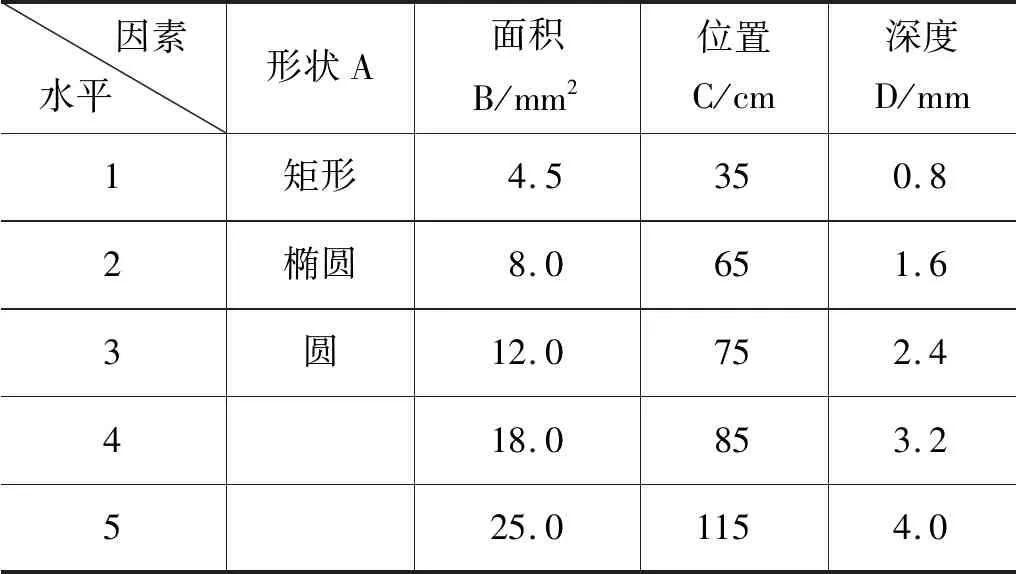
表1 因素水平表
表2為混合正交表,需要進行25次試驗,對每次試驗運用有限元分析軟件計算液壓桿的臨界載荷,試驗方案和有限元計算的結果如表2所示。

表2 試驗方案及分析結果表
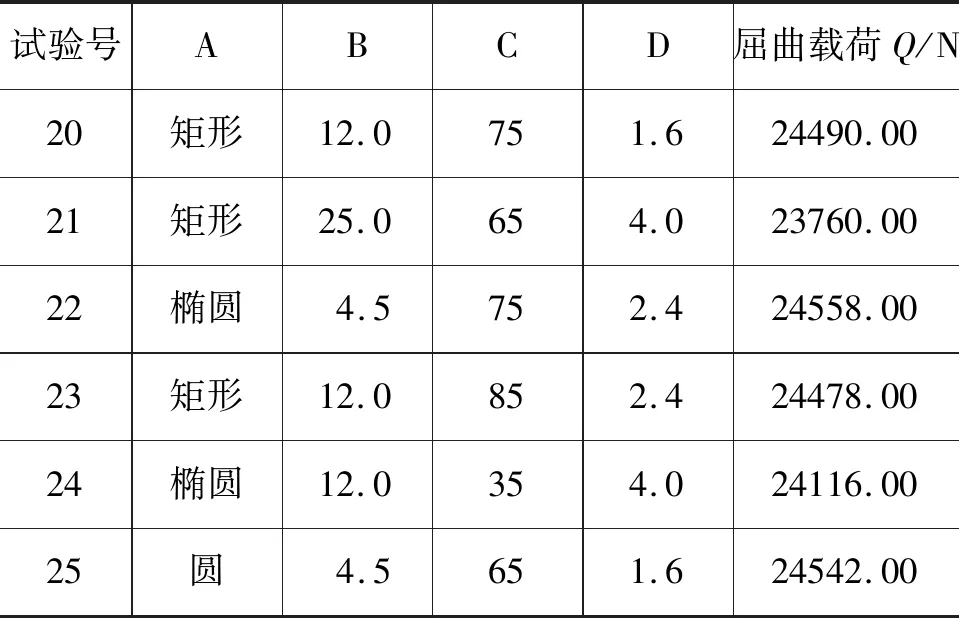
(續表2)
2.2 直觀分析
由于液壓桿的屈曲載荷受4個因素的影響,故需要考慮多目標正交試驗結果的直觀分析。運用直觀分析法對試驗數據進行處理如表3所示。其中,Kij(i=1,2,3,4,5;j=1,2,3,4)表示表1的第j列中水平為i對應的試驗結果之和;kij為Kij的算術平均值;極差Rj=maxkij-minkij。
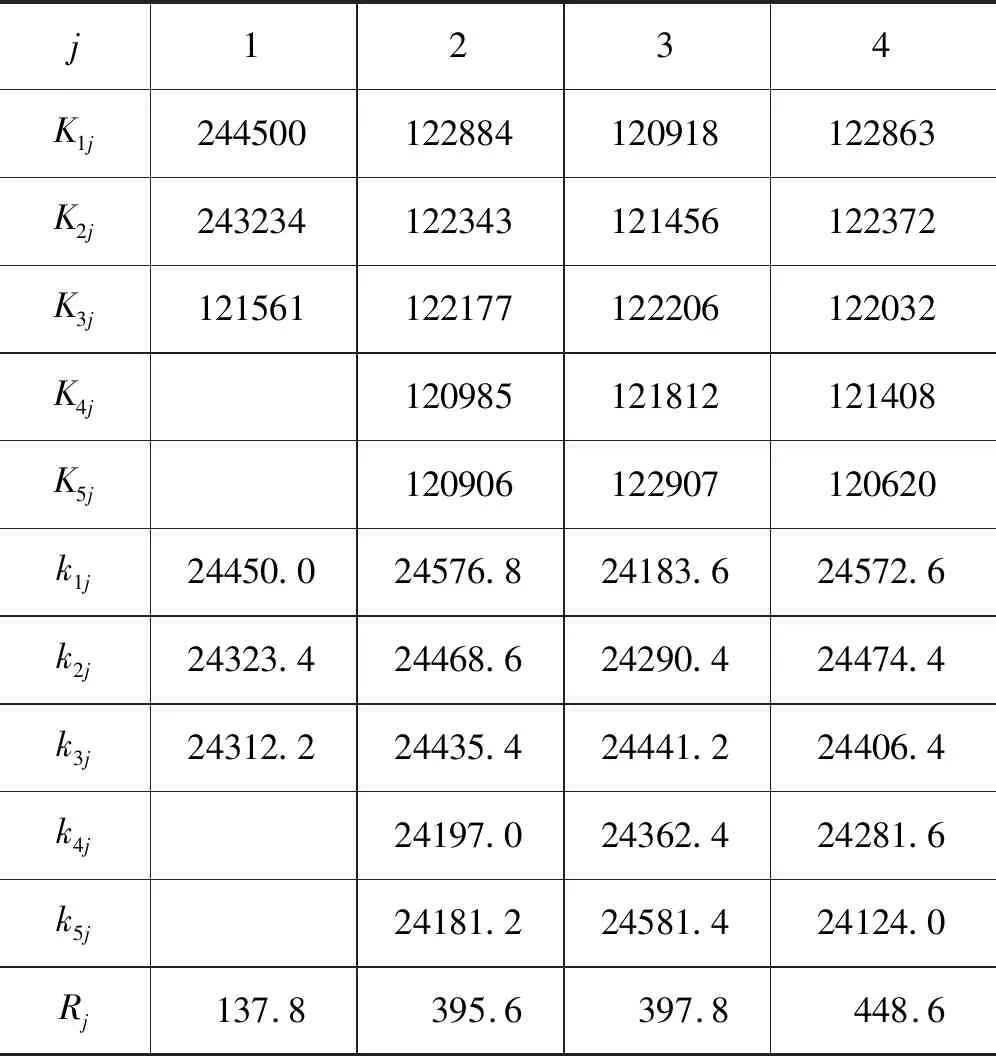
表3 數據分析計算表
極差Rj可以衡量各個因素對試驗指標影響的大小,極差越大,表明這個因素對液壓桿穩性的影響越大。從表3可以看出,缺陷深度、缺陷相對底端的距離和面積所對應的極差較大,故缺陷深度、缺陷相對底端的距離和缺陷面積對液壓桿穩定性影響較大,而缺陷的形狀對液壓桿穩定性影響較小;由于k31
2.3 方差分析
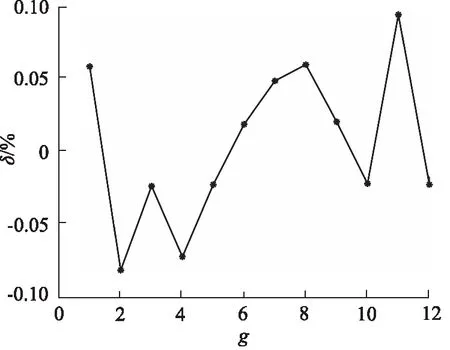
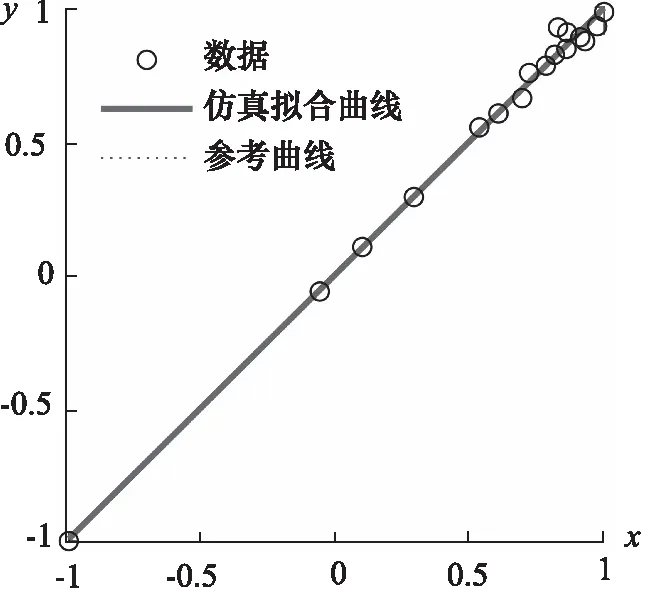
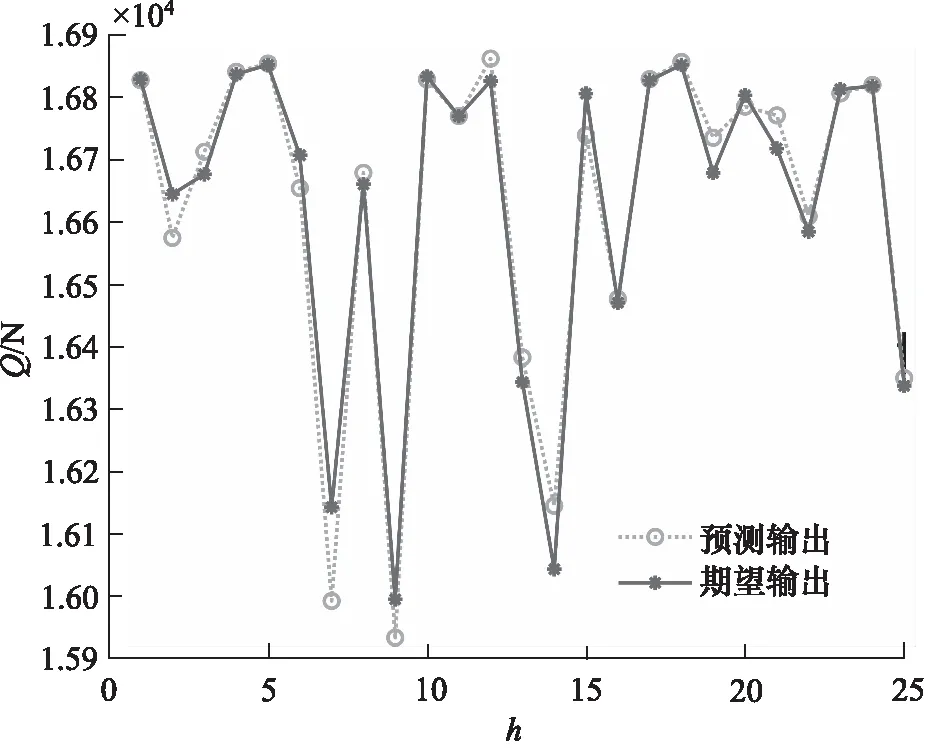
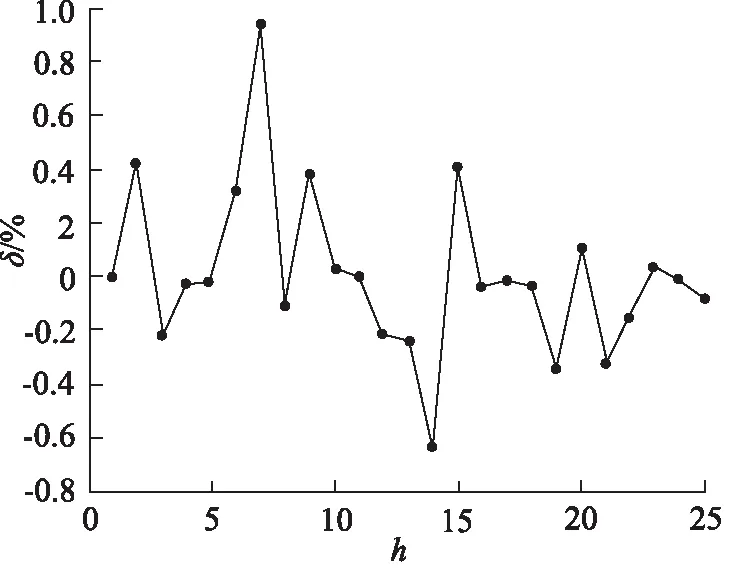
對試驗數據方差分析結果如表4所示,其中,P值表示該因素對結果影響出現不顯著情況的概率,設缺陷形狀、缺陷面積、缺陷位置、缺陷深度的P值分別為P1,P2,P3,P4。若P<0.01時,則表明該因素對試驗結果具有高度顯著影響;若0.01 表4 方差分析表 圖5 液壓桿屈曲載荷預測模型結構圖 基于MATLAB軟件,對液壓桿屈曲載荷的預測模型常用3×3×1×1的BP神經網絡進行訓練與預測。訓練樣本總計37組,將正交試驗中的25組作為學習樣本,將缺陷面積、位置和深度進行單因素分析的12組作為預測樣本。為了使模擬結果收斂且能較好地模擬預測樣本,選擇的神經網絡誤差精度為0.001,學習速率為0.01,訓練次數為1000。BP神經網絡預測輸出與期望輸出如圖6所示,橫坐標為仿真預測樣本序號g,預測誤差δ如圖7所示。 圖6 BP神經網絡預測與期望輸出折線圖 從圖6可以看出,12組預測輸出和期望輸出的變化趨勢一致,預測輸出的12個點在期望輸出12個點附近且數值相差不大。由圖7可知,該神經網絡預測模型的預測值與期望值的誤差在-0.1%~0.1%之間,說明根據正交數據訓練的BP神經網絡具有很高的精確度。 圖7 BP神經網絡預測誤差百分比 如圖8所示,在液壓桿屈曲載荷的BP神經網絡擬合表征中,橫坐標為預測值x,縱坐標為實際值y,在神經網絡訓練時將數據進行了規范化,使預測值與實際值在-1~1之間。參考曲線代表預測值與實際值相等,擬合曲線的斜率為R,R值為預測輸出與期望輸出的相關系數,R值越接近1說明預測輸出與目標輸出的相關性越大,即神經網絡預測模型的擬合程度越高,擬合曲線表達式為y=0.99754x+0.0031,則該液壓桿屈曲載荷預測模型的相關系數R=0.99754,表明該BP神經網絡預測模型能夠對液壓桿屈曲載荷進行很好的擬合,利用該神經網絡對出現缺陷的液壓桿屈曲載荷進行預測是可行的。 圖8 BP神經網絡誤差擬合結果 為了深入驗證模型的正確性,應用本研究的BP神經網絡模型,對參考文獻[20]相關數據進行驗證和分析。該文獻研究了含缺陷液壓桿的屈曲載荷和缺陷的面積、位置和深度間的關系,基于該文225組實驗數據,將200組作為訓練樣本,25組作為預測樣本,對建立的BP神經網絡進行訓練,訓練結果如圖9、圖10所示,橫坐標為實驗預測樣本序號h。 圖9 BP神經網絡預測與期望輸出折線圖 從圖9可以看出,建立的BP神經網絡模型能夠比較準確地預測含缺陷液壓桿的屈曲載荷,且實驗值與預測值的差值不超過150 N,所以在此范圍內對含缺陷液壓桿屈曲載荷的預測是可行的。由圖10可知,該神經網絡預測值與實驗值的最大相對誤差為1.002%,相對誤差控制在5%以內。表明該BP神經網絡模型對含缺陷液壓桿屈曲載荷的預測精度較高,同時也說明缺陷的面積、位置及深度對含缺陷液壓桿的屈曲載荷有重要影響。 圖10 BP神經網絡預測誤差百分比 (1) 首先根據桿端位移的歐拉公式,得到可能影響含缺陷液壓桿穩定性的因素。運用正交試驗方法和有限元仿真研究了缺陷的結構與尺寸對液壓桿穩定性的影響規律,發現缺陷的面積、位置、深度對液壓桿的穩定性具有顯著影響,且液壓桿的臨界載荷與缺陷面積和深度負相關,與缺陷到底端的距離正相關;缺陷的形狀對液壓桿的穩性影響較小; (2) 通過正交試驗數據建立的BP神經網絡模型對液壓桿屈曲載荷仿真的預測具有很高的精確度,最大相對誤差在0.1%內,且預測輸出與期望輸出相關系數為0.99754; (3) 將建立的BP神經網絡模型通過實驗數據的訓練,最大相對誤差為1.002%,即能夠較準確地對桿件的屈曲載荷進行預測,說明該BP神經網絡能夠運用于現場預測含缺陷液壓桿屈曲載荷,防止液壓桿因載荷過大而屈曲破壞。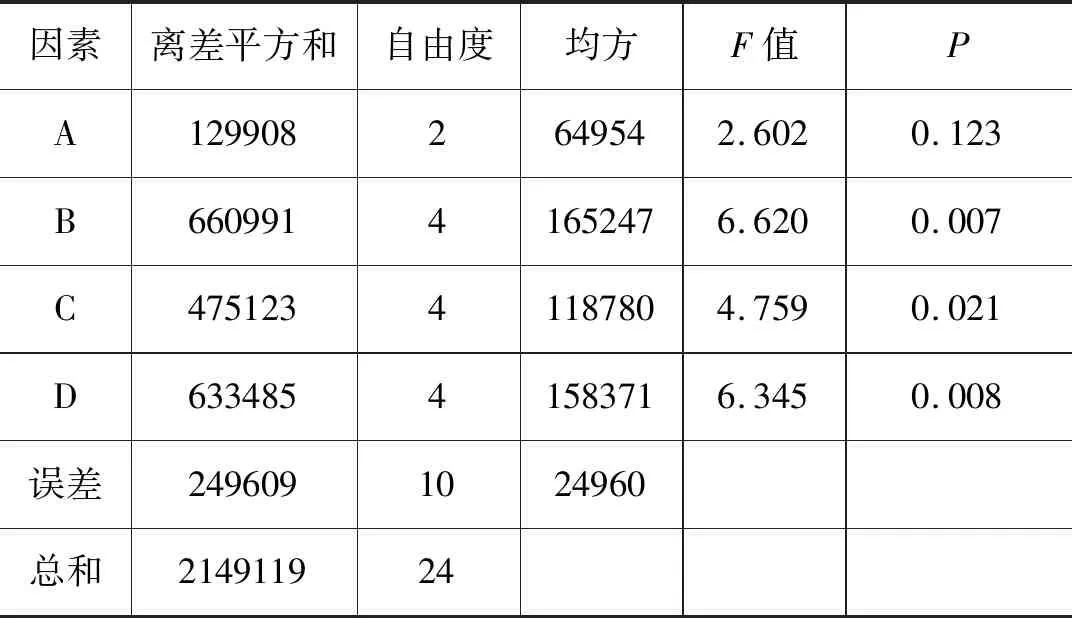
3 液壓桿屈曲載荷預測
3.1 預測模型的選取
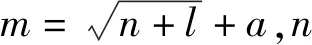
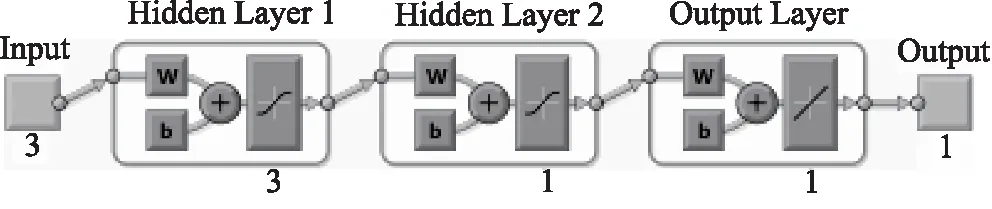
3.2 液壓桿屈曲載荷的預測與檢驗
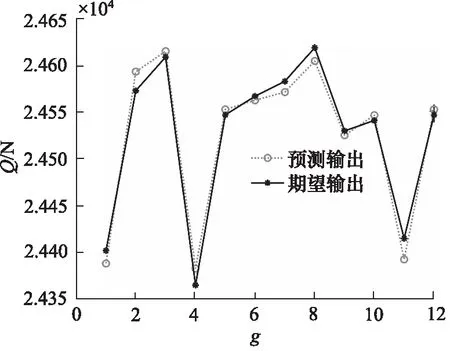
3.3 模型驗證與分析
4 結論

