電液雙缸系統同步控制

張 兵，蔣子良，黃 華，蔡佳敏，謝昌昊，張新星，錢鵬飛

(江蘇大學 機械工程學院，江蘇 鎮江 212013)

引言

當2個以上執行機構共同工作時，需要考慮同步控制問題。液壓同步控制技術具有控制容易、效果好、適配于高功率的應用場所等特點，廣泛應用于工業領域[1-3]。由于電液雙缸系統存在復雜的外界干擾以及較多的非線性因素，研究具有高精度的運動同步控制策略以及有著優良性能的同步控制算法具有重要意義[4-6]。

國內外學者研究了很多同步控制策略，其中，PID控制因其結構簡單、魯棒性強等特點，是應用最廣的控制策略；然而，在變參數和存在外界干擾的情況下，傳統的PID控制魯棒性較差[7]。王磊[8]提出了積分分離PID控制，在偏差大于閾值時選擇PD控制使系統能夠快速響應，在偏差小于閾值時采用PID控制來降低穩態誤差，提高系統穩定性；陳健[9]在大型構件液壓同步提升系統中應用了單神經元的神經網絡自適應控制，并驗證了該控制方法具有比傳統PID控制更好的穩定性；黎良思等[10]在傳統控制方式上加入模糊控制器來實現控制系統參數的在線調整，以提高系統的自適應能力；周育才等[11]設計了一種基于巨型模鍛液壓機主動同步控制系統的魯棒調節器，很好地抑制了系統非線性參數的波動。

本研究建立電液雙缸系統同步誤差的數學模型，提出基于內力補償和位置補償的自由度控制策略，建立仿真模型并進行了靜態和動態驗證，仿真結果表明采用該控制策略能夠實現位置同步和出力的高度一致性。

1 基于自由度控制算法的雙缸位置同步控制建模

液壓雙缸實物圖如圖1所示，當采用兩作動器或多作動器時，兩作動器的同步性既會影響電液雙缸同步控制的精度，又可能破壞負載。因此，結合四通閥控液壓缸基本方程和控制框圖[12]，提出了基于自由度控制算法以實現電液雙缸的同步控制，該控制算法是一種位置交叉耦合和力解耦結合的控制方法，其控制模型框圖如圖2所示。控制框圖內相關符號物理意義見表1。

圖2 基于自由度控制算法的雙缸同步控制模型

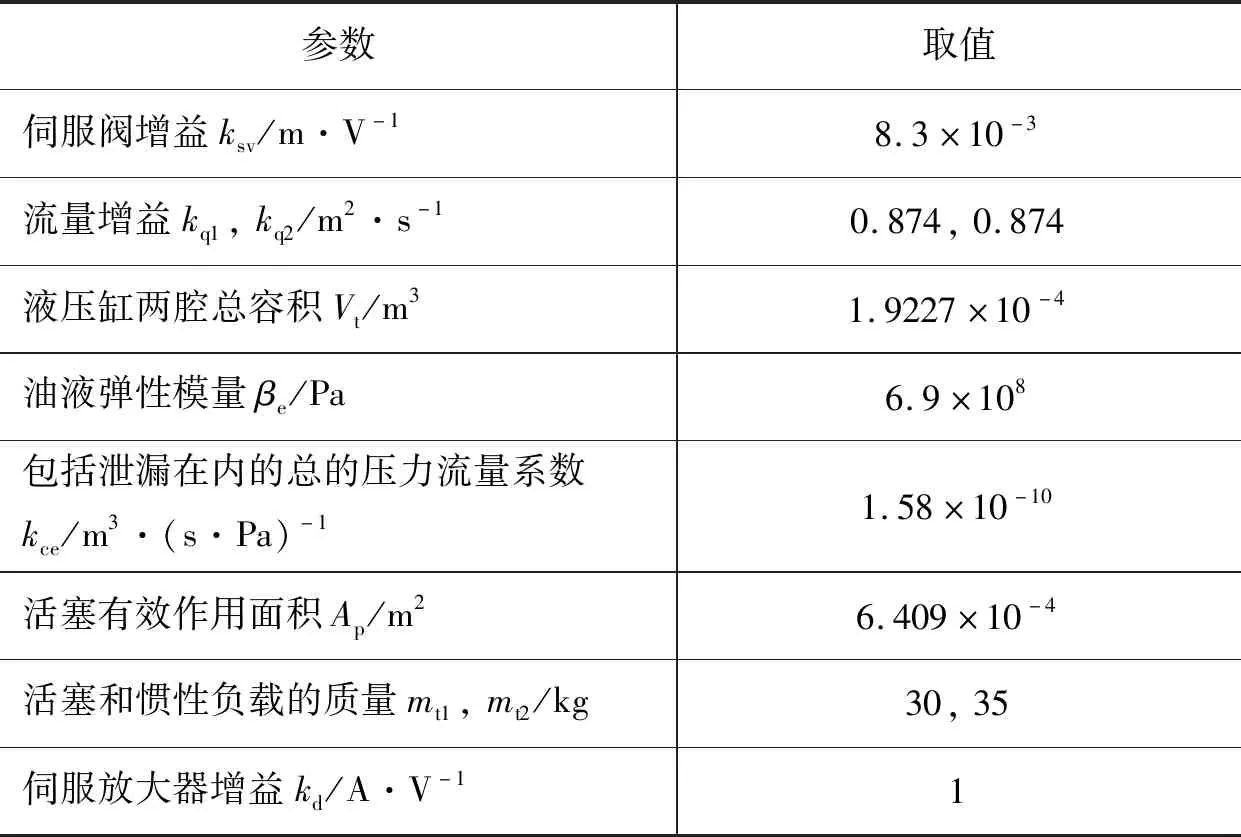
表1 電液雙缸系統中主要相關控制參數

圖1 液壓雙缸實物圖

由于在大多數應用場合，液壓動力元件的負載主要是慣性負載，而沒有彈性負載或者彈性負載很小，故可以忽略，并且負載的黏性阻尼系數Bp較小，也可以忽略[13]。

液壓缸活塞與缸筒之間的相對位移與伺服閥電壓給定信號及內力之間的傳遞函數可以表示為：

(1)

(2)

式中，ωh為系統的固有頻率；ζh為系統的阻尼比U1=U+ΔU，U2=U；ksh1和ksh2為開環增益，ksh1=ksvkq1/Ap，ksh2=ksvkq2/Ap。

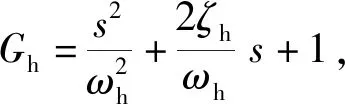
(3)

Fλ=kL(Y1-Y2+ΔYm)

(4)

由式(1)～式(4)，可以得到：

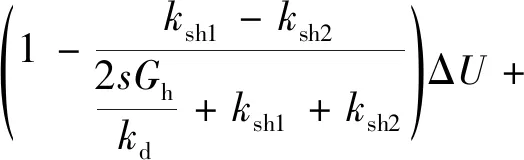
(5)

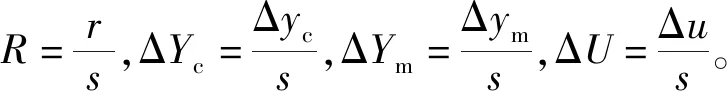
根據拉普拉斯終值定理，穩態時的內力可以用下式計算：

(6)

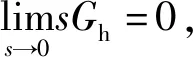
(7)

由式(7)可以看出，在自由度控制策略下，穩態時的內力與液壓缸的安裝誤差Δym、位移的測量誤差Δyc以及負載的剛度kL均無關，其內力的大小主要取決于伺服閥的零偏。由于系統中不可避免存在的各種影響因素都會使2個液壓缸存在同步誤差，即2個液壓缸的位移不同步，使系統試件產生變形內力，該變形內力與系統試件的剛度和同步誤差有關，同步誤差越大，變形內力越大，對試件的破壞作用越大。因此，為了減小對試件的變形內力，可以通過內力積分的方式將系統變形內力補償到系統電壓信號輸入端，從而消除系統變形內力。圖3為加入內力補償后基于自由度控制算法的電液雙缸同步控制系統模型，該模型包括位移交叉耦合和力解耦控制2部分，2部分共同作用能夠保證系統存在各種誤差影響因素情況下，在動靜態時都能夠保證系統無變形內力且保證系統中2個液壓缸的位置同步。

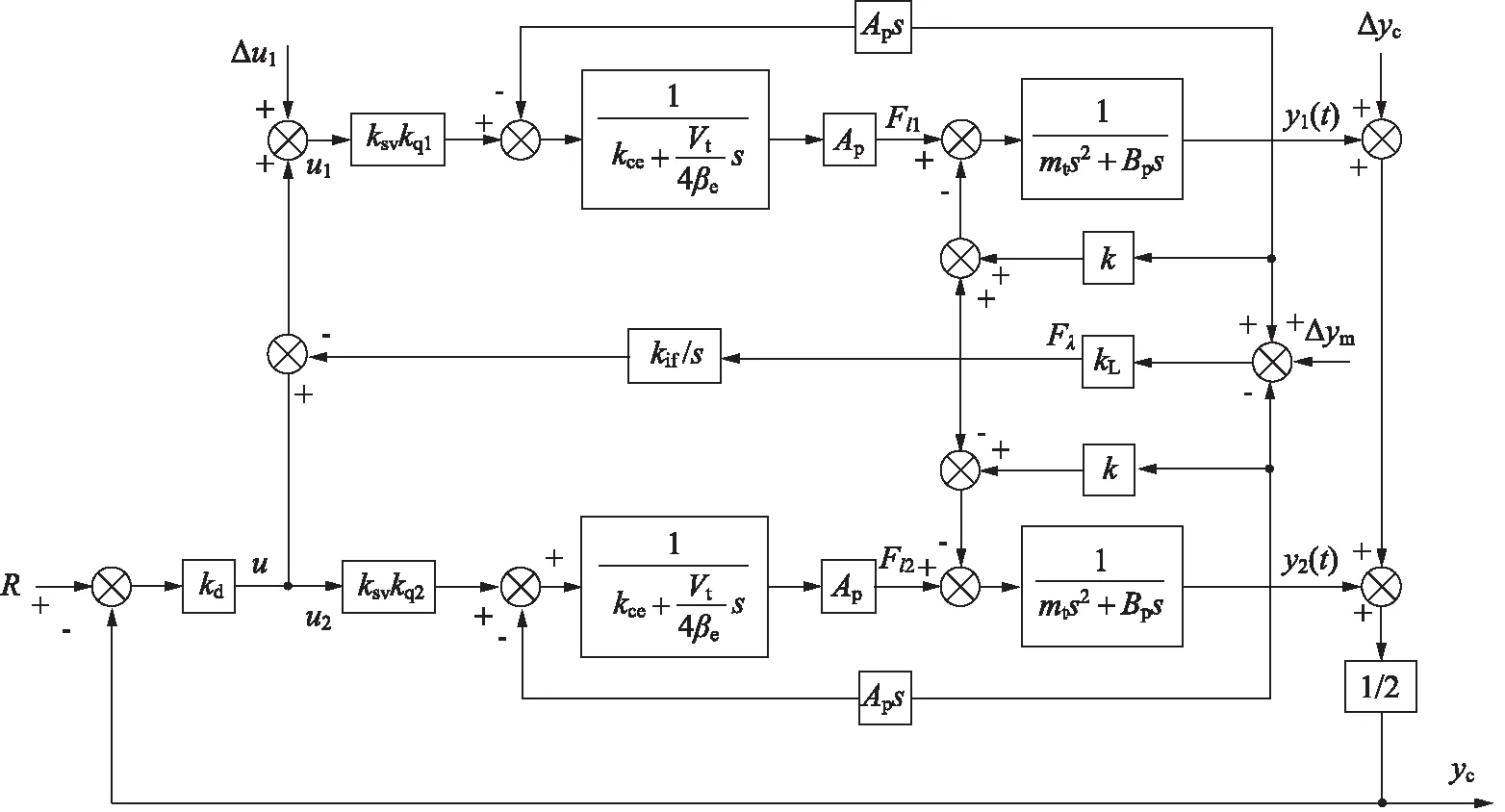
圖3 基于自由度控制算法的雙缸同步控制模型-內力補償

2 雙缸位置同步控制方法仿真分析

2.1 無內力補償

根據圖2所示的控制算法和表1所示的系統中主要相關控制參數，應用MATLAB/Simulink軟件搭建其仿真模型，系統仿真時給定信號為0。仿真分析在無內力補償采用自由度控制算法時，系統的反饋位移和內力與各影響因素的關系。仿真共分為3種工況：只有位移測量誤差、只有機械安裝誤差和只有伺服閥零偏。其中測量誤差Δyc分別為0，1，2 mm，安裝誤差Δym分別為0，0.1，0.2 mm，零偏Δu分別為0.1，0.2，0.3 V，負載剛度kL分別取1×107，2×107，3×107N/m。

圖4為系統存在不同的位移測量誤差時，系統的位移響應信號和系統內力曲線。從圖4a中可以看出，在3種不同測量誤差參數情況下，系統的響應信號快速從位移測量誤差恢復并穩定至系統給定信號，系統的響應時間為0.2 s左右，系統響應較快。此外，從圖4b可以看出，系統加入位移測量誤差瞬間，系統的2個液壓缸內力較大，然后迅速減小并逐漸減小至0，即系統中不存在內力。上述現象說明，采用本研究提出的基于自由度控制算法的同步控制方法時，系統的內力不受系統中位移測量誤差的影響，即系統內力大小與位移測量誤差不相關，從而驗證本研究理論分析正確。

圖4 Δyc對系統響應的影響

圖5為系統存在不同的安裝誤差時，系統的位移響應信號和系統內力曲線。從圖中可以看出，3種誤差參數情況下，系統的位移響應信號快速從位移測量誤差恢復并穩定至系統給定信號。此外，3種情況下系統加入安裝誤差瞬間，系統的2個液壓缸內力非常大，然后迅速減小并逐漸減小至0，即系統中不存在內力。上述現象說明，采用本研究提出的基于自由度控制算法的同步控制方法時，系統的內力不受系統中位移測量誤差的影響，即系統內力大小與安裝誤差不相關。

圖5 Δym對系統響應的影響

圖6為不同負載剛度時，系統的位移響應信號和系統內力曲線。從圖中可以看出，3種不同參數下，系統的位移和內力均為0，從而證明系統內力不受負載剛度的影響。

圖6 kL對系統響應的影響

圖7為系統存在不同的伺服閥零偏時，系統的位移響應信號和系統內力曲線。從圖7a中可以看出，3種誤差參數情況下，系統的位移響應信號分別迅速穩定至0，0.05，0.1 mm，這說明系統位移響應信號與伺服閥零偏相關，并且成線性正比例關系。從圖7b可以看出，3種情況下系統中2個液壓缸內力分別穩定至0，1.5，3.2 kN。上述現象說明，采用本研究提出的基于自由度控制算法的同步控制方法，未加入內力補償控制時，系統的內力和響應信號受系統中伺服閥零偏的影響，即系統內力大小與伺服閥零偏相關。

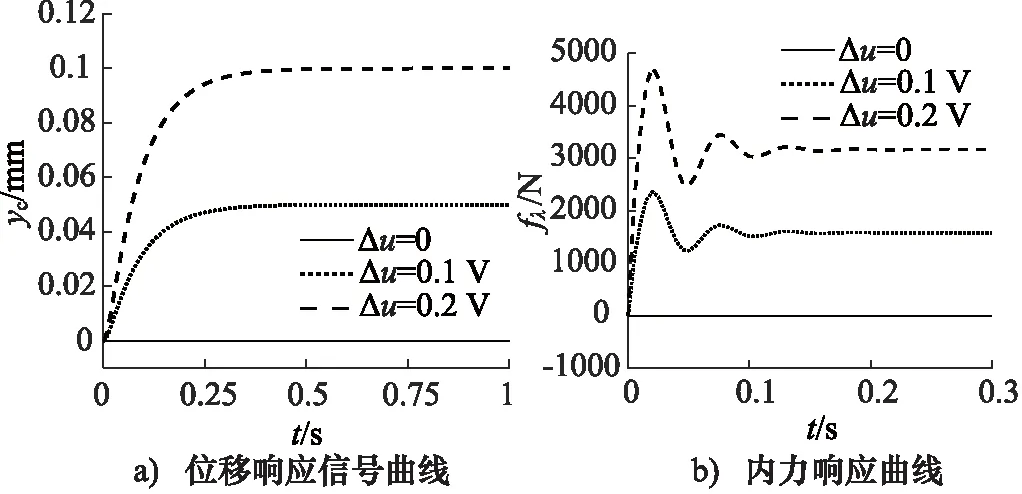
圖7 Δu對系統響應的影響

2.2 有內力補償

根據圖3所示的控制算法和表1所示的系統中主要相關控制參數，應用MATLAB/Simulink軟件搭建其仿真模型，仿真分析在加入內力補償后采用自由度控制算法時，伺服閥的零偏對系統的反饋測量位移和內力的影響。

圖8為系統存在不同的伺服閥零偏時，系統的位移響應信號和系統內力曲線。3種誤差參數情況下，系統的響應信號迅速都穩定至0。從圖8b可以看出，3種情況下系統內力在加入伺服閥零偏瞬間較大，然后迅速衰減并穩定至0。上述現象說明，在加入內力補償控制方法后，系統的位移響應信號和系統內力不再受伺服閥零偏的影響，從而驗證了提出的控制方法的正確性。

圖8 Δu對系統響應的影響-有內力補償

最后，為了進一步驗證提出控制策略的正確性，仿真給定幅值為±1 mm、頻率為5 Hz的正弦信號時，此時采用不同的伺服閥零偏，并且使用自由度控制算法但無內力補償控制時系統的位移響應曲線和內力曲線如圖9所示。不同的伺服閥零偏使得系統的響應信號不同。系統的內力也隨不同的伺服閥零偏而不同，伺服閥零偏越大，內力越大，該現象與圖7現象類似。

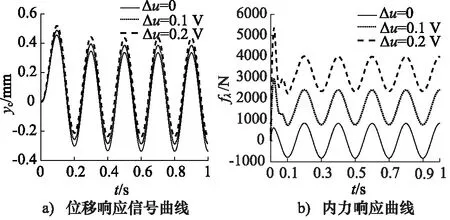
圖9 給定信號時Δu對內力的影響-無內力補償

圖10為給定幅值為±1 mm、頻率為5 Hz的正弦信號時，使用自由度控制算法，且加入內力補償控制時系統的位移響應曲線和內力曲線。盡管給定的電壓偏差信號不同。然而系統的位移響應信號迅速趨于相同。系統的內力也迅速衰減并趨于相同，說明提出的內力補償控制方法正確可行以保證電液雙缸系統的位置同步控制。

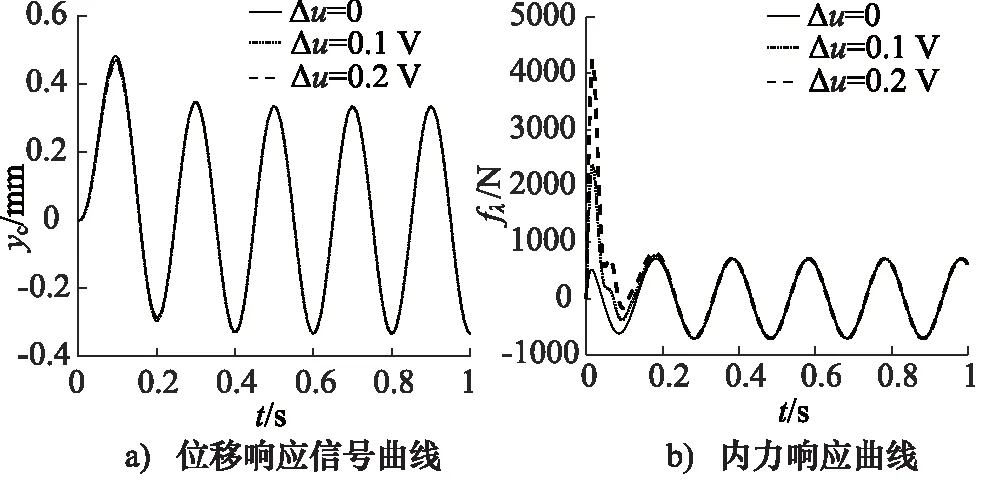
圖10 給定信號時Δu對內力的影響-有內力補償

3 結論

本研究建立了電液雙缸系統中位移測量誤差、機械安裝誤差、伺服閥零偏等因素對雙液壓缸同步誤差影響的數學模型，并分析了上述因素對系統內力的影響。針對該問題提出了基于自由度控制算法的同步控制策略并理論分析了該控制策略的正確性。最后，建立了電液雙缸同步控制系統仿真模型并進行了靜態和動態仿真驗證，仿真結果表明了理論分析的正確性和提出的基于自由度控制方法加入內力補償控制和位移補償控制后，電液雙缸系統的響應不受系統誤差的影響，兩液壓缸能夠同步穩定地跟蹤給定信號，提出的同步控制策略正確可行。