南京市仙林地區(qū)地下物流網(wǎng)絡(luò)節(jié)點(diǎn)建設(shè)模型

戚 佳

（浙江省杭州市蕭山區(qū)南陽街道辦事處，浙江 杭州 311200）

引言

交通擁堵是世界大城市都遇到的“困局”之一。導(dǎo)致城市交通擁堵的主要原因是交通需求激增所帶來的地面道路上車輛、車次數(shù)量巨增，其中部分是貨物物流的需求增長[1-2]。盡管貨車占城市機(jī)動(dòng)車總量的比例不大，但由于貨運(yùn)車輛一般體積較大、載重時(shí)行駛較慢，車流中如果混入重型車，會(huì)明顯降低道路的通行能力，因此，其占用城市道路資源的比例較大。因此，研究將貨運(yùn)車輛分離出來十分必要。

世界各國都在為解決城市交通和環(huán)境問題進(jìn)行積極探索，而處理好貨運(yùn)交通已成為共識(shí)。實(shí)踐證明[3]，僅通過增加地面交通設(shè)施來滿足不斷增長的交通需求，既不科學(xué)也不現(xiàn)實(shí)，地面道路不可能無限制地增加。因此“統(tǒng)籌規(guī)劃地上地下空間開發(fā)”勢在必行，“地下物流系統(tǒng)”正受到越來越多發(fā)達(dá)國家的重視。國外在此領(lǐng)域的先進(jìn)研究成果[4-6]包括德國研究的地下管道運(yùn)輸系統(tǒng)（Cargo Cap），日本設(shè)計(jì)的氣力囊體管道運(yùn)輸系統(tǒng)（PCP）和兩用卡車地下物流系統(tǒng)（DMT），美國提出的水力囊體管道運(yùn)輸系統(tǒng)（HCP）以及荷蘭研制的自動(dòng)導(dǎo)向車地下物流運(yùn)輸系統(tǒng)（AGV）技術(shù)等。文獻(xiàn)[7-8]表明，國內(nèi)在2002 年才開始出現(xiàn)地下物流網(wǎng)絡(luò)的研究，主要集中在地下物流網(wǎng)絡(luò)的概念、計(jì)算模型、選址優(yōu)化等方面的研究。而對于模型的實(shí)際開發(fā)和應(yīng)用研究非常少，尤其是針對特定城市情況下的地下物流網(wǎng)絡(luò)節(jié)點(diǎn)的確定。

本文以南京市仙林地區(qū)為例，以Toregas 集合覆蓋模型為基礎(chǔ)[9]，結(jié)合0-1 整數(shù)規(guī)劃模型，以節(jié)點(diǎn)數(shù)為目標(biāo)函數(shù)，以服務(wù)覆蓋范圍為約束條件[10]，采用Chvatal 算法求解，并借助LINGO 進(jìn)行計(jì)算。最終求得地下物流網(wǎng)絡(luò)的節(jié)點(diǎn)群，并與實(shí)際的OD 調(diào)查數(shù)據(jù)進(jìn)行比較，驗(yàn)證計(jì)算模型的合理性和準(zhǔn)確性。

1 Toregas 集合覆蓋模型

1.1 模型介紹

物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型應(yīng)用于集合覆蓋問題，目標(biāo)是確定建設(shè)最少的服務(wù)器來滿足每一個(gè)設(shè)備的需求。對于需求已知的區(qū)域點(diǎn)，設(shè)立相應(yīng)的目標(biāo)函數(shù)和約束條件，確定一組物流網(wǎng)絡(luò)節(jié)點(diǎn)來滿足這些區(qū)域點(diǎn)的需求量。它的數(shù)學(xué)模型是由Toregas 等人最早提出的，最初主要用于解決消防站和救護(hù)車等的應(yīng)急服務(wù)設(shè)施的選址問題上。它不僅能夠使用最少的物流節(jié)點(diǎn)滿足所有需區(qū)域點(diǎn)的需求，而且一定程度上能夠減少城市地下物流系統(tǒng)建設(shè)初期的投資費(fèi)用。物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型如圖1 所示。

基于Toregas 集合覆蓋模型，在19 和20 世紀(jì)，德國、日本、英國就已經(jīng)建成并運(yùn)行了用于運(yùn)送郵件的地下郵件運(yùn)輸系統(tǒng)[11-12]，釋放了地面的道路空間，減少了路面道路運(yùn)輸?shù)膲毫Γ岣吡宋锪鬟\(yùn)輸?shù)男蔥13]。德國和日本的地下運(yùn)輸網(wǎng)絡(luò)如圖2 所示。

1.2 建立物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型

假 設(shè) 所 有 二 級 節(jié) 點(diǎn) 的 集 合 為 S={e1，e2，...，en}，S1，S2，...，Sm是 S 的子集，若 J?{1，2...m}，且則稱 S={Sj}j?J為S 的一個(gè)集合覆蓋，意思是指S 中的每一個(gè)元素都至少含于S 的一個(gè)某一子集Sj（j?J）中，即被Sj覆蓋。目標(biāo)就是要尋找S 的一個(gè)基數(shù)最小的集合覆蓋，其中基數(shù)是集合中元素的個(gè)數(shù)。對于每一子集Sj（j=1，2，...，m），都引入相應(yīng)的決策變量。

其中目標(biāo)函數(shù)為滿足區(qū)域所有點(diǎn)需求的最少一級節(jié)點(diǎn)數(shù)，約束條件為每一個(gè)二級節(jié)點(diǎn)至少要被一個(gè)一級節(jié)點(diǎn)所覆蓋。

式中：xj為第j 個(gè)物流網(wǎng)絡(luò)節(jié)點(diǎn)；ej為第i 個(gè)區(qū)域需求點(diǎn)；j?J 為第j 個(gè)物流網(wǎng)絡(luò)節(jié)點(diǎn)能滿足Sj區(qū)域所有點(diǎn)的需求。

2 物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型求解

2.1 節(jié)點(diǎn)群數(shù)量求解

本文把物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型應(yīng)用于集合覆蓋問題，其目的在于運(yùn)用最少的一級節(jié)點(diǎn)數(shù)對城區(qū)內(nèi)所有的二級節(jié)點(diǎn)進(jìn)行覆蓋[14]。然而，集合覆蓋問題的求解比較困難，目前沒有一個(gè)精確的算法，因此，本文采用Chvatal 算法對其進(jìn)行近似求解。

步驟一：根據(jù)線性規(guī)劃的松弛性，將0-1 規(guī)劃的物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型的約束條件xj=0，1 改成xj≥0，這樣就得到0-1 規(guī)劃物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋的松弛模型。

步驟二：根據(jù)線性規(guī)劃的對偶性，將最小化問題模型轉(zhuǎn)成最大化問題模型

圖2 德國和日本的地下物流系統(tǒng)

步驟三：用Chvatal 法求近似解

根據(jù)南京市仙林區(qū)域的地圖，查詢了南京市仙林地區(qū)的物流供給分布點(diǎn)，初步得出該地區(qū)有46 個(gè)需求點(diǎn)，即 J=（e1，e2，...，e46） ，有 35 個(gè)供給點(diǎn)，即 x={x1，x2，...，x35}，然后建立0-1 線性規(guī)劃物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型的方程。

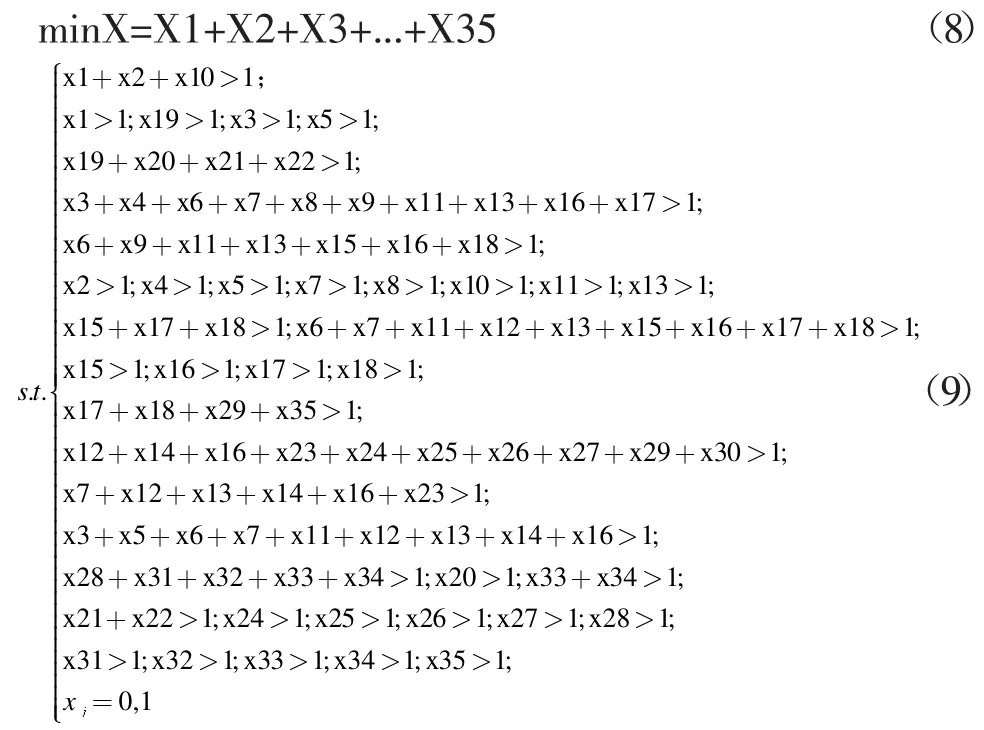
用LINGO 進(jìn)行求解一級物流網(wǎng)絡(luò)的節(jié)點(diǎn)個(gè)數(shù)，求解結(jié)果如圖3 所示：

圖3 LINGO 求解結(jié)果

從計(jì)算機(jī)求解的方程結(jié)果看，要完全覆蓋整個(gè)仙林地區(qū)的物流，至少需要27 個(gè)一級網(wǎng)絡(luò)節(jié)點(diǎn)，為了驗(yàn)證計(jì)算結(jié)果的準(zhǔn)確性，利用提供的OD 調(diào)查數(shù)據(jù)進(jìn)行了復(fù)核。

2.2 模型求解驗(yàn)證

仙林地區(qū)的區(qū)域劃分共有110 個(gè)區(qū)塊，根據(jù)OD 調(diào)查數(shù)據(jù)和節(jié)點(diǎn)劃分等級。對此OD 值介于0 和1 之間的，流量太小，可以忽略不計(jì)；OD 值介于1 和30 之間的，應(yīng)當(dāng)考慮建立二級物流網(wǎng)絡(luò)節(jié)點(diǎn)，并進(jìn)行服務(wù)覆蓋；OD 值大于30 的應(yīng)當(dāng)考慮建立一級物流網(wǎng)絡(luò)節(jié)點(diǎn)，并同時(shí)進(jìn)行服務(wù)覆蓋。又考慮到同樣的兩個(gè)地方由于起點(diǎn)和終點(diǎn)互換，它們的OD 數(shù)值就會(huì)不同，為此，統(tǒng)計(jì)出OD 數(shù)值大于30 的區(qū)域，并進(jìn)行綜合排名，最后一共有29 個(gè)區(qū)域適合建立一級物流網(wǎng)絡(luò)節(jié)點(diǎn)，其位置編號(hào)如表1 所示。

表1 一級節(jié)點(diǎn)位置統(tǒng)計(jì)

同樣，運(yùn)用OD 數(shù)值統(tǒng)計(jì)的方法，對二級物流網(wǎng)絡(luò)節(jié)點(diǎn)進(jìn)行統(tǒng)計(jì)分析，得出了二級物流網(wǎng)絡(luò)節(jié)點(diǎn)個(gè)數(shù)一共為35 個(gè)，然后，最后剩下來的所有區(qū)域一并將其劃為區(qū)域需求點(diǎn)，它們位置編號(hào)如表2 所示。

表2 二級物流網(wǎng)絡(luò)節(jié)點(diǎn)和剩余區(qū)域需求點(diǎn)位置統(tǒng)計(jì)

2.3 節(jié)點(diǎn)服務(wù)范圍

一級物流網(wǎng)絡(luò)節(jié)點(diǎn)，其功能相當(dāng)于城內(nèi)的物流集散中心，二級物流網(wǎng)絡(luò)節(jié)點(diǎn)才具有配送服務(wù)的功能[15-16]，根據(jù)運(yùn)輸載具的性能，二級物流網(wǎng)絡(luò)節(jié)點(diǎn)的平均服務(wù)半徑為3km。據(jù)此，畫出了二級物流節(jié)點(diǎn)的服務(wù)覆蓋范圍，其服務(wù)范圍如圖4 所示。

此外，為更加清晰地看到二級物流網(wǎng)絡(luò)節(jié)點(diǎn)的服務(wù)范圍內(nèi)的具體對象，根據(jù)求出的二級節(jié)點(diǎn)服務(wù)范圍圖，統(tǒng)計(jì)了各節(jié)點(diǎn)服務(wù)范圍內(nèi)的具體服務(wù)對象，其編號(hào)和數(shù)量如表3 所示。

表3 二級物流網(wǎng)絡(luò)節(jié)點(diǎn)服務(wù)覆蓋范圍內(nèi)具體服務(wù)對象統(tǒng)計(jì)

根據(jù)求出的一級節(jié)點(diǎn)群和OD 調(diào)查統(tǒng)計(jì)得出的二級節(jié)點(diǎn)群，按照二級節(jié)點(diǎn)不連接，貨物從一級節(jié)點(diǎn)群流向最近的二級節(jié)點(diǎn)群的原則，在地圖上將一級節(jié)點(diǎn)群和二級節(jié)點(diǎn)群進(jìn)行連接，結(jié)果見圖5。

3 結(jié)果分析

圖4 二級物流網(wǎng)絡(luò)節(jié)點(diǎn)的服務(wù)覆蓋范圍

圖5 一級和二級物流網(wǎng)絡(luò)節(jié)點(diǎn)連接

對于物流網(wǎng)絡(luò)節(jié)點(diǎn)選擇，本文創(chuàng)新性地結(jié)合0-1 整數(shù)規(guī)劃模型和Chvatal 算法，建立0-1 規(guī)劃物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型，并通過LINGO 進(jìn)行求解，由圖3 可以看出，求解的結(jié)果顯示至少需要27 個(gè)一級節(jié)點(diǎn)才能覆蓋整個(gè)仙林地區(qū)。但根據(jù)OD 調(diào)查數(shù)據(jù)進(jìn)行統(tǒng)計(jì)分析，得出需要29個(gè)一級節(jié)點(diǎn)才能覆蓋整個(gè)仙林地區(qū)，兩個(gè)結(jié)果誤差較小，說明模型計(jì)算的結(jié)果較好，但最終選擇建立29 個(gè)一級節(jié)點(diǎn)。

對于服務(wù)范圍，在二級節(jié)點(diǎn)上進(jìn)行劃分，按照平均覆蓋服務(wù)半徑為3 公里。由圖4 可以看出，在仙林地區(qū)左下部，覆蓋比較密集，這也比較符合該地區(qū)人口和建筑區(qū)域密集的特點(diǎn)，而在右上部，建筑和人口很稀疏，劃分的服務(wù)區(qū)域并沒有完全覆蓋整個(gè)地圖。總體而言，29 個(gè)一級節(jié)點(diǎn)，36 個(gè)二級節(jié)點(diǎn)，服務(wù)范圍能較好地覆蓋整個(gè)地區(qū)。

此外，由圖5 的網(wǎng)絡(luò)連接情況可以發(fā)現(xiàn)，一級網(wǎng)絡(luò)節(jié)點(diǎn)和二級網(wǎng)絡(luò)節(jié)點(diǎn)能較好地與建筑密集度相匹配，一級節(jié)點(diǎn)和二級節(jié)點(diǎn)的分布基本包含沿線所有的服務(wù)點(diǎn)，這表明該地下物流網(wǎng)絡(luò)運(yùn)載能力基本能達(dá)到服務(wù)整個(gè)地區(qū)的需求。

4 結(jié)論

本文采用0-1 整數(shù)規(guī)劃模型和Chvatal 算法建立地下物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型，并使用計(jì)算機(jī)進(jìn)行模擬求解。取得了如下結(jié)果：

（1）參考Toregas 集合覆蓋模型，介紹了地下物流網(wǎng)絡(luò)節(jié)點(diǎn)模型建立和求解的過程，并根據(jù)地下物流網(wǎng)絡(luò)節(jié)點(diǎn)的特征，結(jié)合了0-1 整數(shù)規(guī)劃和Chvatal 算法，并借助計(jì)算機(jī)進(jìn)行求解。

（2）結(jié)合 0-1 整數(shù)規(guī)劃模型和Chvatal 算法的物流網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋模型，其求解結(jié)果與實(shí)際的網(wǎng)絡(luò)節(jié)點(diǎn)需求量較為接近。表明模擬求解的結(jié)果較好，可以作為地下物流網(wǎng)絡(luò)節(jié)點(diǎn)設(shè)計(jì)的初步方案。

（3）整個(gè)南京仙林地區(qū)的地下物流網(wǎng)絡(luò)需要29 個(gè)一級節(jié)點(diǎn)，36 個(gè)二級節(jié)點(diǎn)，服務(wù)范圍即可覆蓋整個(gè)區(qū)域。并且，節(jié)點(diǎn)覆蓋密度與地圖上建筑和人口分布的趨勢一致。因此，該地下物流網(wǎng)絡(luò)節(jié)點(diǎn)群能較好地滿足當(dāng)前的物流需求。