基于網絡結構與內容分布的新媒體事件聚類研究

馬昊 馬曉悅

摘?要：[目的/意義]現有新媒體事件的聚類研究聚焦于事件的單一維度屬性，并未考慮事件傳播的網絡結構特征和文本分布特征。[方法/過程]本研究基于信息熵的相關概念，提出基于網絡結構熵與內容分布熵的事件聚類模型。模型在表征事件網絡結構特征、內容分布特征的基礎上完成跨內容事件相似度對比，并使用圖表示學習算法與k-means聚類算法對事件進行分析與聚類。本文選取113例微博事件作為實驗對象，并使用事件基本屬性（點贊、評論、轉發等）作為聚類對照實驗組。[結論/發現]實驗結果分析表明，本研究提出的模型能夠捕捉到新媒體事件更深層次的傳播、分布特征，能夠對現有相似度計算指標進行完善與補充。[創新/價值]本研究不僅能夠從多維度層次提取事件的傳播特征，即事件網絡結構特征和內容分布特征，還能夠為輿情預測、管控提供支持，通過熵維度的信息變化監測不同事件之間的傳播共性，輔助后續輿情事件的預測與監管。

關鍵詞：網絡結構;內容分布;新媒體事件;微博傳播;網絡結構熵;信息分布熵;事件聚類;圖表示學習

DOI：10.3969/j.issn.1008-0821.2021.02.004

〔中圖分類號〕G206?〔文獻標識碼〕A?〔文章編號〕1008-0821（2021）02-0030-12

Abstract：[Purpose/Significance]The existing clustering research of new media events focuses on the single-dimensional attributes of events，and does not consider the network structure characteristics and text distribution characteristics of event propagation.[Method/Process]This research was inspired by the concept of information entropy，and proposed an event clustering model based on network structure entropy and content distribution entropy.The model completed cross-content event similarity comparison on the basis of characterizing event network structure characteristics and content distribution characteristics，then Network Representation Learning algorithm and k-means clustering algorithm cluster the events.This paper selected 113 microblog events as the experimental objects，and used the basic attributes of the events（likes，comments，reposts，etc.）as the cluster control experimental group.[Results/Conclusion]The analysis of the experimental results showed that the model proposed in this study could capture the deeper communication and distribution characteristics of new media events.At the same time，it could improve and supplement existing similarity calculation indicators.[Originality/Value]This research can not only extract the propagation characteristics of the event from multi-dimensional levels，that is，the characteristics of the event network structure and the distribution of event content.Also it can provide support for public opinion prediction and control.The model can also monitor the communication commonality between different events through the entropy dimension of information changes to assist subsequent reflection on public opinion events.

Key words：network structure entropy;information distribution entropy;event clustering;network representation learning;network structure;content distribution;new media events;microblog;communication

信息技術和自媒體行業的飛速發展使得互聯網行業中用戶創造內容的數量呈現指數級增長[1]。在海量用戶生產數據的背景下，信息的自動聚類與分類成為研究焦點[2-3]。具體到新媒體環境中，由用戶生成信息所構成的新媒體事件聚類與分類是新媒體輿情管理與檢測的一項重點研究[4-5]。如何精確地度量事件之間的相似度、對事件進行聚類分析和分類成為組織和使用輿情信息的先決條件與研究熱點。

現有聚類研究局限于新媒體事件的文本內容，導致相關計算指標存在一定的局限性。學術界目前對于事件聚類亦或表征事件的文本聚類多關注于信息的特征提取，如早期的詞袋模型[6]及后續對詞語進行加權的TF-IDF模型[7-8]，并針對研究內容展開了多個領域的探索，如網絡短文本聚類[9]、新聞文本聚類[10]等。而新媒體事件是以新媒體為載體的網絡熱點事件，具有兩大特征：雙向傳遞與用戶創造內容。雙向傳遞即意味著用戶既可作為信息的接收者亦可成為信息的生產者;用戶創造內容則指事件中傳遞的信息大多由用戶創造[11]。而這種傳播特點的深層邏輯是用戶對于某一話題的支持與關注。之前的研究也表明，用戶在新媒體事件傳播中形成的傳播網絡及網絡中的文本代表著用戶的喜好、影響力[12]、事件觀點等屬性[13]。這使得用戶創造內容與用戶在事件之間形成的傳播網絡成為新媒體事件傳播的重要構成部分[14]。且現有方法并未將事件的網絡結構與事件的內容分布結合考慮，現存指標也并未對跨領域、跨內容事件的相似度進行計算。

基于此，本文提出綜合考慮網絡結構與內容分布的信息熵相似度度量模型，用于新媒體事件的類別計算。模型能夠從事件傳播的網絡結構和內容分布對事件特征進行提取，同時基于熵的概念構建相似度計算指標以完成跨事件對比。最后本文使用基于NRL（Network Representation Learning，圖表示學習）和k-means的聚類方法將傳統指標與本文構建指標在事件聚類層面的差異進行對比，結果證明，本文指標能夠考慮事件在傳播過程中網絡結構和文本分布等深層特征，完善和補充傳統指標對相似度的計算和聚類的劃分。

1?相關研究

本研究模型旨在對新媒體事件的網絡結構特征及文本分布特征進行量化表征。基于本文模型結構，目前國內外關于新媒體事件相似度計算、事件聚類的相關研究可分為兩大類別：一是基于圖論或者復雜網絡的網絡結構相似度研究;二是基于新媒體短文本內容的內容特征相似度研究。

1.1?新媒體環境中事件網絡特征相似度研究

新媒體環境中網絡結構相似度研究根據其最終的研究對象分為兩類。首先是網絡中節點的相似性研究，其次是網絡整體結構相似性研究。

網絡節點相似性研究主要將用戶等研究對象作為社交網絡節點，研究其在網絡中的相似度。Celik M等在其研究中提出了一種根據用戶在新媒體社交中訪問站點的社交重要性來對用戶間相似性進行量化的方法。該方法使用用戶經常訪問具有重要社交價值的站點對用戶進行網絡特征表示，使用編輯距離（Levenshtein距離）實現用戶之間相似度的量化[15]。Zhou X等提出了FRUI-P模型以識別跨平臺匿名用戶。將社交網絡中各用戶的朋友特征提取至朋友特征向量中。最后，開發了一對一的映射方案，以基于相似性來識別用戶[16]。

網絡整體相似性研究是將新媒體事件傳播網絡看作整體，度量網絡整體相似性以達成相應的研究目標。Jiang L等構造了一種將醫療保健社交媒體數據表示為異構醫療保健信息網絡的方法。該方法從局部（直接連接）和全局（間接連接）結構出發度量網絡相似性，以此實現相似醫療保健用戶發現和推薦。其研究結果表明，基于結構的相似性方法相較于基于內容的方法在準確度與效率方面具有更好的性能[17]。此外，Li Y等基于不同社交網絡中友誼網絡的相似性，提出了跨網絡的用戶識別與發現方法[18]。田世海等使用事件間共現作為新媒體事件之間的關系鏈接構建輿情事件復雜網絡，以此計算事件相似度并完成輿情事件的聚類分析[19]。

1.2?新媒體環境中事件內容特征相似度研究

新媒體環境中內容相似度研究主要針對短文本內容的相似度，根據研究方法可分為兩類，首先是基于單詞的短文本相似度計算方法，其次是基于語義的短文本相似度計算方法。

基于單詞的短文本相似度計算將單詞作為最小分析單位，對應的將短文本視為單詞的組合。因此在這類方法中，短文本的相似度即為組成該短文本的單詞對相似度。此類方法又可分為基于知識的相似度計算和基于語料的相似度計算。基于知識的相似度計算依賴于人工認知對詞組間關系的標記。其中典型案例為WordNet[20]，一種基于認知語言學組成的語義網絡。Lee J C等將單詞在WordNet中的最短路徑長度作為相似度計算指標[21]。也有學者將詞嵌入模型與WordNet模型相結合以構建新的相似度計算方法[22]。基于預料的相似度則將單詞嵌入具體的預料之中，根據單詞在當前預料中的分布特征對單詞間相似度進行計算。其中最具代表性的方法是詞移動距離[23]。即在當前語料組成的空間中，一個單詞從其位置移動到另一個單詞所在位置之間的距離作為其詞移動距離，以對單詞間相似度進行表征。

基于語義的短文本相似度計算將文本中詞語分布的真實含義考慮在內。其中最為經典的方法為LSA系列模型[24]。模型假設單詞語義及其理解可從其在語料中的分布得出，即具有相似上下文的詞語具有相同的語義。在此基礎上，Hofmann T提出了基于LSA的概率潛在語義分析模型（PLSA），從概率視角對文本建模[25]。Blei D M等則提出了潛在的狄利克雷分布（LDA），為PLSA添加了貝葉斯框架，并使用單詞和文本之間的概率分布來表達文本含義[26]。也有研究人員試圖將短文本編碼為機器與用戶易為理解的形式，并在此基礎上進行相似度計算。ESA（Explicit Semantic Analysis）模型是其中的經典模型。Gabrilovich E等將維基百科作為文本的概念空間，將短文本表示為帶有權重的維基百科空間向量，后續的相似度計算則回歸為空間向量相似度計算[27]。

1.3?現存問題及研究目標

新媒體事件的相關聚類研究較少，且研究內容多局限于特定的指標與屬性，并未從新媒體事件的傳播內容特征及其傳播網絡特征視角出發進行綜合探究。傳統的事件相似度度量手段無法準確地表征新媒體事件的多維度特征，且缺少跨內容領域的相似度指標。

本研究創新點如下：首先，從網絡結構維度與內容分布維度出發捕捉新媒體事件特征。具體來說，本研究從復雜網絡角度出發，根據網絡結構熵的概念構建了新媒體事件在傳播網絡的特征屬性。從新媒體事件內容相似度出發，基于傳播網絡對新媒體事件文本內容分布網絡進行重構，并延續網絡結構熵的概念構建了內容分布熵以表征新媒體事件內容特征屬性。

其次，本研究從熵的角度出發，將事件相似度對比映射至熵維度，在保留事件內容分布屬性的基礎上，實現了跨內容領域的不同事件相似度對比。研究將事件特征分為網絡結構與文本分布兩大維度，二者從局部細粒度和整體粗粒度表征事件特征。具體而言，局部細粒度將網絡結構與文本分布視為概率分布，求取局部屬性對全局屬性的代表性，以此來表征事件內容的混亂程度，即熵;全局粗粒度則是對局部細粒度的補充，將事件規模屬性納入研究范圍。由于熵自身特征及其對文本分布的網絡重構，本研究能夠將不同領域事件映射至熵維度進行對比。

最后，根據本研究提出的相似度計算方法，使用NRL（Network Representation Learning，圖表示學習）和k-means算法對事件進行聚類分析，并使用事件基礎屬性設置對照組進行對比。

2?基于網絡與內容結構熵的事件相似度度量模型

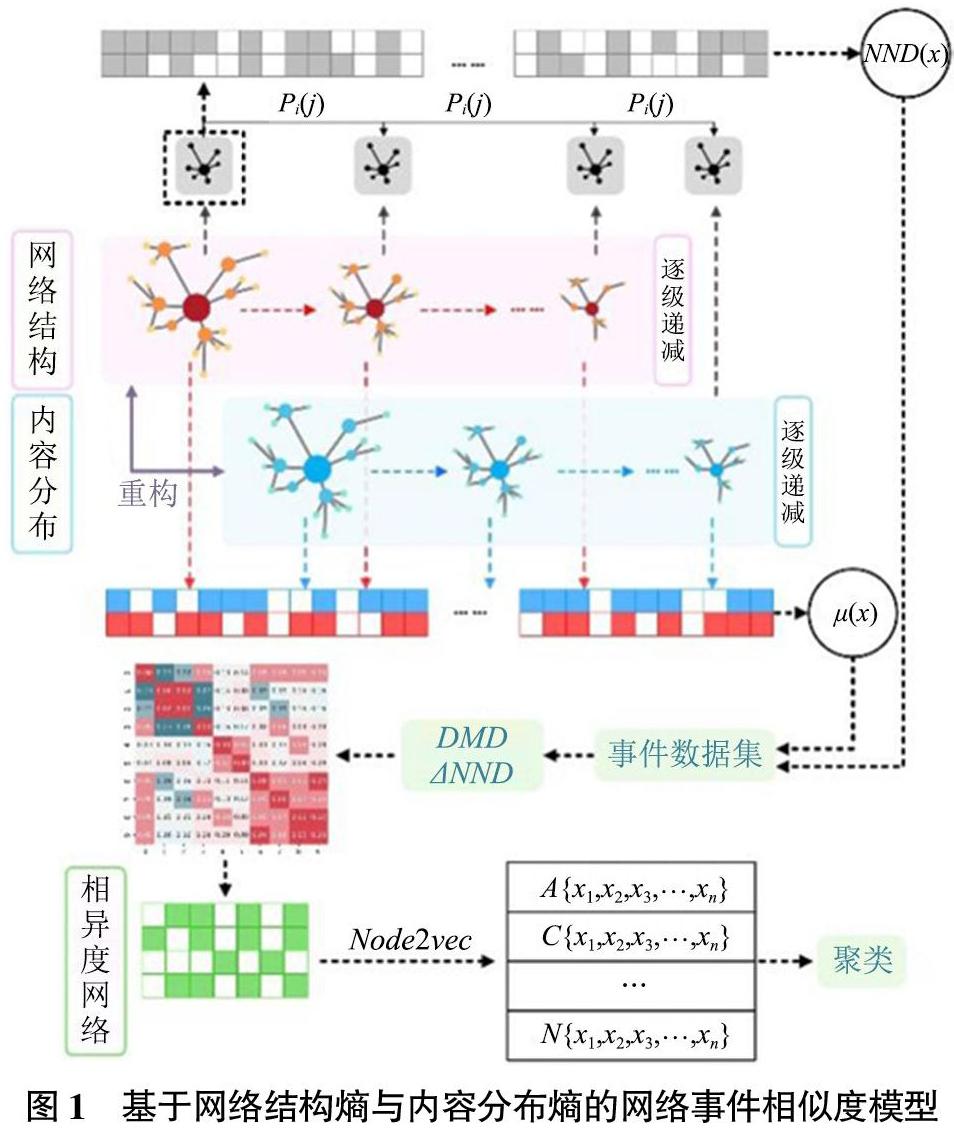
本模型旨在將新媒體環境中內容數據與聯系數據抽象為多維度復雜網絡，并使用基于復雜網絡結構熵、基于內容分布結構熵的模型對其進行相似度計算，模型組成與流程示意如圖1所示。

從事件內容數據與聯系數據的特征維度出發，模型可分為兩部分：基于網絡結構熵的相似度度量和基于內容分布熵的相似度度量。前者度量新媒體環境下事件傳播形成的網絡拓撲結構相似度，后者度量新媒體環境下事件傳播中內容變化（即內容熵）的相似度。

基于網絡結構熵的相似度可從網絡結構自身的復雜度（NND，Network Node Dispersion，網絡節點離散度）及兩個網絡之間的結構相似度（EMD，Earth Mover's Distance，陸地移動距離，也叫第一Wasserstein距離）對網絡拓撲結構相似性進行量化表征;基于內容分布的結構熵與之類似，本文使用Bert模型基于內容相似度對事件傳播網絡進行重構——生成“內容分布網絡”，并在該網絡上度量NND與EMD指標。

本文提出的模型能夠從網絡結構與內容分布結構兩個維度，研究對象自身復雜度與對象之間相似度兩個指標對于新媒體網絡事件進行相似度計算。

在實例驗證階段，本文對采集的微博事件進行相似度度量后形成事件距離矩陣，其次對其進行基于圖表示學習聚類分析，使用事件原有屬性作為聚類對照組。結果表明，本模型能夠從內容數據與網絡聯系兩個層面對事件的特征進行捕捉，能夠對傳統事件相似度度量方法指標進行補充與完善。

2.1?基于熵的相似度度量

新媒體網絡事件在傳播過程中體現出“多個重要傳播節點引導，大量普通節點依附參與討論，其隨時間節點的討論規模遞減”的狀態，如圖2所示。

圖2?新媒體事件的傳播演變

以新浪微博為例，特定事件相關微博通常以“#事件關鍵詞#”形式的超鏈接為索引。在事件傳播過程中，少數節點引導著多數普通用戶節點進行討論與交互，且隨著時間演變討論與交互的規模逐漸減小。

模型旨在度量此類網絡結構分布的內在復雜度及網絡與其他網絡間分布的相似度，從而在保留網絡拓撲結構的前提下完成事件間的距離計算;同理，借助自然語言處理模型對事件傳播網絡進行重構得到內容分布網絡后，模型能夠計算事件內容分布的內在復雜度、內容與其他事件內容分布之間的相似度，從而保證了跨事件內容相似度計算的可能性，并保留了網絡的拓撲結構。

2.1.1?基于網絡結構熵的相似度

模型的基礎理念事件傳播網絡理解為基于節點度的概率分布。為清晰地介紹本文模型，引入基本概念KL散度，如式（1）所示：

其中，p和q表示兩種維度為N的概率分布。

KL散度又稱為相對熵，是一種度量兩種分布相似度的方法。以該理論為基礎，學者Schieber T等提出了網絡相似度模型，其中NND（Network Node Dispersion，網絡節點離散度）子模塊將網絡中節點的度看作概率分布以表征其結構熵，其研究證明該方法能夠很好地在拓撲結構層面度量網絡相似度且具有較低的計算要求[28]。

本文受該模型啟發，綜合考慮網絡規模與網絡拓撲結構相似性，定義基于結構熵的網絡相似度，如式（2）所示：

其中，g1和g2為待計算相似度的網絡，EMD為陸地移動距離也稱Wasserstein距離[29]，NND為網絡節點離散度指標，w1與w2為權重系數默認取值0.5，μg1={μ1，μ1，…，μN}w。

NND指標的詳細定義如式（3）所示：

其中，J（P1，P2，…，PN）表示JS距離，詳細定義如式（4）。節點Pi的節點度概率分布可表示為Pi={Pi（j）}，Pi（j）表示對于節點i來說與其距離為j的節點的比例。d為當前網絡直徑，目的是對計算結果進行標準化。

其中，N表示當前網絡中節點的總數量，μj定義如式（5）所示：

其中，Pi（j）定義與上式相同，N表示當前網絡中節點的總數量。

因此，NND模塊能夠很好地捕捉網絡的拓撲結構的熵值，即網絡平均局部節點度分布的概率對總體網絡節點分布概率的表征度。但其對于k-regular網絡不能進行區分[28]，對于k-regular網絡而言，局部節點度分布概率完全等同于全局節點分布概率，Schieber T在其研究中對該方法進行詳實的改進和說明。

在網絡事件中，僅使用NND指標，模型可能對過度傳播的熱門事件和傳播結構單一的冷門事件缺乏區分度，因為這些事件的局部節點均能夠很好地表征全體節點的度分布概率。因此，本文對NND模型進行改進，使用EMD距離作為NND的補充，如式（2）。EMD距離能夠度量將兩個分布移動為相同分布所花費的最小距離。μg1={μ1，μ1，…，μN}作為EMD的輸入能夠將網絡結構的規模納入度量中，彌補了NND的缺陷。

本文旨在構建跨領域、跨事件類型的相似度度量方法，這種將網絡特征抽象為熵的方法能夠有效實現跨類型計算。

2.1.2?基于內容分布熵的相似度

基于結構熵的相似度度量從事件網絡拓撲結構度量了事件的相似性，即單個節點的度概率分布在多大程度上可表征網絡整體，同時加以事件規模參數（EMD）對其進行修正。

內容分布熵的相似度計算與基于網絡結構熵的相似度計算所使用的基本方法相同，但前者的相似度計算基于重構后的內容相似網絡，后者的相似度計算基于事件傳播過程中的真實聯系網絡。

重構內容相似度網絡的方法如下：①使用BERT模型作為短文本相似度計算指標;②根據事件傳播網絡結構，計算節點之間文本相似度;③使用相似度均值作為判斷不同節點之間是否存在新連接的閾值;④根據閾值重構文本分布網絡。

最終，基于熵的網絡相似度模型如式（6）：

其中，Dt（g1，g2）、Dn（g1，g2）分別表示基于內容分布熵的相似度與基于網絡結構熵的相似度，w1與w2為權重系數默認取值0.5。

2.2?基于NRL和k-means的事件聚類模型

本文相似度計算模型可直接得出事件之間的距離或多個事件間的距離矩陣。為進一步論證本文模型的有效性和本文模型與傳統事件相似性計算方法的不同之處，本文選擇對事件距離矩陣進行基于NRL（圖表示學習）和k-means的聚類分析，并將事件基本屬性特征組作為聚類對照組進行分析。選擇的事件基本屬性如式（8）。

其中，Ei表示網絡事件i，Mi、Ii分別表示其對應的媒介數量向量，即包含圖片與視頻數量;事件影響力向量，其中包括評論用戶數量、轉發用戶數量、點贊用戶數量。上述向量均進行標準化。

NRL是一種將圖類型數據進行降維并保留其圖形結構特征屬性的有效方法，本文選擇Node2Vec算法[30]對事件距離舉證進行向量化，使用k-means算法對事件向量進行聚類。對照組基于事件基本屬性特征直接進行k-means聚類分析。

3?模型實例分析

本文隨機選擇了113例微博網絡事件。事件由“#”加事件關鍵詞的超鏈接進行索引，所有包含該鏈接的事件被微博平臺定義為話題，并提供單獨頁面供用戶瀏覽。所收集事件的微博討論量均在10w左右，事件涉及領域及其規模各不相同。

3.1?事件概述

根據模型對數據的需求，采集數據屬性包括事件名稱、事件分布內容、發布內容點贊數、發表內容評論數、發布內容轉發數（三者即式（8）中的事件影響力向量，表1中的數據為三者均值和）。

計算事件內各個博文的平均媒介數量、平均影響力、平均原創內容量并對其進行描述性統計，結果如表1、表2所示。

事件平均可視化媒介數量穩定在1.09/條微博左右，標準差為0.08;事件平均影響力則因為事件的領域和關注人群不同呈現出較大差異，標準差為55 680.71;事件平均原創內容量是對原創博文長度的度量。受微博平臺博文數量限制，事件平均原創量均值為102.58，標準差為3.47。

3.2?基于熵的相似度度量結果

數據集中各個事件的網絡結構熵與事件內容熵（即NND指標）如圖3所示。

圖中橫坐標為事件編號，縱坐標為標準化后的NND值。在不同事件中，相比于事件網絡結構重構后的事件內容分布網絡普遍具有更高的NND值。重構后的事件分布網絡具有更高混亂度，即局部信息分布難以表征全體信息分布情況。

EMD彌補了NND對網絡規模不敏感的缺點，從網絡總體基于度的概率分布對兩個網絡進行距離計算。圖4為部分事件EMD距離熱力圖，橫縱坐標為事件編號，圖中顏色的填充變化對應橫縱坐標下的具體數值即事件之間的EMD距離。距離數值高說明事件之間相似度小，事件網絡的度分布差異度較大，對應填充顏色為藍色;距離數值低說明事件之間相似度大，事件網絡的度分布差異度較小，對應填充顏色為紅色（紅色與藍色的深淺變化由繪圖算法基于當前數據的分布給出，即規定極小值為紅色、極大值為藍色，其余顏色深淺變化由其具體數值與極值之間的差值決定，差值越高顏色越淺），詳細標度見圖右側圖例。由圖可知網絡結構EMD與文本分布（內容分布）EMD總體具有一致性，但在個別事件中存在較大差異。

不同維度EMD與NND值加權求和后形成最終事件距離指標，圖5為部分事件距離熱力圖，其中橫縱坐標為事件編號。圖中顏色的填充變化對應橫縱坐標下的具體數值即事件之間的相異度，相異度數值高說明事件之間相似度小，對應填充顏色為藍色;相異度數值低說明事件之間相似度大，對應填充顏色為紅色（紅色與藍色的深淺變化由繪圖算法基于當前數據的分布給出，即規定極小值為紅色、極大值為藍色，其余顏色深淺變化由其具體數值與極值之間的差值決定，差值越高顏色越淺），詳細標度見圖右側圖例。左側子圖為最終事件距離矩陣，中間子圖為基于網絡結構的事件距離矩陣，右側子圖為基于重構文本分布網絡的事件距離矩陣。由圖可知，基于網絡結構和基于文本分布網絡均能捕捉到事件的相似特征，且二者總體具有一致性。體現在圖中為二者熱度圖矩陣色塊分布整體較為一致，局部存在不同。二者加權融合為最終的事件距離矩陣——事件相異度矩陣。

3.3?事件聚類結果

使用Grover A等提供的Node2Vec方法對事件距離矩陣進行向量化[30]。最終將事件的聚類分析分為實驗組與對照組。實驗組使用事件相異度矩陣作為輸入，通過Node2vec表示為事件特征向量，最終通過k-means進行聚類分析;對照組使用事件基本特征作為輸入向量，其定義見式（8），最終使用k-means進行聚類分析。

1）實驗組聚類結果

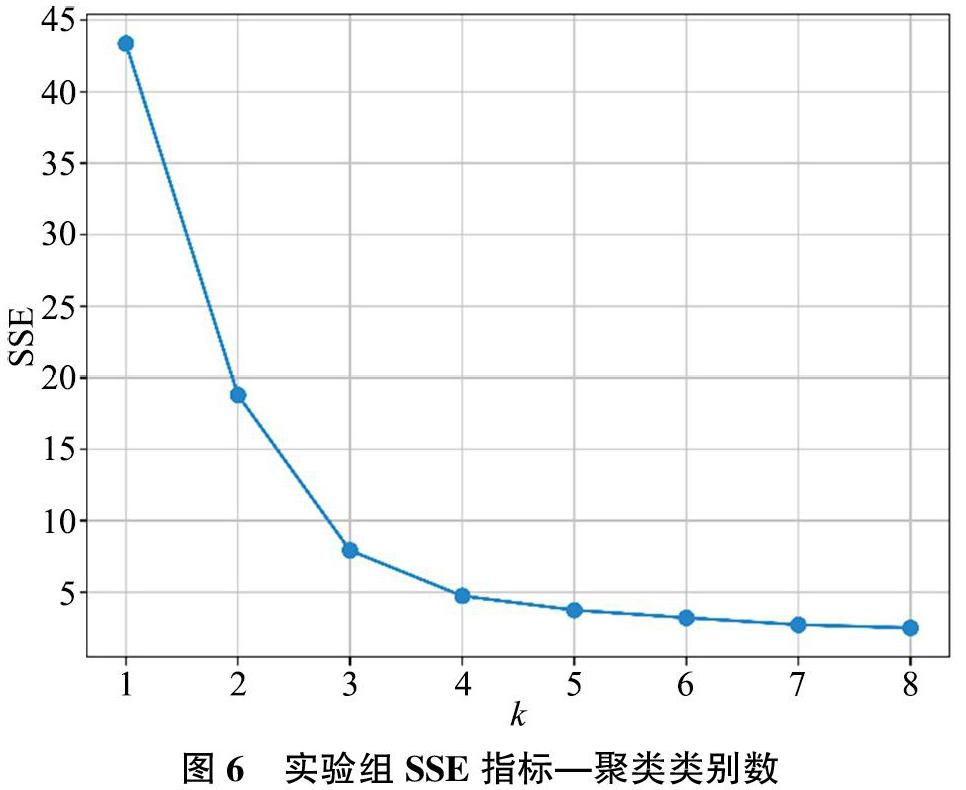
使用SSE（Sum of the Squared Errors，誤差平方和）繪制聚類“肘部圖”獲得的最佳聚類類別數如圖6所示。

在k=4時，SSE指標迅速減小，此時k對應較為真實的聚類類別數。對于聚類數據進行降維繪圖[31]，得到其最終類別分布結果如圖7所示。

由圖7可知，類別-2具有最多的樣本數（N=66），類別-4次之（N=35），類別-1樣本數N=10，類別-3樣本數量最小（N=2）。通過觀察原始數據，最終聚類結果中各個類別典型事件與特征如表3所示。

表中NND值為該類中NND均值標準化后的數值。由表可知，類別-1中事件傳播結構均勻，即局部節點能夠很好地表征整體節點，但其文本分布復雜，即局部文本不能較好地表征全體;類別-2中事件數量最多，其傳播結構均勻、文本分布復雜，但程度均低于類別-1;類別-3中事件網絡結構NND和文本分布NND較小，說明局部信息能夠很好地表征整體，具體到實際數據中為突發危機事件;類別-4中不論是網絡結構還是文本分布，局部信息都不能很好地表征全體，事件引發較多爭議和討論，傳播網絡結構不規則。

2）對照組聚類結果

對于對照組同樣使用SSE指標尋找最優聚類類別數，結果如圖8所示。

在k=4時，SSE指標迅速減小，此時k對應較為真實的聚類類別數。同樣，對于聚類數據進行降維繪圖，得到對照組最終類別分布結果如圖9所示。

對照組聚類結果中：類別-1事件在討論人規模與圖片視頻等媒介數量最多;類別-2中事件參與討論人數較多，但圖片視頻等媒介數量較少;類別-3中事件參與討論人數較多，圖片視頻等媒介數量較多;類別-4事件參與人數較少，圖片媒介數量較多。

實驗組（熵聚類）與對照組（特征聚類）事件分類的關系如圖10所示。

圖中熵聚類，即本實驗提出的方法能夠對傳統的類別劃分進行補充。傳統的數據基礎特征僅針對事件淺層數據特征的變化將事件進行分組，且組間數據差異大（86∶21∶4∶2），不能很好地區分事件;依據本文提出的模型熵聚類考慮了事件規模、網絡結構、文本分布等特征，能夠對事件特征進行精細捕捉，從而完成跨領域但不舍棄內容的相似度度量與聚類分析。

4?討?論

4.1?模型可捕捉新媒體事件傳播中的“結構簇”與“內容簇”的分布特征

新媒體事件相似度計算、聚類與分類的研究實質是對新媒體環境中同質性內容與異質性內容進行分化，即同類事件間相似度最大且非同類事件間相似度最小。熵在信息中的本質是度量系統的“內在的混亂程度”，因此新媒體事件聚類是尋求事件分類后熵的最小化。本研究將新媒體事件中相似的網絡結構與相似的內容分布作為局部的“結構簇”與“內容簇”，“結構簇”基于用戶評論行為形成的局部網絡，“內容簇”是基于用戶分布文本相似度形成的重構網絡。本研究提出NND指標對“簇”的分布特征進行量化，即量化新媒體事件的熵。在本次實驗中，基于熵的相似度度量模型能夠從網絡事件網絡結構維度和事件內容分布維度出發，考慮事件內部分布不一致性和事件規模兩個因素，最終形成了事件相似度度量的綜合指標。體現在以下3個方面。

首先，模型能夠提取事件傳播中“網絡結構簇”的分布特征。受Schieber T等提出的NND概念的啟發[28]，本文將網絡結構看作基于度的概率分布，NND能夠度量在網絡中單個節點對于整體數據的表征程度，如式（2）。在新媒體事件中，基于用戶評論等信息行為，事件的傳播網絡自發形成“結構簇”。“結構簇”的數量及其大小因不同事件而相異，但其分布是否一致具有可量化性。若事件“結構簇”分布較為均勻則NND數值較小，若事件“結構簇”分布具有較大差異，即事件“結構簇”分布對于事件整體傳播網絡的表征性較弱，事件“結構簇”分布較為不均勻，NND數值較高。

其次，模型能夠提取事件傳播中“內容分布簇”的分布特征。與網絡結構相異，網絡事件中并不存在明確的文本網絡結構且各事件描述對象與內容均不相同，文本間不存在明確的上下文關系，因此導致文本分布網絡不能直接對比，文本網絡不能直接沿用傳播的網絡結構。本文使用基于Bert的短文本相似度度量方法對文本網絡進行重構。重構后的網絡根據用戶發布文本之間的相似度對內容分布進行“簇”劃分，每個文本都有其歸屬的“內容分布簇”，因此重構后的文本分布能夠直接使用NND作為度量其一致性的手段。

最后，模型能夠提取事件網絡結構規模和文本分布規模作為補充。由于NND本質上是對目標內部一致性的度量，即“簇”與整體網絡之間的表征程度，因此在網絡結構相似或者文本分布相似但規模差距巨大的事件無法被區分，而事件規模是網絡事件進行區分的一項不可忽視的指標，因此研究選取EMD距離作為NND指標的補充，使模型在跨事件的同時兼顧事件規模。

4.2?模型揭示了異質新媒體事件傳播的普遍規律

本研究從“熵”的角度出發，以不同維度事件“簇”分布對于事件總體的表征性對事件之間的相似度進行度量并完成了聚類。由于是局部“簇”與總體網絡間的對比，即熵的對比，因此本研究模型天然具有跨事件性，即可將異質性新媒體事件映射到熵維度直接進行對比，而忽略其文本、網絡的具體差異，從而發現異質性新媒體事件間的普遍規律。

首先，相較于內容分布，事件網絡結構更容易形成穩定均勻的“結構簇”，即相較于內容分布維度中局部與全局的表征性關系，新媒體事件局部網絡結構更能夠表征全局網絡結構，如圖2所示。相較于內容分布，新媒體事件在網絡結構維度具有更低的NND數值。數據角度，事件傳播的網絡局部特征能夠更好地表征整體網絡，網絡結構較為均勻，網絡中“結構簇”的規模較為相近。事件與用戶交互角度，用戶在新媒體事件的評論過程中形成“結構簇”與“內容簇”，“結構簇”分布較之“內容簇”分布規模更為均勻。說明在新媒體事件中，用戶討論內容難以形成規模一致的“內容簇”，即難以達成普遍的意見統一。

其次，“結構簇”對于新媒體事件具有更好的區分度。如表3內容所示，本研究將新媒體事件聚為4類，其中類別1特征為：“結構簇”相對均勻，“內容簇”差異較大;類別2特征為：“結構簇”差異較大，“內容簇”差異較大;類別3特征為：“結構簇”均勻，“內容簇”差異較小;類別4特征為：“結構簇”差異較大，“內容簇”差異較大。結合不同類別中對應的具體事件可得出如下結論，當事件為極富爭議性時，“結構簇”差異巨大，如類別4;當事件易在新媒體環境中達成一致、缺少爭議時，“結構簇”分布均勻差異較小，如類別3突發危機事件。

4.3?基于熵的相似度度量模型是對傳統模型的補充和擴展

本文提出的相似度度量模型并非是對現有相似度度量指標的否定和取代，而是對現有指標、方法的補充與完善。具體體現在以下兩個方面：

一方面，模型從熵的角度——目標局部特征從全局的表征性來對事件傳播的網絡結構進行相似度計算。這種方法天然具有可比性，即目標對象局部與全局的表征關系無量綱，模型可以對于不同領域事件、不同規模事件進行相似度對比。這是對傳統方法局限于特定領域無法進行跨事件對比的補充。同時，網絡結構NND度量了事件網絡結構的變化。事件傳播網絡結構的變化暗示著事件傳播處于激化點或事件沉寂點。在網絡結構層面，新媒體環境中事件的影響可被傳播廣度與傳播深度界定，NND指標以概率分布視角對傳播廣度深度進行了量化，使得不同類型不同結構網絡可進行網絡結構特征比較。連續計算NND指標并找出其突變點，即能夠揭示并定位事件傳播網絡中的關鍵節點與轉折節點，可在輿情檢測中準確地預測輿情爆發點，從而精準地制定并實施輿情疏控措施。

另一方面，模型重構了文本分布網絡。傳統的事件網絡結構基于具體的用戶信息行為，網絡中的文本關系不明確。本文對事件文本進行重構，在真實網絡結構的基礎上完成了文本分布網絡。同時針對該網絡的相似度計算同樣基于熵的概念，故具有跨事件可比性。模型保留了事件文本特征忽略了文本的具體內容，因此可發現事件更加隱性的特征，對傳統方法進行補充，如圖8所示。同時，內容分布NND基于事件傳播結構的內容相似度重構網絡，暗示了事件內部輿情討論的激烈程度。在內容分布層面，新媒體環境中事件的輿情沖突、復雜性由用戶發表內容之間觀點的認同與否共同決定。內容分布的NND指標在重構內容分布網絡的基礎上，量化了事件內部的輿情復雜性，可揭示事件討論觀點沖突的關鍵點。連續計算內容分布NND指標即可揭示事件輿情變化。通過識別挖掘新媒體傳播事件中的隱性內容，對提升輿情把控與識別能力、通過量化事件內部輿情復雜性對新媒體事件研判等具有實踐意義。整體而言對政府、企業等部門的形象公關、重大突發事件有效的防控把握、宣傳工作開展、政務新媒體工作部署等也具有應用價值。

5?總?結

傳統網絡事件相似度計算模型或聚類模型局限于事件表層特征且難以構建跨事件的統一相似度度量指標。本文從網絡結構、文本分布兩個維度出發，結合事件規模、文本一致性、網絡結構一致性等特征構建了基于熵的跨事件網絡事件相似度度量模型。使用聚類方法對本模型提出的相似度方法與傳統方法進行比較，結果表明本模型能夠補充和發現目前指標的缺點和劣勢。

理論方面，模型對現有網絡事件相似度大量的指標方法進行補充和完善。模型基于事件網絡結構熵與事件內容分布熵捕捉事件更深層次的信息，同時模型對于熵的度量具有天然可比性，使得模型能夠完成跨事件相似度對比。模型在文本分布層面進行文本分布網絡構建，使得微博類網絡事件能夠在傳統網絡結構基礎之上重構出基于內容相似的文本分布網絡，重構文本上下文性關系。

實踐方面，模型提出的方法可以對日后輿情事件分析、預測、分類等領域提供事件特征的基本指標，這種基于熵的指標可以對現有指標進行補充和修正。同時，模型對于文本分布網絡的重構可以進行進一步的擴展和完善，使得輿情平臺或者輿情處理方法能夠更加多元化和合理化。

參考文獻

[1]傅湘玲，齊佳音，高威.基于微博用戶創作內容的新聞線索自動發現研究[J].情報學報，2016，35（10）：1038-1047.

[2]王彥慈.基于云計算的微博輿情流式快速自聚類方法研究[J].情報科學，2017，35（8）：23-27.

[3]高慧穎，魏甜，劉嘉唯.基于用戶聚類與動態交互信任關系的好友推薦方法研究[J].數據分析與知識發現，2019，3（10）：66-77.

[4]吳恒，陳燕翎.基于UGC文本挖掘的游客目的地選擇信息研究——以攜程蜜月游記為例[J].情報科學，2017，35（1）：101-105.

[5]張海濤，唐詩曼，魏明珠，等.多維度屬性加權分析的微博用戶聚類研究[J].圖書情報工作，2018，62（24）：124-133.

[6]Wu L，Hoi S C，Yu N.Semantics-preserving Bag-of-Words Models and Applications[J].IEEE Transactions on Image Processing，2010，19（7）：1908-1920.

[7]Zhang W，Yoshida T，Tang X.A Comparative Study of TF*IDF，LSI and Multi-words for Text Classification[J].Expert Systems with Applications，2011，38（3）：2758-2765.

[8]路永和，李焰鋒.改進TF-IDF算法的文本特征項權值計算方法[J].圖書情報工作，2013，57（3）：90-95.

[9]安璐，周亦文.恐怖事件情境下微博信息與評論用戶的畫像及比較[J].情報科學，2020，38（4）：9-16.

[10]官賽萍，靳小龍，徐學可，等.基于WMD距離與近鄰傳播的新聞評論聚類[J].中文信息學報，2017，31（5）：203-214.

[11]翟姍姍，潘英增，胡畔，等.UGC挖掘中的在線醫療社區分面體系構建與實現[J].圖書情報工作，2020，64（9）：114-121.

[12]Cha M，Haddadi H，Benevenuto F，et al.Measuring User Influence in Twitter：The Million Follower Fallacy[J].Icwsm，2010，10（10-17）：30.

[13]Suh B，Hong L，Pirolli P，et al.Want to Be Retweeted？Large Scale Analytics on Factors Impacting Retweet in Twitter Network[C]//2010 IEEE Second International Conference on Social Computing，2010：177-184.

[14]林云，曾振華，曾林浩.微博社區網絡結構特征對輿情信息傳播的影響研究[J].情報科學，2019，37（3）：55-59.

[15]Celik M，Dokuz A S.Discovering Socially Similar Users in Social Media Datasets Based on Their Socially Important Locations[J].Information Processing & Management，2018，54（6）：1154-1168.

[16]Zhou X，Liang X，Du X，et al.Structure Based User Identification Across Social Networks[J].IEEE Transactions on Knowledge and Data Engineering，2018，30（6）：1178-1191.

[17]Jiang L，Yang C C.User Recommendation in Healthcare Social Media By Assessing User Similarity in Heterogeneous Network[J].Artificial Intelligence in Medicine，2017，81：63-77.

[18]Li Y，Su Z，Yang J，et al.Exploiting Similarities of User Friendship Networks Across Social Networks for User Identification[J].Information Sciences，2020，506：78-98.

[19]田世海，董月文，王健.基于NRL和k-means的輿情事件聚類研究[J].情報科學，2020：1-7.

[20]Miller G A.WordNet：A Lexical Database for English[J].Communications of the ACM，1995，38（11）：39-41.

[21]Lee J C，Cheah Y-N.Paraphrase Detection Using Semantic Relatedness Based on Synset Shortest Path in WordNet[C]//2016 International Conference on Advanced Informatics：Concepts，Theory and Application（ICAICTA），2016：1-5.

[22]Lee Y Y，Ke H，Yen T Y，et al.Combining and Learning Word Embedding with WordNet for Semantic Relatedness and Similarity Measurement[J].Journal of the Association for Information Science and Technology，2020，71（6）：657-670.

[23]Kusner M，Sun Y，Kolkin N，et al.From Word Embeddings to Document Distances[C]//International Conference on Machine Learning，2015：957-966.

[24]Landauer T K，Foltz P W，Laham D.An Introduction to Latent Semantic Analysis[J].Discourse Processes，1998，25（2-3）：259-284.

[25]Hofmann T.Probabilistic Latent Semantic Analysis[J].arXiv Preprint arXiv：1301.6705，2013.

[26]Blei D M，Ng A Y，Jordan M I.Latent Dirichlet Allocation[J].Journal of Machine Learning Research，2003，3（1）：993-1022.

[27]Gabrilovich E，Markovitch S.Computing Semantic Relatedness Using Wikipedia-based Explicit Semantic Analysis[C].IJcAI，2007：1606-1611.

[28]Schieber T，Carpi L，Diaz-Guilera A，et al.Quantification of Network Structural Dissimilarities[J].Nature Communications，2017，（8）：13928.

[29]Vallender S.Calculation of the Wasserstein Distance Between Probability Distributions on the Line[J].Theory of Probability & Its Applications，1974，18（4）：784-786.

[30]Grover A，Leskovec J.Node2vec：Scalable Feature Learning for Networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2016：855-864.

[31]Maaten L V D，Hinton G.Visualizing Data Using t-SNE[J].Journal of Machine Learning Research，2008，9（11）：2579-2605.

（責任編輯：孫國雷）