直擊圓錐曲線最值問題的解題策略

■江蘇省太倉市明德高級中學(xué)

圓錐曲線的最值(范圍)問題，因考查知識容較多、分析能力要求高、區(qū)分度高而成為高考命題的一個熱點。由于這類問題解法靈活且綜合性較強，故而成為高考的一大難點。那么，突破這一難點有哪些基本策略呢? 下面舉例說明。

一、利用圓錐曲線定義

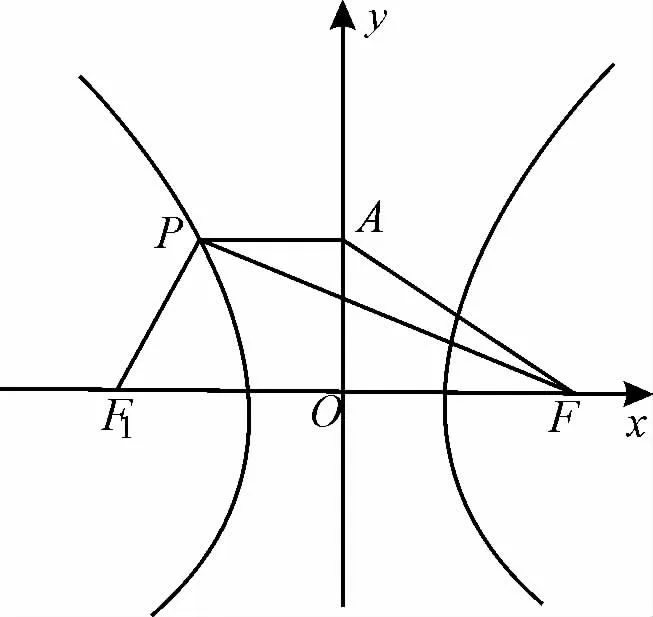
圖1

例1如圖1，已知點P在離心率為2 的雙曲線=1的左支上，A(0，)，F(xiàn)是 雙 曲 線 的 右 焦點，若△PAF周長的最小值是20，則此時△PAF的面積為( )。

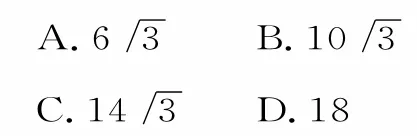
解析：先由雙曲線的定義可知△PAF周長的最小值等于|AF1|+|AF|+2a，再根據(jù)離心率的值可求出雙曲線方程，然后直線AF1與雙曲線聯(lián)立即可求出P點的坐標(biāo)，最后利用S△PAF=S△AF1F-S△PF1F求出面積。

設(shè)雙曲線的左焦點為F1，由題可知，|PF|-|PF1|=2a，|PF|=2a+|PF1|。

圖2

如圖2，△PAF的周長=|AP|+|PF|+|AF|=|AP|+|PF1|+|AF|+2a≥|AF1|+|AF|+2a，當(dāng)且僅當(dāng)A，P，F(xiàn)1三點共線時取等號。

因此，|AF1|+|AF|+2a=20。

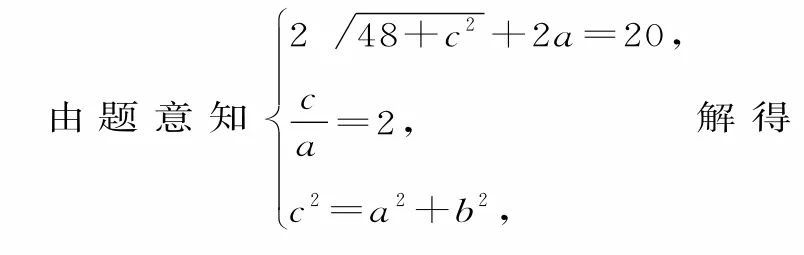
點評：對于某些橢圓或雙曲線中的最值問題，通常利用定義把到左焦點的距離轉(zhuǎn)化為到右焦點的距離，反之亦然;對于拋物線中的最值問題，同樣可依據(jù)定義把到焦點的距離轉(zhuǎn)化為到準(zhǔn)線的距離，反之亦然。這些方法的本質(zhì)是利用幾何關(guān)系求最值。

二、利用基本不等式

例2(1)拋物線y2=2px(p＞0)的焦點為F，已知點A，B為拋物線上的兩個動點，且滿足∠AFB=120°。過弦AB的中點M作拋物線準(zhǔn)線的垂線MN，垂足為N，則的最大值為( )。

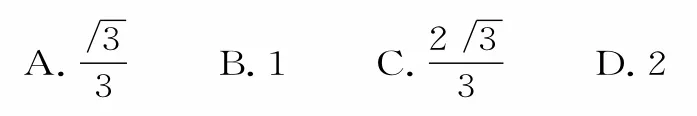
(2)設(shè)拋物線y2=2x的焦點為F，過F的直線交該拋物線于A、B，則|AF|+4|BF|的最小值為_____。

點評：當(dāng)依據(jù)題意得到關(guān)于求最值的表達(dá)式含有兩個未知數(shù)時，一般利用基本不等式求最值，但必須先要判斷是否滿足“一正二定三相等”。

三、轉(zhuǎn)化為函數(shù)的最值問題

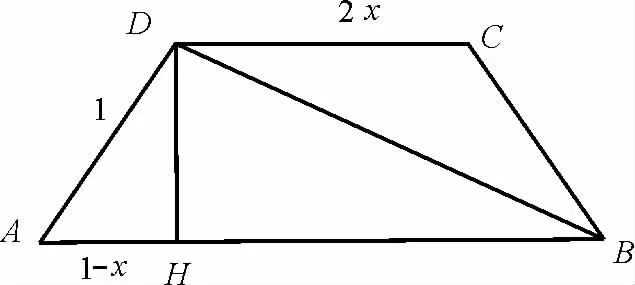
圖3

例3在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x，其 中x∈(0，1)。以A，B為焦點且過點D的雙曲線的離心率為e1，以C，D為焦點且過點A的橢圓的離心率為e2，若對任意x∈(0，1)，不等式t＜e1+e2恒成立，則t的最大值為( )。

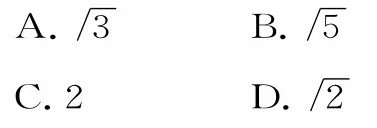
解析：在等腰梯形ABCD中，由余弦定理得：

點評：依據(jù)題意建立目標(biāo)函數(shù)時，一定要注意自變量的取值范圍，同時注意在求函數(shù)的最值時，遇到復(fù)雜函數(shù)采用換元法可以化繁為簡，還要關(guān)注函數(shù)的單調(diào)性。

鞏固練習(xí)

1.已知點R(0，2)，曲線C：y4=(px)2(p＞0)，直線y=m(m＞0且m≠2)與曲線C交于M，N兩點，若△RMN周長的最小值為2，則p的值為( )。

A.8 B.6

C.4 D.2

2.已知F1，F(xiàn)2是橢圓和雙曲線的公共焦點，P是它們的一個公共點，且∠F1PF2=，則橢圓和雙曲線的離心率乘積的最小值為_____。