曲柄搖桿機構的急回程度分析與探討*
馮立艷,梁會碩,蔡玉強,張雪雁,崔冰艷,李學剛,李建功,李德勝
(華北理工大學機械工程學院,河北 唐山 063210)
0 引言
當鉸鏈四桿機構的最短桿與最長桿長度之和小于或等于其余兩桿長度之和,且最短桿為連架桿時,則為曲柄搖桿機構。 曲柄搖桿機構能夠實現曲柄整周轉動與擺桿往復擺動之間的運動傳遞,有些場合,例如攪拌機、雷達天線俯仰搜索機構和顎式破碎機等,利用其急回特性可以縮短非工作時間,提高工作效率,同時生活中也出現了像空調的擺風機構、 電風扇的搖頭機構等這種去程和回程都是工作行程的機器,所以對曲柄搖桿急回特性的研究很有必要。
1 極位夾角的探討及急回運動分析
現在大多數的《機械原理》教材中對于極位夾角θ 的定義一般如下: 搖桿處于兩極限位置時曲柄兩對應位置所夾的銳角[1]。 然而,這并不準確,極位夾角的可能取值應是零度、銳角、直角和鈍角。 在文獻[2]中作出了明確定義:當從動件處于兩個極限位置時,對應曲柄的一個位置與另一個位置的反向延長線間所夾的角度。
曲柄搖桿機構的四個桿長滿足一定關系式時,極位夾角的取值可以在[0°,180°)之間[3],推導如下:

圖1 曲柄搖桿機構
圖1 中,曲柄 AB、連桿 BC、搖桿 CD 和機架 AD 的長度依次用 a、b、c、d 表示,φ 是搖桿的擺角,∠C1AC2為極位夾角。 令∠ADC2=α,∠ADC1=β,則 α=β+φ。
式(1)(2)(3)聯立得,

圖1 所示機構具有急回特性,分析如下:當搖桿從左極限位置DC1運動到右極限位置DC2,再運動到DC1,即曲柄從AB1到AB2,再回到AB1的過程中,曲柄兩個過程的角度相差2θ,所用的時間是不同的。 而搖桿轉動的角度即擺角是相同的,所以導致搖桿兩次擺動的角速度不相等。 亦即輸出件的反行程快于它的正行程。
通常用行程速比系數K 來描述機構急回的程度,即

其中:極位夾角θ 等于零時,K=1,機構無急回;極位夾角θ不等于零時,K>1,且K 值越大,急回程度越大。
2 曲柄搖桿機構的分類及各自的桿長關系
曲柄搖桿機構可能無急回特性,也可能有急回特性,其中有急回特性的曲柄搖桿機構分為Ⅰ型和Ⅱ型兩種。搖桿工作行程(慢行程)時的轉向與曲柄轉向相同時,稱為Ⅰ型機構;反之,則稱為Ⅱ型機構[4]。
Ⅰ型曲柄搖桿機構的特點是A、D 兩點在C1C2直線的同側;Ⅱ型機構的A、D 兩點在C1C2直線的異側[5]。
2.1 無急回特性的曲柄搖桿機構
極位夾角θ=0°,即搖桿CD 處于左右兩極限位置時,此時 AB1C1和 AB2C2共線[6],如圖 2 所示。

圖2 無急回特性的曲柄搖桿機構
當 θ=0°,由圖可知 E 點為 C1C2的中點,有

聯立得,a2+ d2= b2+ c2,即無急回(K=1)的曲柄搖桿機構應滿足的桿長關系。
2.2 Ⅰ型和Ⅱ型曲柄搖桿機構
因Ⅰ型曲柄搖桿機構的極位夾角θ 可能為銳角,也可能為鈍角,故圖3 繪出θ 為銳角、直角、鈍角三種情況下搖桿的極限位置與對應的曲柄位置。 圖中E、F 點為搖桿CD的兩個極限位置或其延長線與圓的交點[7]。


圖3 Ⅰ型曲柄搖桿機構
在△ADC1中,

在△ADC2中,

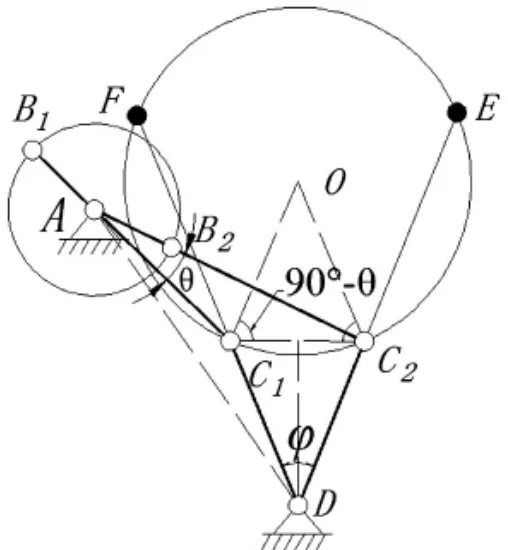
因Ⅰ型曲柄搖桿機構 (圖 3a、b 和 c) 中∠C1AD>∠C2AD,則 cos∠C1AD 因Ⅱ型曲柄搖桿機構的∠C1AD<∠C2AD,則 cos∠C1AD>cos∠C2AD,聯立式(6)和式(7)并化簡,如圖 4 所示,得Ⅱ型曲柄搖桿機構各桿長關系為: 圖4 Ⅱ型曲柄搖桿機構 圖5 最大極位夾角 如圖3 所示,隨著極位夾角θ 從銳角過渡到鈍角,搖桿CD(或其延長線C1F、C2E)不斷靠近圓的位置。 此時就會出現一個極限位置,即當搖桿CD 與圓O 相切,此時C1點和 F 點重合,C2點和 E 點重合,如圖 5 所示,這種情況下的極位夾角θ 即是最大值[8]。 基于ADAMS 軟件對上述各種情況的曲柄搖桿機構桿長條件進行了三維動畫的制作及仿真,得以進一步驗證。 表1 是Ⅰ型曲柄搖桿機構行程速比系數K 和φ 搖桿擺角三種不同取值下的桿長關系。 圖6 是三種情況下的動畫仿真截圖,其中桿AB 為曲柄,桿BC 為連桿,桿CD為搖桿,桿AD 為機架。 表1 曲柄搖桿機構 (單位:mm) 圖6 曲柄搖桿機構動畫仿真 在ADAMS 中成功仿真之后,進行后處理。 以曲柄轉角為橫坐標,搖桿角速度和角加速度分別為縱坐標,得出如圖7 的關系曲線圖。 因曲柄AB 勻速轉動,由圖可知當搖桿角速度為正與負時,所對應曲柄轉角的比值為行程速比系數K。 圖7 曲柄搖桿的搖桿角速度、角加速度—曲柄轉角的關系 通過三維動畫的運行仿真以及曲線圖,驗證了上述研究理論。 1)文章探討了極位夾角θ 的準確意義,分別推導出有無急回特性的曲柄搖桿機構的桿長關系。 2)推導出Ⅰ、Ⅱ型曲柄搖桿機構極位夾角θ 及行程速比系數K 的取值范圍。 3)運用Adams 軟件對Ⅰ型曲柄搖桿機構的三種極位夾角情況進行了驗證。
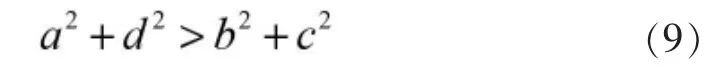
3 Ⅰ型和Ⅱ型曲柄搖桿機構極位夾角θ 和行程速比系數K 的最大值


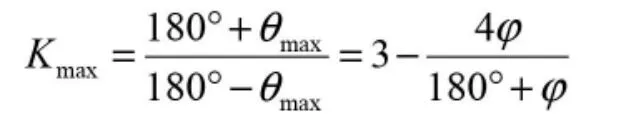
4 算例




5 結論

