IDC 機柜結構地震工況非線性時程分析研究*

馮 卉，杜文嫚，張朋波

（1. 中興通訊股份有限公司，江蘇南京210000；2. 信通院（保定）科技創新研究院，河北保定071000）

引 言

中國已進入大數據時代，巨大的數據價值勢必對互聯網數據中心（Internet Data Center, IDC）機房設備的抗震性能和可靠性提出更高的要求。機柜是IDC 機房的一個重要組成部分，其作用是方便安裝和固定服務器等IT 設備。當前對IDC 機柜的承載能力要求高，但在高承載工況下，IDC 機柜缺少相應的抗震設計，抗震性能差，設備傾倒、結構開裂、門板打開和連接失效等問題突出。

目前振動仿真分析技術通常采用線性振動理論和仿真分析模塊，無法正確模擬接觸這樣的典型非線性問題，導致仿真與實際誤差較大，無法真正指導設計。非線性振動技術是解決恢復力與位移不成線性比例關系或阻尼力與速度不成線性比例關系的振動問題的技術。

為了較為準確地解決地震載荷作用下IDC 機柜結構產生的大變形和高應力問題，本文以IDC 機柜為研究對象，采用Radioss 求解器進行非線性時程計算，并且進行物理樣機的抗震試驗，在與試驗數據對比的基礎上不斷修正分析模型，研究IDC 機柜模型的動力響應。

1 非線性時程分析

顯示時程分析法通常采用中心差分法。中心差分法用有限差分代替位移對時間求導（即速度和加速度）。如果采用等時間步長，則速度˙u 和加速度¨u 的中心差分近似為：

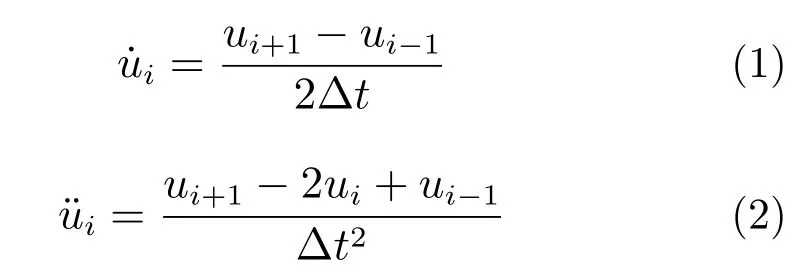
而離散時間點的運動為：

ui=u(ti), ˙ui= ˙u(ti), ¨ui= ¨u(ti), (i=0,1,2,···)

體系的運動方程為：

式中：m,c,k 為系數；u 為位移；t 為時間；P 為系統受到的外力。

將速度和加速度的差分近似公式（1）和（2）帶入由式（3）給出的ti時刻的運動方程可以得到：

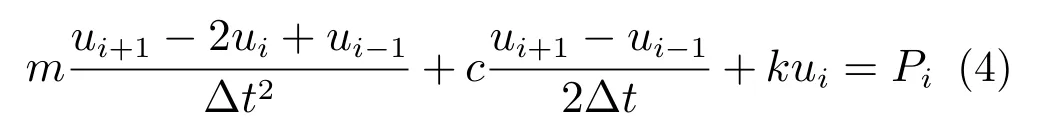
在式（4）中，假設ui和ui?1已知，即ti時刻及以前的運動已知，則可以整理方程得到：

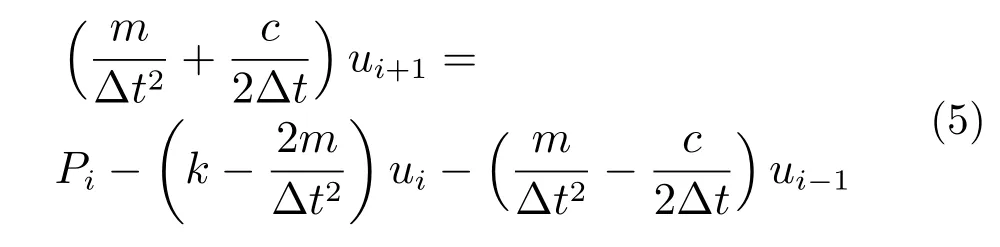
由式（5）就可以根據ti時刻及以前的運動求得ti+1時刻的運動。式（5）即為結構動力反應分析的中心差分法逐步計算公式。

2 地震波處理

本文地震波選取依照YD 5083—2005《電信設備抗地震性能檢測規范》中8 烈度、非電源類設備規定，由樓面反應譜根據隨機相位法生成人工合成地震波，地震加速度峰值為0.66g（g =9 800 mm/s2），持續時間為30 s，強震部分持續20 s。計算加載前，對地震波加速度數據進行基線校準和高通濾波，避免加速度信號通過積分求速度、位移時，原始基線漂移逐步放大，導致分析結果出現基線漂移。處理后的地震波加速度、速度和位移信號見圖1。

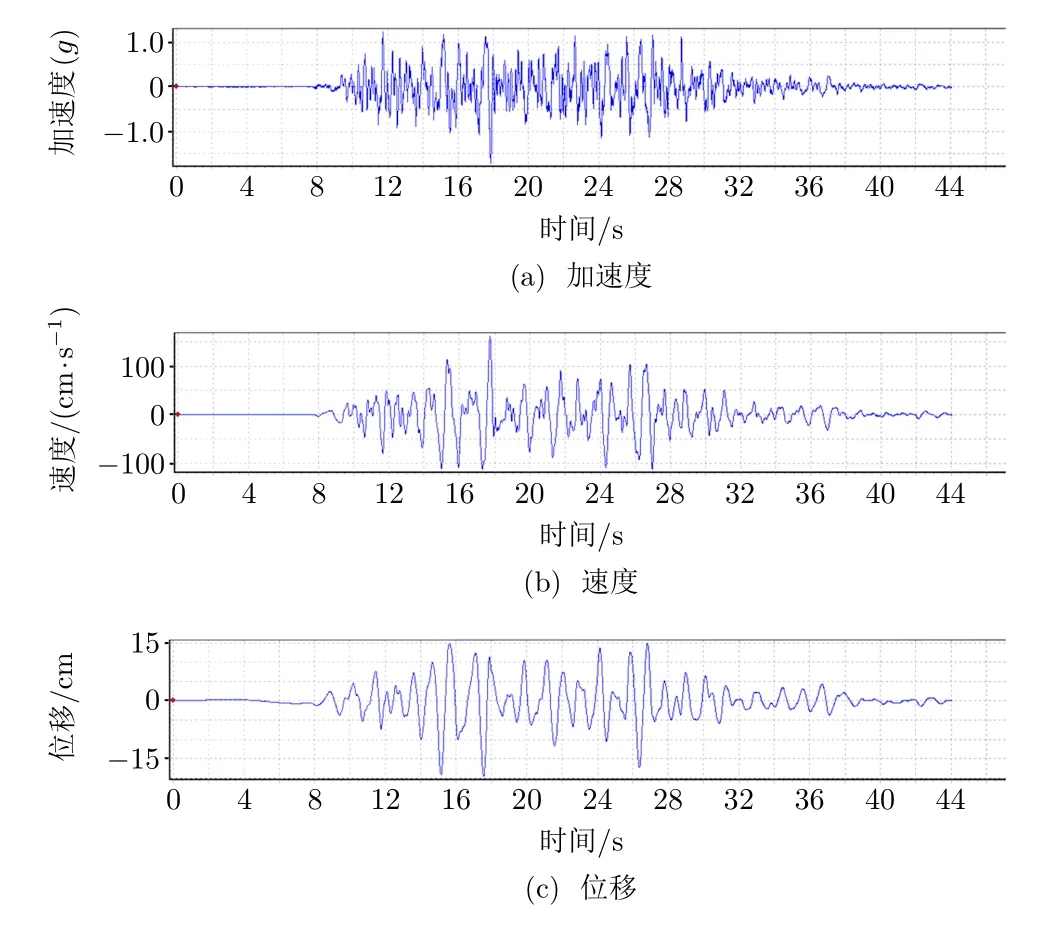
圖1 8 烈度、非電源類設備地震波加速度、速度和位移曲線

3 有限元建模

3.1 材料模型

本文采用最經典的彈塑性動力學材料模型——Johnson-Cook 材料模型。在此材料模型中，材料達到塑性之前，其真實應力按楊氏模量計算，達到塑性之后，材料的真實應力表達為塑性應變、應變率和溫度的函數，即：

式中：σ 為真實應力；εp為塑性應變；a 為屈服強度；b 為硬化模量；n 為硬化指數；c 為系數；ε 為參考應變；ε0為試驗應變；T 為溫度；m 為熱軟化指數。

本文工況忽略第2 部分應變率和第3 部分溫度變化的影響。第1 部分參數a，b，n 的確定過程為：在軟件中提供材料屈服應力σy，最大拉伸應力σUTS（由工程應力-工程應變曲線得到）和其對應的工程應變εUTS3 個參數，自動求解計算。

取機柜托盤結構作為拉伸試驗件，進行3 次拉伸試驗，得到3 條材料拉伸工程應力-應變曲線。取σy，σUTS和εUTS的平均值225 MPa，321 MPa 和0.2 進行分析。

3.2 材料失效本構

采用Radioss 材料本構中自帶的失效模式進行分析，需設置最大應力及材料斷裂時的應變。將3 條工程應力-應變曲線換算成真實應力-應變曲線，取值從真實應力-應變曲線得到，見表1。

表1 軟件設置冷軋鋼板材料參數

3.3 單元類型、網格尺寸與網格質量

在Hyper Mesh 中構建IDC 機柜抗震時程分析有限元模型，如圖2 所示。機柜主框架、內立柱、托盤等結構以平均單元尺寸8 mm 進行剖分，均采用二維單元P1-SHELL 進行離散。連接螺栓和焊接采用Rigid 單元模擬，在托盤與配重塊之間存在潛在接觸部位，采用Radioss Type7 接觸模型建立接觸對，并考慮摩擦影響。網格剖分共獲得223 574 個單元。三角形單元過于剛硬，模型中三角形單元的占比為0.05%，滿足精度要求。在邊緣處或有孔的結構中，任何方向上都至少有三層單元。

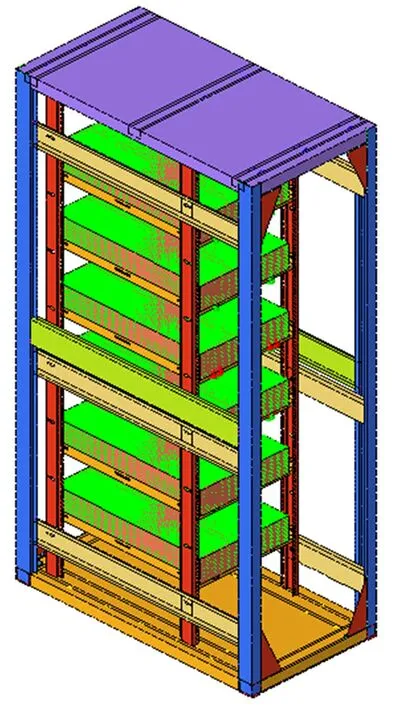
圖2 IDC 機柜有限元模型

3.4 沙漏能控制

顯示分析中采用縮減積分會造成沙漏能。縮減積分是指單元計算時積分點數少于實際個數，這種操作能加快計算速度，但是會造成一種單元的零能模式，這就是沙漏。計算要求沙漏能的占比在?15%～?10%之間。分析時，通過沙漏粘性阻尼算法進行控制，即施加一個與沙漏模態變形方向相反的沙漏阻尼力來抵御變形。分析模型的內能、沙漏能和總能曲線見圖3。沙漏能的最大占比為?3%，能保證計算結果穩定、準確。

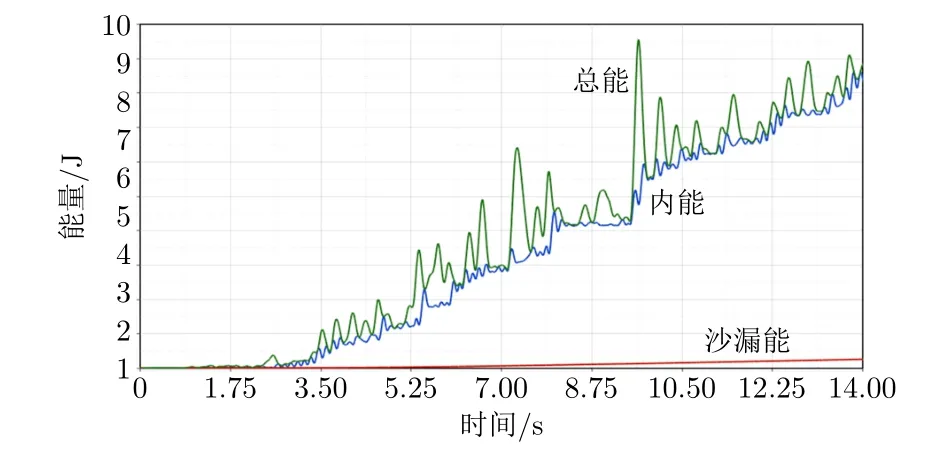
圖3 有限元模型內能、沙漏能和總能曲線

4 結果對比

4.1 評價指標

本文以地震試驗得到的位移數據為基準，以峰值和峭度2 個參數為評價指標，對試驗數據和分析數據進行對比，評價分析結果的準確性。

峰值是指信號時域圖中某一時刻的振幅最大值。峭度是反映隨機變量分布特性的數值統計量，是歸一化的4 階中心距，可以表示波形平緩程度，用于描述變量的分布。

4.2 仿真與試驗結果對比

4.2.1 變形現象對比

8 烈度地震載荷作用下最大位移時刻的變形結果的仿真與測試對比如圖4 所示。結構變形的仿真分析和試驗現象一致。

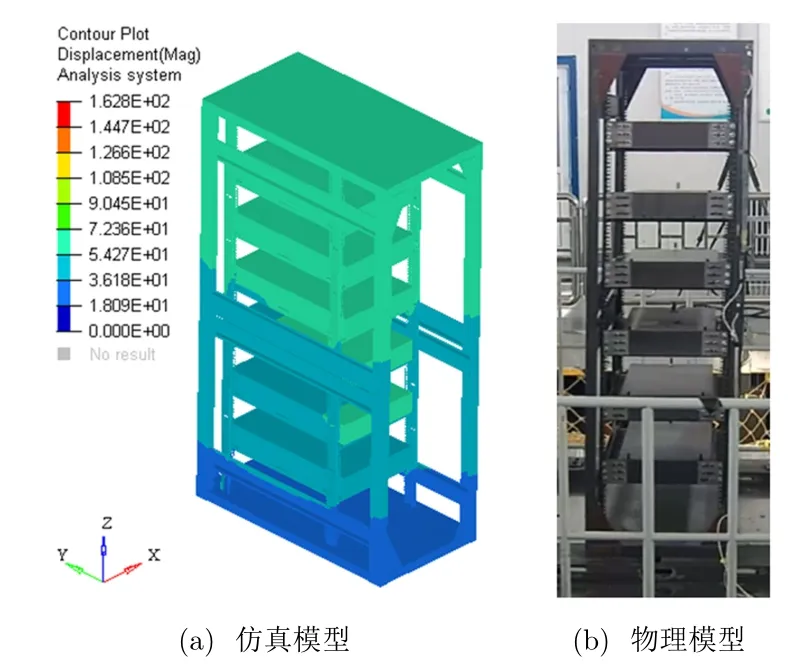
圖4 仿真和測試對比

4.2.2 位移峰值對比

讀取8 烈度工況下結構地震試驗位移和仿真分析位移數據，繪制曲線，如圖5 和圖6 所示。試驗位移峰值為37.8 mm，仿真分析位移峰值為33 mm，兩者相差12.7%。

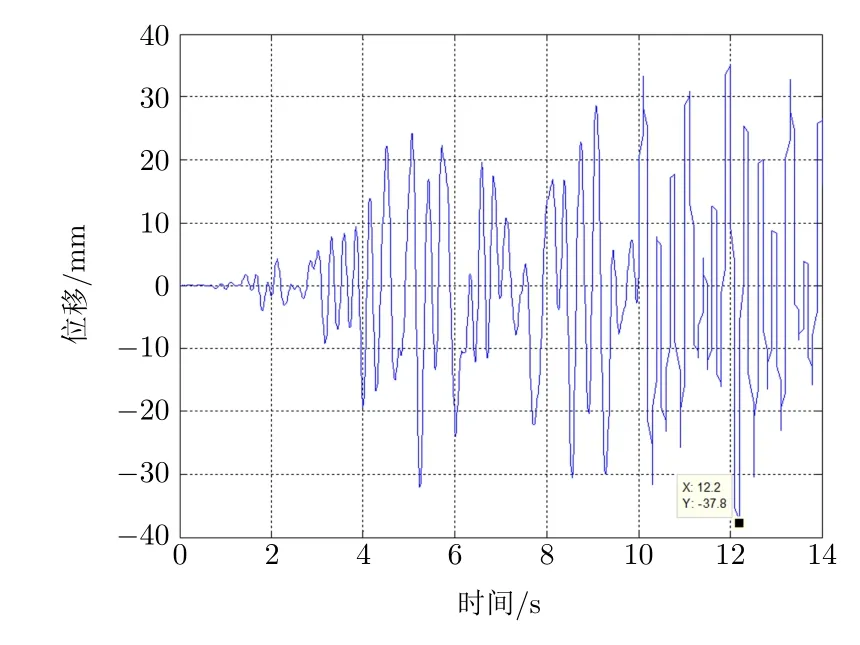
圖5 試驗位移曲線

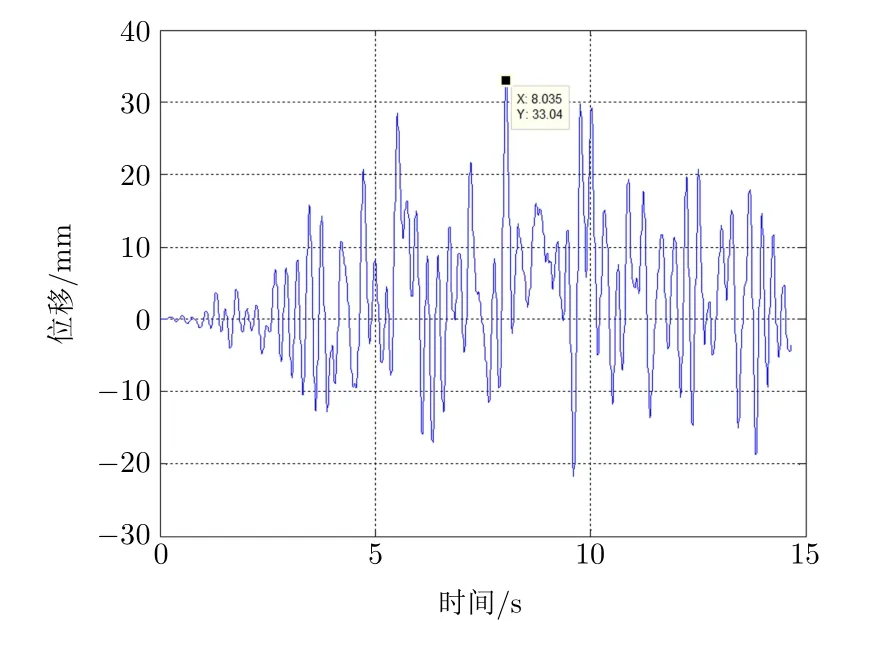
圖6 仿真分析位移曲線

4.2.3 峭度對比

分別對試驗數據和仿真分析數據進行峭度值計算，試驗峭度值為3.23，仿真分析峭度值為3.45。峭度指標值約為3，振動信號接近正態分布，試驗和仿真的信號分布一致，無較大的沖擊信號出現。

5 結束語

從IDC 機柜抗震仿真分析結果來看，仿真分析機柜變形趨勢接近機柜實際物理試驗狀態。

從試驗位移曲線和仿真分析位移曲線結果來看，兩條曲線的波形、趨勢、峰值和峭度基本吻合，表明IDC 機柜采用非線性時程分析方法可以準確模擬機柜在地震過程中的動力響應。

在IDC機柜抗震仿真與物理試驗對標研究中，網格尺寸、網格質量、材料模型、接觸和沙漏能控制是仿真結果與物理試驗對標的關鍵。通過有限元建模細節的控制，可使仿真分析結果接近試驗結果。

本文建立的非線性時程分析方法合理、準確，可有效模擬地震作用下結構的受力和真實狀態，在機柜抗震設計過程中可實現仿真驅動設計。同時，建模方法可以推廣到其他通信設備的非線性時程分析中。