一類時滯SDTR戒酒模型的局部漸近穩定性

張子振，張偉詩，宋志強

(1.安徽財經大學 管理科學與工程學院，安徽 蚌埠 233030；2.呼倫貝爾學院 機電工程學院，內蒙古 呼倫貝爾 021008)

近年來，隨著生活水平的提高，生活方式越來越多樣化，飲酒在人們的日常生活中扮演著越來越重要的角色。2018《中國飲酒人群適量飲酒狀況》白皮書數據顯示，我國飲酒人群高達6億[1]。然而，與之相應的與飲酒相關的各種疾病也大大增加,比如，脂肪肝、冠心病、酒精依賴綜合征、酒中毒性幻覺癥等,酗酒還會引起家庭暴力、酒后駕駛等社會不良問題[2]。因此，飲酒尤其是酗酒不僅是一個嚴重的全球性公共衛生問題，也是一個亟待解決的社會問題。為了控制酗酒行為傳播，近年來，一些研究學者開始借助于動力學系統模型研究酗酒行為的傳播規律，以便為控制酗酒行為的傳播提供參考性建議。Xiang等[3]提出了一類考慮移民影響的戒酒模型，通過構造合適的李雅普諾夫函數研究了模型的全局漸近穩定性。Ma和Huo[4]提出了一類考慮公共健康教育的戒酒模型，并研究了模型的全局漸近穩定性，分析了公共健康教育對酗酒行為傳播控制的影響。最近，文獻[5]研究了一類具有時滯的戒酒模型

(1)

其中:S(t)表示偶爾飲酒人群在時刻t的數量,D(t)表示酗酒人群在時刻t的數量,T(t)表示戒酒人群在時刻t的數量,R(t)表示成功戒酒人群在t時刻的數量;A，β1，β2，μ，η，δ1，γ，δ2，σ為模型(1)的參數，其具體含義可以參看文獻[5];τ表示戒酒人群成功戒酒需要的時間周期時滯。文獻[5]研究了時滯τ對模型(1)穩定性的影響，分析了模型(1)Hopf分岔的存在性。

受文獻[5]研究工作的啟發，并考慮到成功戒酒人群對酒精的臨時免疫力，本文考慮另外一種形式的時滯戒酒模型

(2)

其中，τ為成功戒酒人群對酒精的臨時免疫期時滯。

1 基本再生數

求解方程組

(3)

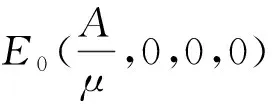
2 局部漸近穩定性

根據文獻[5]的分析可知，當R0>1時，模型(2)存在唯一飲酒平衡點E*(S*,D*，T*,R*),其中

其中D*是方程

(4)

的正根,式中

l1=Aβ1β2(μ+η)+β1ησγ-β1γ(μ+η)(μ+δ2+σ)-[β1(μ+δ2+σ)+β2μ](μ+η)(μ+δ1),

l2=-β1β2(μ+δ1)(μ+η),l0=μ(μ+η)(μ+δ2+σ)(μ+δ1+γ)(R0-1)。

顯然，l2<0。當R0>1時，l0>0。因此，當R0>1時，方程(4)存在唯一正根。進而可以得知，R0>1時，模型(2)存在唯一飲酒平衡點E*(S*,D*,T*,R*)。

模型(2)在E*(S*,D*,T*,R*)處的線性化部分為

(5)

相應的特征方程為

λ4+Γ3λ3+Γ2λ2+Γ1λ+Γ0+(Φ3λ3+Φ2λ2+Φ1λ+Φ0)e-λτ=0。

(6)

其中

μ(μ+β1D*)(β1S*+β2T*-μ-δ1-γ)(β2D*+μ+δ2+σ),

μ(μ+β1D*)(β2D*-β1S*-β2T*+2μ+δ1+δ2+σ+γ)-

(2μ+β1D*)(β1S*+β2T*-μ-δ1-γ)(β2D*+μ+δ2+σ),

μ(μ+β2D*)+(2μ+β1D*)(β2D*-β1S*-β2T*+2μ+δ1+δ2+σ+γ),

Γ3=(β1+β2)D*-β1S*-β2T*+4μ+δ1+δ2+σ+γ,

η(μ+β1D*)(β1S*+β2T*-μ-δ1-γ)(β2D*+μ+δ2+σ),

η(μ+β1D*)(β2D*-β1S*-β2T*+2μ+δ1+δ2+σ+γ),

Φ2=η(2μ+β1D*)(β1D*-β1S*+β2D*-β2T*+3μ+δ1+δ2+σ+γ),Φ3=η。

當τ=0時，方程(6)變為

λ4+(Γ3+Φ3)λ3+(Γ2+Φ2)λ2+(Τ1+Φ1)λ+Γ0+Φ0=0。

(7)

根據Routh-Hurwitz穩定性判據，當(Γ0+Φ0)>0，(Γ2+Φ2)(Γ3+Φ3)>(Γ1+Φ1)，且

(Γ1+Φ1)(Γ2+Φ2)(Γ3+Φ3)>(Γ0+Φ0)(Γ3+Φ3)2+(Γ1+Φ1)2

時，模型(2)局部漸近穩定。

當τ>0時，假設λ=iε(ε>0)為方程(6)的根，代入方程(6)分離實部和虛部，有

(8)

進而可以得到下列關于ε的代數方程

(9)

令

方程(9)變為

χ4+Δ3χ3+Δ2χ2+Δ1χ+Δ0=0。

(10)

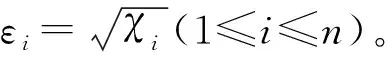
(11)

其中

對方程(6)兩邊求λ關于τ的導數，得到

因此

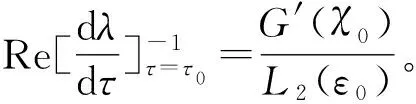
定理1對于模型(2)，如果R0>1，那么當τ∈[0,τ0)時，模型(2)局部漸近穩定；當τ=τ0時，模型(2)在飲酒平衡點E*(S*,D*,T*,R*)處產生Hopf分支。

3 數值模擬

選取A=0.7，β1=0.8，μ=0.25，η=0.45，β2=0.3，δ1=0.35，γ=0.4，δ2=0.3，σ=1.25。可以得到模型(2)的如下示例模型：

(12)

利用Matlab軟件計算得到R0=2.24>1，進而計算得到示例模型(12)的唯一飲酒平衡點

E*(1.2118,0.4936,0.1014,0.1811)。

當τ=0時，可以計算得到Γ0=0.1777，Γ1=1.1068，Γ2=1.9106，Γ3=2.8431，Φ0=0.3198，Φ1=0.7131，Φ2=1.1279，Φ3=0.45。進而可以驗證

(Γ0+Φ0)>0，(Γ2+Φ2)(Γ3+Φ3)>(Γ1+Φ1)，

(Γ1+Φ1)(Γ2+Φ2)(Γ3+Φ3)>(Γ0+Φ0)(Γ3+Φ3)2+(Γ1+Φ1)2。

因此，當τ=0時，示例模型(12)局部漸近穩定。仿真效果如圖1所示。

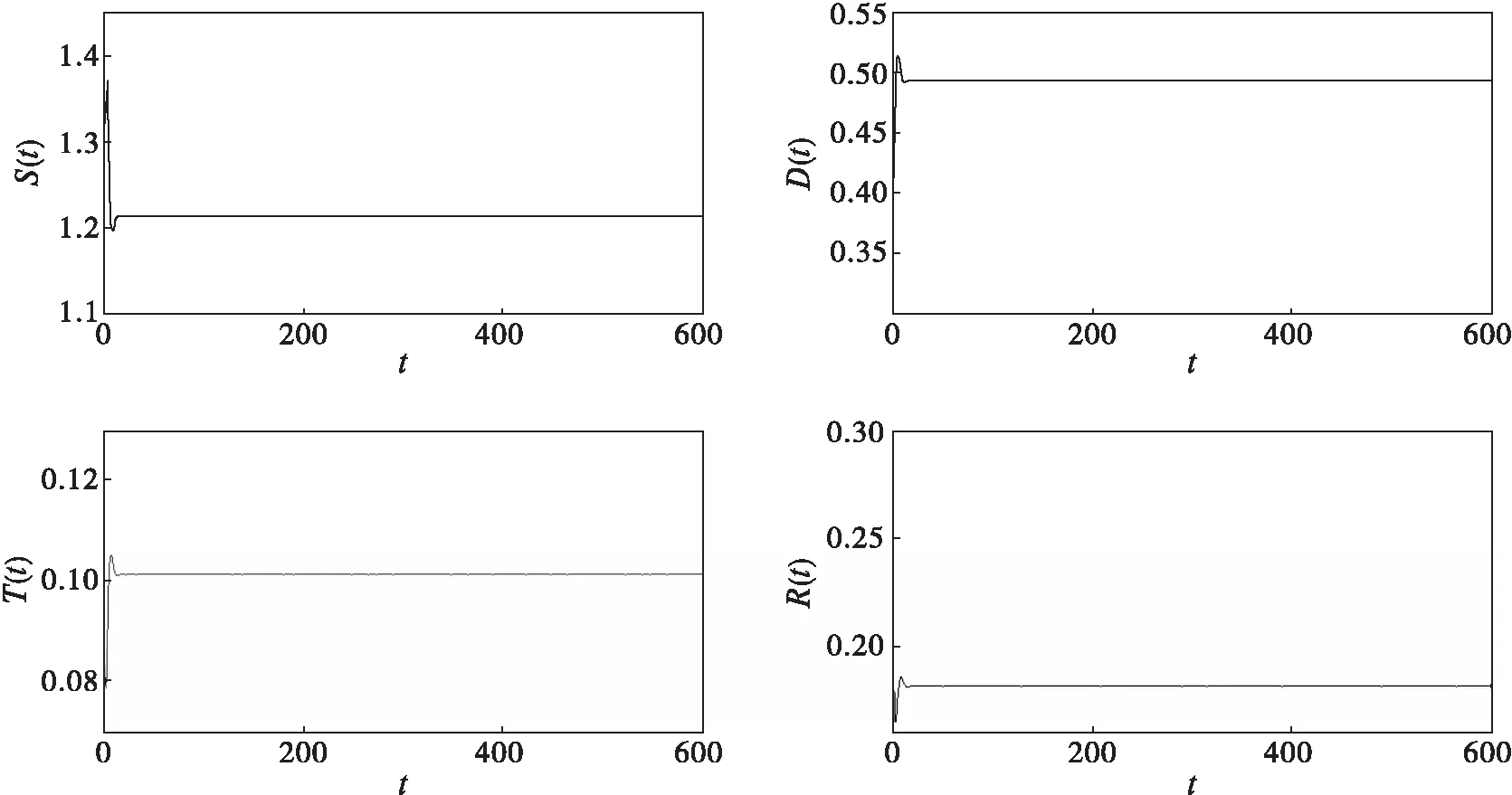
圖1 當τ=0時的仿真效果

當τ>0時，可以計算得到ε0=0.4631，τ0=8.0819，G′(χ0)=0.1068>0。因此，根據定理1可知，當τ∈(0,τ0)時，示例模型(12)局部漸近穩定，仿真效果如圖2所示。

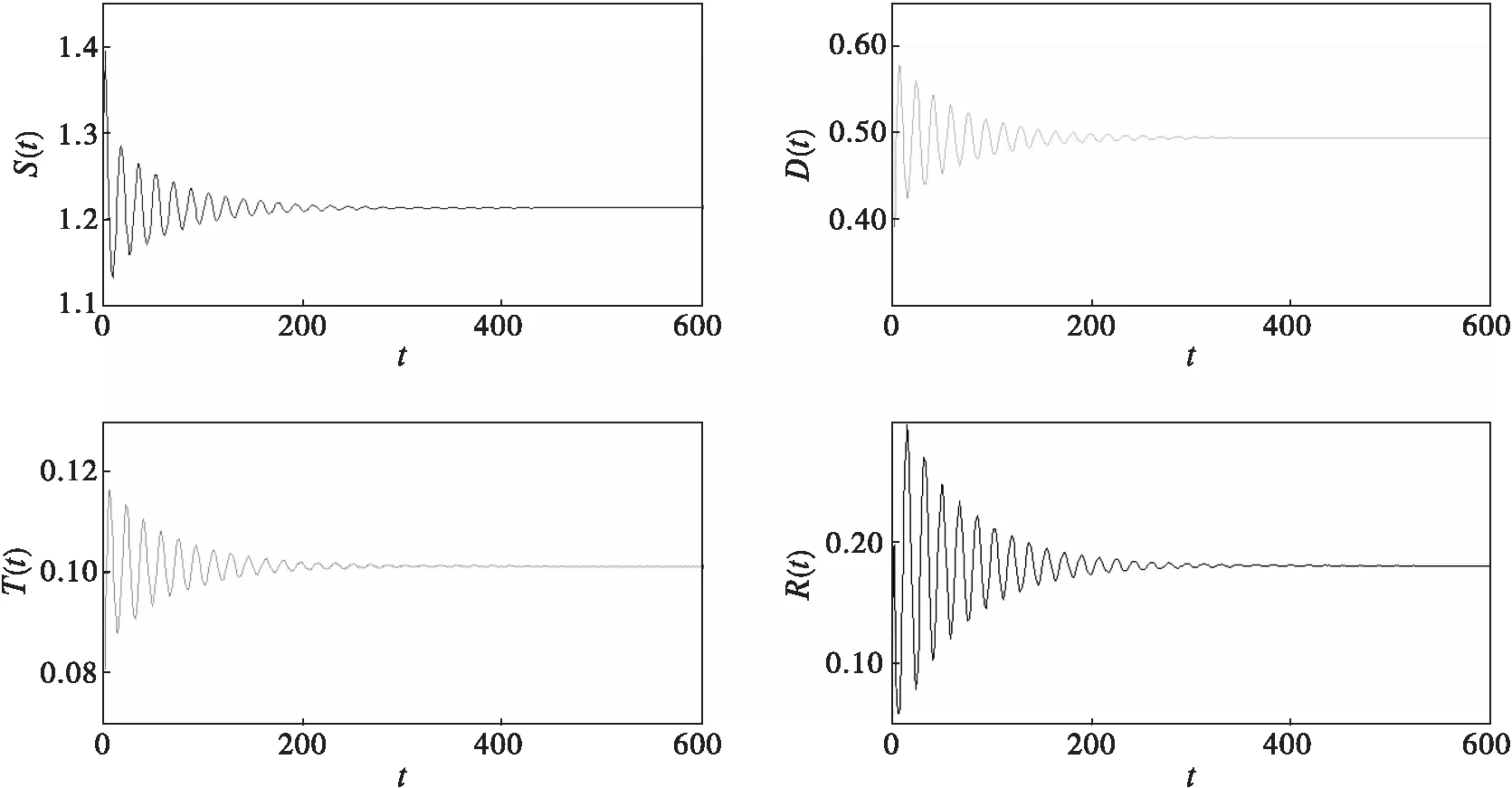
圖2 當τ=6.75∈(0,τ0)時的仿真效果

當τ=τ0時，示例模型(12)在E*(1.2118,0.4936,0.1014,0.1811)處產生Hopf分支，仿真效果如圖3所示。

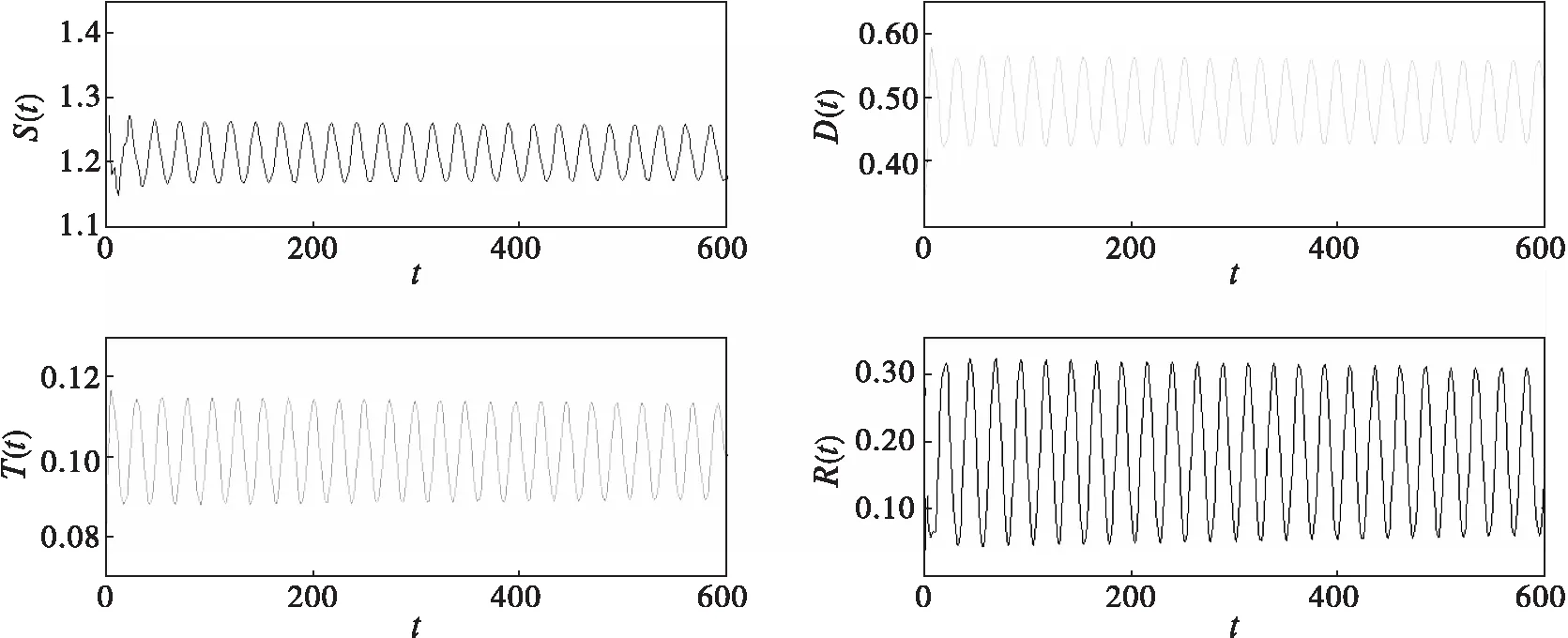
圖3 當τ=9.85>τ0時的仿真效果

4 小結

適度飲酒有利于幫助飲酒者緩解壓力和緊張情緒，然而過度飲酒甚至酗酒不僅會給飲酒者的身體帶來傷害，而且還會給社會治安帶來安全隱患。基于此，本文在文獻[5]的基礎上，研究了一類時滯SDTR戒酒模型。

首先計算得到模型的基本再生數，并計算得到模型的飲酒平衡點。進而以戒酒成功者對酒精的臨時免疫期時滯為分支參數，推導出模型局部漸近穩定和產生Hopf分支的充分條件。研究表明，戒酒成功者對酒精的臨時免疫期時滯越小(低于時滯臨界點τ0)，越有利于控制酗酒行為的傳播;而當戒酒成功者對酒精的臨時免疫期時滯超過臨界點τ0時，酗酒行為將失去控制。本文所得結果是對文獻[5]研究工作的適當補充。