一種改進的電力系統戴維南等值參數跟蹤算法

陳鑫楠，孫 淵

（上海電機學院機械學院，上海 201306）

近年來，電力系統向大電網、高電壓和遠距離輸電發展，在提高經濟效益的同時帶來了電力系統安全運行的新問題［1-3］。由于電網規模和負荷需求的不斷增加，電力系統逐漸接近穩定極限［4］。因此，電力系統電壓穩定性成為了研究的熱點。相量測量單元為電壓穩定的研究提供了新的手段，基于相量測量數據的戴維南等值參數在線辨識方法得到了廣泛的發展。由于戴維南等值參數受網絡拓撲和系統運行方式等影響，因此對其準確辨識是實現電網靜態穩定在線評估的關鍵［5］。

1999年，Vu等［6］首次運用本地相量測量數據求解戴維南等值參數，利用節點負荷阻抗與戴維南等值阻抗的關系進行電壓穩定性評估，并應用最小二乘法根據相鄰兩個采樣時刻測得的電氣量信息進行戴維南等值參數的估算。此后，國內外許多學者對戴維南等值參數的估計方法進行了研究與改進。肖俊等［7］就等值網絡擾動狀況下的戴維南等值參數辨識原理進行闡述，考慮利用擾動后的暫態分量進行等值參數辨識的方法。李東東等［8］對基于傳統法假設相鄰采樣時刻戴維南等值參數不變的情況進行了改進，僅假設相鄰時刻戴維南等值參數的幅值不變、相角可變，利用冪級數展開求解戴維南等值參數，避免了參數漂移的問題。葉平峰等［9］提出了考慮源網荷關聯特性的戴維南等值參數解析方法。上述方法均是基于兩個或多個時間斷面的數據進行戴維南等值參數辨識，要求相鄰時刻戴維南等值參數保持不變，在該情況下的算法對等值系統的擾動有一定的要求，當等值系統內部擾動較大或負荷側擾動過小時，常無法辨識準確的戴維南等值參數。

初值的選擇問題是單時間斷面算法的共同問題。朱良濤等［10］將全微分算法進行改進，提出初值優選環節，將前一時刻求出的等值參數作為下一時刻的計算初值進行迭代求解。崔馨慧［11］提出了一種基于廣域量測信息的大電網戴維南等值參數在線辨識方法，根據大電網的單狀態斷面數據，對整個系統進行LU分解，減少了參數辨識的時間。

偏最小二乘法常應用于電力系統公共耦合點處的諧波阻抗估計中。林順富等［12］提出一種基于改進快速獨立成分分析及偏最小二乘法的系統諧波阻抗估計方法，降低解混信號變量之間弱相關性帶來的計算誤差。范忠等［13］提出了一種基于三點篩選法與偏最小二乘法的系統諧波阻抗估計方法。張坤等［14］將偏最小二乘法應用于公共耦合點處的戴維南等值參數估計中，但僅考慮了算法適用于系統側基本不變而用戶側有較大波動的數據情況，未考慮其他擾動情況。

本文提出了一種基于復數域偏最小二乘法的電力系統戴維南等值參數跟蹤算法。該方法簡化了傳統偏最小二乘法的數學模型和算法流程，使迭代求解過程更加簡單。同時，該方法能夠改善參數漂移現象，甚至在等值系統內部存在擾動時也能穩定辨識出戴維南等值參數。通過IEEE 39節點系統進行仿真驗證了本文算法的有效性和準確性。

1 傳統戴維南等值參數計算解析

根據戴維南等值理論可知，任意線性系統在任一時間斷面可等值為一個電壓源與阻抗串聯的兩節點系統，如圖1所示。為表述簡便，將系統中除等值節點負荷以外的其他部分統稱為系統側，將包含等值負荷的一側稱為負荷側。

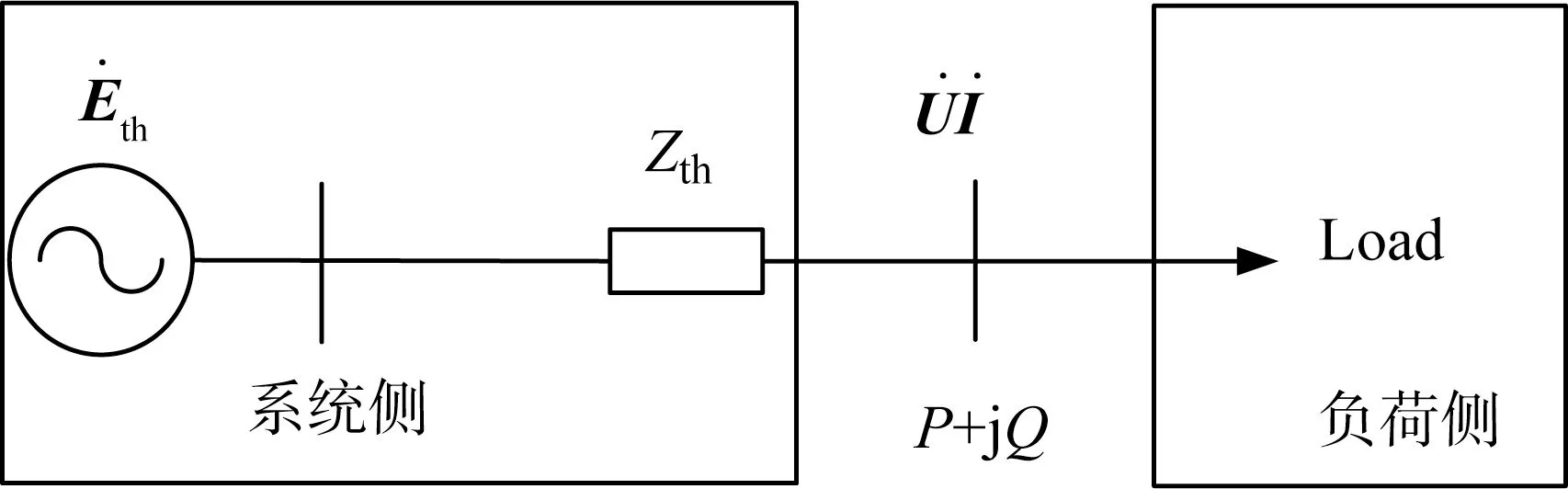
圖1 戴維南等值系統

根據基爾霍夫電壓定律可得

式中：為戴維南等值電勢；Zth為戴維南等值阻抗；˙為等值母線節點的電壓與電流的測量值。

根據傳統法的假設，相鄰采樣時刻戴維南等值參數不變，即可求出戴維南等值阻抗值為

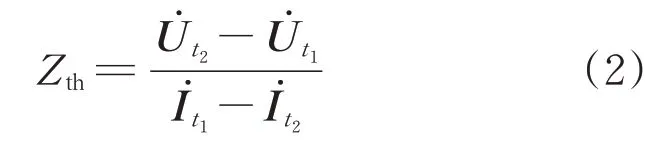
若上述假設需成立，要求系統在相鄰采樣間隔內負荷側有合適擾動，系統側擾動基本不變。若采樣間隔過于接近或負荷側擾動過小，則相鄰采樣間隔內電壓電流相量數值近似相等，式（2）會出現“0/0”的形式，出現參數漂移；若采樣時刻間隔過大，則上述假設不成立，無法計算戴維南等值參數；若只有系統內部發生擾動，依據傳統法計算得到的結果實際為負荷阻抗，求解的參數結果失效。

2 戴維南等值參數

2.1 偏最小二乘法原理

偏最小二乘回歸是一種新型的多元統計數據分析方法，該方法可以實現多因變量對多自變量的回歸建模［15］。特別是在自變量存在嚴重多重相關性時，用偏最小二乘法進行回歸分析，比傳統多元回歸分析更適合。偏最小二乘回歸模型更容易辨識系統中的信息和噪聲，對每一個自變量的回歸系數更容易解釋。

設自變量與因變量的數據表分別為：X=[x1，x2，…，x p]n×p，Y=[y1，y2，…，yq]n×q（p個 自變量，q個因變量，n個采樣點）。在回歸分析前，先將自變量、因變量標準化，得到X的標準化矩陣為E0，Y的標準化矩陣為F0。偏最小二乘回歸分別在E0、F0中提取成分t1和u1（兩者分別是p個自變量和q個因變量的線性組合）。t1=E0ω1，ω1為E0的第1個軸，‖ω1‖=1；u1=F0c1，c1為F0的第1個軸，‖c1‖=1。要求t1、u1滿足兩個要求：

（1）t1、u1應攜帶各自數據表中的變異信息；

（2）t1、u1的相關程度能夠達到最大。

上述要求可以轉化為t1、u1的協方差達到最大，即為：max cov(t1，u1)。根據拉格朗日算法轉化為求解矩陣的特征值和特征向量的問題。待求解矩陣如下：

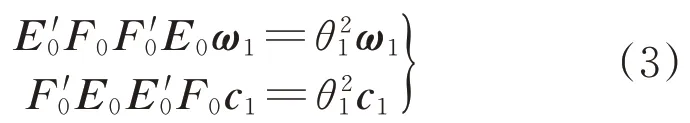
式中：ω1為E′0F0F′0E0矩陣取最大特征值θ21的特征向量；c1為F′0E0E′0F0矩陣取最大特征值θ21的特征向量。

在簡化偏最小二乘法中，只求取ω1，則回歸方程可以表示為

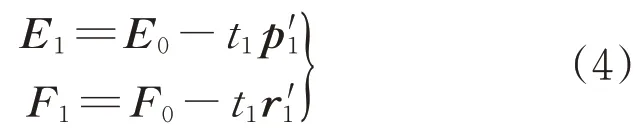
其中，

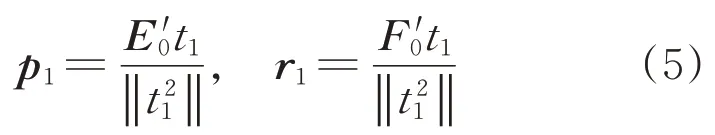
式中：E1、F1為殘差矩陣；p1、r1為回歸系數向量。

用殘差矩陣E1、F1代替E0、F0進行迭代求解。簡化偏最小二乘法只需用殘差矩陣E1代替E0，無需用F1代替F0，即可求解式（3）中的矩陣進而迭代求解。根據迭代精度要求，由交叉有效性確定提出m個成分，建立F0關于m個成分的回歸方程如下：

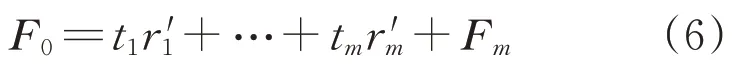
最后經標準化的逆運算，根據上述回歸方程求出因變量yi（i=1，2，…，p）關于自變量x i的回歸方程，即

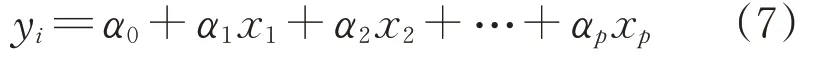
式中：αi（i=1，2，…，p）為所要求的原回歸系數。

2.2 基于傳統偏最小二乘法的數學模型

將式（1）中的電壓、電流等相量按實部、虛部展開為

式中：下標real、imag分別為相量的實部和虛部；Rth為戴維南等值電阻；Xth為戴維南等值電抗；Ereal、Eimag、Rth、Xth為待求的戴維南等值電勢和阻抗值。

選取自變量X為電流實部相反數和虛部形式，即為［-Iireal、I iimag］，因變量為節點電壓的實部和虛部，即為[U ireal、U iimag]，其中上標i代表量測次數。將式（8）擴展為

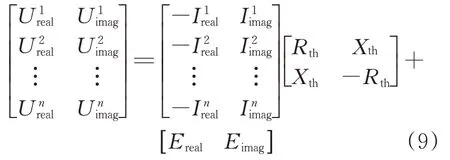
傳統偏最小二乘法常使用上述電壓電流相量實部虛部分離的矩陣形式進行戴維南等值參數的計算。應用多因變量的算法流程，計算復雜，且求解時間長，求解的戴維南阻抗矩陣的兩個電阻或電抗值常有偏差，參數的求解結果常存在誤差，造成求解不準確。

2.3 基于復數域偏最小二乘法的數學模型

復數域偏最小二乘法是將電壓、電流、電勢的復數形式代入式（1）中。由式（1）可得，=Ereal+jEimag為需要辨識的戴維南內電勢，˙=Ureal+jUimag為量測的節點電壓相量，˙=Ireal+jIimag為量測的節點電流相量，Zth=Rth+jXth為需要辨識的戴維南阻抗。根據復數域偏最小二乘法，選取自變量X為負荷節點電流復數形式［˙］，即為［-I ireal-jI iimag］，因變量Y為負荷節點電壓復數形式，即為［U ireal+jU iimag］。將式（1）擴展為

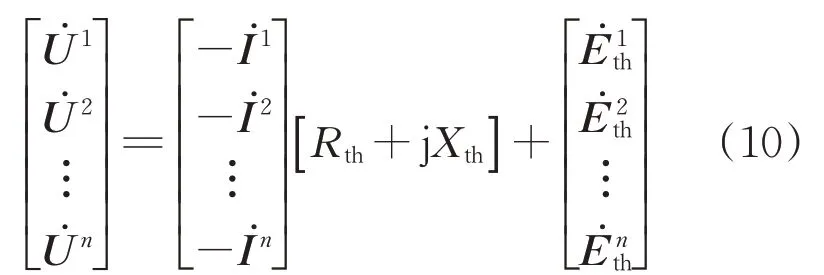
在計算戴維南等值參數時選取n次等值節點處電壓電流采樣值為一組數據，將采樣的電流、電壓的實部和虛部數據改寫成I˙、U˙的復數形式進行標準化，將標準化后的自變量E0和因變量F0代入式（3）中，求解矩陣特征值和特征向量，并進行成分t和殘差矩陣E1的求解；將E1代入式（3）進行迭代求解，直到滿足交叉有效性要求，求出所有成分得式（6）；根據標準化逆運算求出式（7）中回歸系數，求解得出的戴維南等值參數為復數形式。

傳統偏最小二乘法求解戴維南等值參數時，需對式（8）和式（9）中的阻抗矩陣進行求解。式（9）的表達式在求解時實際上運用了兩次基爾霍夫電壓定律。在求解的過程中要求|Ureal-f(Rth，Xth，Ereal)|以及|Uimag-f(Rth，Xth，Eimag)|的數值同時達到最小，相當于兩個函數的最小二乘誤差都最小。但兩個最小二乘誤差不能同時達到最小值，求得的電阻電抗值與準確值相比存在一定的誤差，無法正確地跟蹤戴維南等值參數，造成參數漂移問題。而運用復數域偏最小二乘法進行戴維南等值參數求解時，傳統方法中的公式簡化成了|U-f(Rth，Xth，Eth)|的求解過程，應用式（10）進行阻抗矩陣求解時，只需列寫一遍基爾霍夫電壓定律。因此，求解一個函數的最小值，無需在求解過程中均衡求解誤差，直接可以得到復數偏最小二乘法的極值。求解得到的極值點是明確的，可得到唯一的復數形式的阻抗值。與傳統偏最小二乘法相比，該算法可以得到更準確的戴維南阻抗值，有效地改善參數漂移的問題。

3 算例分析

本文在DIgSILENT/PowerFactory 15.0中搭建的IEEE 39節點標準系統，含有10臺發電機、39個節點、12臺變壓器和34條輸電線路。其系統拓撲結構如圖2所示。

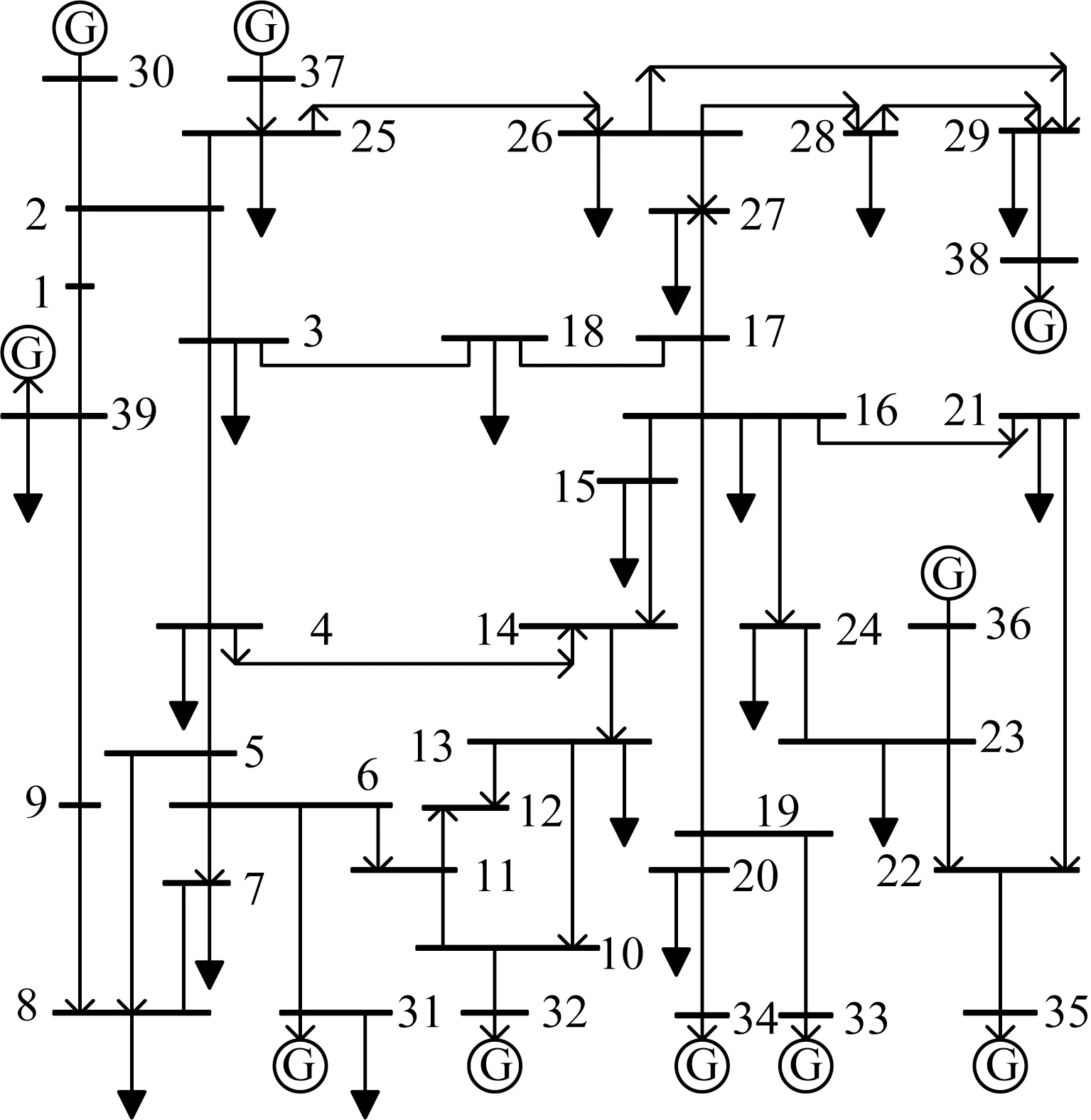
圖2 IEEE 39節點系統

算例1在本算例中設置負荷8為戴維南等值節點，負荷8處的負荷事件視為負荷側擾動，負荷21處的負荷事件視為系統內部擾動。設置仿真時長為8 s，負荷8處設置負荷斜坡增長，增長幅度為60%，系統其他負荷保持不變。由暫態仿真程序計算得到每0.2 s內20組電壓、電流仿真值，以每20組仿真數值為一組，應用算法得到一組戴維南等值參數值。圖3為該算例仿真結果圖。

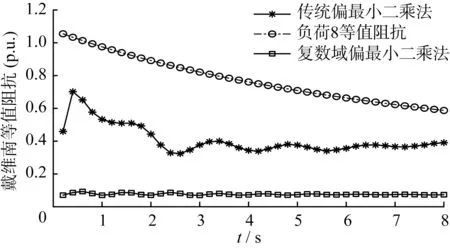
圖3 戴維南等值參數仿真結果

由圖3可知，在等值系統中僅有較明顯的外部擾動時，傳統偏最小二乘法和復數域偏最小二乘法均能計算出相對穩定的戴維南等值參數，但復數域偏最小二乘法得到的戴維南等值參數更加準確。

圖4為本文算法與傳統偏最小二乘法得到的戴維南等值參數標準差對比圖。

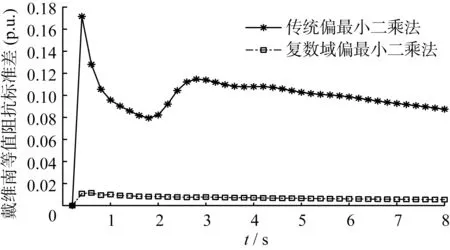
圖4 戴維南等值參數標準差結果

由圖4可知，傳統偏最小二乘法的戴維南等值阻抗標準差隨時間變化較大，標準差大多在0.08～0.12之間上下波動，而復數域偏最小二乘法的標準差在0.01上下浮動。可見傳統偏最小二乘法的等值阻抗標準差是復數域偏最小二乘法的8～12倍。表明在兩種算法都能得到較穩定的戴維南等值參數時，復數域偏最小二乘法跟蹤得到的戴維南等值參數更加穩定。

算例2在本算例中設置的等值節點同算例1中的相同，設置仿真時長為8 s。負荷8處設置負荷斜坡增長，增長幅度為40%，系統其他負荷保持不變。運用不同的分組計算一組戴維南等值參數。圖5給出了不同分組計算下的仿真結果對比圖。

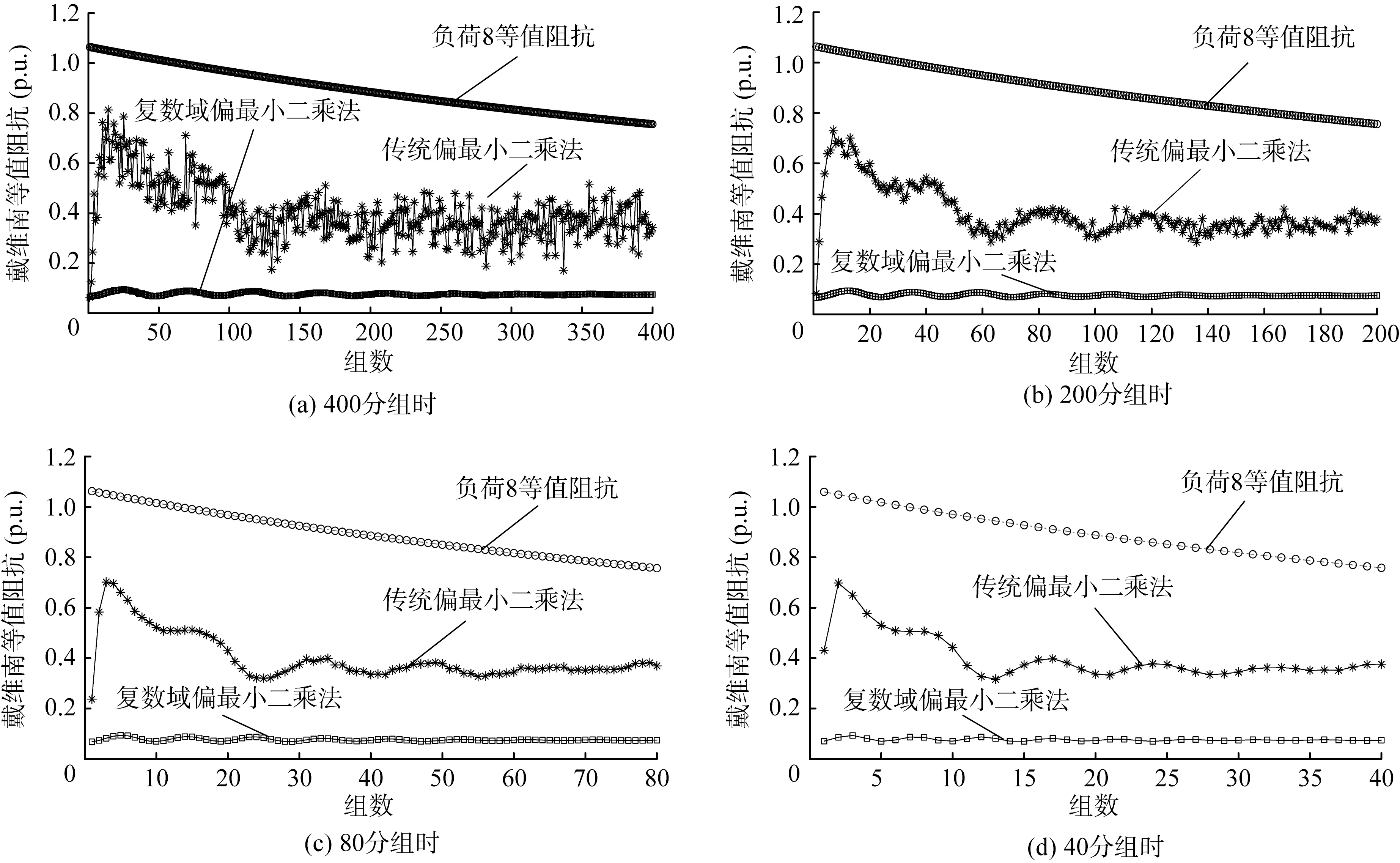
圖5 不同分組情況的戴維南等值參數仿真結果

由圖5可知，傳統偏最小二乘法仿真得出的戴維南等值參數隨著分組數的減少（即每次迭代的仿真數據越多）而逐漸穩定，振蕩情況改善越好，得到的數值越準確。傳統偏最小二乘法受數據量的影響較大，不同數據分組情況對算法的穩定性影響不一。復數域偏最小二乘法在不同分組情況下的仿真數據波動情況基本變化不大，在0.1值左右波動，數據振蕩較小。仿真結果表明，本文算法在不同分組情況下均能得到相對準確穩定的戴維南等值參數數值，每次迭代所用數據量對算法的穩定性影響較小。

算例3在本算例中設置負荷21為戴維南等值節點，負荷21處的負荷事件視為負荷側擾動，負荷27處的負荷事件視為系統內部擾動。設置仿真總時長為10 s。負荷事件設置為：0～4 s，負荷21斜坡增長5%，其余負荷保持不變；4～8 s，負荷21斜坡增長20%，同時負荷27斜坡增長80%，其余負荷保持不變；8～10 s，負荷21斜坡增長20%，同時負荷27斜坡增長20%，其余負荷保持不變。圖6為該算例仿真時長內的戴維南等值參數仿真結果。

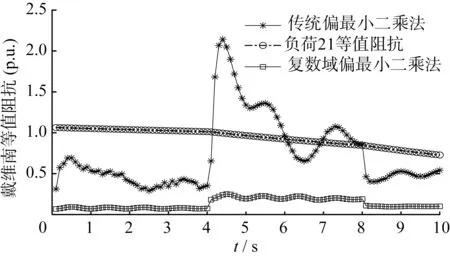
圖6 傳統偏最小二乘法與復數偏最小二乘法結果對比

由圖6可知，0～4 s時，等值系統僅有外部較小擾動時，傳統偏最小二乘法得到的等值阻抗值在0.3～0.8之間波動，仿真結果發生一定的波動，而復數域偏最小二乘法的仿真結果比較穩定準確。在4～8 s時，等值系統在等值系統側發生的擾動比負荷側明顯大時，等值系統內部擾動占主導，傳統偏最小二乘法仿真得到的戴維南等值阻抗值在負荷阻抗值上下波動，最大值超2 p.u.，嚴重偏離正確的戴維南等值阻抗值范圍，有明顯等值參數漂移現象，傳統算法在此情況下失效；而本文算法得到的戴維南等值參數在正常范圍內且數值波動較小，能夠準確地跟蹤戴維南等值阻抗值。在8～10 s內，負荷側擾動和系統側擾動大小一樣，傳統偏最小二乘法計算的等值參數有一定的誤差和波動，而本文算法能夠正確地跟蹤系統的戴維南等值阻抗。

算例4設置負荷27為戴維南等值節點，負荷27處的負荷事件視為負荷側擾動。設置仿真總時長為30 s。擾動設置為：0～30 s，負荷27斜坡增長30%，其余負荷保持不變；1 s時，母線9處發生三相短路故障，故障電抗設為10Ω；1.1 s時，切除三相短路故障。圖7為仿真時間內存在短路故障前后的戴維南等值參數仿真結果。

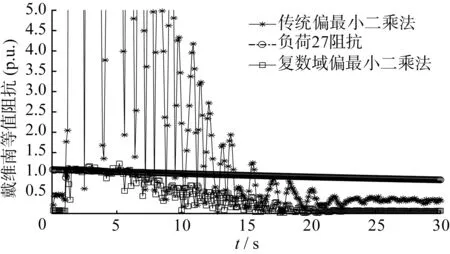
圖7 短路故障前后戴維南等值參數仿真圖

由圖7可知，1 s之前系統僅發生合適的負荷側擾動，等值阻抗曲線平穩；1 s時發生三相短路故障，傳統偏最小二乘法得到的仿真結果振蕩明顯，其值遠偏離了等值阻抗正常波動范圍，而復數域偏最小二乘法的曲線雖然有一定波動，但在切除故障后等值參數很快恢復在正常值內。相比傳統方法，本文算法能夠更快地跟蹤到戴維南等值參數，并且能保持等值參數的正確性和準確性。

4 結 語

本文提出了一種基于復數域偏最小二乘法的戴維南等值參數計算方法，改善了參數漂移問題。相比傳統偏最小二乘法，本文算法簡化了數學模型，用更少的測量變量得到更為準確的參數辨識結果。在IEEE 39系統下的仿真結果表明了該算法在等值系統多種擾動類型下的準確性和穩定性。